MIBS-64 算法的三子集中间相遇攻击*

2022-03-10许星霖李艳俊欧海文孙启龙

密码学报 2022年1期

关键词：明文密文复杂度

许星霖, 李艳俊, 欧海文, 孙启龙

1. 北京电子科技学院, 北京 100070

2. 密码科学技术国家重点实验室, 北京 100878

3. 中国电子科技集团公司第十五研究所, 北京 100083

1 引言

近年来, 为满足RFID (radio frequency identification)、智能卡、无线传感器等资源受限环境下的安全需求,轻量级密码倍受学术届的关注. 许多密码学者提出一系列轻量级分组密码算法,如PRESENT[1]、LED[2]、LBlock[3]、PRINT-cipher[4]、KLEIN[5]和SIMON[6]等.

MIBS[7]是由Izadi 等在CANS 2009 上提出一个轻量级分组密码算法. 针对该算法的现有分析结果包括Bay 等提出的线性分析[8]和差分分析[8]、Liu 等提出的中间相遇攻击[9]、Yu 等提出的积分分析[10]等. 目前对于MIBS-64 最好的分析结果是14 轮差分分析[8], 数据复杂度为240个选择明文, 时间复杂度为237.2, 成功概率为50.15%; 对于MIBS-80 最好的分析结果是18 轮线性分析[8], 数据复杂度为260.98个已知明文, 时间复杂度为276.13, 成功概率为72.14%. 虽然差分分析和线性分析的轮数较高, 但是成功率相对中间相遇攻击偏低.

中间相遇攻击是1977 年Diffie 和Hellman 为分析DES 算法安全性提出的一种攻击方法. 近年来,中间相遇攻击广泛发展, 已经应用于很多密码算法, 如ARIA[11]、AES[12]、TWINE[13]、Camellia[14]等. 基于传统的中间相遇攻击, 产生了很多改进后的攻击方法, 例如, 三子集中间相遇攻击. 三子集中间相遇攻击由Bogdanov 等[15]在轻量级分组密码KTANTAN 的安全性分析中首次提出, 通过使用部分匹配技术和优化密钥子集合的选取, 增加了传统中间相遇攻击可分析的轮数. 三子集中间相遇攻击有效地拓宽了中间相遇攻击在分组密码安全性分析中的应用. 其他应用可参见Sasaki 等[16]对XTEA 算法的安全性分析. 目前, 三子集中间相遇攻击有较为完备的自动化搜索方法, 例如Sasaki[17]在IWSEC 2018 上提出使用ILP 对GIFT 算法进行三子集中间相遇攻击自动化搜索, Bao 等[18]在Eurocrypt 2021 上提出对AES-like 哈希的中间相遇原像攻击的自动搜索, 2021 年Dong 等[19]提出着重于密钥恢复和碰撞分析的中间相遇攻击.

本文针对MIBS-64 算法的密钥编排特点, 使用三子集技术、剪切–拼接技术和MIBS 的等价结构, 首次对MIBS-64 进行了11 轮的中间相遇攻击, 数据复杂度为247, 存储复杂度为24764-bit, 时间复杂度为262.25次11 轮加密.

本文结构如下: 第2 节简单介绍MIBS 算法和所使用的符号. 第3 节介绍三子集中间相遇攻击.第4 节给出MIBS-64 的密钥编排性质、MIBS-64 的11 轮的攻击与复杂度分析. 第5 节为结论及工作展望.

2 预备知识

2.1 MIBS 算法简介

MIBS 是一个轻量级分组密码算法, 其结构为Feistel 结构. MIBS 密码的分组长度为64 比特, 支持64 和80 比特的密钥长度, 分别记为MIBS-64 和MIBS-80, 迭代轮数为32 轮. MIBS 中所有迭代操作都是基于半字节的, 也就是基于4 比特进行操作. MIBS 的轮函数包括异或子密钥, S 盒(4×4 比特) 层和一个线性层P(分支数为5), 此处线性层是设计文档中线性混淆和半字节置换的复合. MIBS 加密结构及轮函数结构见图1 及图2.

图1 MIBS 算法一轮加密结构Figure 1 One round structure of MIBS

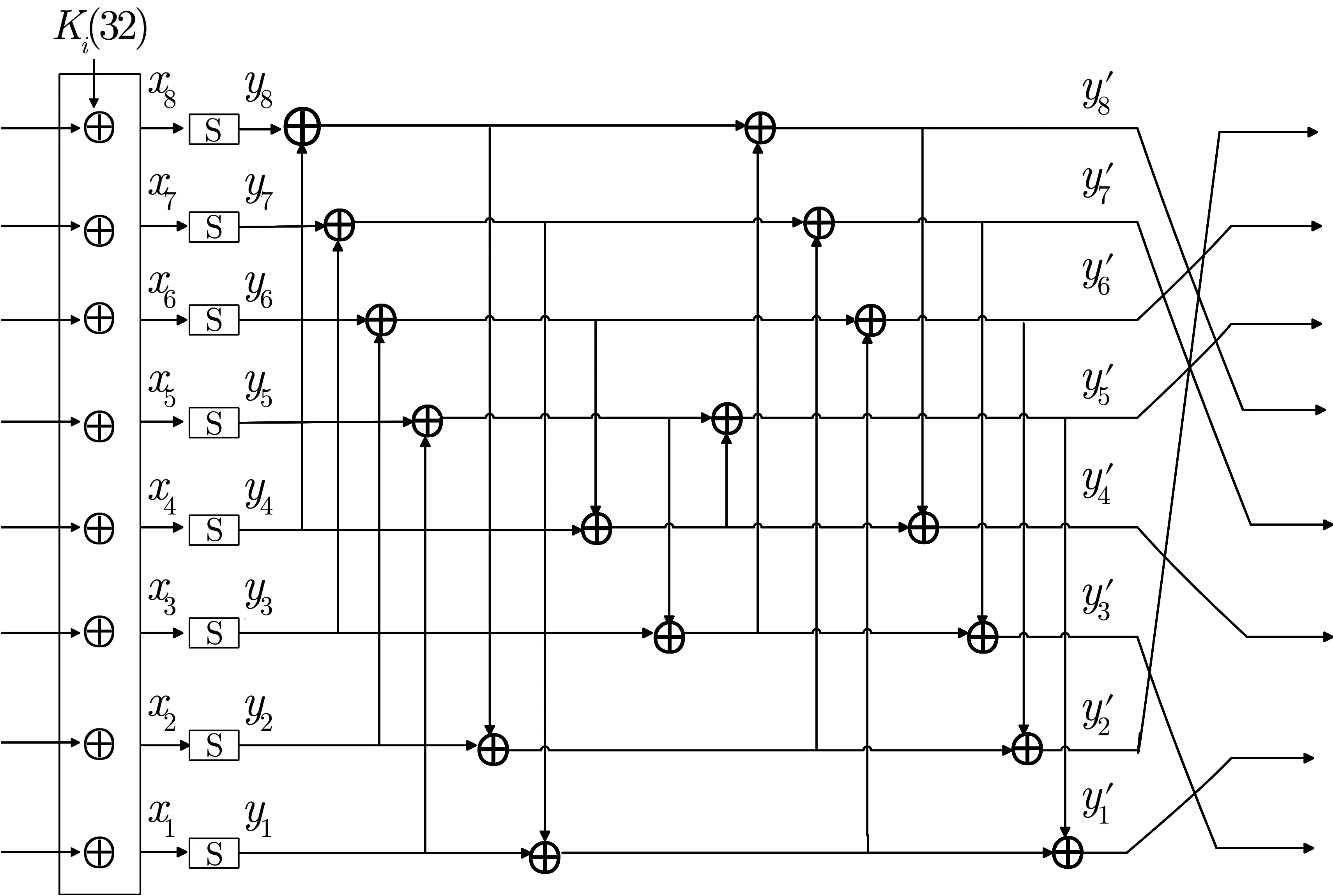
图2 MIBS 算法轮函数结构Figure 2 Round function of MIBS

在攻击中, 线性层P很重要, 令(y1,y2,··· ,y8) 为线性层P的输入, 则输出(y′1,y′2,··· ,y′8) 可以如下表示:

令(y1,y2,··· ,y8) 为线性层P的输出, 则输入(y′1,y′2,··· ,y′8) 线性层P的逆P-1可以如下表示:

MIBS 的密钥编排采用了与PRESENT 的密钥编排相同的设计原则. MIBS-64 密钥编排中, 通过64比特主密钥K:(k63,k62,··· ,k0) 生成轮密钥ki, 其中0≤i ≤31. 若将密钥编排算法中第i轮的密钥状态表示为statei, 则密钥编排算法的轮函数可以表示成如下的形式:

2.2 符号说明

首先说明本文中使用的符号. 明文记为P= (X1,X0), 其中Xi= (x8,x7,··· ,x1),i= 0,1, 其中xj(j=1,2,··· ,8) 为4 bit 的半字节, 本文中出现的其他符号含义如下:

3 三子集中间相遇攻击简介

3.1 三子集中间相遇攻击

三子集中间相遇攻击是中间相遇攻击的一种改进方法, 通过放宽选取密钥子集合的严格要求, 使得攻击的应用范围变广. 与传统中间相遇攻击将密钥空间划分为2 个完全独立的子密钥集合不同, 三子集中间相遇攻击将密钥空间划分为3 个子密钥集合.

如图3 所示, 令密钥长度为l,K=kl-1···k1k0为初始密钥. 定义K1={ki|应用于φ1,α的密钥比特集合},K2={ki| 应用于φR-β+1,R的密钥比特集合},A0=K1∩K2为加密过程中φ1,α与φR-β+1,R共有的密钥比特集合, 则A1=K1K1∩K2与A2=K2K1∩K2为仅在φ1,α与φR-β+1,R中使用的密钥比特集合, 并有K=K1∪K2.

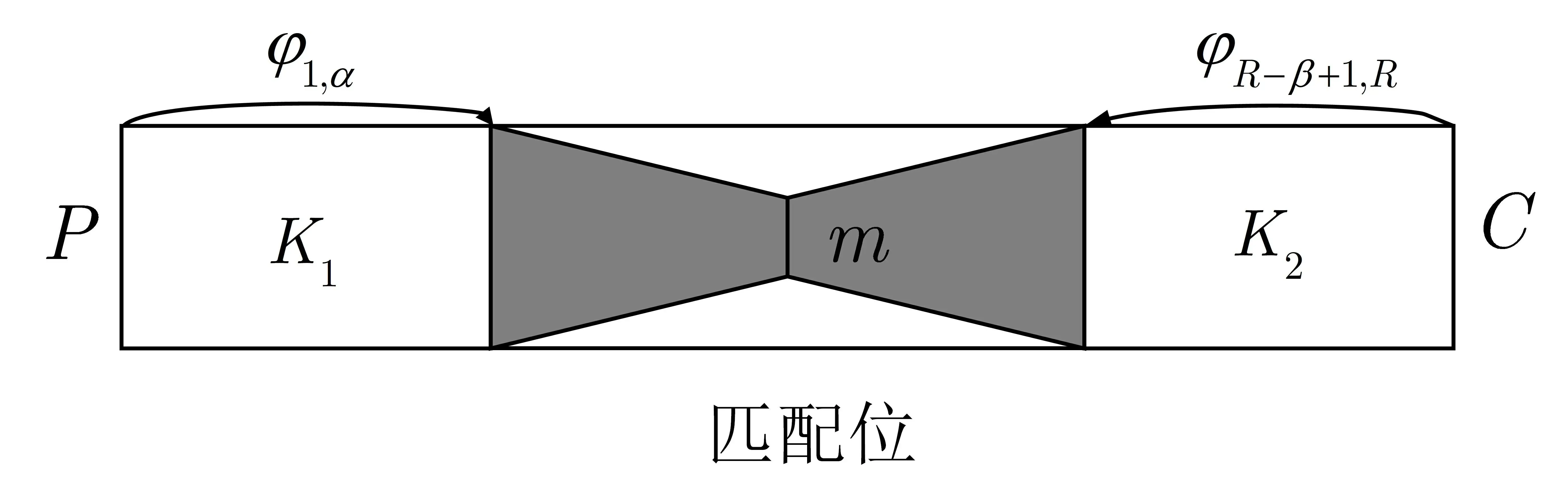
图3 三子集中间相遇结构Figure 3 3-subset meet-in-the-middle structure attack

三子集中间相遇攻击的过程包括2 个步骤: 首先建立三子集中间相遇结构, 并利用该结构过滤部分错误密钥, 减小密钥空间; 然后通过进一步的密钥筛选寻找正确密钥[20].

首先建立三子集中间相遇结构.

(P,C) 为一个明密文对, 猜测A0中密钥的所有可能值.

(1) 猜测A1中密钥的所有可能值, 计算v=φ1,α(P), 将其结果存入表中;

(2) 猜测A2中密钥的所有可能值, 计算u=(C);

(3) 确定进行中间匹配的轮数, 对v与u分别进行加密与解密运算, 得到匹配轮数处对应的加密结果v′与解密结果u′的m(1≤m ≤b) 个比特, 并对m个比特值进行匹配, 若m个比特值不完全相同, 则认为是错误密钥. 该步对密钥的筛选概率为2-m, 即经过该步筛选后剩余密钥数为2l-m. 该步的计算复杂度为2|A0|(2|A1|+2|A2|).

接下来, 进一步对剩余所有密钥进行筛选.

穷举搜索剩余的所有密钥候选值, 利用明密文对(P,C) 计算中间匹配轮数处v′与u′的值, 并对其全部b比特值进行匹配, 若b比特值不完全相同, 则认为是错误密钥. 一次匹配可删除2b个错误密钥. 对剩余的2l-m-b个可能密钥候选值重复该过程, 直到得出唯一的正确密钥.

该步的计算复杂度为2l-m+2l-m-b+2l-m-2b+···.

完整三子集中间相遇攻击的计算复杂度为2|A0|(2|A1|+2|A2|)+(2l-m+2l-m-b+2l-m-2b+···).

3.2 剪切-拼接技术

剪切–拼接技术(splice-and-cut technique) 是Aoki 和Sasaki[21]在对SHA-0 和SHA-1 进行中间相遇攻击时提出的. 剪切–拼接技术可以使得进行中间相遇攻击时不再局限于以明文或密文为起点, 此时可以随机选取某一轮的中间状态, 如果这个中间状态选择在前端的时候, 需要猜测中间状态解密到明文的所有所需密钥, 从而解密得到相应的明文, 进而通过加密机得到密文, 然后进行中间相遇攻击. 同理, 中间状态选择尾端时, 也要猜测中间状态加密到密文的所有所需密钥, 从而加密得到相应的密文, 进而通过解密机得到明文, 然后进行中间相遇攻击. 在使用剪切–拼接技术时, 需要建立明文–密文对的索引表, 以便在攻击中可以找到密文对应的明文, 将整个过程连接起来. 剪切–拼接中间相遇攻击结构如图4 所示.

图4 剪切–拼接技术Figure 4 Splice-and-cut technique

剪切–拼接技术通过建立明文和密文之间的查找表(LOOKUP 表) 将明密文连接起来, 通过猜测某一轮的中间状态h,猜测从h加密到密文C中所需的密钥H1,从h加密得到密文C,得到密文C之后,可以通过LOOKUP 表查找得到相对应的明文P, 猜测密钥H2, 对明文P进行加密, 得到v; 猜测从h解密到中间状态u中所需的密钥G,从h解密得到中间状态u,对于中间相遇攻击则有H2(LOOKUP(H1(h)))=G-1(h).

定义K1={ki|应用于H1与H2的密钥比特集合},K2={ki|应用于G的密钥比特集合},A0=K1∩K2,A1=K1K1∩K2,A2=K2K1∩K2, 并有K=K1∪K2.

剪切–拼接三子集中间相遇攻击的步骤如下[22]:

对A0的每种猜测值:

(1) 猜测A1中密钥的所有可能值, 计算v=H2(LOOKUP(H1(h))), 将其结果存入表T1中;

(2) 猜测A2中密钥的所有可能值, 计算u=G-1(h);

(3) 确定进行中间匹配的轮数, 对v与u分别进行加密与解密运算, 得到匹配轮数处对应的加密结果v′与解密结果u′的m(1≤m ≤b) 个比特, 并对m个比特值进行匹配, 若m个比特值不完全相同, 则认为是错误密钥. 该步对密钥的筛选概率为2-m, 即经过该步筛选后剩余密钥数为2l-m, 再进一步对剩余所有密钥进行筛选.

剪切–拼接三子集中间相遇攻击的数据复杂度为H1中猜测密钥的个数, 存储复杂度为LOOKUP 表与表T1之和. 普通的中间相遇攻击仅仅需要知道明密文对即可, 而剪切–拼接三子集中间相遇攻击则为选择明密文攻击.

4 MIBS 的三子集中间相遇攻击

MIBS-64 密钥编排算法中使用了循环移位、S 盒查询、轮常数加等变换, 相邻两轮之间的32 比特密钥有17 比特重复或等价, 基于这个性质可以对MIBS-64 进行多轮攻击. 本节将首先介绍MIBS-64 的密钥性质.

4.1 MIBS-64 的密钥性质

根据MIBS-64 密钥编排算法, 第1 轮至第11 轮之间的密钥存在部分重复和等价关系, 本文主要使用下述密钥编排性质.

引理1 根据MIBS-64 密钥编排算法,k11,[10,9,8,7]可由k2,[3,2,1,0]查S 盒得到, 同理,k11,[32,31],k11,[30,29,28,27],k11,[26,25,24,23]可由主密钥相应比特查询S 盒得到;第1、2 轮共实际使用密钥32+15=47比特; 第10、11 轮另存在7 比特额外密钥.

证明: 根据密钥编排算法state1经过循环右移15 bit、S 盒和异或轮常量即可得到state2, 考虑到S 盒以及异或轮常量不会引入未知量, 则可以通过上述性质详细刻画state1与state2之间的关系. 因为Ki=, 则可以通过state1与state2之间的关系得出K1与K2之间的关系. 迭代上述过程即可得到K1:K11之间的密钥相关性, 具体性质如表1 所示.

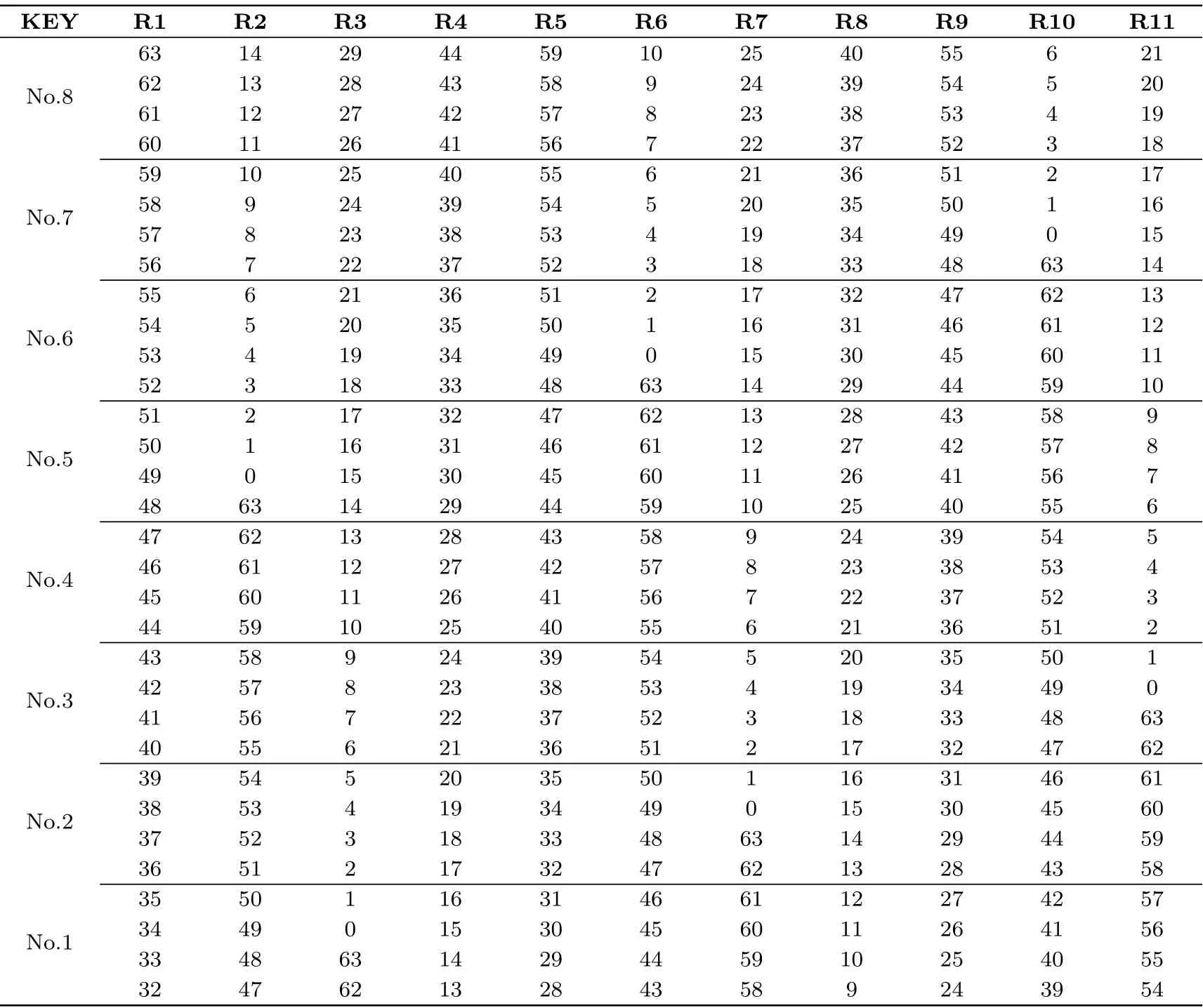
表1 轮密钥之间的关系Table 1 Relationship between round keys

三子集中间相遇攻击利用MIBS 一些密钥比特在连续的多轮加密过程中未被使用的特点. 所以为了建立MIBS 的三子集中间相遇结构, 首先推导各轮加密使用的轮密钥. 根据MIBS 密钥生成策略得到的各轮轮密钥的使用情况如图表1 所示. 可以看出, MIBS 中第1、2 轮密钥与第10、11 轮密钥存在较多重复比特.

4.2 MIBS 算法的一种等价结构

文献[23] 利用线性变换的性质给出了轮函数为SPN 结构的Feistel 密码的3 个等价结构, 利用不同结构对算法实施攻击时可以得到不同的改进效果. 同样地, 记MIBS 算法加密过程中轮密钥加操作为K,非线性代替变换为S, 线性变换为T, 则四轮MIBS 算法的加密结构可描述为图5 中的左图. 根据MIBS算法加密结构中线性变换的性质, 可以相应地给出四轮MIBS 的一个等价加密结构为图5 中的右图[9].

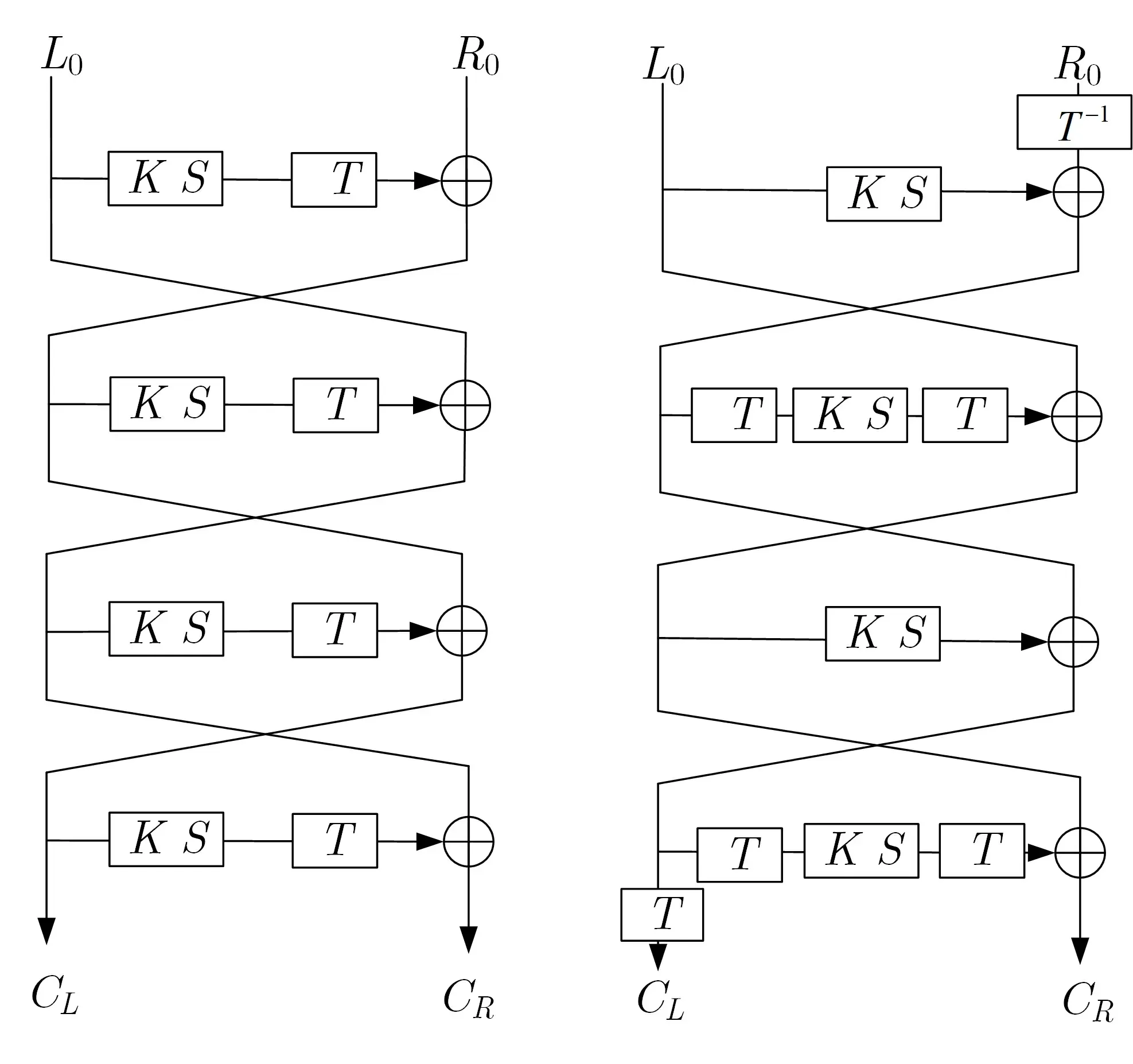
图5 4 轮MIBS 及其等价结构Figure 5 4-round MIBS and its equivalent structure

4.3 11 轮MIBS-64 的三子集中间相遇攻击

观察MIBS-64 各轮轮密钥可有如下发现.

从第1、2、10、11 轮的轮密钥涉及的密钥比特集合为{k0,k1,··· ,k21,k32,··· ,k63}, 未使用实际密钥的集合为{k22,k23,··· ,k31}. 从第7 轮至第9 轮的轮密钥涉及的密钥比特集合为{k0,k1,··· ,k55,k58,··· ,k63}, 未使用实际密钥的集合为{k56,k57}.

根据第3 节中对三子集中间相遇攻击和剪切–拼接技术的介绍, 选取H1为第10、11 轮密钥,H2为第1、2 轮密钥,G为第7 轮至第9 轮密钥, 即可将实际密钥空间划分为3 个子集合A0、A1和A2, 划分方式如下:

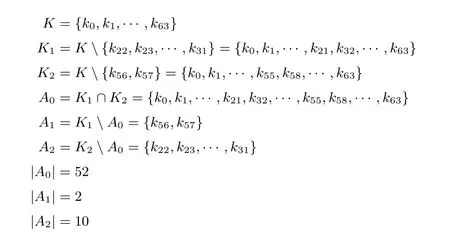
利用这些参数和图6 的MIBS 算法8 轮的等价加密结构即可得到11 轮MIBS-64 的三子集中间相遇结构, 并对密钥进行初步筛选. 具体过程如下:

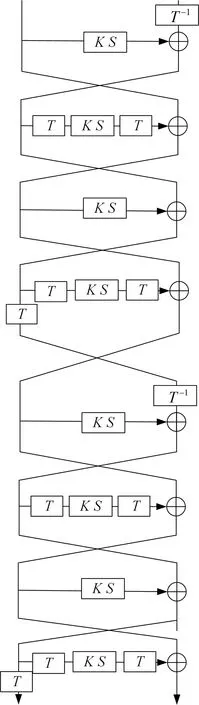
图6 基于MIBS 的8 轮等价结构Figure 6 8-round equivalent structure based on MIBS

A0有252种可能, 假设第10 轮的输入数据为h:

(1) 猜测A1中密钥的所有22种可能值, 计算v=φ1,2°LOOKUP°φ10,11(h), 将v存储进表T1;

(2) 猜测A2中密钥的所有210种可能值, 计算u=(h);

(3) 选择第5 轮输入为中间匹配轮数, 得到第5 轮输入处的v′与u′, 具体推导过程如表2 所示, 其中将4 bit 视为一个块, 对于正向(反向) 而言, 0 代表不受A2(A1) 的影响, 1 代表受到A2(A1) 的影响, 可以看到仅第5 轮右支输入的第5 个块输入不受影响独立密钥A2、A1影响. 对v′与u′均不受独立密钥影响的4 个比特值进行匹配, 若4 个比特值不完全相同, 则认为是错误密钥, 筛选概率为2-4.

表2 中间匹配过程Table 2 Intermediate matching process

该步的计算复杂度为252(22+210)=262.

接下来, 穷举搜索剩余2l-m= 260个密钥候选值, 利用明密文对(P,C) 重新计算v′与u′的值, 并对其64 bit 值进行匹配, 若64 bit 值不完全相同, 则认为是错误密钥, 该步的筛选概率为2-64. 重复该步骤, 直到得到满足v′=u′的唯一正确密钥.

该步的计算复杂度为2l-m+2l-m-b+2l-m-2b+···=260+2-4+···≈260. 观察该式可发现, 对MIBS-64 只需要一步筛选即可期待淘汰所有错误密钥, 得到唯一的正确密钥.

4.4 11 轮MIBS-64 的复杂度分析

根据第3 节中对三子集中间相遇攻击复杂度计算的结果, 恢复11 轮MIBS-64 实际全部64 bit 密钥信息的计算复杂度为2|A0|(2|A1|+2|A2|)+(2l-m+2l-m-b+2l-m-2b+···)=252(22+210)+260+2-4≈262.25, 数据复杂度为247, 存储复杂度为24764-bit.

5 结束语

本文对分组密码算法MIBS-64 进行了三子集中间相遇攻击, 11 轮的密钥恢复攻击数据复杂度为247,时间复杂度为262.25, 存储复杂度为24764-bit. 表3 给出了一些针对MIBS-64 的攻击结果, 同现有的攻击成功率为100% 的密码分析方法相比, 使用三子集中间相遇攻击增加了攻击轮数, 且具有较低的数据复杂度. 本攻击结果适用于MIBS-64, 类似地可以推广至MIBS-80. 由分析结果可见, 轮密钥之间的关系对算法安全性有重要影响. 若能使用自动化搜索工具, 则可能搜索出更优的密钥子集合的划分, 从而改进现有分析效果, 这也是我们下一步的工作.