不可否认协议分析的扩展ZQZ 逻辑方法*

韩志耕, 石青山, 杨 鹏, 陈 耿, 范远哲

1. 南京审计大学 信息工程学院, 南京 211815

2. 江苏省审计信息工程重点实验室(南京审计大学), 南京 211815

1 引言

2020 年受新冠疫情“黑天鹅” 事件的影响, 人们的工作方式和生活习惯悄然发生了改变, 在线办公、在线购物、在线教育和在线医疗等需求显著增加. 伴随着线下活动大规模向线上迁移, 网络欺诈也随之泛滥[1]. 据360 猎网平台统计数据显示, 疫情期间共收到网络欺诈举报3243 例, 比上一年同期增长了47%.网络欺诈在特征上表现为网络行为真实, 而网络主体不诚实, 对其进行取证需要借助不可否认服务进行.该类服务通过生成、交换和管理一系列与网络行为有关的密码学证据, 为溯源网络欺诈提供依据, 在物联网安全[2]、合同签名[3]、签收邮件[4,5]等领域应用广泛. 不可否认服务的实现依赖于不可否认协议. 不可否认协议逻辑复杂, 细小的逻辑缺陷都会导致不可否认服务失效, 使得相应的网络欺诈无法溯源.

逻辑正确的不可否认协议通常需要满足存活性、不可否认性、公平性和时限性[6,7]. 形式化分析是验证该类协议逻辑是否正确的常用手段. 以ZG 协议[8]为例, 为验证其逻辑是否正确: (1) 在逻辑推理方面,Zhou 等人使用SVO 逻辑分析过其不可否认性[9]; 黎波涛等人使用改进的SVO 逻辑分析过其时限性[10];基于改进的SVO 逻辑, 韩志耕等人分析过该协议多方多消息变体的不可否认性、公平性和时限性[11,12];苑博奥等人分析过多方单消息变体[13]和带区块链的多方单消息变体[14]的不可否认性、公平性和时限性; 周典萃等人使用类Kailar 逻辑(简称ZQZ 逻辑) 分析过ZG 协议的不可否认性和公平性[15]; Liu等人使用改进的ZQZ 逻辑分析过ZG 协议及其变体的不可否认性、公平性和时限性[16]. (2) 在模型检测方面, 黎波涛等人使用有色Petri 网分析过其公平性[17]; Kremer 等人[18]首次利用基于博弈论的交替转换逻辑ATL 和模型检测工具MOCHA 分析过该协议多方单消息乐观变体的公平性; 文静华等人使用ATL 和MOCHA 分析过该协议及其两方乐观变体的保密性、不可否认性、公平性及时限性[19,20]; 汪学明等人[21]使用MOCHA 分析过该协议多方单消息变体的不可否认性和抗合谋性. (3) 在定理证明方面, 沈海峰等人利用串空间结点标号的递归公平交换协议分析方法分析过该协议的公平性[22]; 王涛等人利用扩展的串空间模型分析过其乐观变体的公平性[23]; Li 等人利用串空间模型分析过其多方单消息变体的公平性[24]; 姚萌萌等人利用扩展的串空间理论分析过该协议基于区块链的多方变体的不可否认性、公平性和时限性[25]; Bella 等人使用Paulson 归纳法分析过该协议的不可否认性[26]. (4) 在进程代数方面,Schneider 利用CSP 分析过该协议的不可否认性和公平性[27]; 韩志耕等人利用增广CSP 分析过该协议[28]及其多方单消息变体[29]的不可否认性、公平性和时限性; 李援等人利用扩展SPI 演算分析过其不可否认性[30].

逻辑推理类方法抽象程度高, 但描述能力弱; 模型检测类方法容易出现状态爆炸, 在主体数量加大时会因状态过多而造成无法分析; 定理证明类方法可以证明协议逻辑的正确性, 但对不能完成证明的协议无法指出其存在的安全缺陷, 对协议设计的指导能力有限; 进程代数类方法对发现协议攻击非常有效, 但不可否认侧重于防范实体欺诈而非网络攻击. 这四类方法各有优势, 但共同点是它们中的绝大多数方法仅能对不可否认协议的部分性质进行建模与分析、证明或证伪协议逻辑的局部正确性. 以ZQZ 逻辑[15]为例,该方法虽然目前被关注较少, 但其具备的无状态爆炸、支持密文处理、初始假设形式化, 尤其是其所基于的面向责任分析与不可否认协议所侧重的欺诈溯源高度契合, 使其应用于不可否认协议的分析前景广阔.该逻辑的不足是时间描述能力弱, 无法分析协议的时限性. 鉴于当前趋势是综合利用多种手段, 取长补短,以期发现更多的协议缺陷, 达到更好的分析效果. 借助于时间表达式可以描述协议事件的发生时间、刻画事件间的时序关系, 已被广泛应用于协议时限性建模与分析[10,12,14,28]的事实, 本文通过向ZQZ 逻辑添加时间表达式, 提出了一种适用于不可否认协议建模与分析的扩展ZQZ 逻辑方法. 与Liu 等人[16]的工作不同, 扩展ZQZ 逻辑方法在建模与分析时将协议性质按照是否与时间相关做了区别对待, 仅在分析时间相关的性质(如时限性) 时才涉及到对事件发生时间及约束关系的处理, 极大降低了协议分析的复杂度.

本文主要贡献在于:

(1) 给出了扩展ZQZ 逻辑方法框架, 包括推理规则和安全性质模型. 与原逻辑相比, 扩展后的逻辑除了增加时限性分析功能外, 还提高了对密文信息的处理能力.

(2) 以ZG 和KPB 这两个局部逻辑正确性已知的不可否认协议为实验对象, 系统性地介绍了使用扩展ZQZ 逻辑对不可否认协议的分析步骤, 通过实验结果与既有事实的符合性, 从逆向工程角度验证了该方法的功能有效性.

(3) 利用该方法对YLL 这个逻辑正确性尚在讨论的、基于区块链的公平多方不可否认协议进行探索性分析, 发现其存在一个尚未公开的时限性异常, 并给出了对应的协议改进方案.

(4) 将扩展ZQZ 逻辑方法与另外12 种常用的不可否认协议分析方法从理论基础、性质分析、状态爆炸、自动化程度、抽象程度、密文处理这6 个维度作了功能比较.

论文其余部分组织如下: 第2 节给出了扩展ZQZ 逻辑方法; 第3 节和第4 节利用该逻辑分别对ZG 和KPB 进行了建模与分析, 以逆向验证新逻辑的功能有效性; 第5 节利用该逻辑对YLL 协议的时限性逻辑进行了探索分析, 发现该协议存在一个尚未公开的时限性异常; 第6 节将扩展ZQZ 逻辑与现有常用的分析方法进行了比较; 最后第7 节总结全文.

2 扩展ZQZ 逻辑

2.1 ZQZ 逻辑介绍

ZQZ 逻辑是周典萃等人[15]提出的一种用于分析电子商务协议的新工具, 其目的是解决Kailar 逻辑在电子商务协议分析方面的能力不足. 电子商务协议必须遵循可追究性(迫使交易双方对自己的行为负责) 和公平性(保证电子货物获取的对等性), 而Kailar 逻辑只能分析电子商务协议的可追究性, 其缺陷[31]包括: (1) 不能分析协议的公平性; (2) 列举初始化假设是非形式化的, 假设的不当会导致协议分析的失败; (3) 无法理解包含签过名的密文的协议语句. ZQZ 逻辑本质上是一种类Kailar 逻辑, 它使用拥有集合来记录协议实体的信息状态, 使用推理规则来推演协议事件间的关联. 每个主体在协议运行前拥有一个初始拥有集合, 之后该集合随着协议语句的执行不断更新, 在协议运行结束时每个主体将拥有最终拥有集合. 该逻辑方法通过判断发方不可否认证据(proof-of-origin, POO) 是否属于收方最终拥有集合来验证协议是否满足发方可追究性、通过判断收方不可否认证据(proof-of-receipt, POR) 是否属于发方最终拥有集合来验证协议是否满足收方可追究性; 通过验证协议的执行在任何一步异常终止时, POO 属于收方的拥有集合是否当且仅当POR 属于发方的拥有集合来验证协议的公平性; 通过增加密文理解规则, 来分析包含签过名的加密公式的消息; 此外, 初始拥有集合的设置仅依赖环境而非人为引入的初始化假设, 避免了假设不当造成的协议分析失败.

不可否认协议对时间敏感, ZQZ 逻辑无法描述协议事件的发生时间, 无法刻画协议事件间的时序关系. 下面对ZQZ 逻辑进行扩展, 以使其能够分析不可否认协议更多的性质.

2.2 标识及其含义

2.3 拥有集合更新

扩展ZQZ 逻辑仍采用原逻辑的拥有集合, 简介如下:

主体P的拥有集合是协议环境赋予P的信息、能证明的公式, 以及获得的信息集合. 协议运行前P的初始拥有集合记为O0P, 协议执行后P的拥有集合OP=OnP, 其中n为协议步数.OiP的更新策略为:

2.4 推理规则扩展

在介绍扩展ZQZ 逻辑的推理规则之前, 首先给出本文所使用的时间表达式.

定义1 (时间常元) 设Integer={0,1,2,···}∪{-1,-2,···},v是时间常元, 当v ∈Integer.

定义2 (时间变元)V是时间变元, 当V是一个变域为Integer 的变元.

定义3 (时间绑定表达式)V|TB 是时间绑定表达式, 当V是时间变元且TB⊆Integer.

定义4 (时间表达式) [T] 是时间表达式, 当T是时间绑定表达式.

规则R1 (1) 是对原ZQZ 逻辑签名规则的时间拓展, 规则R1(2) 是新引入的签名规则.

R2. 分解与合并规则

(1) 负责分解与合并规则: 若P证明Q在T时间对公式(x1,x2,··· ,xn) 或公式xi负责, 则可证明Q在T时间对公式xi或公式(x1,x2,··· ,xn) 负责. 即:

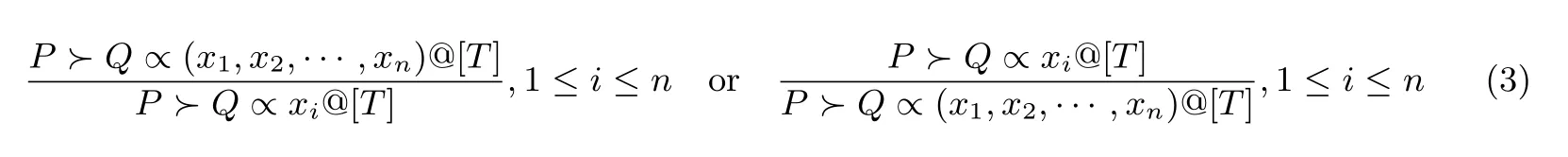
(2) 拥有分解与合并规则: 若P证明Q在T时间拥有公式(x1,x2,··· ,xn) 或公式xi, 则其能证明Q在T时间拥有公式xi或公式(x1,x2,··· ,xn). 即:

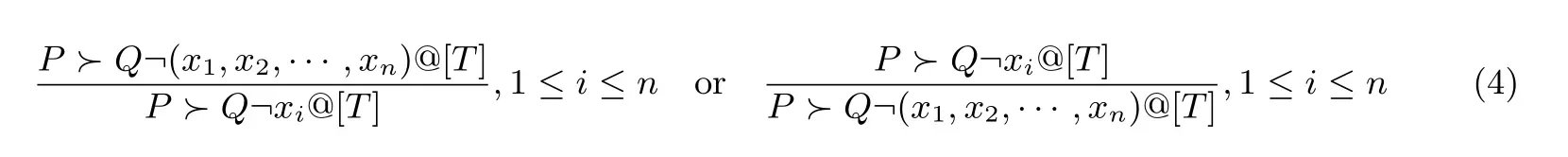
规则R2(1) 是对原ZQZ 逻辑连接规则的改进与时间拓展, 规则R2(2) 是新引入的规则.

R3. 密文理解规则

(1) 加密规则: 若P证明在T时间Q对{x}K负责, 且证明Q拥有对称密钥K, 则其能证明Q在T时间对x负责. 即:

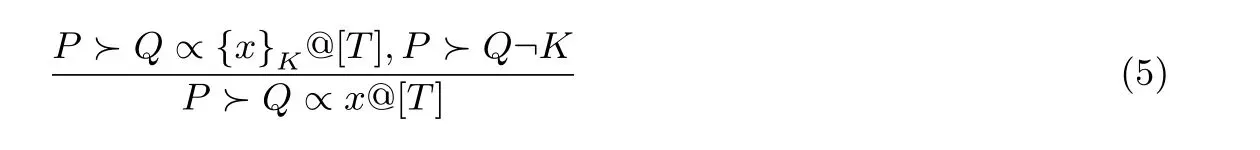
(2) 解密规则: 若P证明Q在Tx时间拥有密文{x}K, 且证明Q在Ty时间拥有对称密钥K, 则其能证明Q在max(Tx,Ty) 时间拥有x. 即:

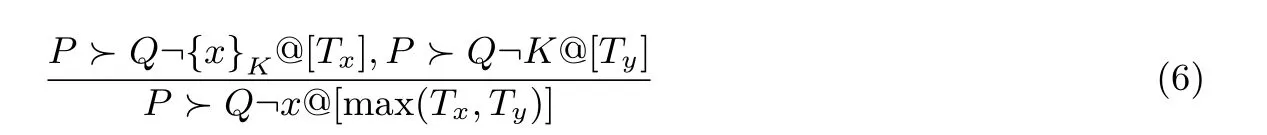
(3) 隐私规则: 若P证明Q在T时间拥有公钥KQ加密形成的密文{x}KQ, 且证明KQ能验证Q身份, 则其能证明Q在T时间拥有x. 即:

规则R3(1) 是对原ZQZ 逻辑密文理解规则的时间扩展, 规则R3(2) 和R3(3) 是新引入的密文理解规则.

R4. 拥有规则

这是对原ZQZ 逻辑拥有规则的改进. 若P拥有集合OiP中包含公式x, 那么Q能证明P拥有该x.即:

R5. 传递规则

这是对原ZQZ 逻辑传递规则的改进与时间拓展. 令TTP 向P和Q共享消息x, 若P能够证明TTP 在时间T对x负责, 那么它能够分别证明P在后继时间Tx、Q在后继时间Ty也必定拥有x. 即:

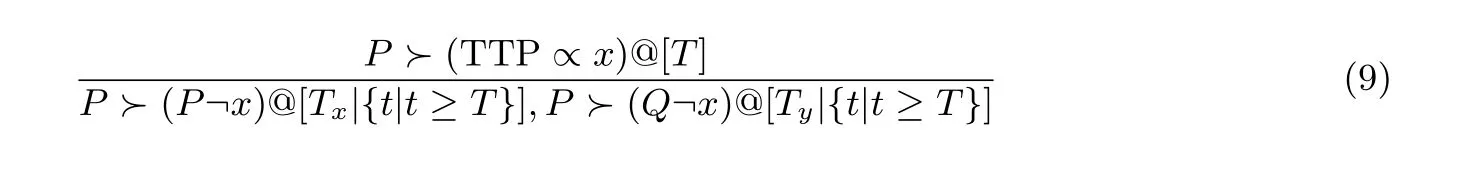
R6. 证书规则

这是对原电子证书规则的时间拓展. 若P能够证明电子证书机构CA 在时间T对公式(KQ,Q) 负责, 那么P能够证明在后续时间Tx可用KQ验证主体Q的身份(其中Trev为证书撤销时间). 即:

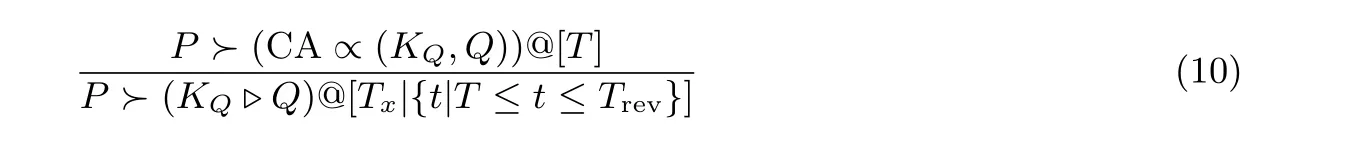
2.5 安全性质建模

扩展ZQZ 逻辑将存活性、不可否认性、公平性视为时间不相关性质, 将时限性视为时间相关性质. 前者在描述时无需引入时间信息.

令A是发方,B是收方,J是仲裁方, POO、POR 和M是数据, Pr 是密码协议,R是Pr 的一次成功运行实例.

定义5 (存活性) Pr 满足存活性, 若存在一个R有: (1)R之前:A持有M但不持有POR,B不持有POO 和M. (2)R之后:A持有POR,B持有POO 和M. 即:∃R,POR∈OA ∧POO∈OB.

定义8 (不可否认性) 若Pr 既满足发方不可否认性, 又满足收方不可否认性, 则Pr 满足不可否认性.

定义9 (公平性) Pr 满足公平性, 若对于任意的R有: (1)R之前:A持有M且A不持有POR,B不持有POO 和M. (2)R之后:A持有POR 且B持有M和POO, 或者A不持有POR 且B不持有POO 和M. (3) 如果A持有POR, 那么B持有M; 如果B持有POO 和M, 那么A持有M.

定义10 (可中断) 可中断是指协议语句在执行中可能会出现诸如未执行、未正确执行等异常情况. 如A →B:M就是可中断的, 因为非诚实的A可能会因私利而未按规定执行该语句.

定义11 (不可中断) 不可中断是指协议语句在执行中不可能出现诸如未执行、未正确执行等异常情况. 如B ↔TTP :M就是不可中断的, 因为诚实的TTP 总会在ftp 服务中发布M,B总会利用ftp 设法从TTP 处获取M.

公平性可形式化为, 对于Pr 的任意可中断语句i, 若POO∈iffPOR∈, 则Pr 满足公平性.

定义12 (发方时限性) Pr 满足发方时限性, 若对于Pr 的任意运行实例R都有: (1)R之前:A持有M但不持有POR. (2)R之后:A持有POR. (3) 若A在T时间发送了M, 则其一定可在未来ε(ε ≪+∞) 时长内持有POR. 即J ≻(A ∝M@[T],A¬POR@[Tx|{t|T ≤t ≤T+ε, ε ≪+∞}]).

定义13 (收方时限性) Pr 满足收方时限性, 若对于Pr 的任意运行实例R都有: (1)R之前:B不持有POO 和M. (2)R之后:B持有POO 和M. (3) 若B在T时间持有M, 则其一定在之前的ε(ε ≪+∞) 时长内持有POO. 即J ≻(B¬M@[T],B¬POO@[Ty|{t|T-ε ≤t ≤T, ε ≪+∞}]).

定义14 (时限性) 若Pr 既满足发方时限性, 又满足收方时限性, 则Pr 满足时限性.

3 ZG 协议分析

3.1 协议描述

ZG 协议[8]的交互步骤描述如下:

3.2 协议假设集

协议各方拥有CA为其生成的签名私钥与验证公钥, 且可访问其他方的验证公钥.

3.3 存活性

定理1 (ZG 协议满足存活性) ZG 协议存在成功运行实例, 且在该实例中发方A和收方B均可收到自己想要的证据.

证明: 当发方A和收方B遵照ZG 协议步骤执行交互时, 协议能够成功运行.

3.4 不可否认性

由定理2、3 和定义8, 可知ZG 协议满足不可否认性.

3.5 公平性

定理4 (ZG 协议满足公平性) ZG 协议执行完成后, 要么发方A和收方B都能收集到自己想要的证据, 要么都收集不到任何对己有利的证据, 即POO∈OiBiffPOR∈OiA, 0≤i ≤5.

证明: 分两种情况讨论: 协议成功执行和协议中断执行.

3.6 时限性

综上所述, 利用扩展ZQZ 逻辑方法分析到ZG 协议满足存活性、不可否认性、公平性, 但不满足时限性, 对收方不公平, 是逻辑存在局部错误的协议, 所获分析结论与既有事实相符.

4 KPB 协议分析

4.1 协议描述及假设集

针对ZG 协议存在的时限性问题, Kim 等人[32]通过向协议消息中添加时间限制信息的办法对其进行了改进. 改进后的协议(KPB 协议) 描述如下:

协议执行后,A和B收集到的证据与ZG 协议相同. 由于该协议没有改变原协议的交互步骤与证据信息, 故其提供的存活性、不可否认性和公平性级别不会低于原协议. 然而, 由于其在协议消息中添加了时间约束信息, 故需分析该协议是否如Kim 等人宣称的那样, 弥补了原协议不满足时限性的问题.

4.2 时限性

由定理7 和定理8 可知, 该协议满足时限性. 即, Kim 等人通过向Zhou-Gollman 协议中添加时间约束信息, 解决了原协议不满足时限性的问题.

综上所述, 利用扩展ZQZ 逻辑方法分析到KPB 协议同时满足不可否认协议的四个安全性质, 是逻辑正确的协议, 所获分析结论与既有事实相符.

5 YLL 协议分析及改进

5.1 协议描述及假设集

文献[14] 提出了一个基于区块链的多方不可否认协议(简称YLL 协议). 简要描述如下:

5.2 收方时限性

文献[14] 认为YLL 满足时限性, 并指出“协议的所有参与方都可以在时刻T之前完成协议, 而不影响公平性”. 此处我们使用扩展ZQZ 逻辑分析出其并不能为收方提供如协议设计者所宣称的时限性.

定理9 (YLL 协议不满足收方时限性) 在YLL 协议的任意运行实例中, 当收方所在网络不可用的时间长度t0大于发方所承诺的收方可从链上检索到交易信息的最迟期限T与信息上链的真实时间TOPEN之间的时间差(T-TOPEN) 时, 即使T ≥TOPEN, 收方也无法在时刻T之前完成协议且不影响公平性.

其中TBi是Bi规定的A将OPEN(in:TAx) 广播到区块链的最迟期限. 利用扩展ZQZ 逻辑方法容易证明改进后的协议遵循四个安全性质.

6 方法比较

表1 对逻辑推理、状态检测、定理证明和进程代数这四类分析不可否认协议逻辑正确性的常见方法进行了比较. 其一, 作为一种逻辑推理类方法, 扩展ZQZ 逻辑在抽象程度高、无状态爆炸、分析难度低等方面较其它三大类方法均具有明显的优势; 其二, 作为一种类Kailar 逻辑, 扩展ZQZ 逻辑是基于责任分析而非信念推理, 因而较SVO 逻辑及变体更适用于分析不可否认协议逻辑正确性; 其三, 相较于原ZQZ 逻辑, 扩展ZQZ 逻辑能够描述与分析时间约束关系, 其不仅能够分析协议的存活性、不可否认性和公平性,而且还能分析时限性.

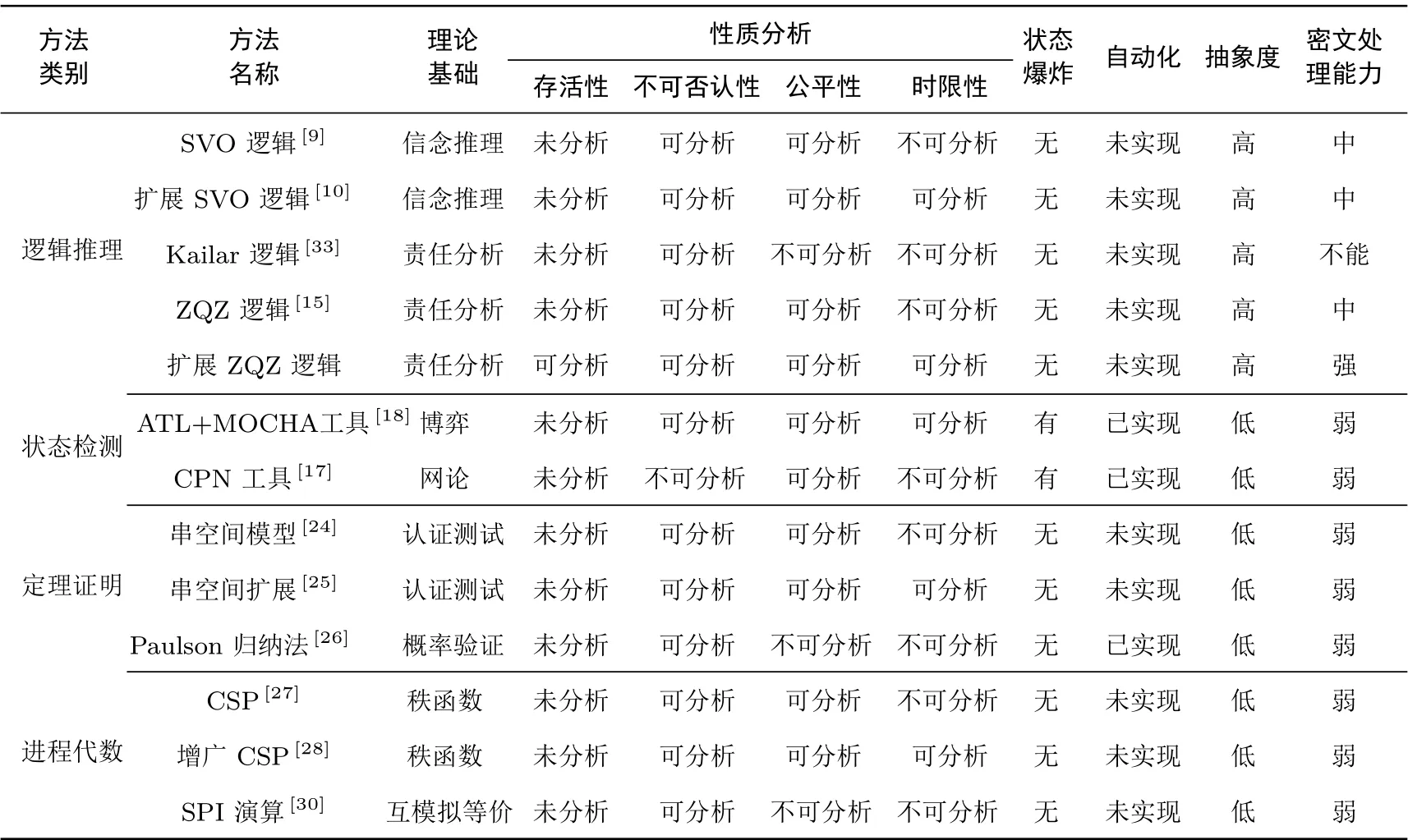
表1 不可否认协议常见形式化分析方法比较Table 1 Comparison of common formal analysis methods for non-repudiation protocol

7 结束语

通过向ZQZ 逻辑添加时间表达式, 提出了一种适用于不可否认协议分析的扩展ZQZ 逻辑方法, 给出了推理规则扩展和安全性质模型, 并以两个两方不可否认协议和一个基于区块链的多方不可否认协议为实验对象, 介绍了将该逻辑方法应用于不可否认协议分析的使用过程. 与原ZQZ 逻辑方法相比, 该方法除了继承了面向责任分析、初始假设形式化、抽象程度高、无状态爆炸、可分析协议的不可否认性和公平性等特征外, 还可分析协议的存活性和时限性, 并能提供更强的密文处理能力.

下一步工作是, 针对多方不可否认协议中共谋实体间的合作博弈, 以及共谋者与被排斥者之间的非合作博弈本质, 拓展基于博弈论的交替转换逻辑, 并将其引入到扩展ZQZ 逻辑中, 使其能够分析多方不可否认协议的无排斥性和抗合谋性等特殊性质, 以减轻目前多方电子支付中存在的网络欺诈现象.