启动阀蝶盘密封失效机理研究

胡 攀, 袁洪滨, 王运卯, 程晓辉

（西安航天动力研究所，西安，710100）

0 引 言

CZ-2F火箭一二级发动机启动阀是发动机系统的关键组件之一，安装在发动机泵前管路中，属常闭蝶型电爆阀门。在发动机起动前，起着隔离推进剂与发动机的作用；发动机起动时，由电爆管驱动打开启动阀蝶盘，并使之锁位在90°左右位置，使推进剂进入发动机腔内，发动机开始工作。启动阀门可靠工作与否直接关系到发动机工作的成败。启动阀门结构简图见图1。

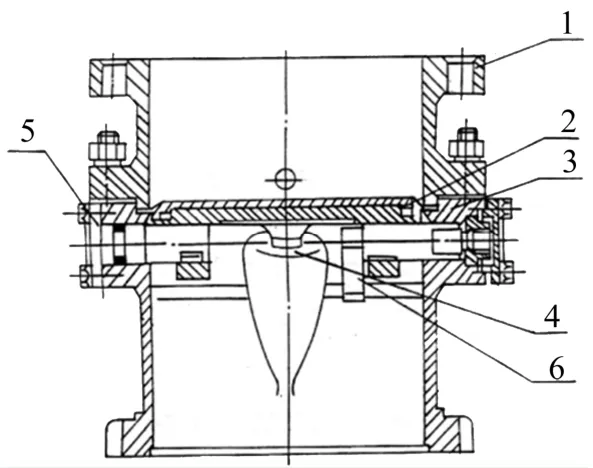
图1 启动阀门结构简图Fig.1 Principium of Starting Valve

启动阀的蝶盘薄壁刻痕处剩余厚度较小，因此该部位在长期贮存过程中，受环境温度变化、湿度变化及空气中氧等作用，存在表面氧化腐蚀的风险；另外由于启动阀蝶盘密封处密封通过12个螺栓进行压紧，若该处出现蠕变，密封应力下降到一定程度，则会使启动阀门密封隔离推进剂的作用失效，同时对电爆正常撕裂及锁位产生一定影响，影响蝶盘打开及锁位。

连接蝶盘所使用的螺栓和螺母材料分别为高强铝合金和高强钢，高强铝合金出现蠕变特性的温度为100 ℃以上，高强钢出现蠕变特性的温度需达到450 ℃以上，而纯铝在室温下即可表现蠕变特性，因此只考虑蝶盘纯铝的蠕变特性进行分析研究。

1 问题分析

根据启动阀的工况，其密封性能主要受两个因素的影响：蝶盘的蠕变以及刻痕处氧化腐蚀共同导致的预紧力的松弛。

a）刻痕在预紧力作用下的腐蚀。即纯铝和空气中的氧、水分发生化学反应，导致薄壁刻痕剩余厚度减小，当减小到一定程度，刻痕不能承受工作前的介质压力，导致刻痕破裂，推进剂泄漏，发生失效；

b）蝶盘薄壁在预紧力作用下保证密封，纯铝在常温下表现出应力松弛的现象，即密封部位的弹性密封应力（比压）随着时间增加逐渐减小，当放置一段时间后，密封部位的应力下降到不足密封启动阀前的介质时，发生外泄漏，密封部位失效。

根据以上分析，在贮存条件下的应力松弛和腐蚀影响到启动阀密封可靠性。

2 研究内容

根据以上分析，研究方案主要包括以下几个方面的内容：

a）薄壁刻痕蠕变速率检测和铝合金蠕变速率理论曲线拟合。依据测量得到的应变速率变化通过理论公式获得薄壁刻痕结构铝合金常温装配应力下蠕变速率双对数曲线。

b）铝合金氧化层厚度检测。

c）密封性力矩摸索试验。

d）仿真计算：综合上述研究结果，对刻痕部位进行建模，模拟装配和贮存环境下刻痕密封性能变化情况，得到阀门能够正常密封的预估寿命。

3 蠕变速率测试及分析

为了获得启动阀在密封状态下的蠕变情况，先对其应力状况进行分析。

螺栓的预紧力矩：

式中为拧紧力系数，这里取0.2；P为预紧力；为螺纹公称直径。

根据启动阀的安装工况计算得到总预紧力。

作用在膜片上的预紧应力为

式中为接触区域面积；为总预紧力。

在应力的作用下金属的蠕变通常遵循幂律蠕变（Power law creep）：

当得到某压力下的蠕变变形后通过拟合-的曲线后求导可以得到，则可以求出蠕变常数为

则在任意一应力下的蠕变情况都可以拟合为

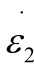
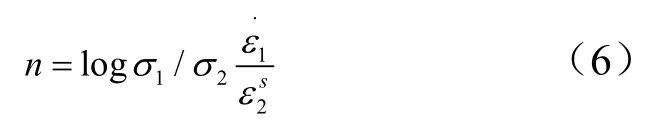
此时的任意一应力下的蠕变情况可以修正为

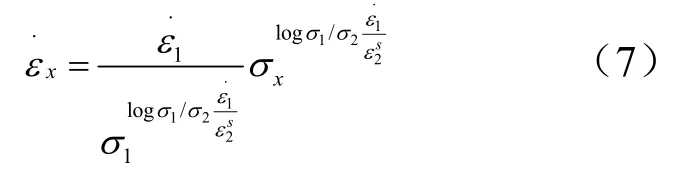
电子蠕变松弛试验机主要用于金属材料的高温拉伸蠕变，持久强度、松弛、低周疲劳和蠕变疲劳试验。其配备的加热炉也可以满足不同恒定以及变温条件下的蠕变试验。获得任意一压应力下的蠕变速率，可以帮助获得密封蝶盘的蠕变情况。在前期的小应力测试下，发现其趋势基本符合小应力下的蠕变曲线，小应力下的蠕变曲线如图2所示。下一步可以通过继续增大压应力以获得高应力作用下的蠕变曲线，这样便可以根据：

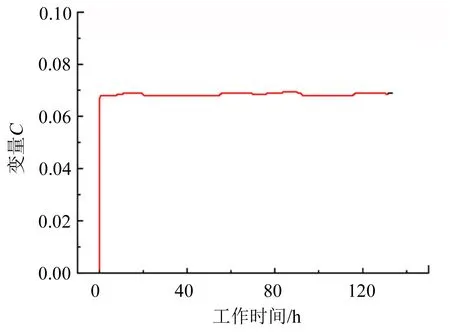
图2 小应力下的铝材料蠕变曲线Fig.2 Aluminum’s Creeping Line of Low Stress

拟合出该应力范围内任意一压应力的蠕变速率。

从而得到蠕变速率与应力的对数关系：

式中，为拟合后得到的系数，通过式（9）便可以计算低应力下的蠕变速率，得到临界应变下的蠕变时间（寿命）。

4 铝表面氧化层试验

启动阀刻痕在预紧力作用下的腐蚀，即纯铝和空气中的氧、水分发生化学反应，导致薄壁刻痕剩余厚度减小。由于在氧化层生长过程中已生长的氧化铝层会起到隔离空气的作用，氧化速率会逐渐降低。现有的测量氧化铝厚度的方法一般采用光学测量，包括直读式目镜测微尺、金相显微镜测厚等方法。但由于自然情况下氧化铝的厚度较小，使用这些方法误差较大，因此需采用XPS（X射线光电子能谱）、TEM（电子透射显微镜）或者SEM（扫描电子显微镜）等方法测量。按照GB/T6462-2005《金属和氧化物覆盖层：厚度测量-显微镜法》标准的规定，把实验样品切割、研磨并抛光，制成截面金相样后置于显微镜或者电镜下进行观察，沿长度方向选取5点进行测量，选取平均值作为氧化层的平均厚度。

为了能顺利在SEM（扫描电子显微镜）下进行观察，本实验首先将将铝棒（直径20 mm）先切割为 40 mm长度的样品，然后依次采用粒径为200 μm、800 μm、2000 μm的水磨砂纸进行初步打磨（见图3），铝样品表面的光洁度在每个阶段都有了明显程度的提高。再将铝棒切为厚度为1 mm的薄片，并在空气中分别放置时间为24 h、48 h和72 h后，通过抛光侧面进行氧化层的观察。由于SEM样品台的限制，测试前还需要将薄片切为1/4圆的形状方便观察，如图4所示。

图3 初始样品制备Fig.3 Original Sample Piece Preparation

图4 SEM样品制备Fig.4 SEM Sample Piece Preparation

由于金属和氧化物之间都一定存在着强大的粘结力，并且铝元素具有天然的活泼型，当暴露在氧气中时，开始的氧化增长速率是很快的，接着就是一个显著的速率减缓，当达到一定临界厚度后，增长将会停止或近乎停止。

图5为1035铝表面氧化层厚度随时间的变化。氧化层厚度在24 h内已经达到稳定厚度64 μm，不到总厚度的10%。因此其对密封件中的应力分布及蠕变过程的影响可以忽略。所以，在有限元建模中，可不考虑氧化层部分。

图5 铝表面氧化层变化Fig.5 The Change of Aluminum Surface’S Oxidizing Layer

5 密封性力矩摸索试验

利用批次典型试验和试车后产品，进行10台阀门螺母的拧紧力矩和泄漏之间的关系，校核结果见图6。出现泄漏的产品力矩均低于10 N·m。

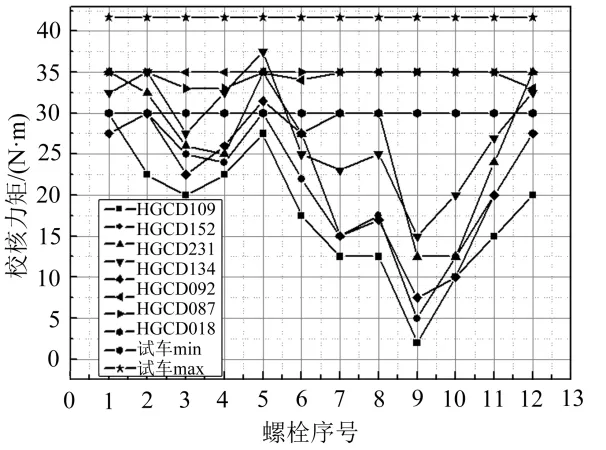
图6 力矩校核结果Fig.6 The Test Result of Force Moment

6 有限元法计算结果讨论

蠕变的有限元计算主要是利用实验的材料参数后，再将所获得的参数使用于有限元的分析模型中，以求获得其应力、应变、蠕应力、蠕应变等内部结构经外力、时间或温度所造成的效应。蠕变分析通常采用3种蠕变定律描述粘塑材料行为。幂次法则模式（Power-law Model）可应用于仿真等温与固定负载下的蠕变行为，根据其所采用的定律可分为时间硬化率（Time Hardening）及应变硬化率（Strain Hardening）关系式。非等温情况下则使用Garofalo-Arrhenius双曲正弦法则模式。

首先要选取适合的模型。图7为有限元网格。当应力保持不变时，选取Power-law模型中的时间硬化率模型最合适。针对本项目的研究内容，在进行有限元计算时，选取时间硬化率选项：

图7 有限元网格Fig.7 Finite Element Grids

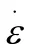
由于本研究中铝发生了大的塑性变形，因此划分网格时选取二次四面体单元，对于大变形和接触问题，这种单元是强健的，展示了很小的剪切和体积自锁，选用弹-塑性分析模型。铝合金采用双线性强化弹-塑性力学模型，即其应力应变曲线有两个斜率，弹性斜率和塑性斜率，也称为弹性模量和切向模量。双线性强化模型的数学表达式如下：

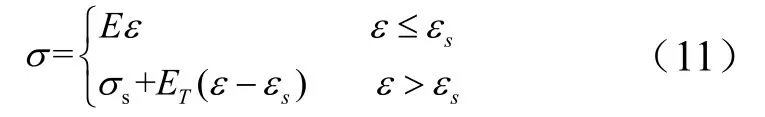
式中为应力，GPa；为应变；为弹性模量，GPa；E为切向模量，GPa；为屈服应变。

通过静态加载过程的分析后，结构中将产生一个应力场，接下来可以进行蠕变过程的计算。蠕变过程的计算主要分为两个过程：获得该结构材料的蠕变模型参数和建立蠕变分析仿真模型。材料的蠕变参数可通过蠕变测试试验得到。由于蠕变是一个时间相关的过程，因此必须计入时间；同时蠕变又是一个惯性效应不明显的过程，即结构的加速度效应不用考虑。

由于密封失效与膜片位于密封区域的应力直接相关，因此计算结束后，取膜片密封面上的应力分布进行分析。

图8为静态加载结束后，膜片密封面上的应力分布，可以看出最大应力为41.6 MPa。

图8 密封面上的应力分布（静态）Fig.8 The Stress of Sealing Surface (Static Situation)

随着蠕变时间增加，膜片中的最大应力值减小，图9为最大应力随着蠕变时间的变化计算曲线。从图9中可以看出，最大应力的减小速率随着蠕变时间的增加而减小，这是由于，随着蠕变过程的进行，膜片中的应力逐渐减小，因此材料的蠕变速率也跟着减小，这反过来又导致应力减小的速率也减小。从图9中可以看出，应力减小速率越来越小，当蠕变时间增加至4×10s时，膜片中的应力基本稳定在14.5 MPa。

实际工况下，当螺母力矩降低为10 N·m，密封失效，对应的压力载荷为10.8 MPa；仿真计算密封面最大应力下降至14.5 MPa趋于稳定且不再下降，此时应力离10.8 MPa还有一定裕度。因此，启动阀蝶盘长期密封寿命理论上为无限寿命。

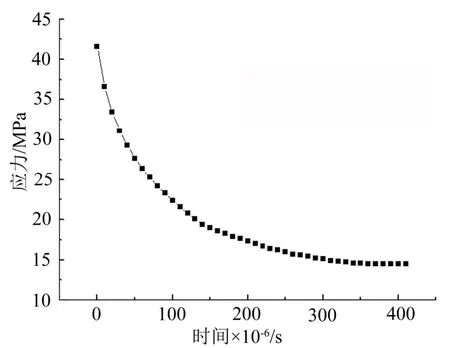
图9 密封面最大应力随蠕变时间变化（动态）Fig.9 The Changing Stress of Sealing Surface(Dynamic Situation)

7 结束语

启动阀蝶盘刻痕密封失效的机理研究表明，启动阀蝶盘部位的密封寿命为无限寿命；可以通过校核测量启动阀安装螺母的力矩大小来监控蝶盘的密封性能，掌握启动阀工作前状态。