载人火箭推力矢量调整偏差对有塔逃逸安全性影响分析

柳海龙，容 易，张 智，顾名坤，陈牧野

（1. 北京宇航系统工程研究所，北京，100076；2. 中国运载火箭技术研究院，北京，100076）

0 引 言

长征二号F运载火箭是中国现役唯一的载人运载火箭，逃逸塔位于整个火箭的头部，是有塔逃逸飞行器的重要组成部分。逃逸塔的功能是在时序-15 min至120 s期间为逃逸飞行器提供主要的逃逸动力，约120 s与火箭分离。

逃逸塔由3种型号的固体发动机组成，其中逃逸主发动机为前置4喷管的固体发动机，由于逃逸主发动机生产制造和装配的误差，实际上逃逸主发动机的合成推力线并不与发动机的轴线重合，这种偏差是随机的。同时有塔逃逸飞行器的质心也不在轴线上，而且每发任务均存在一定的差异性。有塔逃逸飞行器在有动力逃逸飞行过程中将产生一个绕横轴的翻转力矩，这个力矩是干扰力矩且它的方向是随机的。理论分析表明，在发射台附近逃逸时，这个干扰力矩将影响逃逸飞行器的逃逸高度和逃逸飞行姿态。因此对逃逸飞行器主发动机的推力线进行调整，即推力矢量调整，使之与有塔逃逸飞行器质心不重合度控制在一定的范围内，是一个提高逃逸飞行器性能和优化载荷设计的方法。但在工程实践中，逃逸飞行器的质心位置是通过理论计算获得的，而理论计算时用到的质量质心数据多为经验值，不是每发箭的实测值。因此，即使开展推力矢量调整工作，只能将逃逸主发动机的推力线与逃逸飞行器质心的不重合度控制在一定范围内，不能实现逃逸主发动机的合成推力线完全通过逃逸飞行器质心的理论情况，这种不重合度对逃逸飞行器的逃逸高度和姿态有何影响，哪个质心方向的偏差因素对逃逸安全性影响更敏感是需要研究的内容。

1 推力矢量调整原始参数

1.1 坐标系定义

首先定义一个坐标系，坐标原点位于逃逸主发动机后法兰处球面的球心；轴和箭体纵轴重合，顺航向方向为正；轴位于Ⅰ-Ⅲ基准面内，指向Ⅲ基准线为正；轴按右手法则确定，如图1所示。

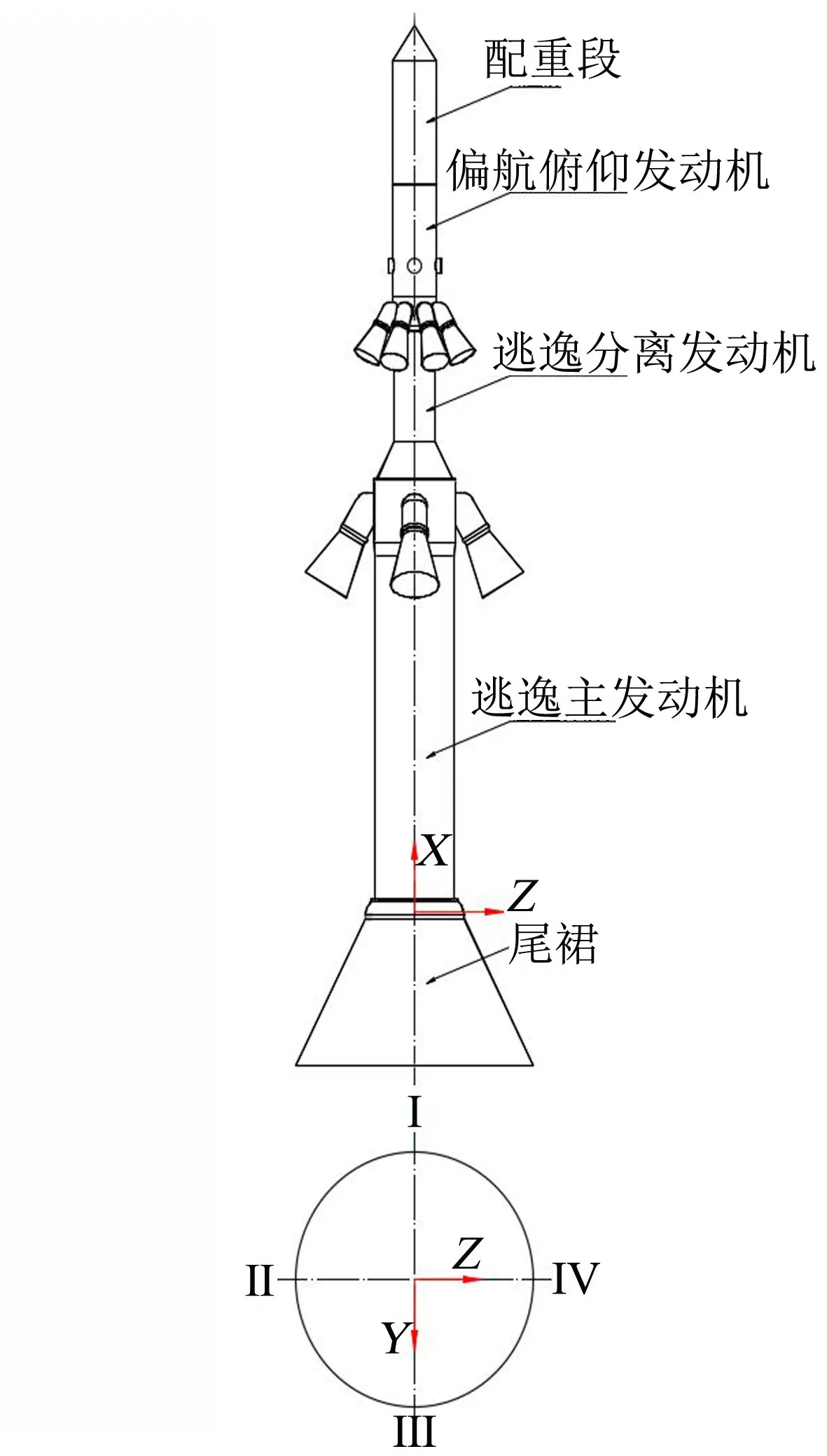
图1 推力矢量调整坐标系定义Fig.1 Definition of Thrust Vector Adjustment Coordinate System

1.2 推力矢量调整参数

对于逃逸主发动机，多个喷管呈中心对称分布，理论推力作用点是标称设计状态下各喷管几何轴线的交点，其坐标记为（,0,0），由喷管布局及其结构尺寸确定。将坐标系平移，使其坐标原点与理论推力作用点重合，推力矢量参数示意见图2。

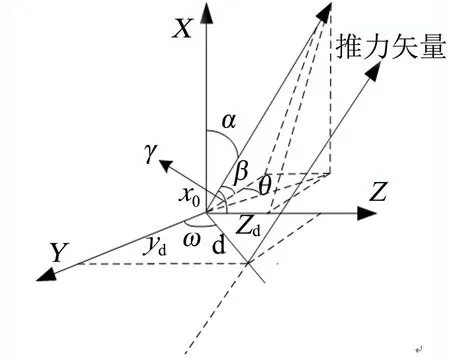
图2 逃逸主发动机推力矢量示意Fig.2 Escape Main Engine Thrust Vector Display

推力矢量参数包括推力线偏斜角、推力线偏斜方位角、推力线横移和推力线横移方位角4个参数。具体获取方法如下：

a）推力线偏斜角为逃逸主发动机推力矢量与轴的夹角，由固体发动机承制单位通过测量获取。

b）推力线偏斜方位角。

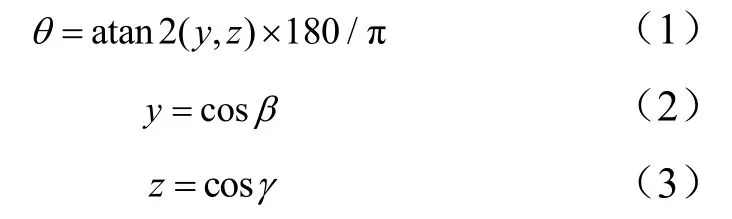
式中 atan2(,)为反正切函数，其返回值的范围为（-π,+π）；为推力矢量与轴的夹角，由固体发动机承制单位通过测量获取；为推力矢量与轴的夹角，由固体发动机承制单位通过测量获取。

c）推力线横移。

式中y为实际推力线与通过理论推力作用点并垂直于轴的平面交点的坐标值，由固体发动机承制单位通过测量获取；Z为实际推力线与通过理论推力作用点并垂直于轴的平面交点的坐标值，由固体发动机承制单位通过测量获取。

d）推力线横移方位角。

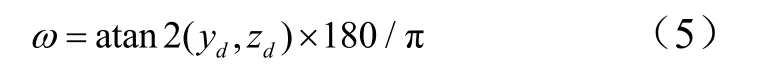
1.3 逃逸塔-尾裙质量特性

计算逃逸飞行器上部的质量特性，指不包含尾裙的逃逸塔，位于推力矢量调整球面上部，其质量特性由组合头部动力装置及配重段的质量和质心合成而获得，合成方法如下：

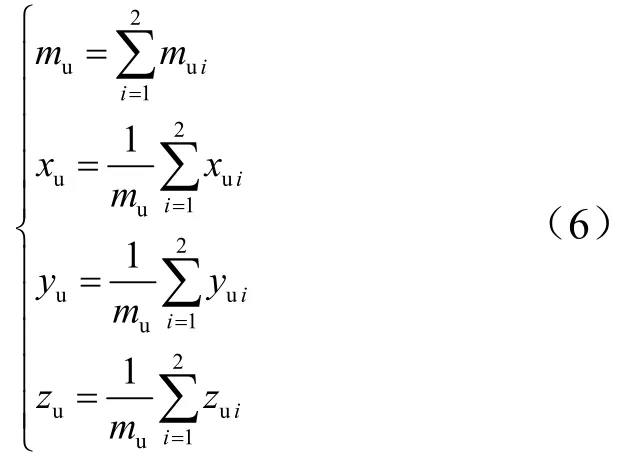
式中为逃逸飞行器上部质量；,,为逃逸飞行器上部质心坐标；1=为组合头部动力装置，其质量和质心均由固体发动机承制单位通过测量获取；2=为配重段，其质量由配重块质量和配重筒段及头锥质量合成，配重块质量按照实际安装的配重块计算，配重筒段及头锥的质量使用总体原始数据给定的理论值；其质心使用原始数据给定的理论值。

1.4 无塔逃逸飞行器+尾裙质量特性

计算逃逸飞行器下部的质量特性，指包含了尾裙的无塔逃逸飞行器，位于推力矢量调整球面的下部，其质量特性分别由尾裙、整流罩逃逸部分、飞船返回舱和轨道舱的质量和质心合成，合成方法如下：

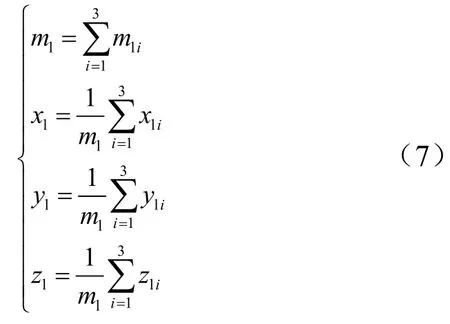
式中为逃逸飞行器下部质量；,,为逃逸飞行器下部质心坐标；1=为尾裙，其质量和质心均使用总体原始数据给定的理论值；2=为整流罩逃逸部分，其中整流罩前锥段、前柱段、后锥段、上支撑机构、下支撑机构、栅格翼、阻尼器及其释放机构、高空逃逸发动机、高空分离发动机等结构的质量使用实测值，其余部分的质量使用总体原始数据给定的理论值；质心使用总体原始数据给定的理论值；3=为飞船返回舱和轨道舱组合体，质量和质心均使用飞船系统提供的实测值。

1.5 逃逸主发动机对接法兰位移测量点

位移测量点共计3个，布局见图3。

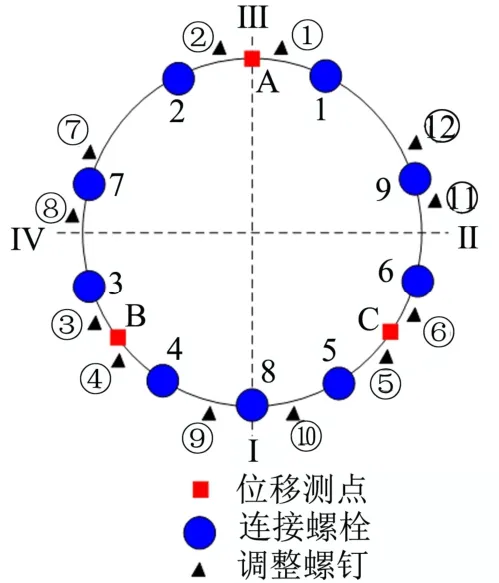
图3 推力矢量调整面对接示意Fig.3 Thrust Vector Adjustment Docking Relationship Display

测点坐标由结构尺寸决定，使用结构设计要求中规定的理论值，3个测点的坐标表示如下：

2 推力矢量调整算法

通过绕轴，轴的2次旋转，可使坐标系中的任意一条直线通过一个固定的点。这个直线就是逃逸主发动机的推力线，用两点的坐标来表示，即逃逸主发动机实际推力线和理论作用点平面的交点坐标（X，Y，Z）和逃逸主发动机实际推力线与逃逸飞行器质心平面的交点坐标（X，Y，Z），固定点就是调整后合质心的位置（，，），这3点的初始坐标：

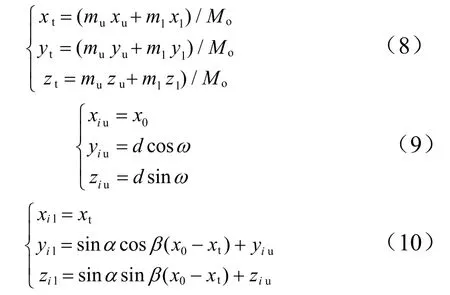
假设逃逸主发动机推力线绕轴的转角为，绕轴的转角为。则旋转后、两交点、上部的质心3个位移测量点的坐标为

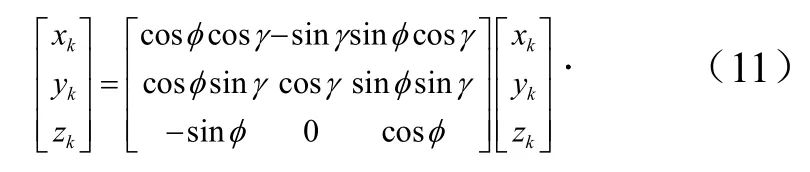
式中=a,b,c,l,u,u，a,b,c为3个位移测量点坐标的下标。

将新获得的上部质心代入式（8），便可以获得新的合质心位置，令为（，，）。通过新获得的两个交点，可以写出空间的两点式直线方程：

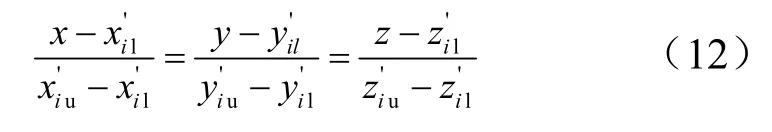
令=便可以获得两个方程，解出所需的两个转角。再利用式（11）求出a,b,c 3个测量点的位移。

解析的方法从理论上讲可以求出问题的解，但是要求解的两个关键参数和是隐含在三角函数中的，因此求解很困难。在实际软件算法求解应用中采用的是数值逼近的方法。

数值逼近的方法在原理上与解析方法是一致的，只是采用了逐步逼近搜索的方法。首先给定一个小的旋转角度，再根据上述公式计算下一个点，然后比较新获得的推力线与合质心平面的交点与和质心的向、向距离，若距离减小，说明方向正确，继续加大步长前进，若发现距离增大，则反向搜索，步长取原来的1/2，直到其满足给定的精度要求。

3 推力矢量调整工程实现

3.1 测量系统

推力矢量调整测量系统主要由推力矢量调整测量仪、采集设备、预紧力等效器、位移传感器、打印机、电缆等组成，如图4所示，其中，推力矢量调整锁紧螺栓连接逃逸塔与尾裙，同时在其内壁粘贴应变片，输出预紧力，监测预紧力加载数值；位移传感器输出位移，监测3个测点的位移值。

选择2016年6月—2018年6月我院收治的120例行冠状动脉检测患者，男64例，女56例，年龄为43～66岁，平均年龄为（54.5±4.9）岁。纳入标准：（1）均符合冠状动脉疾病的临床诊断标准；（2）未患有其他心脑血管疾病。排除标准：（1）患有严重的脏器病变；（2）患有严重的意识障碍症状。患者家属在了解相应的检测方式后签署知情同意书，同时由医院伦理委员会对本实验进行监督；使用统计学软件对患者进行分析处理。

图4 推力矢量调整测量系统Fig.4 Thrust Vector Adjustment Measurement System

3.2 结构设计

逃逸主发动机与尾裙的连接面同时也是逃逸主发动机推力矢量的调整面，其结构见图5。

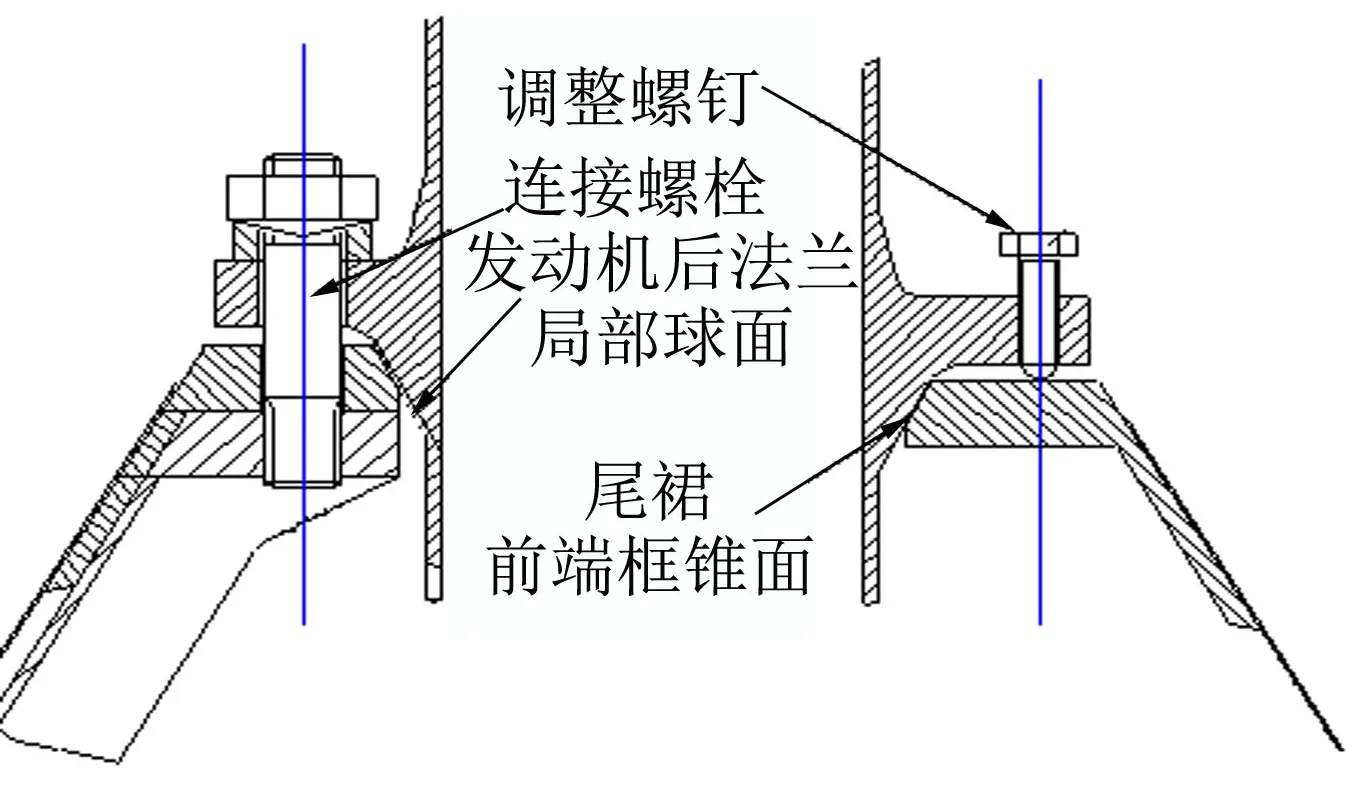
图5 逃逸主发动机与尾裙对接面Fig.5 Escape Main Engine and Tail Section Structure Docking Relationship Display

连接结构设计采用了球面与锥面接合的原理。在发动机法兰的后面是一圈半径为SR402的局部球面，尾裙的上端框有高度20 mm的25°锥面。在逃逸主发动机的后法兰上有调整螺钉，它可以使发动机绕其球面的中心在尾裙的锥面内转动。

两个对接面的连接螺栓（即推力矢量调整螺栓）是M30的双头螺栓，下端连在尾裙上端框下的钢钉接头上，上端穿过发动机法兰的通孔，与之配套的是一种非标的下端有球面的螺母，螺母的下方有一球窝座，以适应调整的需要。这种螺栓除了起连接作用外，本身又是一种测力传感器，在连接锁紧时可以进行高精度的预紧力测量。

4 偏差影响仿真分析

在推力矢量调整过程中，使用原始参数作为输入条件，其中固体发动机的推力作用线为固体发动机单位通过实测获得，该取值非常准确，可以不考虑偏差；而逃逸飞行器的质量、质心特性是通过经验值计算获得，因此质量质心特性存在较大偏差的可能，本章节对质量质心特性偏离真实值的情况下，对有塔逃逸飞行器逃逸安全高度和姿态的影响开展仿真分析。

4.1 初始偏差的设定

为了研究有塔逃逸飞行器质量、质心特性偏差对逃逸安全高度和姿态影响的敏感性，人为设定如下初始偏差：

a）逃逸飞行器质量特性偏差：±50 kg。

b）逃逸飞行器纵向质心偏差：±500 mm。

4.2 仿真分析工况

依据设定的初始偏差，对如下5个工况进行仿真分析，仿真分析工况见表1。

表1 仿真分析工况Tab.1 Types of Simulation Analysis Conditions

4.3 仿真分析结果

以Y12火箭逃逸飞行器的原始参数作为仿真分析的基准工况，针对0-0高度逃逸飞行状态，对上述5个工况下有塔逃逸飞行器的逃逸安全高度和姿态结果进行仿真分析。

4.3.1 无推力矢量调整仿真结果

假设不做推力矢量调整，逃逸主发动机通过端面对接法兰直接安装在尾裙上，此工况下有塔逃逸飞行器在0-0高度逃逸飞行中于20.475 s达到最大逃逸高度1747.9 m，逃逸高度曲线如图6所示；方向的最大偏航角速度为12.4（°）/s，偏航角速度曲线如图7所示；当逃逸到最大高度时，有塔逃逸飞行器在方向偏转235.5°，偏转角位移曲线如图8所示。

图6 逃逸高度曲线（无推力矢量调整）Fig.6 Escape Height Curve-no Thrust Vector Adjustment

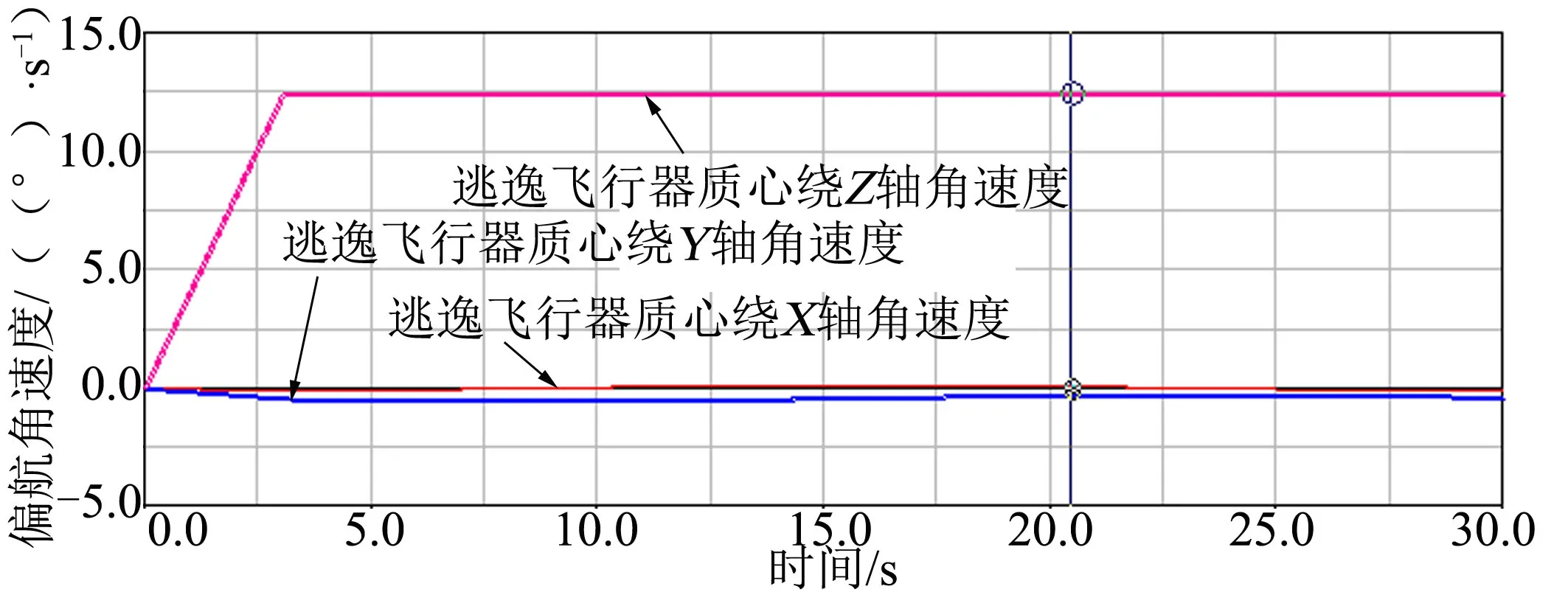
图7 偏航角速度曲线（无推力矢量调整）Fig.7 Attitude Angular Velocity Curve-no Thrust Vector Adjustment

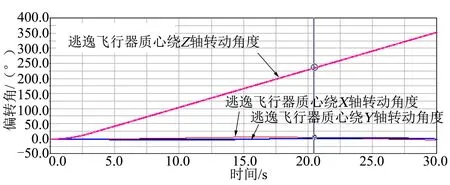
图8 偏转角位移曲线（无推力矢量调整）Fig.8 Attitude Angular Displacement Curve-no Thrust Vector Adjustment

通过仿真分析表明，如果不对有塔逃逸飞行器开展推力矢量调整工作，能实现的最大逃逸高度虽然略显偏低，但仍然在安全逃逸高度允许的偏差之内；最危险的情况是在翻转干扰力矩的作用下，有塔逃逸飞行器姿态发生翻滚，不满足安全逃逸的设计要求。

4.3.2 有推力矢量调整仿真结果

通过开展推力矢量调整工作，使得逃逸主发动机的推力线通过有塔逃逸飞行器的质心，此工况下有塔逃逸飞行器在0-0高度逃逸飞行中于20.701 s达到最大逃逸高度1787.8 m，逃逸高度曲线如图9所示；方向的最大偏航角速度为0（°）/s，偏航角速度曲线如图10所示；当逃逸到最大高度时，有塔逃逸飞行器在方向偏转0.013°，偏转角位移曲线如图11所示。

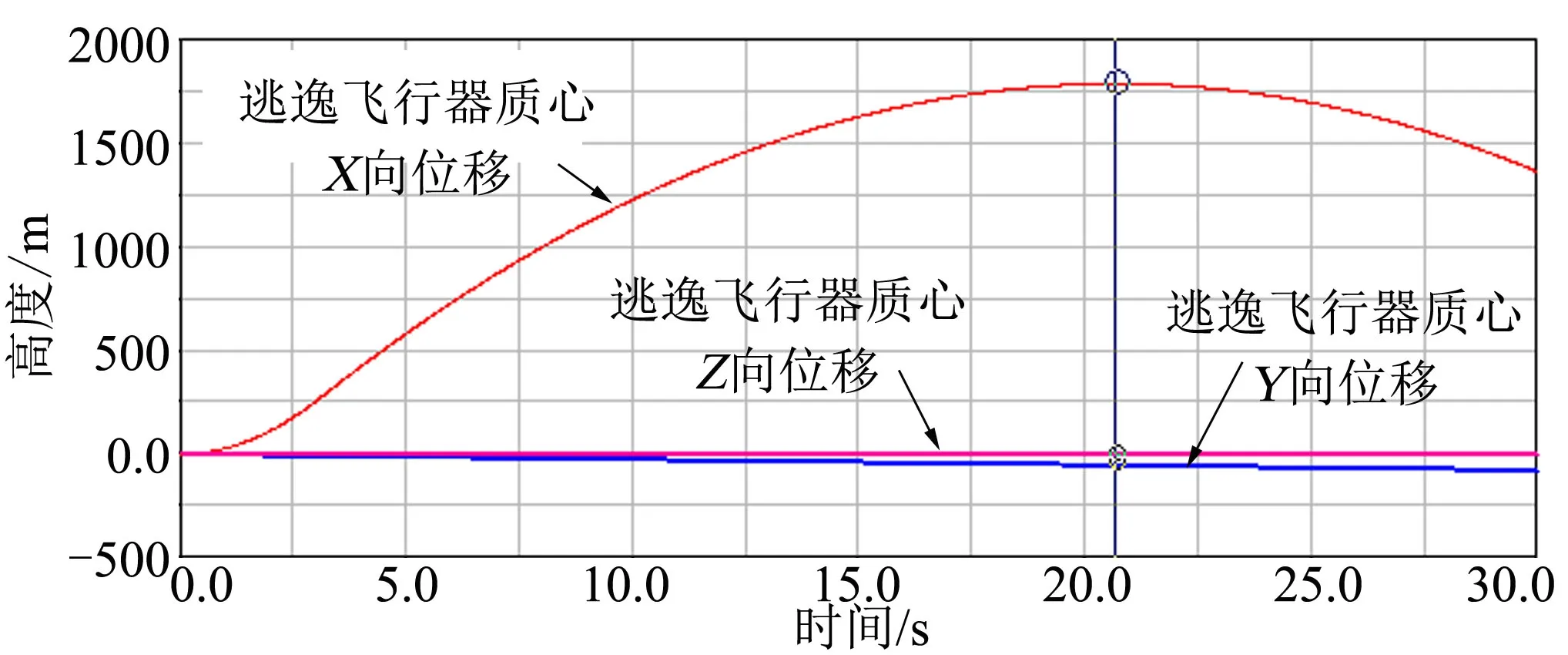
图9 逃逸高度曲线（推力矢量调整后）Fig.9 Escape Height Curve-thrust Vector Adjustment

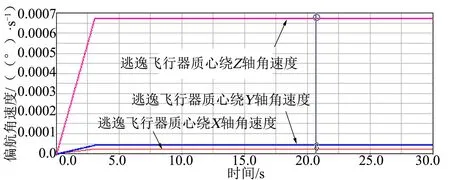
图10 偏航角速度曲线（推力矢量调整后）Fig.10 Attitude Angular Velocity Curve-thrust Vector Adjustment

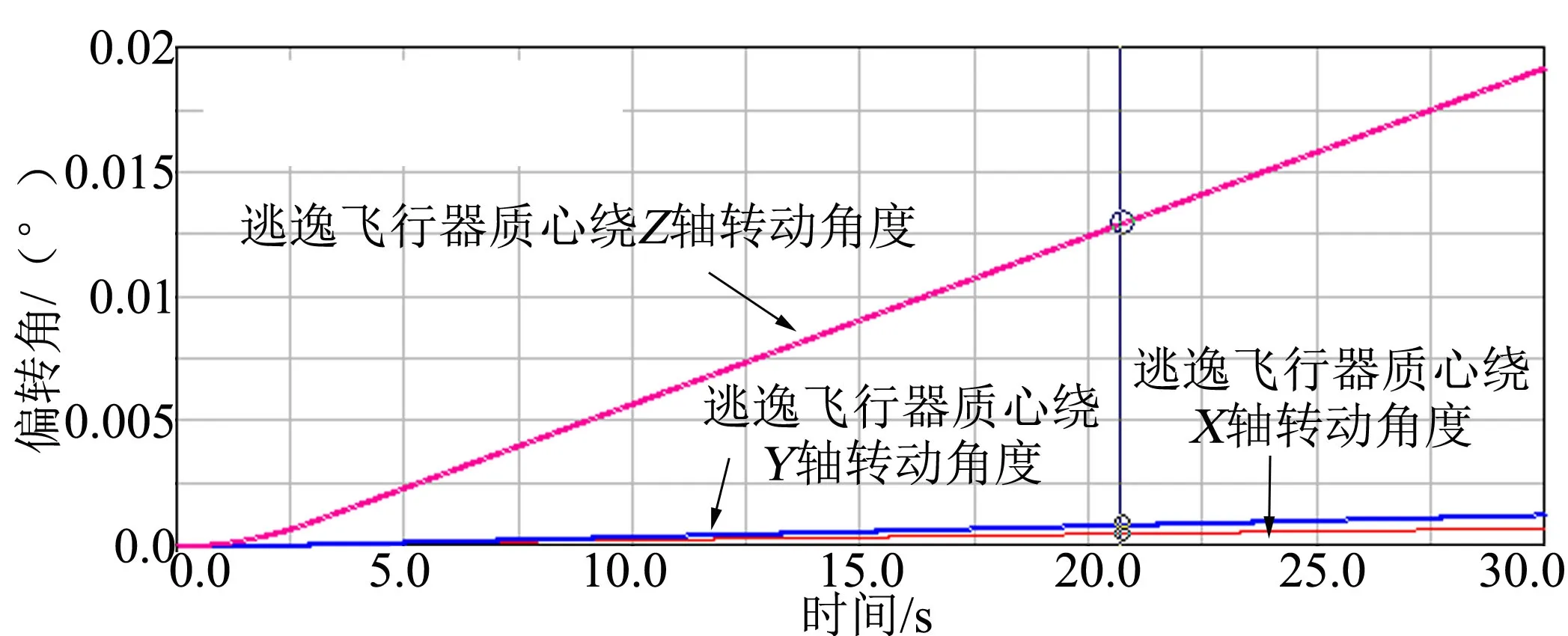
图11 偏转角位移曲线（推力矢量调整后）Fig.11 Attitude Angular Displacement Curve-thrust Vector Adjustment

通过仿真分析表明，通过开展推力矢量调整工作，有塔逃逸飞行器的最大逃逸高度提高了39.9 m，且有塔逃逸飞行器在逃逸过程中姿态保持姿态稳定，满足安全逃逸的设计要求。

4.3.3 质量偏差工况仿真结果

依据设定的初始偏差，在开展推力矢量调整的情况下，如果逃逸飞行器的真实质量特性偏离计算输入值±50 kg，此时有塔逃逸飞行器在0-0高度逃逸飞行中的逃逸性能参数与无偏差工况的对比情况见表2。

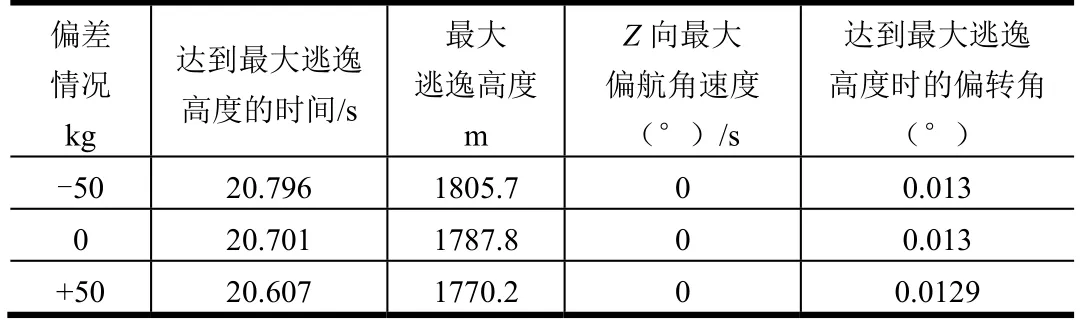
表2 质量特性偏差工况下逃逸性能参数对比Tab.2 Comparison of Escape Performance Parameters under the Condition of Mass Characteristic Deviation

通过仿真分析表明，逃逸飞行器质量特性偏差只影响最大逃逸高度，对逃逸飞行器的姿态特征无影响。当逃逸飞行器的质量偏差从-50 kg到+50 kg变化时，最大逃逸高度从1805.7 m降低至1770.2 m，因此推力矢量调整工作中可忽略质量特性偏差带来的影响。

4.3.4 纵向质心偏差工况仿真结果

依据设定的初始偏差，在开展推力矢量调整的情况下，如果逃逸飞行器的纵向质心位置偏离计算输入值±500 mm，此时有塔逃逸飞行器在0-0高度逃逸飞行中的逃逸性能参数与无偏差工况的对比情况见表3。

表3 纵向质心偏差工况下逃逸性能参数对比Tab.3 Comparison of Escape Performance Parameters under the Condition of Longitudinal Centroid Deviation

通过仿真分析表明，逃逸飞行器纵向质心偏差对最大逃逸高度影响不明显，但对逃逸飞行器的姿态特征有一定影响。当逃逸飞行器的纵向质心偏差从 -500 mm到+500 mm变化时，达到最大逃逸高度时逃逸飞行器的偏转角在-29.6417°至+29.6785°变化，因此推力矢量调整工作中纵向质心偏差会导致逃逸飞行器姿态角放大，但在逃逸飞行过程中姿态变化缓慢，不会引起逃逸飞行器的姿态急剧变化。

4.3.5 横向质心偏差工况仿真结果

依据设定的初始偏差，在开展推力矢量调整的情况下，如果逃逸飞行器的横向质心位置偏离计算输入值±20 mm，此时有塔逃逸飞行器在0-0高度逃逸飞行中的逃逸性能参数与无偏差工况的对比情况见表4。

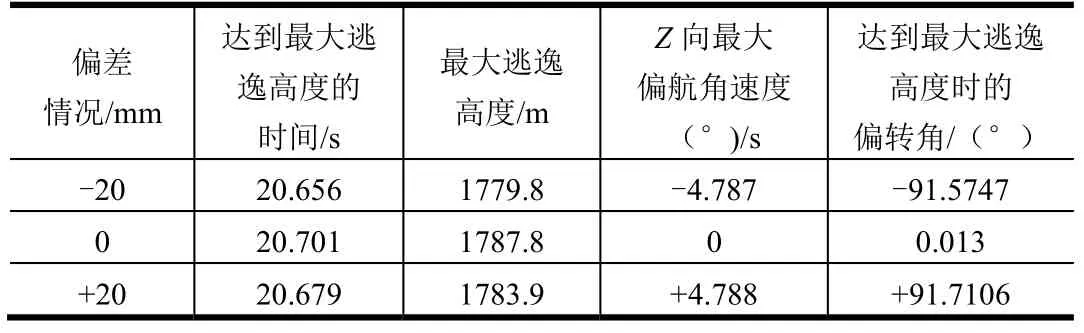
表4 横向质心偏差工况下逃逸性能参数对比Tab.4 Comparison of Escape Performance Parameters under the Condition of Transverse Centroid Deviation

通过仿真分析表明，逃逸飞行器横向质心偏差对最大逃逸高度影响不明显，但对逃逸飞行器的姿态特征有较大影响。当逃逸飞行器的横向质心偏差从 -20 mm到+20 mm变化时，达到最大逃逸高度时逃逸飞行器的偏转角从-91.5747°至+91.7106°变化，因此推力矢量调整工作中横向质心偏差会导致逃逸飞行器姿态角放大，且在逃逸飞行过程中姿态变化较快，应严格控制横向质心偏差。

5 结 论

针对有塔逃逸飞行器质量质心特性不能实测获得的实际情况，本文对长征二号F载人运载火箭推力矢量调整过程中存在的质量偏差、质心位置偏差对有塔逃逸飞行器的安全性影响进行了分析，通过建立理论模型和仿真分析模型，得到如下结论：

a）有塔逃逸飞行器作为一种无控飞行器，必须开展推力矢量调整工作，否则逃逸过程中会发生翻滚，不满足安全逃逸要求。

b）推力矢量调整过程中质量特性偏差的影响对逃逸高度和飞行器姿态影响很小，可忽略不计。

c）推力矢量调整过程中纵向质心位置偏差会导致逃逸飞行器姿态角放大，但在逃逸飞行过程中姿态变化缓慢，不会引起逃逸飞行器的姿态急剧变化。

d）推力矢量调整过程中横向质心位置偏差会导致逃逸飞行器姿态角放大，且在逃逸飞行过程中姿态变化较快，应严格控制横向质心偏差。