基于改进型BP神经网络的随机车祸持续时间预测

姚 洁

(福州外语外贸学院， 福州 350202)

2020年，中国公路建设已达到300万km(含高速公路总建设达8.5万km)，位居世界第一。随着路网的高速发展，机动车数量的逐年增加，截至2020年中国民用汽车保有量已经达到26 150万辆。与此同时，交通事故频发成为广大群众密切关注的问题。对随机车祸处理周期也成为民众所关心的热点。目前，国内外学者也提出了多种随机车祸持续时间预测的算法模型。早期传统的统计方法有概率分布发[1]、回归分析法[2]和时间序列[3]等。Wang等[4]采用偏最小二乘法，通过最小化误差的平方和找到与车祸持续时间最为匹配的一组数据，建立了不同类型的随机车祸持续时间预判模型。马阿瑾[5]采用决策树法预测事故响应时间和事故清除时间，再利用交通波理论和排队论估算无干涉和干涉条件下交通恢复时间，在此基础上得到总的随机车祸持续时间，构建高速公路交通事故持续时间预测的分阶段模型。传统的方法虽然给随机车祸持续时间预测奠定了理论研究基础，但其预测范围和精度不够理想。随着人工智能的发展，越来越多的模型被用于随机车祸持续时间预测中，如支持向量机[6-7]、人工神经网络[8-9]。赵金元等[10]、朱秋辰[11]分别采用BP神经网络算法、支持向量机以及随机森林算法构建了大货车高频次行驶路线短时事故预测模型。但是复杂的模型算法在增加预测精度的同时却忽略了时效性，而精准、实时预测随机车祸持续时间才能给事故处理起到决策意义。

综上所述，本文对现有随机车祸持续时间预测算法进行改进，将因子分析和BP神经网络算法相结合。利用因子分析减少随机车祸原因维度，再将提取的公共因子作为输入层参数，利用BP神经网络高度自学习、自适应的能力，可高精度逼近任何非线性连续函数，提高模型的迭代速度。

1 随机车祸特征分析

随机车祸时间跨度包含从交通事故发生到路况恢复的全过程。主要有事故发现、响应、清除和恢复4个阶段。具体如图1所示。本文所涉及的公路随机车祸仅仅指造成公路交通状态受堵滞的交通事故，不考虑公共建设的非紧急事件的影响，如公路维修、基础建设、道路改造等。

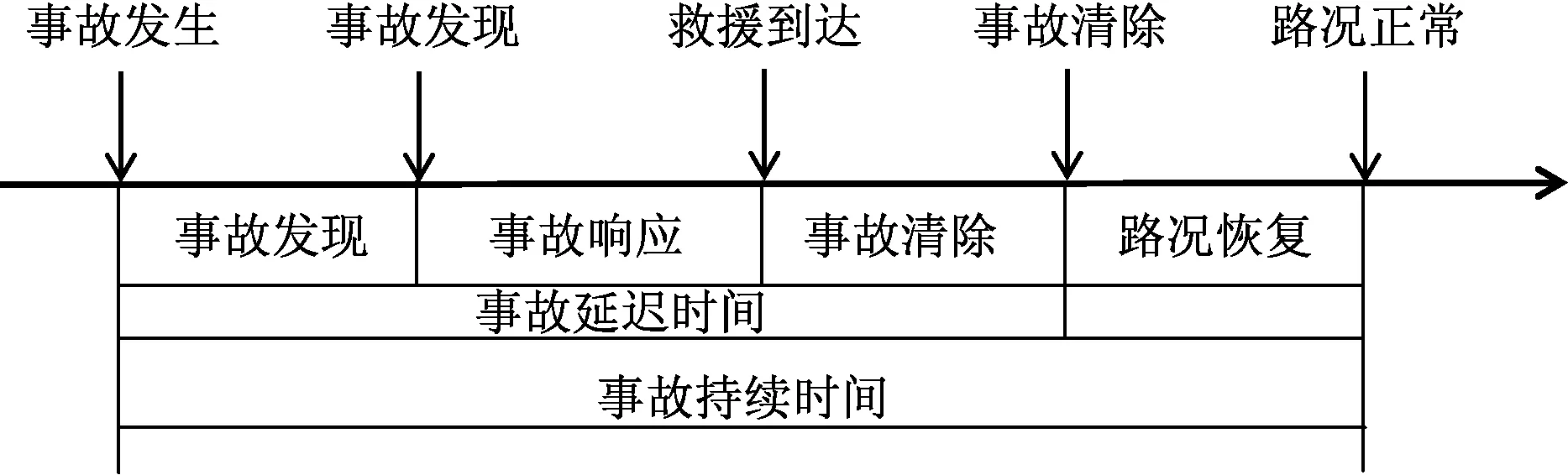
图1 公路随机车祸持续时间分布

由图1可知，事故发现、事故响应、事故清除构成了事故延迟时间，主要受事故检测和事故清除能力的影响，属于可控变量。路况恢复主要受事故延迟时间公路交通状态、事故等级、自然因素等诸多因素制约，属于不可控变量。综上所述，本文主要从公路随机车祸中的时间信息、路段信息、事故信息、环境信息这4个属性考虑，归纳了随机车祸的总量、时间、环境、地点、车祸类型、车辆信息、事故原因、损失情况等影响因子。

2 随机车祸持续时间预测模型

2.1 基于因子分析的随机车祸影响因素

由英国心理学家C.E.斯皮尔曼提出的因子分析，其主要思想即从变量群中提取公因子。通过变量群之间协方差矩阵的变量内部依赖关系，获得少数几个隐藏的“抽象”的变量来代表变量群。这几个“抽象”的变量被称之为“因子”，各个因子之间互不相关，所有变量都可表示成公共因子的线性组合，是一种降维、简化数据的技术。

本文将公路随机车祸持续时间的影响因素设为初始变量，采用R型因子分析法降维，确定较少的公共因子，并用公共因子代替所有变量去分析，以便提高运算效率。其计算过程如下：

1)选择分析的原始变量，建立因子模型。设p为影响因素个数，m为公共因子个数，X为影响因素矩阵，F为公共因子矩阵，A称为因子载荷矩阵，ε为特殊因子矩阵。研究表明，变量之间存在内部依赖关系，潜在的假想变量加上随机变量的线性组合，即

X=AF+ε

(1)

式中：

2)因子载荷矩阵求解。因子载荷反映了第i个变量与第j个公共因子的相关系数，绝对值越大，相关的密切度也就越高。这里采用主成分分析法对相关系数矩阵进行操作，求出特征向量、特征值和主成分贡献率。

(2)

(3)

式中：λ为样本相关系数矩阵的特征值；e为相应的标准正交化特征向量。

3)因子载荷矩阵的旋转。为了便于对主因子进行专业诠释，避免出现多个变量均在同一因子上出现较大因子载荷，或者一个变量在多个因子上具有较高载荷，而造成对因子难解释或命名，使用旋转后的因子载荷尽可能地拉开每一列元素的距离，使其两极化。同时每一个变量也只在少数几个主因子上具有较高载荷，便于因子分析和命名。设Q为m阶正交矩阵，令B=AQ，则

BBT=AAT

(4)

4)建立因子得分模型。因子得分模式是将主因子表示为原始变量的线性组合。采用回归法对因子得分进行估计，将影响因素矩阵X表示为公共因子矩阵F的线性组合，将问题转化为低维空间，得到公因子矩阵F。

(5)

式中，(bij)n×m为因子得分系数。

2.2 BP神经网络算法的随机车祸持续时间预测

BP神经网络模仿生物神经网络，神经网络中的神经元呈现不规则的网状模型，当某个神经元“兴奋”时，就会向下一级神经元发送化学物质，来改变这些神经元的电位。若某一神经元电位超过一定阈值则被激活，否则不被激活。这个过程称之为误差逆传播算法。BP神经网络通过多次训练得到的预测结果与实际结果进行误差分析，从而修改其权值和阈值，最终得到输出和实际结果近似的模型。推导中采用的这种算法叫作多层前馈神经网络。其拓扑结构如图2所示[12]。

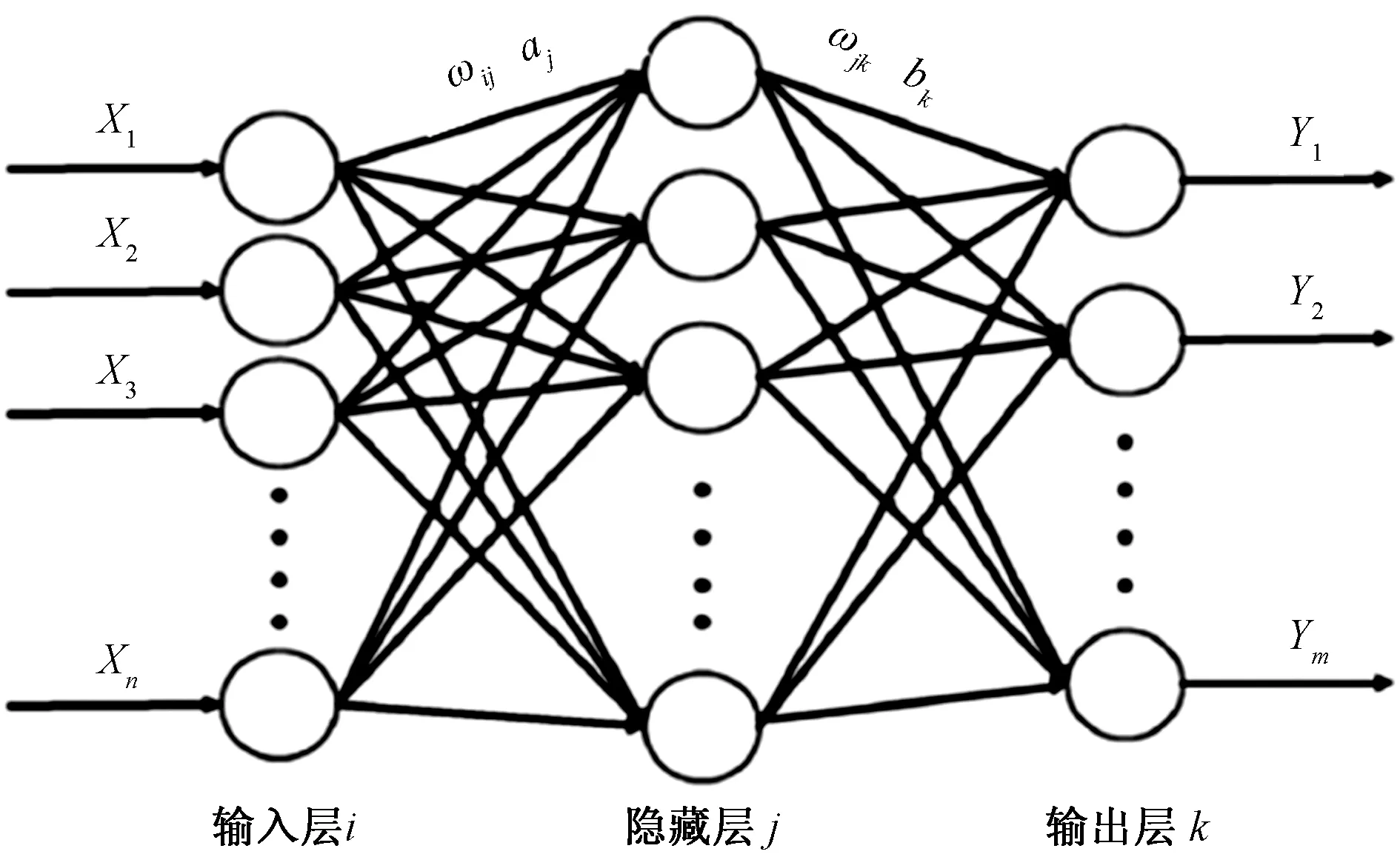
图2 BP神经网络拓扑结构

图2中采用的是简单的三层神经网络，X1，X2，X3，…，Xn为输入BP神经网络输入层的值；Y1，Y2，Y3，…，Ym是输出成输出的预测值；ωij为输入层第i个神经元与隐藏层第j个神经元之间的连接权值；ωjk为隐藏层第j个神经元与输出成第k个神经元之间的连接权值；aj为输出入层第j个神经元的阈值；bk为隐藏层第k个神经元的阈值。其训练过程如下：

1)计算神经网络输出值。

(6)

式中，Hj表示第j个隐含层的输出。

2)计算预测误差。

ek=Yk-Ok

(7)

3)修正连接权值。

(8)

式中，η为神经网络学习速率。

4)BP神经网络各节点阈值修正。

(9)

3 基于改进型BP神经网络的随机车祸持续时间预测模型

本文选取福银高速2015年1月至2020年12月的交通事故数据，共计20 518条作为数据源。首先采用因子分析方法确定降低随机车祸的影响因素维度。再利用BP神经网络模型预测车祸持续时间。将模型嵌入交通监控系统，有利于职能部门对事故的调度处理，有利于道路拥堵的控制。

3.1 因子分析法

本文主要从公路随机车祸中的时间信息、路段信息、事故信息、环境信息这4个属性考虑，提取了11个随机车祸持续时间的影响因素。具体见表1。

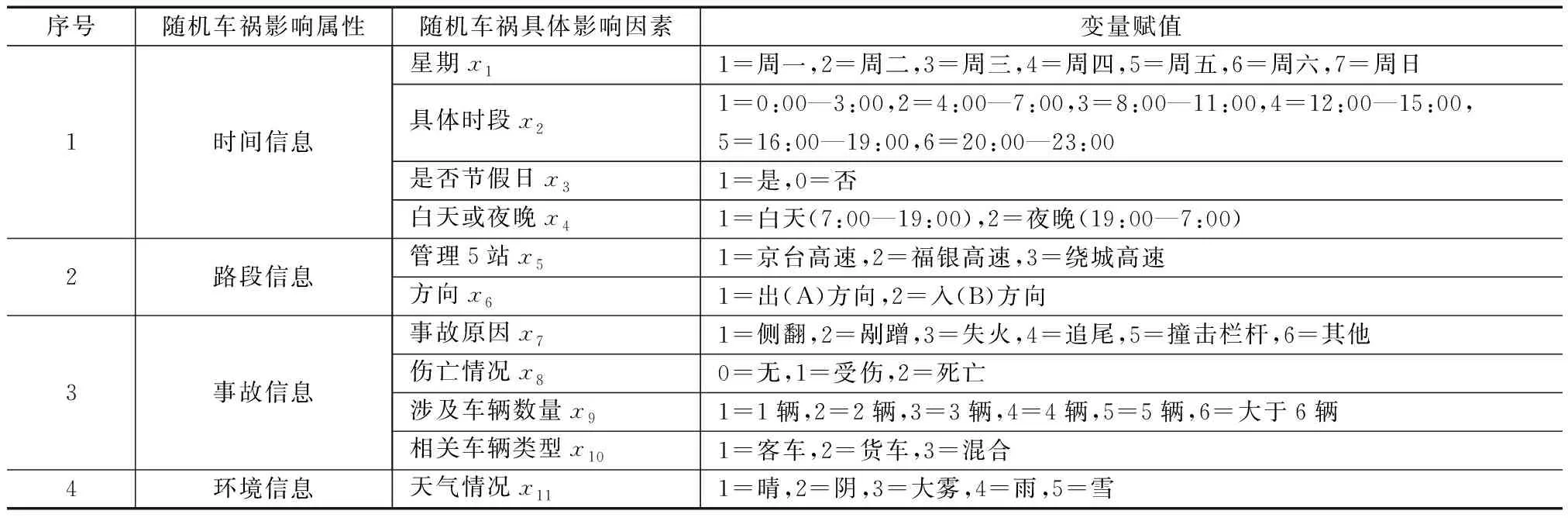
表1 随机车祸持续时间的影响因素

1)相关性分析。首先，通过SPSS对随机车祸的影响因子进行降维。表2为Bartlett检验结果，可见KMO大于0.5可做因子分析，Sig值小于0.05认为变量之间具有较强的相关性。

表2 Bartlett和KMO检验结果

2)提取公共因子，计算因子得分。根据其相关系数矩阵(协方差矩阵的标准化)提取公共因子，见表3。其中，相关系数矩阵取大于0.6即可，若大于0.7表示原始变量能被公因子解释得很合理。接着，使用总方差来解释因子对于原始变量的贡献率。如图3所示，按照特征根大于1的默认指标从中提取了4个公因子，并对其进行标准处理后作为BP神经网络预测的输入数据。

表3 公因子方差

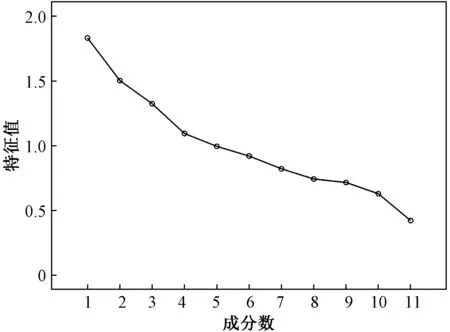
图3 碎石图

3.2 BP神经网络的构建

BP神经网络采用三层结构，其中将经过上述因子分析得到的4个影响随机车祸持续时间的公共因子作为输入层参数。隐藏层神经元个数的选取需要既保障模型的收敛性又能降低预测速度。因此，在满足模型精度的前提下，尽可能地简单化模型，本文通过下面公式预估神经元个数l。

(10)

式中：a为输入神经元个数；b为输出神经元个数；c为经验值(取值为0～10)。通过优化算法，隐藏层神经元个数按经验取值为9，BP神经网络预测效果最好。综上所述，BP神经网络模型结构为4-9-1。

3.3 公路随机车祸持续时间预测

采用MATLAB 环境进行仿真(目标误差为0.01，显示中间结果的周期为50，最大迭代次数为500，学习率为0.01)。其流程如图4所示，经过训练后拟合度如图5所示，经过每一次训练，误差随之不断减少，当训练到第12次时，效果最佳，误差最接近目标且收敛快。因此BP神经网络模型结构为4-9-1是合理的。

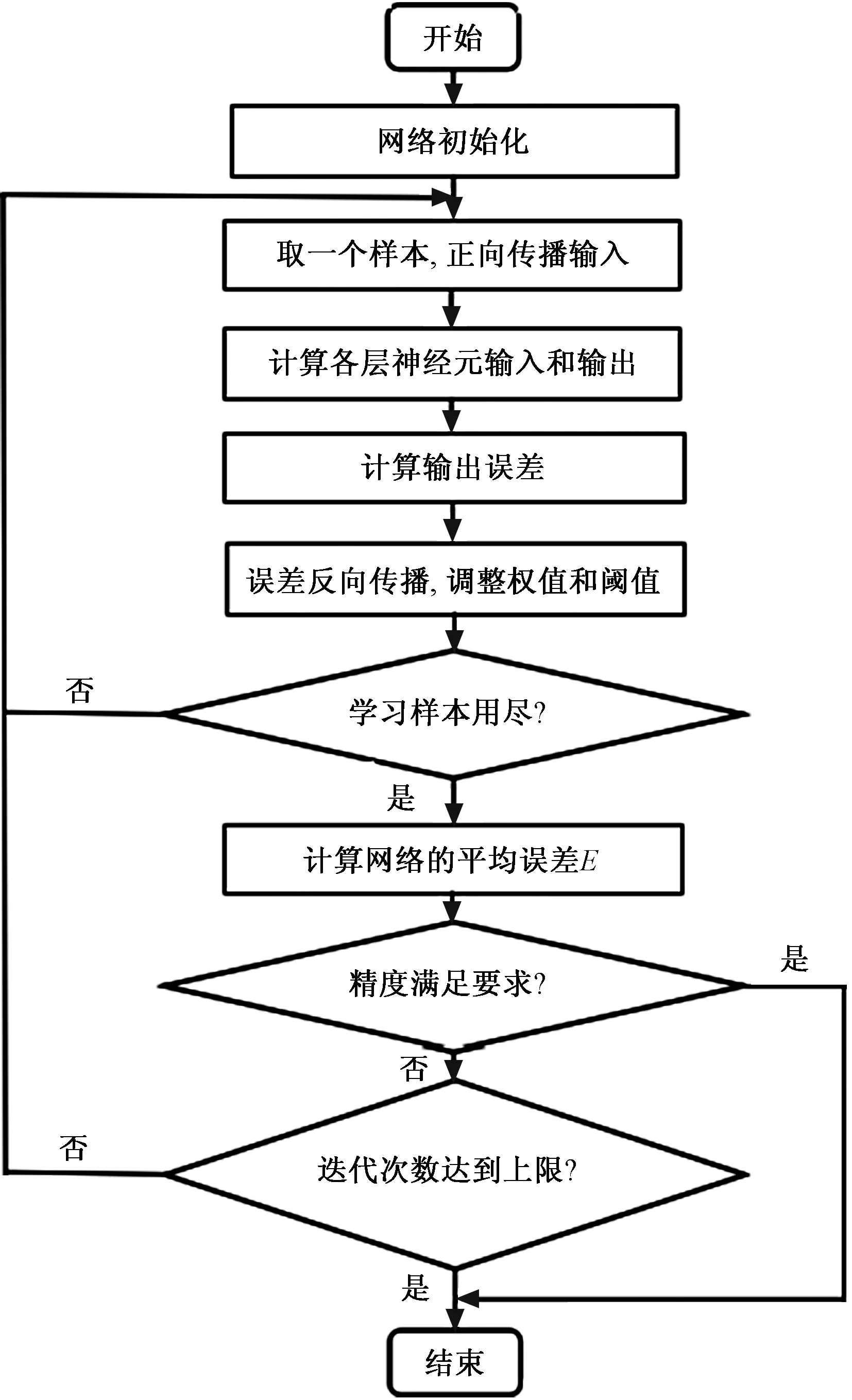
图4 BP神经网络预测流程

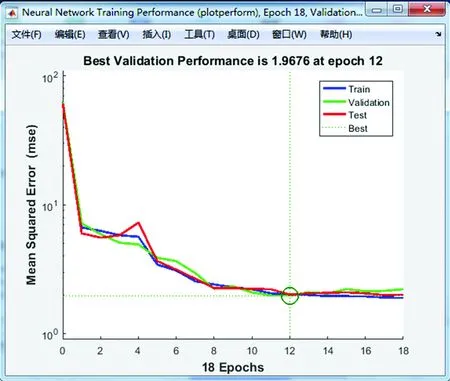
在训练迭代12次后达到最佳值为1.967 6图5 拟合曲线

4 结论

通过因子分析与BP神经网络相结合对公路交通事故持续时间进行预测，通过因子分析对影响因素进行降维处理，减少了原有神经网络中隐含层及输入节点数量，简化了模型的网络结构，提高了模型的预测速度和收敛性。同时在预测精准性上优于传统的支持向量机制和回归模型。在缩短预测时间的同时，对实际工作中快速进行车祸事故处理具有指导性作用。