NTLBO算法优化ELM的SOC预测方法

胡 坚， 刘 超

(1.浙江经贸职业技术学院 信息技术系, 浙江 杭州 310018；2.贵州航天电器股份有限公司, 贵州 贵阳 550009)

1 引 言

锂电池是一种具有高能量密度、低记忆效应、轻量化等优点的清洁能源。荷电状态(state of charge, SOC)是用于表示电池剩余容量的主要参数，通常估计获得[1]。一个不准确的估计将导致电池过充、深度放电，加剧电池寿命的减少，且有引入电池高危运行的风险。因此，锂电池SOC准确预测具有实际的研究与应用价值[2]。

不同的电池荷电状态预测方法具有不同的预测结果和不一致的准确性。开路电压法是一种离线SOC估计方法，不便实时预测;卡尔曼滤波估计[3]和非线性回归也是常用的SOC预测方法;文献[4]采用一种最优自适应增益非线性观测器来预测SOC;范兴明等采用改进的增量学习相关向量机对锂电池荷电状态进行在线预测，并获得通用性较强的预测模型[5];王晓兰等[6]通过采用极限学习机算法建立SOC在线估计模型，取得了满足应用需求的估计精度。

极限学习机(extreme learning machine, ELM)由于在训练过程中不需调整模型参数，以更小的权值范数对数据进行快速训练即可获得更小的训练误差[7]，因此，在工程实践中应用广泛。基于此，本文采用ELM算法建立锂电池SOC预测模型。为改善ELM模型的预测精度、降低模型参数随机性对SOC预测精度的影响，提出采用一种新型的教与学优化(new teaching-learning-based optimization, NTLBO)算法[8]与ELM结合，通过NTLBO算法对ELM随机模型参数进行优化调整,建立SOC与其强相关性参数如电池电压、电流之间的非线性模型。将提出的NTLBO-ELM模型应用于某型号锂电池SOC的预测，仿真结果表明该模型能够对锂电池的SOC做出更加准确的预测，具有应用推广价值。

2 极限学习机

ELM是一种基于前馈型单隐层神经网络的监督学习算法。与传统学习算法不同，ELM提供了非常快的学习速度和简单的学习过程，并具有良好的模型性能。若输入层有n个神经元、隐藏层有L个神经元、输出层有m个神经元。假设Q个训练样本集{(xi,yi)}，其中输入数据为xi=[xi1,xi2,…,xin]T∈Rn，输出数据为yi=[yi1,yi2,…,yim]T∈Rm，ELM模型的激活函数为g(x)，其数学模型描述为[9, 10]：

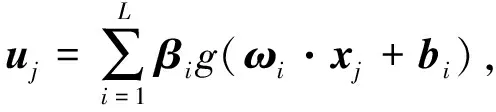
j=1,2,…,Q

(1)

式中:ωi=[ωi1,ωi1,…,ωin]为输入权值矩阵，用于连接第i个隐层神经元与输入层神经元的权值向量；bi是第i个隐层神经元的阈值；xj=[x1j,x2j,…,xnj]T，βi=[β1,β2,…,βm]是输出权值向量；uj=[u1j,u2j,…,umj]T为ELM模型的输出。

上式可简化为：

Hβ=UT

(2)

式中:U=[u1,u2,…,uQ]，UT是U的转置矩阵；β=[β1,β2,…,βL]；H称为隐层输出矩阵。

ELM的训练目标是最小化训练误差，当激活函数是无限可微且H唯一确定，ELM训练等效于通过求解式(3)的最小二乘解得到输出权值β：

(3)

求解β：

(4)

式中:H+是矩阵H的Moore-Penrose广义逆。

3 新型教与学优化算法

3.1 标准TLBO算法

教与学优化算法(TLBO)是一种受启发于教学现象的群智能优化算法[11]。TLBO包括教学阶段和学习阶段两种策略。教师在教学阶段向学生提供知识，学生在学习阶段通过相互交互进行学习。教学阶段通过式(5)策略期望其他学生能直接从老师获得知识[12]。

(5)

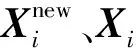
学习阶段，一个候选解Xi通过一个随机学习者Xj进行评估，描述如下：

(6)

式中:i≠j;f为适应度函数。

3.2 新型TLBO算法

TLBO算法在教学阶段具有良好的开发性能，而学习阶段则在当前位置的有限范围内进行探索，因而，TLBO算法的全局搜索与局部搜索协调不足，易陷入局部最优。为改善TLBO算法的全局优化性能，提出一种新型的TLBO算法:采用Logistics搜索策略对种群中排名前10%的个体进行更新，增强种群的多样性和跳出局部最优的能力。Logistics搜索策略描述为[13]：

Zi(t+1)=μ·Zi(t)·[1-Zi(t)]

t∈[0,…，tmax-1]

(7)

式中：t为当前混沌搜索次数、tmax为最大混沌搜索次数；Zi(t)为混沌变量，取值区间为[0, 1]；μ为控制参数，且μ∈[0,4],当μ=4时，Logistics映射将处于完全混沌状态[13,14]。

为了增强算法跳出局部最优的能力，将Logistics混沌引入TLBO中(记为NTLBO)，描述如下：

1)针对极小化问题,种群适应度计算，并降序排序；

2)选择排列前10%的个体，构成集合{Pi}，其中i取值范围为[1, round(0.1×N)]，元素Pi分别对应种群中适应度前10%的个体；

3)将Pi按式(8)进行归一化操作：

(8)

式中:Z(0)为元素Pi初始混沌变量，Z(0)∈[0,1]；U和L分别为优化问题的上、下限。

4)利用式(7)对Pi进行混沌操作，产生混沌个体Zi(t+1)；

5)通过式(9)将Zi(t+1)映射到解空间，得到Pi的对应混沌个体Pc,i：

Pc,i=Zi(t+1)×(U-L)+L

(9)

6)通过贪婪选择策略确定第i个个体Xi的位置，针对极小化问题：

(10)

基于混沌的随机性和遍历性将有效增强算法跳出局部最优的能力。

4 NTLBO-ELM预测模型

由于ELM的输入权值和隐含层阈值是随机的，导致在工程实际应用中存在泛化能力弱、预测精度低等问题。因此，本文研究应用新型教与学优化算法优化ELM模型，记为NTLBO-ELM。NTLBO主要对ELM模型的输入权值和隐含层阈值进行优化选择，以提高ELM的学习性能。NTLBO-ELM算法流程如图1所示。

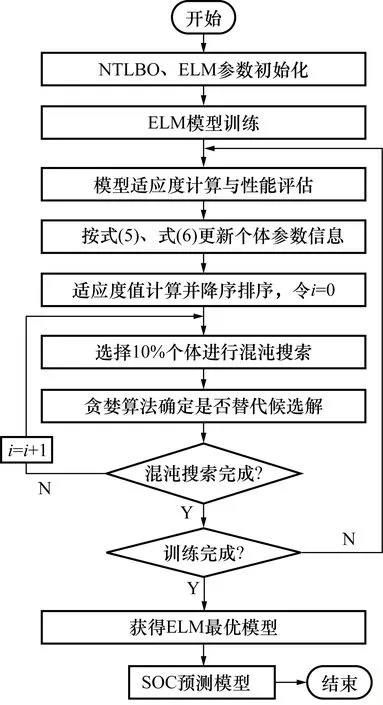
图1 ECTLBO-ELM模型训练流程图

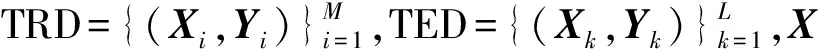
(11)

式中：ELM(Xk)为ELM模型预测值。

NTLBO-ELM核心思想是通过NTLBO算法来解决ELM模型中超参数优化问题，即将TRD数据作为ELM的输入训练模型，利用TED数据进行模型评估，将预测值与真实值作对比，NTLBO算法通过极小化适应度函数来达到调整最佳模型参数的目的。

5 SOC预测实验与结果分析

以某10 A·h的锰酸锂离子电池为试验对象，采用放电仪和综合测试仪在恒温箱中进行不同放电倍率的恒流放电实验。影响SOC的最主要2个参数是电池电压与电流，实验选用同一节锂离子电池，让其分别在3种不同的放电倍率下进行恒流放电，放电倍率为1C,6C和9C[15]。实验数据见表1所示，每种放电倍率下各25组数据。为了验证NTLBO-ELM算法的有效性，从每种放电倍率下随机选择22组数据(共66组数据)作为训练集(TRD)，余下的9组数据为测试集(TED)。

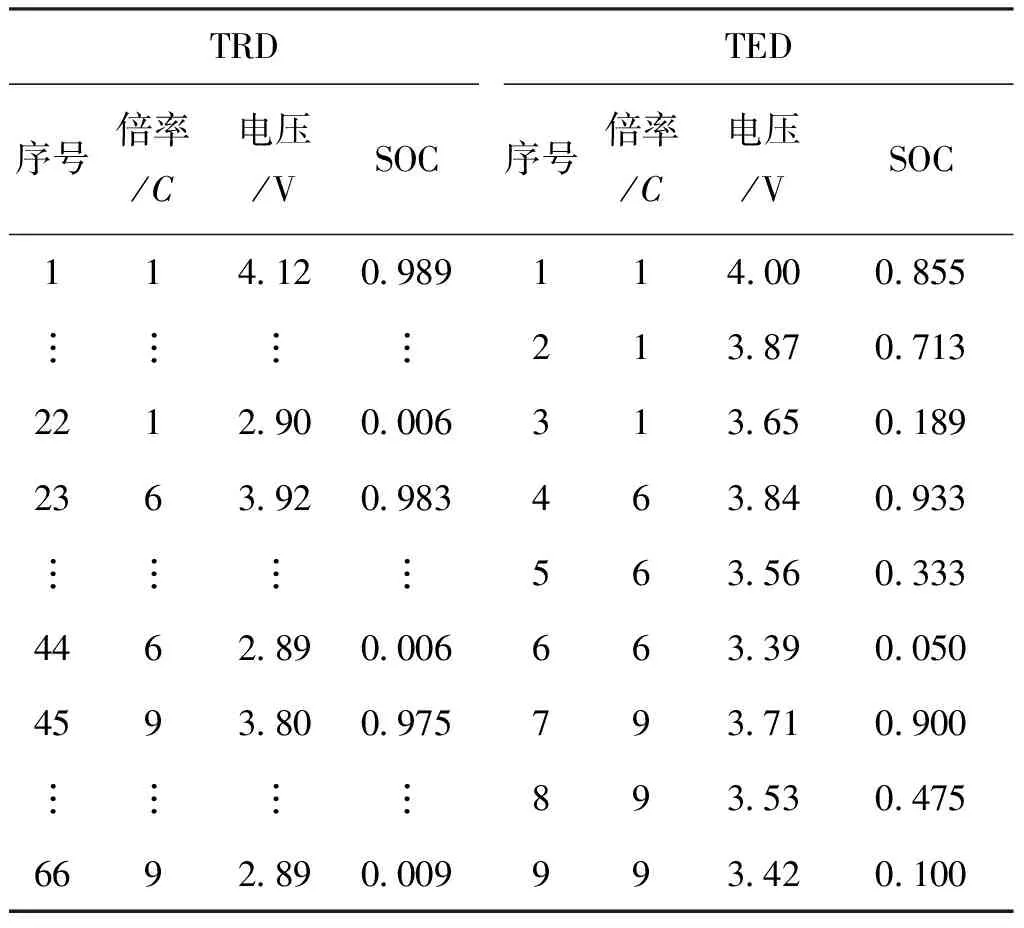
表1 SOC样本

图2给出了NTLBO-ELM模型针对训练集的预测结果，3条预测曲线显示预测值与真实值几乎完全重合，表现出良好的预测性能。为验证NTLBO-ELM模型泛化能力，对TED数据集进行测试验证，并将其预测结果与TLBO-ELM、ELM和BP模型预测结果进行对比，见图3所示。由图3可以看出:BP模型和ELM模型SOC预测值与真实值整体上变化趋势一致，均能一定程度上对SOC进行可靠预测;NTLBO-ELM、TLBO-ELM的预测效果明显优于ELM模型，尤其是NTLBO-ELM模型，其SOC预测值与真实值咬合得更加紧密。

图2 NTLBO-ELM训练集预测结果

图3 测试集预测结果

表2给出了4种模型的性能指标，从中可见:4种模型的绝对误差均值分别为0.011，0.034，0.078，0.050，尽管值都很小，但是ELM的误差是NTLBO-ELM的7倍；此外，NTLBO-ELM模型的相对误差均值为最小，进一步验证了NTLBO-ELM的SOC预测模型的整体性能更好。综上所述，NTLBO-ELM模型具有更强的泛化能力。

表2 性能指标

6 结 论

本文主要研究基于极限学习机(ELM)的锂电池荷电状态(SOC)的预测问题。准确的SOC预测能够有效防止电池过度放电，并延长电池的使用寿命。为解决ELM预测性能受模型超参数的影响，采用新型NTLBO算法进行ELM模型输入权值和隐层阈值的优化调整。在10 A·h的锰酸锂离子电池的SOC预测实验中，相比于其余3种模型，NTLBO-ELM模型更有效地预测锂电池的SOC，反映NTLBO算法能够有效优化ELM模型参数，避免超参数选择的盲目性，可为锂离子电池SOC的预测与应用提供参考。