OVMD-MPE群稀疏全变分去噪算法研究

陈维兴， 孙习习

(中国民航大学，天津 300300)

1 引 言

滚动轴承作为旋转机械的重要连接件，其运行状态直接影响机械系统的整体性能和寿命[1]。由传感器采集的振动信号通常混合强背景噪声干扰，无法直接实现轴承早期故障诊断。因此，对振动信号进行有效的去噪处理具有重大意义。信号的分解和滤波是非线性振动信号去噪的关键。针对信号的分解问题，变分模态分解(variational modal decomposition，VMD)是Dragomiretskiy和Zosso在经验模态分解(empirical modal decomposition，EMD)的基础上提出的自适应信号分解方法，抗干扰能力强，鲁棒性好，在信号处理领域具有明显优势[2～6]。基于VMD的信号分解取决于分解参数的选择，合适的目标函数和优化算法是提高信号分解效率和精度的关键。刘尚坤等[7]提出了一种基于互信息优化的VMD算法，但只考虑了模态数对分解结果的影响，分解精度不高。郑小霞等[8]利用粒子群优化算法寻找VMD的最优参数，收敛速度较慢，容易陷入局部最优。多尺度排列熵(multi-scale permutation entropy，MPE)作为描述时间序列复杂性的统计指标[9]。陈东宁等[10]将VMD和MPE结合，利用MPE量化VMD分解后各分量的特征信息，故障识别效果良好。针对信号的滤波问题，全变分去噪(total variational denoising，TVD)算法是一种基于最优问题的信号滤波方法[11]，最早应用于图像去噪领域[12，13]，目前在一维信号处理中得到广泛应用。Yang等[14]利用非凸罚函数构造二阶TVD算法，提高了对振动信号的降噪效果。朱丹宸等[15]通过二阶TVD处理振动信号，调制信号双谱分析故障特征，实现轴承故障诊断，但TVD滤波过程中受阶梯伪影干扰，降噪效果不佳。陈剑等[16]针对变工况条件下轴承故障数据无法大量获取以及诊断困难的问题，提出了基于变分模态分解和卷积神经网络的轴承故障诊断方法，使用稳态工况获取的数据训练，能对变工况下的数据实现有效诊断。

振动信号去噪是实现非线性非平稳混合信号降噪的过程。为了避免人为因素的干扰，本文采用VMD和MPE结合处理信号，引入蚱蜢优化算法(grasshopper optimization algorithm，GOA)以能量损失系数为目标函数改进VMD，借助MPE分离出噪声主导分量，GSTVD算法被用于滤除噪声分量的干扰，最后对滤波后的分量和其余分量通过VMD重构，完成信号去噪。该方法用于滚动轴承振动数据，取得了较好的去噪效果。

2 基本原理

2.1 VMD理论

VMD是一种基于构造和解决信号变分问题的新型多分量信号分解算法[17]。与EMD算法不同，每个模态分量均为有限带宽且围绕各自的中心频率。VMD通过搜索约束变分模型的最优解，将原始信号f(t)分解为K个具有稀疏特征的模态分量。具体约束变分问题为：

(1)

式中：{uk}={u1，…uk}和{ωk}={ω1，…，ωk}分别为第K个模态分量及其对应的中心频率。

为求得式(1)约束变分问题的最优解，引入式(2)的增广拉格朗日函数：

L({uk}，{ωk}，λ)

(2)

式中：α为惩罚因子；λ为拉格朗日乘子。

采用交替方向乘子法求解式(2)的鞍点即式(1)的最优解，在频域内迭代更新uk，ωk和λ，从而将原始信号分解得到K个模态分量。

2.2 MPE原理

MPE被定义为时间序列在不同尺度下的排列熵。对时间序列X={xn，n=1，2，…，N}进行粗粒化处理，得到粗粒化序列：

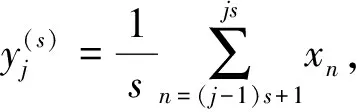
(3)

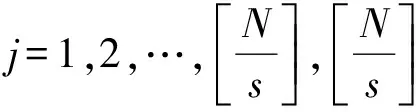
对每个粗粒化序列进行相空间重构，得到：

(4)

式中：m为嵌入维数；τ延迟时间；g为第g个重构分量，g=1，2，…，N-(m-1)τ。

将重构分量根据元素数值大小升序排列，得到一组符号序列S(r)=(g1，g2，…，gm)，其中r=1，2，…，R且R≤m!。计算每一种符号序列出现的概率Pr，求解每个粗粒化序列的排列熵并进行归一化处理，即可得时间序列的MPE值：

(5)

MPE表征时间序列的紊乱程度，MPE越小表明信号越规则，反之越复杂。一般的，MPE大于0.6的振动信号较紊乱，可能包含干扰成分。

2.3 群稀疏全变分去噪原理

假设，含有噪声的被测信号为：

y(n)=x(n)+w(n)

(6)

式中：y(n)为实测信号；x(n)为真实信号；w(n)为噪声信号。

利用一维TVD去噪模型求解优化问题，可以得到滤波信号：

(7)

式中：λ>0为正则化参数；F(x)为目标函数；φ(Dx)=‖Dx‖1表示惩罚函数。其中D为一阶差分矩阵。

(8)

对惩罚函数φ(u)进行群组优化，得到改进后的目标函数G(x，u)

(9)

式中：u=Dx为差分向量；c为常量。

为避免随迭代次数i的增加，导致信号保真度降低。这里引入矩阵引理同时利用MM算法求解式(9)，结果可以表示为：

(10)

因此，通过式(10)就可以实现信号的群稀疏全变分去噪。

3 OVMD-MPE群稀疏全变分去噪算法

3.1 优化VMD

在VMD算法中需要预先设定4个参数：模态分解数K、二次惩罚因子α、噪声容限τ和收敛准则容差ε。在实际的VMD分解过程中，后2个参数对分解效果影响较小，通常设为默认值τ=0，ε=10-7。而模态分解数影响信号分解的效率和精度，二次惩罚因子影响模态分量带宽的大小，因此，选择合适的[K，α]是提高VMD分解性能的关键。针对粒子群优化(particle swarm optimization，PSO)算法寻优效率低，容易陷入局部最优的问题，本文引入一种模拟蚱蜢群体觅食行为的新型群优化智能算法——蚱蜢优化算法[18]，以能量损失系数为适应度函数，利用GOA在多次迭代中寻找能量损失系数的最小值，从而确定VMD的最优参数[K，α]。

具体的VMD参数优化步骤如下所示：

Step1：初始化VMD参数{uk}，{ωk}，λ。设置GOA算法的种群数N，初始位置xi和最大迭代数L；

Step2：使用VMD分解信号，将能量损失系数作为适应函数并计算所有模态分量的适应值如式(11)所示

(11)

式中：∑uk为重构信号(k=1，2，…，K)；f为原信号；

Step3：蚱蜢算子通过式(12)更新自适应递减参数cn，确定当前位置：

(12)

式中l为当前迭代次数；

Step4：根据蚱蜢间的相互作用更新蚱蜢位置并改变适应值；

Step5：遍历空间内的所有蚱蜢算子更新个体最优目标位置和全局最小适应值；

Step6：如果达到最大迭代次数，则退出循环并输出目标位置和最小适应值对应的优化参数，否则返回Step2；

Step7：输出VMD最优参数结果。

3.2 振动信号降噪流程

OVMD-MPE群稀疏全变分去噪算法流程如图1所示。

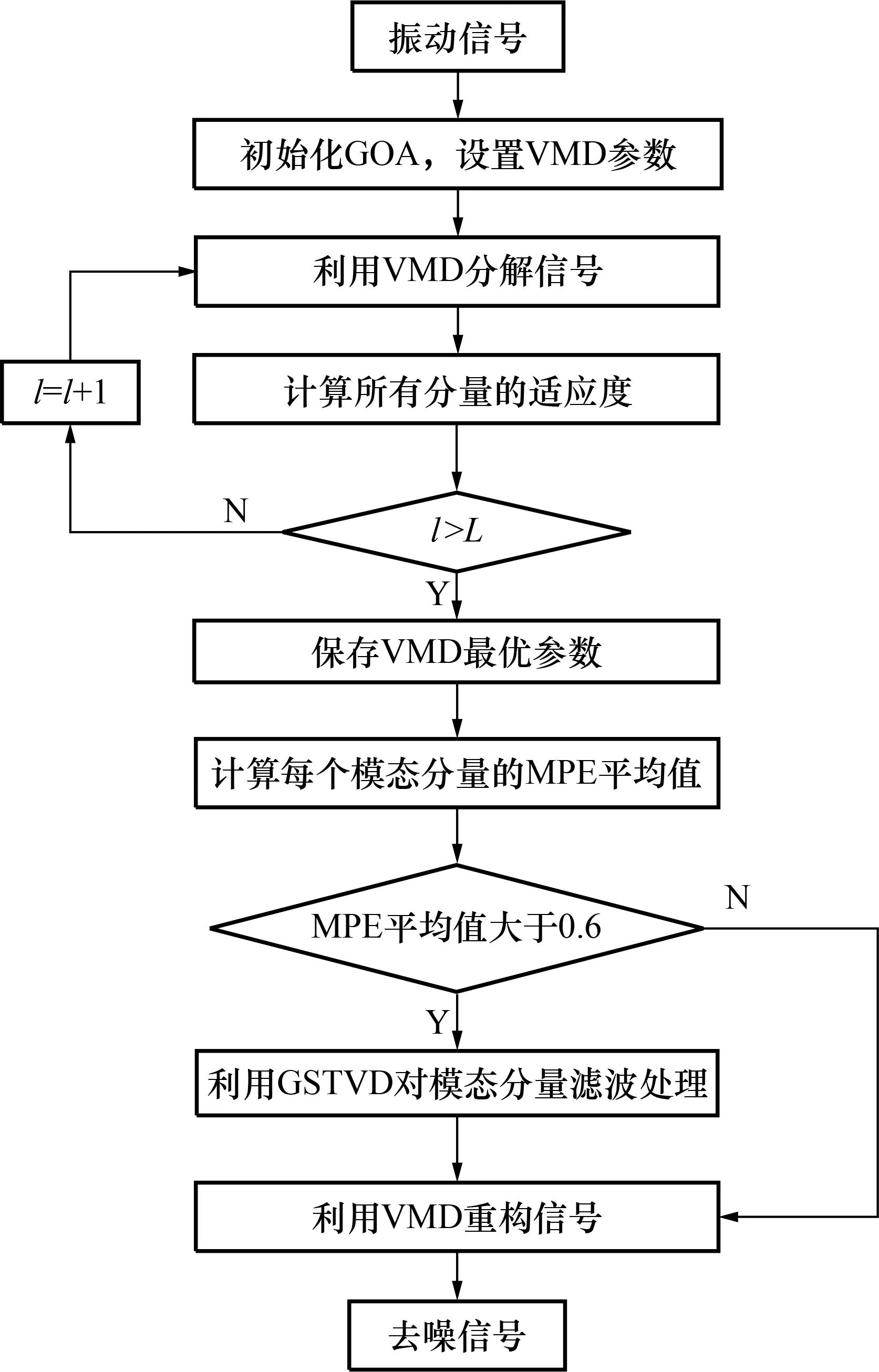
图1 OVMD-MPE群稀疏全变分去噪算法流程图

具体流程步骤如下：

Step1：利用GOA对VMD进行参数优化，确定最优模态分解数K和二次惩罚因子α；

Step2：通过参数优化后的VMD将振动信号分解为K个模态分量；

Step3：计算各模态分量的MPE平均值，根据MPE值是否大于0.6，判断各模态分量的含噪程度；

Step4：对噪声主导的模态分量进行GSTVD滤波处理；

Step5：通过VMD将Step4的结果与其它未进行降噪处理的有用分量相结合重构信号，得到去噪信号。

4 分析验证

4.1 仿真研究

为了验证本文提出的去噪算法，能在抑制噪声的同时保留原始信号的有效信息，这里利用周期性冲击信号模拟微弱的轴承内圈故障脉冲进行分析研究。所采用的模拟信号模型为：

(13)

式中：s(t)为周期性冲击信号；n(t)为零均值单位方差的高斯白噪声。给定内圈故障特征频率f=1/T=100Hz，转频f0=20Hz，系统的固有频率f1=3 000Hz。初始幅值A0，衰减系数B和第i次冲击的延迟时间τi分别设置为0.3，700，0.01 T。系统采样频率设为12kHz，数据长度为1 024。

为了模拟强背景噪声的工业现场，给故障冲击信号s(t)加入标准方差σ=0.7的高斯白噪声。图2为原始信号和噪声信号的时域波形，可以看出故障脉冲几乎被背景噪声完全淹没，周期性冲击成分难以体现，因此在故障诊断前有必要对信号进行去噪处理。

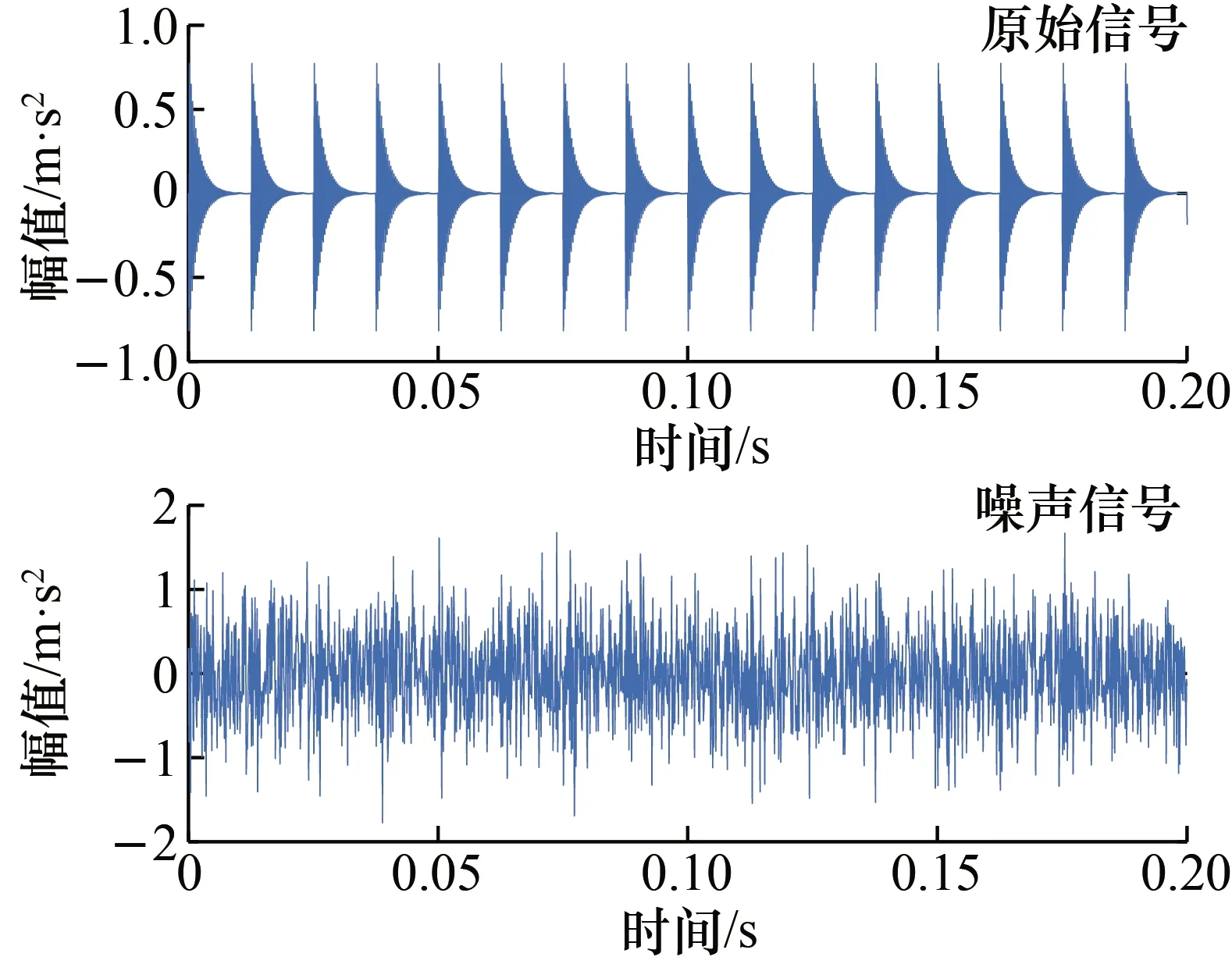
图2 模拟信号波形图

利用GOA算法对VMD参数进行优化，设定二次惩罚因子α的范围为[1 000，10 000]，模态分解数K的范围为[2，16]。为了比较本文VMD优化算法的分解性能，采用PSO算法与GOA算法以能量损失系数为适应度函数分别对VMD参数进行优化，设定初始种群大小为30，最大迭代次数为22。图3为VMD参数寻优过程中2种算法的收敛曲线，可以看出GOA在第3次迭代时取得最小能量损失系数为0.002 24，寻优结果为[K=4，α=1 035]；而PSO在第6次迭代时达到最小能量损失系数0.001 81，参数优化结果为[K=6，α=3 320]。与PSO算法相比，GOA具有更快的收敛速度和更低的能量损失系数。因此，选择基于GOA的VMD参数优化方法能够提高参数寻优效率，其搜索得到的最优参数为[K=4，α=1 035]。

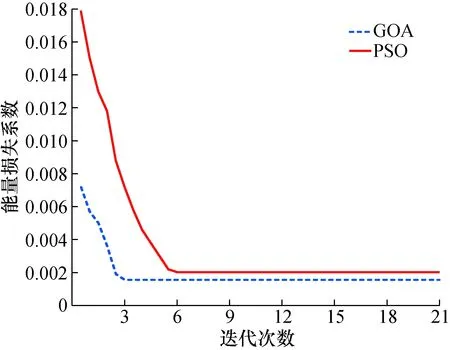
图3 模拟信号VMD参数优化的收敛曲线

根据寻优结果设定VMD的模态分解数为4，二次惩罚因子为1 035，模拟信号VMD分解结果如图4所示。结果表明：模拟信号分解后各模态分量中心频率相互独立，受噪声影响时域波形差异明显，无法具体判断各分量的含噪程度和是否存在虚假分量。

图4 模拟信号VMD分解结果

使用不同的尺度因子计算模拟信号各模态分量的MPE值，嵌入维数和最大尺度因子分别设置为m=6，s=15。图5为模拟信号各模态分量的MPE值分布结果，从图5中可以看出不同的模态分量对应的熵值不同，同一模态分量的熵值随尺度因子波动变化，这是因为不同模态分量的随机性和紊乱性有明显区别。因此，MPE值可以作为判断模态分量含噪程度的依据。

图5 模拟信号各模态分量的MPE

为避免尺度因子对熵值的影响，计算不同尺度因子下各模态分量的平均MPE值如表1所示。为避免信号特征信息的丢失，对于平均MPE值小于0.6的v4分量视为干净的分量，v1～v3模态分量受噪声主导，平均值均大于0.6，需要进一步的降噪处理。

表1 不同尺度因子时模拟信号各模态分量的平均MPE

将不同的信号分解算法为主导的去噪算法和不同的信号滤波算法为主导的去噪算法与本文的OVMD-MPE-GSTVD算法进行比较，小波阈值(WT)滤波采用小波基函数sym8生成得具有2尺度非抽取小波变换，迭代参数为0.4；设置TVD中正则化参数为0.7；GS-TVD设置组数k=3，正则化参数λ=0.7。图6为30次迭代实验下不同算法的去噪信号，结果表明，本文采用的OVMD-MPE-GSTVD具有更好的去噪效果，更低的均方根误差(RMSE)值表明信号平滑度更好。

图6 不同算法的模拟去噪信号

采用信噪比(SNR)评价不同算法的降噪能力，均方根误差(RMSE)评价去噪信号和真实信号的误差。对原始故障信号添加具有不同标准偏差的高斯噪声，测试不同噪声程度下不同算法的去噪性能。表2为去噪信号的平均信噪比值，结果表明：OVMD-MPE-GSTVD对于不同噪声偏差的信号处理效果优于其它算法，平均信噪比提高了3.3 dB。

表2 不同算法模拟去噪信号的平均信噪比

5.2 实验研究

为了验证本文方法对实测信号去噪的有效性，采用美国凯斯西储大学滚动轴承振动数据进行分析研究。实验所用驱动端轴承型号为6205-2RS IEM SKF深沟球轴承，采样频率为12 kHz。选用电机转速1 750 r/min，负载0.735 kW，损伤直径为0.178 mm的外圈故障振动信号。取1 024个数据点对轴承外圈故障信号进行时域分析，图7显示振动信号毛刺现象严重，周期性的故障冲击信号混有大量噪声，无法进一步判断对轴承故障状态。

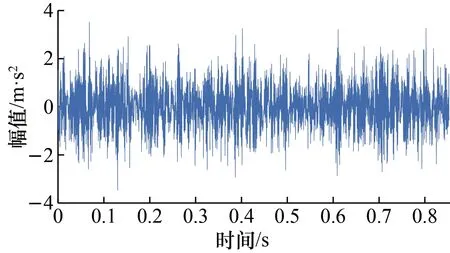
图7 外圈故障信号波形图

利用GOA算法和PSO算法分别对VMD输入参数进行优化，得到参数寻优过程的收敛曲线如图8所示。图8中在第5次迭代时GOA获得最小能量损失系数0.001 81，搜索得到最优参数为[K=4，α=1 027]；PSO算法在第7次迭代时达到最小能量损失系数0.002 04，得到最优参数[K=5，α=1 820]，GOA对VMD参数寻优效率优于PSO算法。因此，设置VMD的模态分解数K=4，二次惩罚因子α=1 027，对故障信号进行分解。

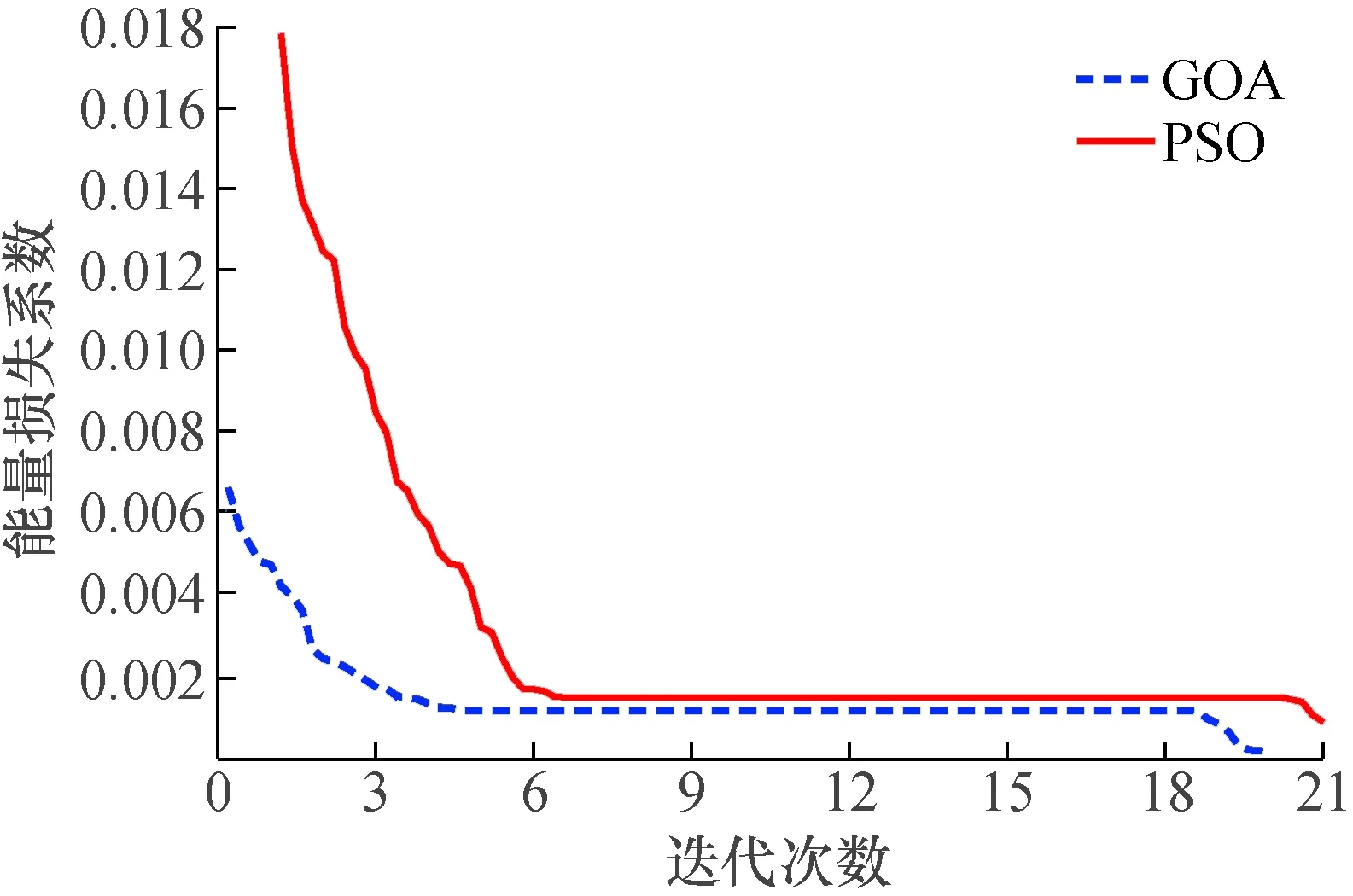
图8 外圈故障信号VMD参数优化的收敛曲线

图9为外圈故障信号VMD分解的波形图，从图中可以初步判断低频段v3和v4模态分量频率和时域幅值均较大，故障冲击特征明显，受噪声干扰较小；v1，v2处于中高频段时域波形幅值较小，可能包含虚假成分和大部分噪声扰动。

图9 外圈故障信号VMD分解结果

为进一步分析各模态分量的含噪情况，利用不同的尺度因子获得各模态分量的MPE值分布结果。设置嵌入维数m=6，最大尺度因子s=15，外圈故障信号各模态分量的MPE值随尺度因子变化如图10所示，从图中可以看出，各模态分量的熵值随尺度因子波动较大，v1～v2分量的熵值分布明显大于v3～v4分量，信号具有更多的噪声干扰。

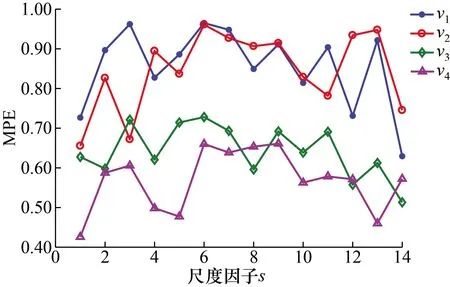
图10 外圈故障信号各模态分量的MPE分布

表3为外圈故障信号各模态分量的MPE平均值。结果表明，v1～v3分量包含噪声成分较多，信号随机性明显需要进行滤波处理；v4分量受噪声干扰小，具有信号故障特征信息，需要保留。

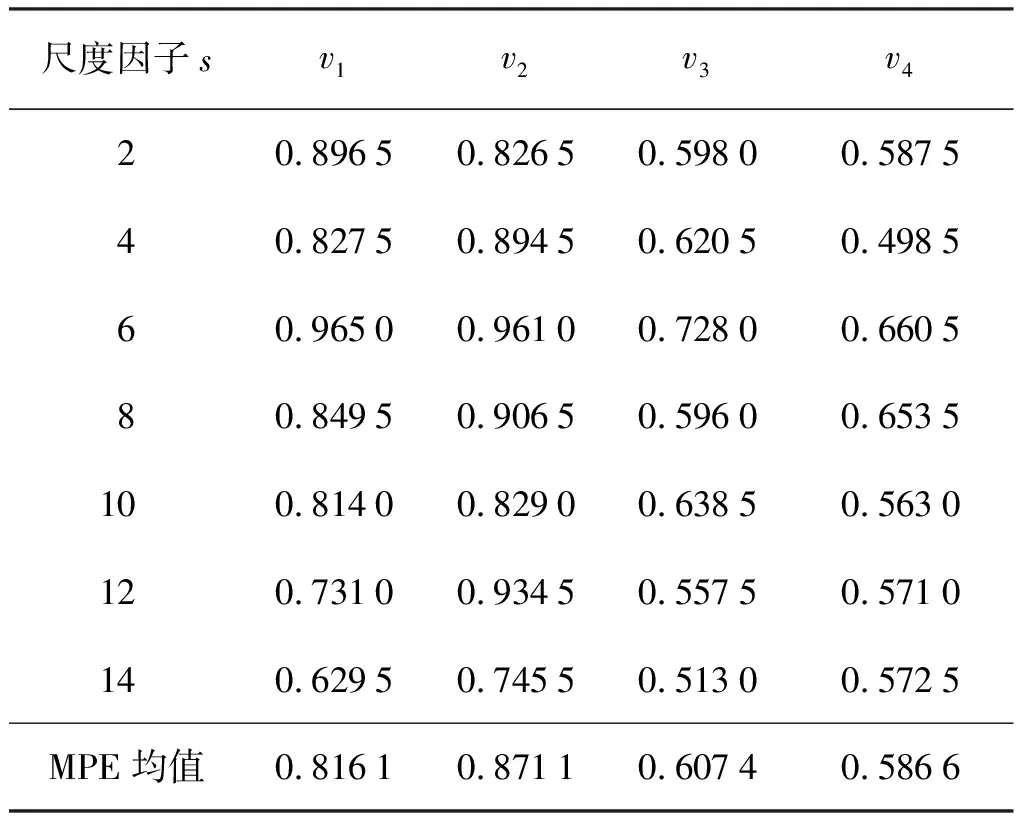
表3 不同尺度因子时外圈故障信号各模态分量的平均MPE

在不同的信号分解方法和滤波方法的基础上构造不同的去噪算法进行比较。图11为不同算法的去噪信号，结果表明：优化的VMD分解方法具有更低的RMSE，GSTVD与其它滤波方法相比，RMSE较低。因此，OVMD-MPE-GSTVD算法具有最好的去噪效果。

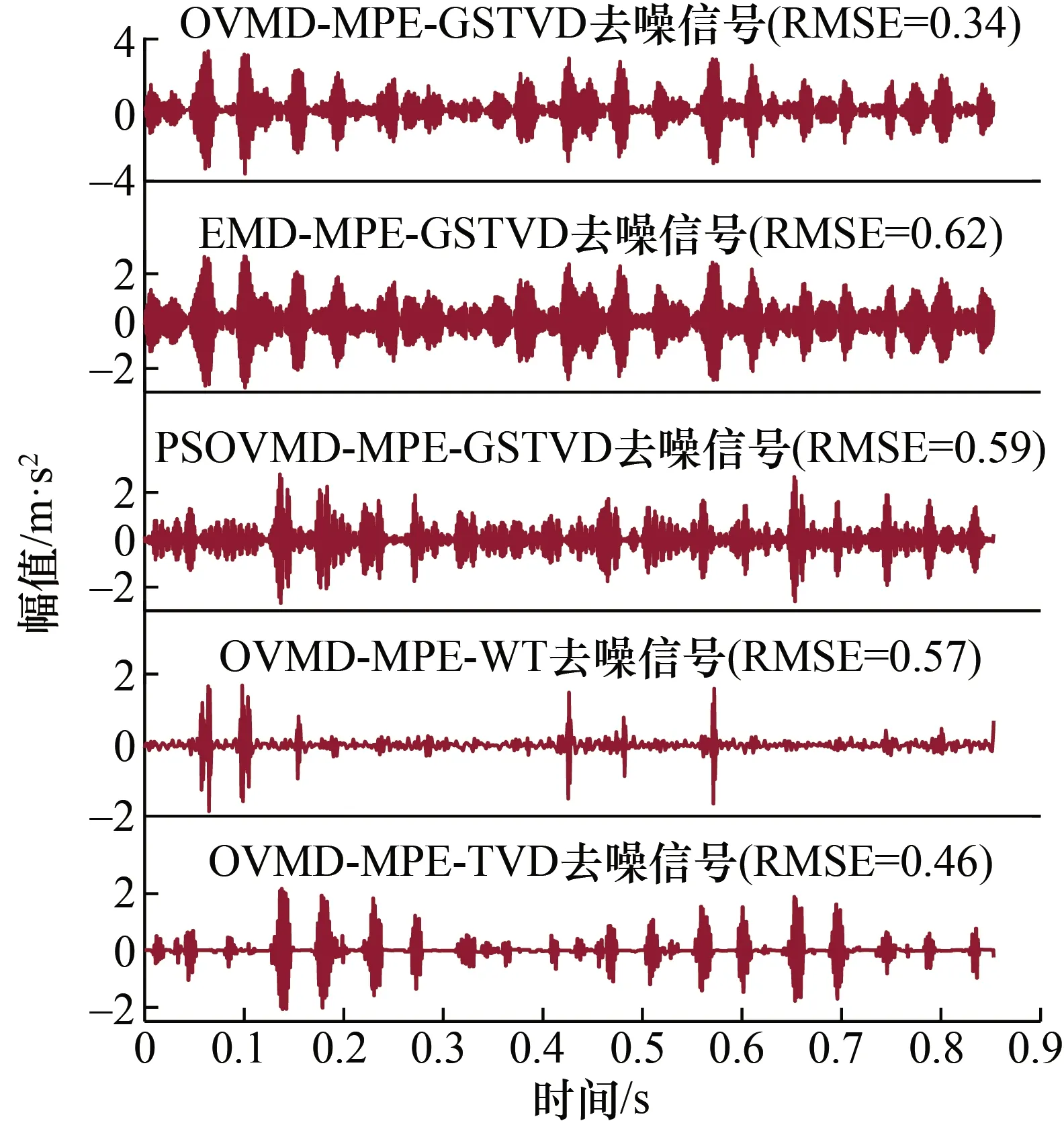
图11 不同算法的外圈故障去噪信号

5.3 去噪信号分类结果分析

利用一维CNN对5种去噪算法的模拟重构数据和轴承外圈重构数据进行故障诊断。一维CNN的结构及参数设置如图12所示，设置bachsize为64。

图12 一维CNN网络结构参数

为了验证不同去噪算法后续故障诊断的准确率，图13为不同去噪算法的重构数据通过一维CNN迭代60次后的准确率变化曲线。从图13可以看出，5种去噪算法测试集准确率在20次迭代后趋于稳定，其中OVMD-MPE-GSTVD算法曲线收敛速度最快，故障诊断准确率高于其它算法。因此，OVMD-MPE-GSTVD算法有利于提高轴承故障诊断的准确率，稳定性好。

图13 不同算法去噪信号的准确率变化曲线

5 结 论

本文提出了一种OVMD-MPE群稀疏全变分去噪算法，能够消除大部分强背景噪声分量，同时保留信号的有效特征信息，对模拟冲击信号和滚动轴承故障信号进行去噪，取得了较好的效果，提高了故障诊断的准确性。同时，介绍了一种VMD优化方法，通过提升参数优化收敛速度以适应实际振动数据需求。但本文尚未讨论多尺度排列熵的嵌入维数m、延迟时间τ对该算法去噪效果的影响，笔者将对其做进一步研究。