基于HIE-FDTD方法的太赫兹频段石墨烯吸收器的设计

韩晓冰 张辉 梁冰洋 周远国

（西安科技大学通信与信息工程学院，西安 710054）

引 言

石墨烯[1]是一种由单层碳原子构成的二维纳米材料. 由于其独特的六角形蜂巢晶格结构、动态可调性、低损耗性以及其在微波和太赫兹波段中独特的光学特性[2-3]，引起了科学界和工程界的广泛关注. 由于与传统贵金属相比石墨烯具有以上优点，近些年来学者们纷纷开展了微波波段以及太赫兹波段中石墨烯器件的研究工作.

在太赫兹器件中，吸收器对入射波的有效吸收非常重要. 一些由普通金属和介电材料组成的超表面吸收材料在制造后具有不可调性的固有缺陷. 然而，石墨烯具有极高的载流子迁移率以及其电导率取决于费米能级水平，而费米能级水平可以通过静电掺杂或化学掺杂来调节[4-5]. 因此，对石墨烯吸收器进行精确的建模和仿真具有较高实用价值.

众所周知，目前已有一些解析法和数值分析法用于模拟太赫兹频段的石墨烯器件[6]. 其中，时域有限差分(finite-difference time-domain, FDTD)方法[7]结合太赫兹频段的单层石墨烯Drude模型以及辅助差分方程(auxiliary difference equation, ADE)技术常用于模拟石墨烯结构[8]. 虽然FDTD方法数值计算结果的精度较高，但是由于石墨烯薄片一般为原子级厚度，需要大量的空间离散. 传统FDTD方法必须满足CFL(Courant-Friedrich-Levy)稳定性条件，其时间步长主要由计算空间网格长度的最小值决定[9]. 因此，使用该方法仿真石墨烯吸收器计算效率较低，并且内存消耗较为严重.

为了解决传统FDTD方法CFL稳定性条件的问题，几种改进的FDTD方法被提出. 例如交替方向隐式时域有限差分(alternating-direction implicit FDTD,ADI-FDTD)法[10]时间步长不受空间网格长度大小限制，仅受到数值误差的限制，但缺点也是很明显的，必须求解大型矩阵的逆，计算量大且效率较低. 综合FDTD和ADI-FDTD优点的混合显隐式时域有限差分(hybrid implicit-explicit FDTD, HIE-FDTD) 方法[11-13]虽然不如ADI-FDTD方法在理论上具有无条件稳定性，但是其CFL条件仅由两个方向空间离散化决定，并非由最小的空间离散化决定[14]. 因此，HIE-FDTD方法非常适用于仿真石墨烯等在单一方向上具有精细结构的二维材料[15-16].

为了解决阶梯网格划分问题，可以使用非常细的网格离散石墨烯薄片以充分近似曲面边界，但是增加了网格数从而增加了计算时间. 为了在不使用细网格的情况下处理曲面边界，最常用共形技术对其进行处理[17]. 本文通过将共形技术与HIE-FDTD方法相结合，以实现对具有曲面边界的石墨烯结构进行精确仿真.

1 适用于石墨烯的HIE-FDTD方法

数值建模中，石墨烯通常被视为一个薄导电表面，其表面电导率包括两部分：带间电导率和带内电导率，通常用Kubo公式计算得到[18-20]：

式中： σintra和 σinter分别为由对应的载流子跃迁而产生的带内和带间分量[21-22]； ω为角频率；τ为弛豫时间τ=1/(2Γ)，Γ 为散射率；e为 电子电荷；kB为玻尔兹曼常数；T为开尔文温度；h¯为 普朗克常量；；µc为化学势. 在太赫兹波段，由于入射光子能量较小，可以忽略带间跃迁所引起的效应，因此带内跃迁在相互作用中占主导地位. 所以本文只考虑石墨烯的带内电导率，即 σ (ω)=σintra(ω).

设石墨烯的厚度为d，则其相对介电常数可表示为

为模拟石墨烯电导率的色散特性，采用ADE对其进行处理[23-24]，在频域安培方程中引入传导电流密度项，即

式中，

从电导率 σ中分离频率项，式(6)可以表示为

式中，

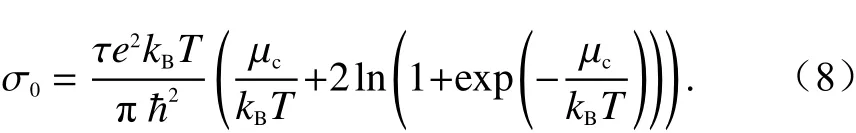
等式(4)表示石墨烯的色散特性，由于HIE-FDTD方法是一种改进的FDTD方法，通过ADE将式(4)变换为时域差分形式得到式(9)，因此通过式(9)可以方便地将其引入到HIE-FDTD方法之中.

1.1 色散HIE-FDTD公式推导

纳入电流密度J的麦克斯韦方程如式(10)和(11)所示：

对式(10)和(11)采用HIE差分格式并结合式(9)可以推导出适用于石墨烯的色散HIE-FDTD迭代公式如下：

使用式(9)替换，同时将式(16)带入到式(12)经过计算得到公式，其迭代公式如下：

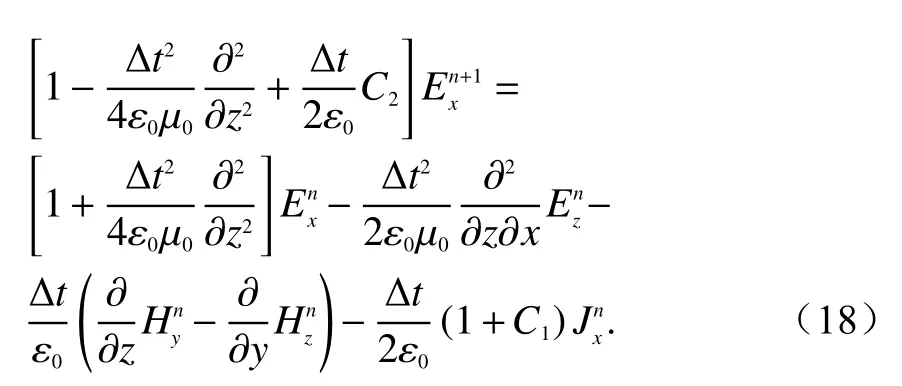
式(18)、(19)、(14)～(17)是最终的色散HIEFDTD迭代公式. 值得注意的是，如果计算区域不包含石墨烯，则式(9)中的系数C1和C2为0.

1.2 色散HIE-FDTD方法稳定性分析

在本节中，讨论色散HIE-FDTD方法的时间稳定性条件. 结合式(9)和式(12)～(17)，我们可得到式(20)：

式中：a=ε0/Δt;b=µ0/Δt;Dp=∂/∂p(p=x,y,z).

不失一般性，三维平面波定义如下：

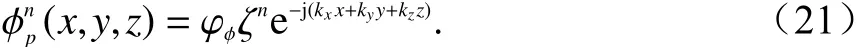
式 中：φ 表 示E，H或J； φφ表示各个场分量的 幅度；ζ表示增长因子；kx，ky，kz分 别表示沿x，y，z方向的波束. 将式(21)带入到式(20)中，并利用中心差分代替空间导数，即sin(kpΔp/2)/Δp)，整理得到式(22)：

要使式(22)存在非零解，其系数矩阵的行列式应为零. 通过求解我们得到：

式中：

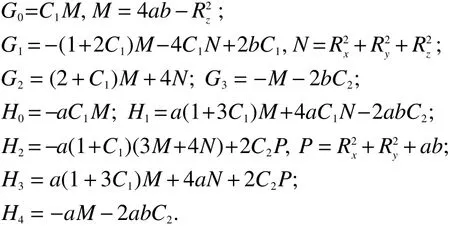
为了保证迭代过程的稳定性，增长因子 ζ的模必须小于1. 通过分析，色散HIE-FDTD的稳定性条件与常规HIE-FDTD的稳定性条件同为[25-26]

1.3 共形HIE-FDTD方法

传统FDTD方法在模拟弯曲物体时常采用阶梯近似法，这样不仅会产生误差，而且会产生伪解. 在过去几十年里为了克服这些困难，人们提出了许多分析弯曲物体的方法，特别是Dey S和Mittra R提出的局部共形FDTD方法，且证明了该方法具有较高的精度和稳定性[27]. 为了可以精确模拟石墨烯的曲面边界，将共形FDTD和色散HIE-FDTD相结合，在x和y方向上使用共形HIE-FDTD方法，在z方向使用传统的HIE-FDTD方法，这样能够保持在仿真石墨烯时具有更高的精确度.

如图1所示，使用共形HIE-FDTD方法仿真石墨烯，只需要在共形网格处对石墨烯取有效电导率并与周围介质进行线性平均，从而修正式(9)中系数C2实现共形HIE-FDTD. 共形网格处石墨烯等效电导率为

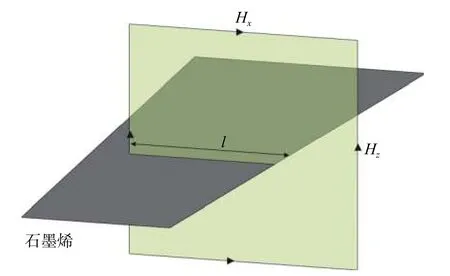
图1 石墨烯曲面边界处的共形网格Fig. 1 Conformal grid at the boundary of the graphene surface

进一步修正共形网格处系数C2，将式(25)带入式(9)系数中得共形网格处修正后C2表达式为

式中，l为石墨烯在共形网格处占据的长度. 该方法在提高精度的同时与原始HIE-FDTD复杂度相同.

2 算例部分

为了验证色散HIE-FDTD方法的有效性，我们对无限大石墨烯进行仿真模拟，并与传统FDTD方法进行对比给出两种方法的优缺点. 然后，利用共形HIE-FDTD方法设计了一种新型的石墨烯圆环结构吸收器，基于这种方法仿真并分析了该吸收器的光学特征.

2.1 色散HIE-FDTD算法有效性验证

为了验证所应用的色散HIE-FDTD方案计算精度和效率，首先采用FDTD方法和色散HIE-FDTD来对无限大石墨烯结构进行对比仿真. 如图2所示，石墨烯位于x，y平面中，它在z方向的厚度为d. 电场是沿着x方向极化的均匀平面波垂直入射在该结构上. 入射波作为一时间函数表达式为

式 中，t0=τ=4×10−12s. 入 射波 频 率 为0～2 THz.

如图2所示，使用Floquet周期边界在x，y方向模拟了无限结构，沿着z方向设置卷积完美匹配层(convolutional perfectly matched layer，CPML)，通过总场/散射场(TS/SF)边界条件将平面波引入到计算域.石墨烯相关参数选择如下：开尔文温度T=300K，化学势 µc=0.1eV， 弛豫时间 τ=1ps ， 散射率 Γ=1/(2τ)，石墨烯厚度d=1.5nm.

图2 包含石墨烯薄片的空间图Fig. 2 A spatial diagram containing graphene flakes

由于单层石墨烯的厚度非常薄，本文中使用两种尺度网格进行仿真：细网格剖分石墨烯，粗网格剖分其他介质. 其中，细网格尺寸选择 Δz=0.3nm. 为了减少由数值色散引起的误差，一般情况下在计算域的其他介质中，最小波长包含的最小网格数(point per wavelength, PPW)应大于8，本文选取PPW为15即Δx=Δy=Δz=10µm. 为了满足CFL稳定性条件，在传统FDTD方案中的时间步长需要满足

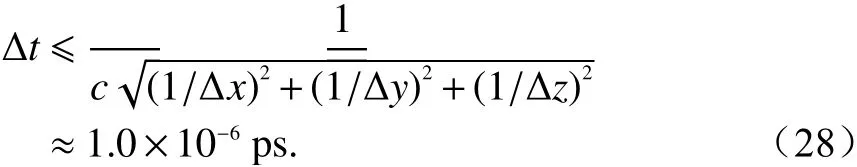
相比之下，在HIE-FDTD方法中，时间步长仅取决 于 两 个 方向的单元尺寸 (例如 Δx和 Δy).

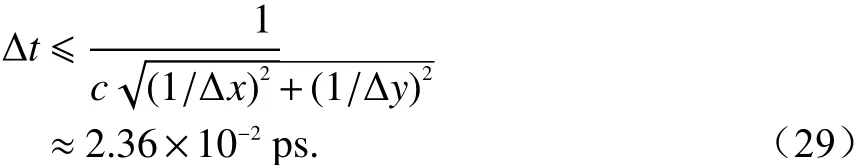
由图3可以看出色散HIE-FDTD方法与传统FDTD方法仿真无限大石墨烯的结果非常吻合. 但是由于传统FDTD时间步长短，制约了计算效率. 而色散HIE-FDTD方法体现出了其对二维材料仿真的高效性. 本文中所有的算例仿真都是在Intel(R)Core(TM)i5-8250U的CPU以及16 G内存的工作平台上进行. 两种计算方法CPU耗时比较如表1所示.

图3 色散HIE-FDTD与FDTD方法电场对比结果图Fig. 3 Comparison result of electric field between HIE-FDTD and FDTD method

表1 FDTD与色散HIE-FDTD方法仿真石墨烯的CPU耗时对比Tab. 1 Comparison of CPU time consumption between FDTD and dispersive HIE-FDTD methods for simulating graphene

从表1可以看出，FDTD方法和色散HIE-FDTD方法CPU总耗时分别为750 min和31 s. 虽然色散HIE-FDTD方法采用的时间步长非常大，但色散HIEFDTD方法总耗时仅为FDTD方法总耗时的1/1451.

2.2 新型石墨烯吸收器设计

本文设计的一种新型石墨烯吸收器结构如图4所示，其由三层介质组成，包括顶层环状石墨烯、中间介质层以及底部完美电导体(perfect electrical conductivity, PEC). 该吸收器为周期结构，结构单元在x和y方向周期排布，周期P=4 µ m. 顶层石墨烯薄膜的结构为圆环，圆环内直径d1为 2.2 µ m，外直径d2为 2.48 µ m. 介质层是介电常数为2.35的环烯烃共聚物. 由于色散HIE-FDTD方法对石墨烯的仿真非常有效，我们用它结合共形技术来分析本文提出的新型石墨烯吸收器的光学特性.

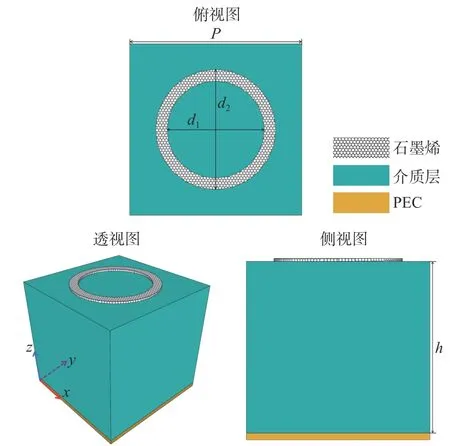
图4 石墨烯吸收器结构图Fig. 4 Structure of graphene narrow-band absorber

吸收器的吸收率表达式为A=1−T−R，其中T表示传输系数，R表示反射系数. 由于底部采用PEC，所以在太赫兹入射的传输系数为0，因此吸收率的表达式可以简化为A=1−R.

太赫兹电磁波垂直入射至吸收器表面，在石墨烯化学势为0.7 eV、中间介质层厚度为18 µ m、圆环宽度为0.14 µ m的前提下，得到该吸收器的吸收率曲线如图5所示. 可以看出，在2.68 THz处吸收率趋近于1. 说明该吸收器在2.68 THz附近具有良好的吸收特性.

图5 采用共形HIE-FDTD方法计算的吸收率Fig. 5 Use conformal HIE-FDTD method to calculate absorption rate

众所周知，在太赫兹频率范围内，石墨烯的费米能级可以通过化学掺杂或静电掺杂发生改变，从而实现调节石墨烯表面电导率的功能. 利用这一特性，该吸收器可以实现可调谐性. 吸收器的吸收率曲线随化学势的变化如图6所示. 可以看出，随着化学势从0.5 eV增加到1 eV，吸收器的吸收频率从2.25 THz移动至3.25 THz. 同时可以看出，吸收率随着化学势的增加而增加，这是因为费米能级的增加会导致等离激元共振的等离子体浓度逐渐增加，当化学势µc=0.7 eV时到达最佳状态. 数值实验结果表明所设计的石墨烯吸收器工作频率可以通过控制其化学势进行调节.

图6 化学势对吸收率的影响Fig. 6 The effect of chemical potential on absorption rate

为了进一步分析吸收器的几何参数对吸收性能的影响，石墨烯的化学势选择为0.7 eV，保持其他参数不变. 通过计算得到了圆环宽度对吸收率曲线影响的变化情况如图7所示. 当圆环宽度由0.10 µ m增加到0.20 µm时，吸收峰频率由2.42 THz移动到2.97 THz，即随着圆环宽度的增加吸收峰出现了蓝移，吸收率先增加再减小. 在圆环宽度为0.14 µ m时达到最佳状态，吸收率趋近于1. 说明该吸收器可以通过调节几何参数对工作频率进行选择.

图7 圆环宽度对吸收率的影响Fig. 7 Effect of ring width on absorptivity

3 结 论

本文应用HIE-FDTD方法完成了对石墨烯吸收器的数值模拟. 该方法的时间步长不受石墨烯厚度离散的限制，因此非常适用于分析在某一方向具有精细结构的二维材料. 同时，本文为了能够精确模拟具有弯曲边界的石墨烯将共形技术与本文中色散HIE-FDTD方法相结合，并使用共形HIE-FDTD方法设计了一种工作在太赫兹频段的可调谐完美超材料吸收器. 数值结果表明，本文设计的吸收器工作频率可以通过调节石墨烯的化学势和几何参数进行改变，这一结果表明基于石墨烯的太赫兹吸收器具有可调谐性. 本文所设计的吸收器结构为一种单频带可调谐完美吸收器，为了实现对入射波的多带或者宽带吸收，可以通过在该单元结构中放置多个尺寸相似的石墨烯圆环并采用上述方法进行分析.