基于相互无偏基和拟合优度检验的频谱感知方法

吴皓 张涛 陈跃 王海泉 潘鹏

（1. 中国电子科技集团公司第七研究所，广州 510310；2. 中国人民解放军91977部队，北京 100036；3. 杭州电子科技大学，杭州 310018）

引 言

随着无线通信技术的发展，大量的无线通信需求需要大量的无线频谱，频谱资源紧张的问题日益严重. 而另一方面，国际通用的静态频谱分配机制，即为特定的通信业务划定固定的频率范围，造成无线频谱的平均利用率很低. 这种分配机制尽管使得不同业务间的干扰得到有效避免，但也造成频段资源空闲时间的增加，这就使得有限的频谱资源非但得不到良好的利用反而遭到了浪费. 为使以上问题能够得到有效解决，近年来，认知无线电(cognitive radio, CR)技术作为一种频谱共享技术，得到了快速发展. 各种频谱感知技术已被提出[1-9]，比较经典的主要有以下方法. 文献[4]介绍了基于信号能量的能量检测法，其可以在不知道用户信号任何信息的条件下完成对目标频段的频谱感知. 因此，能量检测法在CR领域中的应用很广. 但它也存在着一些不足之处，如当系统的信噪比较低时，算法的效果并不是很好，并且算法无法分辨已调信号和干扰信号，而干扰信号会使能量检测器做出错误判决. 文献[5]研究了在噪声不确定的情形下，能量检测所需的样本数量和检测概率的关系，分析了噪声不确定性对能量检测的影响. 文献[6]介绍了匹配滤波器感知法，该方法是基于最大化信噪比准则的方法，其准确性高且检测速度快. 但该方法在检测时必须依赖主用户信号的先验信息，这限制了它在实际中的应用. 此外，当主用户信号类型不同时，该方法需设计出与信号类型相应的匹配滤波器，这增加了设备的成本和复杂度. 文献[7]介绍了循环平稳特征检测法，信号在送入无线信道之前，一般都要经过调制、调频、添加循环前缀等处理，因此信号的某些特性会体现出一定的周期性，这些特性被称为循环平稳特性. 基于这些特性，循环平稳特征检测法用来区分用户信号和噪声. 该方法在环境较差的场景下可以保持较好的检测性能，而且它还能够分辨不同的主用户信号类型，但是该方法需对接收信号进行长时间的观测，在进行判决时也需用到主用户信号的先验信息，计算复杂度较大.

以上方法都是基于信号的某种特征或信号的某个参数进行检验的方法. 文献[8]在2009年首次将频谱检测表述为非参数的拟合优度检验，而后，此方法得到了广泛的研究[9-13]. 文献[9]将神经网络应用于拟合优度检验当中，通过降低用户信号的相关性从而提高系统检测概率. 文献[10]将接收信号样本协方差矩阵的最大特征值与迹的均值的比值作为拟合优度检验的对象，从而有效地避免了噪声不确定性的影响. 本文的研究内容主要集中在基于拟合优度检验的频谱感知方法. 拟合优度检验算法通过统计分布函数挖掘数据信息，从而做出判决. 拟合优度检验的基本思路是：当仅有噪声时，样本服从于噪声分布，当用户信号存在时，则样本不会服从噪声分布，因此便可将信号存在的问题转换成其样本是否满足服从噪声分布这一条件. 由此可知，拟合优度检验是考虑信号整体特征，而非信号的某个参数特征，并且，它不需要任何信号的先验信息.

对于一个统计实验，一般来说，样本数越多，拟合优度检验的检测结果更加准确. 基于这一思想，为了提高拟合优度检验的准确性，在本文中我们首先利用相互无偏基(mutually unbiased bases, MUB)矩阵对接收信号样本做信号变换使得样本数增加，然后采用KS(Kolmogorov-Smirnov)检验方法进行拟合优度检验. MUB由一组正交矩阵或正交基组成，且相互之间的相关性很弱，因而经这些正交矩阵变换后的数据也保持了弱相关性. 这一性质能够使得由变换而增加的数据具有相对的独立性，从而提高频谱检测的效果. 事实上，本文的分析和仿真结果均表明，利用MUB矩阵对接收样本做数据处理再进行KS检验的效果要优于常规的KS检验.

1 基于拟合优度检验的频谱感知技术

1.1 二元假设检验模型

频谱感知的问题一般用二元假设模型表示，假设H1和H0分别代表主用户存在和主用户不存在，即H1表 示频段被占用，不能被次用户使用；H0表示频段空闲，可以被次用户使用. 频谱感知有如下表现形式：

式中：r(t)表 示接收信号；s(t)表 示发送信号；n(t)表示高斯白噪声. 基于此检验模型，即可选择检测算法对r(t)进 行处理得到判决统计量T，最后对比判决统计量和门限值 γ的大小从而判断频谱的占用情况[5-6]：

对于检测结果，频谱感知的指标一般有检测概率Pd、 虚警概率Pfa和漏检概率Pm. 用D0表示认知用户认为主用户不存在的情况，用D1表示认知用户认为主用户存在的情况.

检测概率Pd表示主用户占用某频段时，被次用户检测出该频段被占用的概率，表达式为

检测概率越高，认知用户就可以更好地感知频谱空穴，从而提高频谱的利用率.

虚警概率Pfa表示频段未被占用时，次用户误判该频段被占用的概率，表达式为

若虚警概率过高，会使认知用户无法正确识别频谱空穴，使得频谱利用率无法增加.

漏检概率Pm表示当某频段被占用时，认知用户判定主用户不存在的概率，表达式为

若漏检概率过高，会使认知用户把已使用的频谱当作频谱空穴，从而干扰主用户的通信.

1.2 基于拟合优度检验的频谱感知

文献[8]首次从拟合优度检验的角度去考虑频谱感知问题：当没有信号传输时，样本服从噪声分布，而信号的出现会改变样本的分布，因此可通过判断样本的分布情况来判断信号是否存在.

记观测样本为X，当没有传输信号时，样本服从于噪声的分布，分布函数记为F∗(x). 当信号出现时，样本便不会服从于分布F∗(x). 因此，检测信号出现就等价于检验观测样本X是否服从零假设给出的噪声分布F∗(x)，若样本服从噪声的分布则判定信号不存在，否则就判定信号存在，有

拟合优度检验可以不是针对直接的观测信号，主要针对的是实数样本集，由于通信系统中的信号一般都是复数的形式，所以在进行拟合优度之前要对初始的样本值进行取模操作. 对于变换样本时首先确定其在零假设下的理论分布. 以基于经验累积分布函数(empirical cumulative distribution function，ECDF)型拟合优度检验为例，信号检测的通用流程如下：

首先确定检验算法，即样本的ECDF和理论分布函数的差值度量函数；再根据确定的检验算法和虚警概率Pfa以及样本长度n， 确定门限γ；接着根据观测样本(或变换样本)的形式确定零假设H0下样本理论分布F∗(x)；然后根据选用的检验算法计算检验统计量；最后检验判决.

在介绍具体的检验方法之前，我们先给出ECDF的定义，若Fn(x)是 样本X的 经验概率分布，X={x1,x2,···,xn}，则

式中，1 (·)为 示性函数，若xi≤x， 则1 (xi≤x)为1，否则为0. 在计算经验概率分布时，可以先对样本值按照升序进行排序，这样就可以通过简单的计算得到所有样本的ECDF值，计算公式如下：

判决统计量的值取决于样本理论分布和经验概率分布的差异程度，判决统计量越大说明其差异程度越大，当判决统计量大于门限时，判断为信号存在，否则就只存在噪声. 不同的拟合优度检验方法对其差异程度的计算也就是判决统计量的计算不同，以KS检验为例，当样本为X时其判决统计量Dn的计算如下：

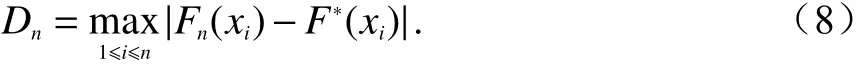
2 MUB矩阵介绍

2.1 MUB矩阵的定义

若B1,B2,···,Bd是M×M阶的d个酉阵，即

记Bj=[bj1,bj2,···,bjM]， 对于任何的i≠j，有

2.2 MUB矩阵的构造

2.2.1 M=p(p为素数)

当M为素数时，可直接构造MUB矩阵，构造方法如下：

式中： ωp=ej2π/p,Fp={0,1,···,p−1}. 当a,b都取定而x遍 历数域 Fp即x依 次取从0到p−1的数时，便得到一个p维 的向量va,b； 当a取 定而b、x遍 历数域 Fp便得到p个向量，将这p个向量称作一组基Ba； 当a,b,x遍历数域 Fp便 得到p个 基，最终生成一个维度为M×M2的矩阵.

2.2.2 M=ps(p 为 奇素数， s>1)

当维度为素数幂时，构造MUB矩阵需要用到有限域的知识. 关于有限域理论的知识由于篇幅原因在此不做赘述，读者可参考文献[14]. 在这一节中假设p>2，为了介绍MUB矩阵的构造，有必要先介绍有限域中迹(trace)的定义，如下所示：

定义 假设α ∈F=Fpm，K =Fp，t raceF/K(α)定义如下：

利用trace的概念，则可以构造出MUB矩阵. 具体的构造方法如下：

设M=q=ps， 其中p为 大于2的素数，s为正整数. 令

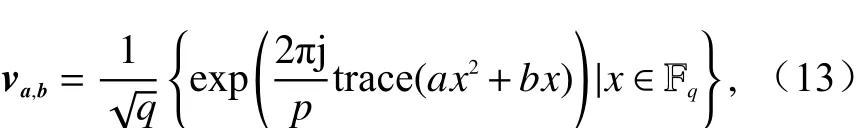
则当x取 遍 Fp中的所有元素时，va,b形 成一个q维的向量. 令

则Ba形 成一个酉阵，维度为q×q， 而 {Ba1,Ba2,···,Baq}形成一个维度为M×M2的MUB.

2.2.3 M=2n(n >1)[15]

当M为2的幂时，设q=M. MUB矩阵的构造如下：

当x取 遍 Fq中 的所有元素时，va,b形 成一个q维的向量.令

则Ba形 成一个酉阵，维度为q×q， 而 {Ba1,Ba2,···,Baq}形成一个维度为M×M2的MUB.

3 基于MUB的KS检验

MUB中的每个酉矩阵都表示了空间中的一个座标架，并且不同座标架之间的相关系数都很小，仅为(M为空间的维度，即样本的长度)，这样样本经过MUB矩阵变换后，就可以产生几乎独立的新的样本. 基于这些新样本，可以做出更加准确的判决.基于MUB的拟合优度检验过程如图1所示，具体的数学推导过程如下所示，应用场景为加性高斯白噪声信道.

图1 基于MUB的拟合优度检验过程Fig. 1 Process of goodness fit test based on MUB

设{y1,y2,···,yM}为样本集，当样本未经MUB矩阵转换，KS检验的判决统计量

设矩阵Bi(i=1,2,···,M)为MUB中的任一矩阵，令

这样就得到M2个数据

基于这M2个数据，进行拟合优度检验. 具体的检测方案如下：

该方法是将样本数扩大到M2，所以首先对新的样本集Z进行升序处理. 当 {y1,y2,···,yM}是均值为零、方差为 δ2的复高斯噪声，并且其实部和虚部都是独立同分布时，由于处理之后的样本集的分布并没有大的改变，因此对每个样本值取模以后，其模值的概率分布函数仍为瑞利分布. 其分布函数和经验函数如下所示：

其判决统计量

4 仿真实验

仿真基于高斯信道模型，假设噪声已知且是高斯信道，发送信号为16QAM调制信号. 检测模型如下所示：

式中：xi表示接收样本的第i个分量； ωi表示噪声的第i个分量；ρ表示信噪比；h表示信道；si表示发送信号的第i个分量；M表示发送端的天线数，即信号的长度.

由于检验的门限值会随着样本数和虚警概率的改变而改变，因此我们在仿真前必须确定好相应的门限值. 本次仿真的虚警概率统一定为5%，通过10 000次蒙特卡洛确定检验门限值，如表1所示.

表1 两种检验方式的门限值Tab. 1 Threshold values of two inspection methods

基于高斯信道环境，采用基于MUB的KS检验算法针对发送天线数M分别为16、32和64时进行仿真，并同传统的KS算法做比较，具体的仿真结果见图2.

图2 KS检验仿真对比结果Fig. 2 KS test simulation comparison results

从图2仿真结果可知，采用基于MUB的KS检验对信号进行判决，其检测概率有一定程度的提高，提高的幅度分别为2 dB、1.5 dB、1 dB以上.

5 结 论

本文介绍了将拟合优度检验作为频谱感知的方法以及MUB矩阵的构造方法，相比于传统的拟合优度检验方法，本文在此基础上通过MUB矩阵对信号样本进行预处理从而提高了信号的检测概率，并且该方法的计算复杂度主要体现在数字的乘法，在现有的技术条件下很容易实现. 除了KS检验之外，还有多种拟合优度检验的方法，皆可尝试用MUB矩阵对样本做预处理以达到提高信号检测概率的目的，这也是我们后续的研究方向.