反射面天线焦面场采样研究与相控阵馈源设计

田佳怿 杜彪 伍洋 刘胜文

（中国电子科技集团公司第五十四研究所, 石家庄 050081）

引 言

随着雷达、卫星通信、射电天文等技术的飞速发展，对高增益、大视场天线的需求日益增加. 多波束天线技术可以有效地扩大天线的视场，常见的多波束天线有相控阵天线[1]、反射面天线[2]和介质透镜天线[3]三种. 其中配备相控阵馈源(phased array feed,PAF)的反射面天线结合了反射面天线的高增益、低成本和相控阵天线波束扫描灵活等优点，可以形成多个连续覆盖、性能优良的波束，有效地扩大反射面天线的视场[4-5].

基于PAF馈电的反射面天线正成为研究热点.文献[6]结合制冷技术设计出L波段高灵敏度双极化偶极子PAF，并用于绿岸的射电天文望远镜. 文献[7]设计了一种基于紧馈蝶形偶极子天线的宽带PAF，基于经验其单元间距为0.5个波长. 文献[8]和[9]分别为中国五百米口径球面射电望远镜(Five-hundred Meter Aperture Spherical Telescope, FAST)设计了工作在L波段的PAF，都是通过固定单元间距改变单元数量，以及固定单元数量改变单元间距，计算比较不同参数下反射面天线性能的方法，来确定PAF的单元数量和单元间距. 文献[10]是在固定单元数量的情况下，计算了超方向性单元的单元间距随射电望远镜巡天速度的变化规律，以巡天速度最高时的单元间距作为最优单元间距，这与文献[8]和[9]中确定最优单元间距的方法相同，但得到的单元间距并不是最优的，仅是小范围内的最优值. 文献[11]和[12]是通过焦面场公式以及Nyquist采样定理确定单元间距，即采样频率大于焦面场空间谱最高频率的2倍，这样确定的单元间距能在一定程度上恢复焦面场，但不是最优单元间距. 文献[13]主要针对小焦径比的反射面天线，研究天线效率最高时PAF的单元间距和单元数量，且只考虑了PAF正方形排布时的情况，研究了PAF的单元数量和单元间距对反射面天线性能的影响，认为合成一个波束的单元数量为7×7到9×9时，天线的口径效率最高，但单元数量过多，造成后端链路成本过高. 文献[14]提出对于宽带焦面阵馈源，低频时单元间距和单元电尺寸较小，可以工作在PAF模式，多个单元组阵合成一个波束；在高频时，单元间距和单元电尺寸较大，可以工作在馈源阵模式，每个单元都可独立形成一个波束.上述研究中，PAF的单元间距一般是采用经验值或通过焦面场公式和Nyquist采样定理确定单元间距，还有通过计算比较PAF取不同参数时反射面天线的性能，来确定PAF的参数. 然而缺少对PAF的阵列排布、单元间距、单元数量、焦径比、扫描角与天线口径效率之间关系进行系统和深入的研究，且未给出PAF参数的选取原则，难以指导PAF的设计.

本文通过分析不同焦径比和不同扫描角时反射面天线焦平面场的特性，初步确定了PAF的采样范围；深入研究了PAF参数对天线口径效率的影响，给出了PAF的最优采样范围、单元间距和阵列规模，用最少的单元数量实现最高的口径效率，提高PAF的性价比；导出了PAF的单元间距和单元数量的计算公式，给出了PAF参数的选取原则，并通过一个设计实例验证了本文研究和分析方法的正确性，为PAF的设计提供了理论依据.

1 焦面场分析

焦面场分析是进行馈源设计的重要方法[12,15]. 通过计算从空间接收的电磁波在天线焦平面形成的场分布，可以得到馈源的位置及其口径需要实现的场分布，让馈源的口径场与焦面场共轭匹配，从而实现较高的天线增益.

图1给出了前馈抛物面天线的焦面场分布图，D=400λ，f/D=0.6. 当均匀平面波轴向入射，经抛物面反射后，在焦平面上会激励起一组明暗交替的能量环分布. 焦点附近的电场最强，馈源的相位中心一般在这个位置.

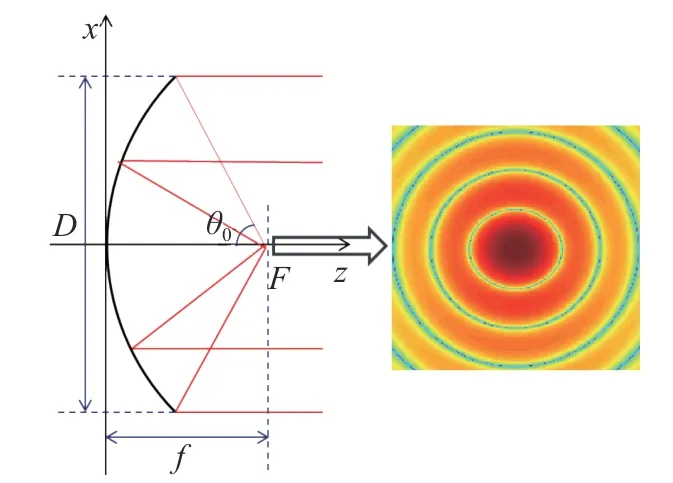
图1 抛物面天线的焦面场示意图Fig. 1 Focal field of parabolic antenna

当均匀平面波沿抛物面天线轴向入射时，焦面场的主极化分量可表示为[16]

式中：E0为入射场强；D和f分别为天线的口面直径和焦距；λ为工作波长；J1为一阶第一类贝塞尔函数；u0=krfsinθ0，rf为 焦平面上的点到焦点的距离；θ0=2arctan(D/(4f))为反射面边缘对馈源的半张角，只与焦径比有关.

令Eco=0，可得焦面场中零深的位置到焦点的距离为

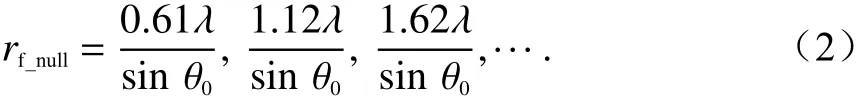
图2给出了焦面场各个零深的位置随焦径比f/D的变化情况. 可以看出，f/D越大，θ0越小，零深位置到焦点的距离越远. 如果要采样焦面场第一零深以内的区域，f /D越大，PAF的采样范围就越大.

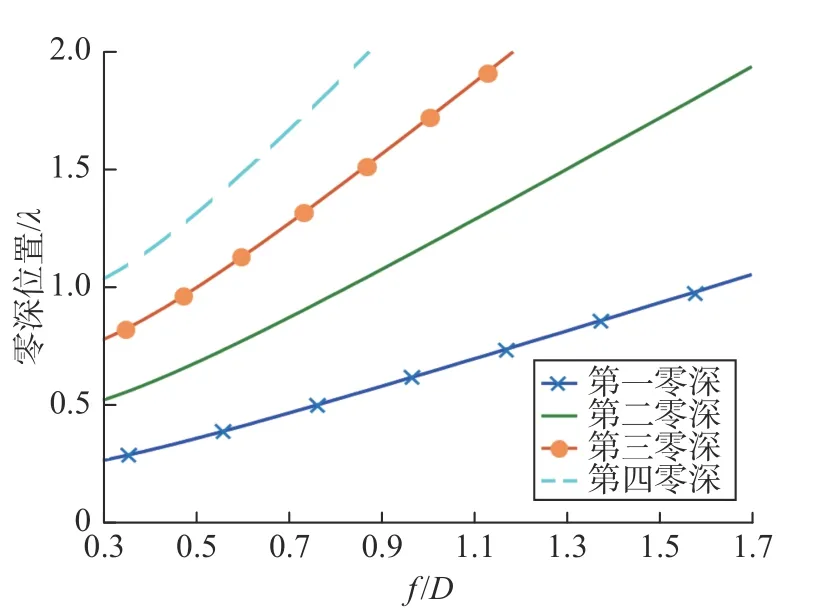
图2 零深位置到焦点的距离随焦径比的变化Fig. 2 The distance from null position to the focus with f/D

图3给出了抛物面天线焦面场各环区域的能量占比随焦径比的变化情况，此时焦径比的范围为0.3～1.7. 可以看出，第一零深以内区域聚集了大部分能量，且焦径比越大，能量占比越高，特别是f/D≥0.7时，第一零深以内能量占80%以上. 因此，对于大焦径比的天线，在其第一零深以内的区域进行采样就可以接收到足够多的能量，而对于小焦径比的天线，则需要在更大范围(第二零深或第三零深)内采样，才能获取大焦径比天线接收相同的能量.

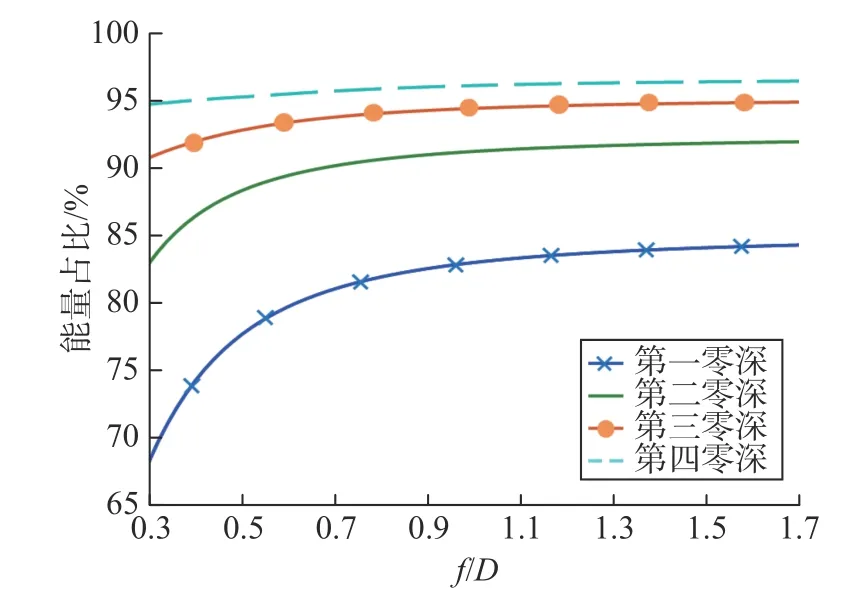
图3 焦面场各区域能量占比随焦径比的变化Fig. 3 Energy in each region of the focal field with f/D

经计算可知，卡塞格伦天线、格里高利天线等双反射面天线的焦面场分布与相同等效焦径比的前馈抛物面天线基本一致，故双反射面天线可等效为前馈抛物面天线来分析. 此外，焦径比相同的情况下，不同口径大小的反射面天线的焦面场分布相同，因此，本文的后续研究都采用直径为400λ的前馈抛物面天线来进行分析计算.

2 焦面场采样研究

通过仿真分析，研究PAF的阵列尺寸和单元间距对天线口径效率的影响，进而得到PAF参数和反射面天线性能之间的关系，总结最优的采样范围和单元间距，并推导出最优单元数量的计算公式.

2.1 研究方法

首先利用GRASP软件，建立抛物面天线的仿真模型，计算天线的焦面场分布；然后根据焦面场分布，初选PAF阵列的参数，包括单元尺寸、单元间距、排布方式和单元数量，利用共轭场匹配(conjugate field matching, CFM)法算出阵列各单元的激励系数；将单元方向图、激励系数和单元坐标输入GRASP软件中，建立PAF的模型，计算得到PAF的辐射方向图；最后，用该方向图照射反射面天线，得到天线的口径效率，来研究PAF参数与口径效率的关系.

在上述研究方法中，单元型式选取和单元方向图的计算是研究的重要环节之一. 当确定单元型式后，单元方向图一般通过解析公式或商用电磁仿真软件计算得到. 简单常用的单元天线方向图的计算公式可参考关于天线理论的教材[17]，例如半波振子、矩形波导等；而Vivaldi天线等其他单元，结构较复杂，其方向图则需要利用商用软件计算. 为了分析方便和总结规律，本文的PAF单元采用口面场均匀分布的理想波导，其口面位于焦平面上，不考虑单元之间的互耦对辐射性能的影响，其辐射场可以通过口面场积分公式计算[17]. 阵列排布方式可选正方形排布和六边形排布，单元尺寸等于单元间距.

CFM法是通过计算单元所在位置焦面场的共轭值，确定该单元的激励系数，使馈源口面场与天线焦面场匹配，从而获得最高的天线效率. 此外，波束合成算法、最大方向性算法和最优灵敏度算法[18]通过馈源照射反射面天线，计算天线的辐射方向图，得到天线的方向性系数或灵敏度关于波束合成因子的关系式，再求导得到最大值. 在不考虑互耦的情况下，本文采用CFM法得到的焦面场采样的一般规律与其他两种方法一致. 在实际工程设计中，如果追求最大方向性或最大灵敏度，可基于本文的初始参数来计算波束合成因子，得到PAF每个单元的幅度和相位加权值.

下面利用上述分析方法研究不同焦径比、不同扫描角时PAF参数对天线口径效率的影响，总结最优采样范围、采样间隔(单元间距)和单元数量，给PAF的初始设计参数的选取提供理论依据.

2.2 焦面场采样

由图3可知，焦面场第一零深以内区域聚集了68%～84%的能量，首先研究在第一零深以内区域进行采样时，反射面天线能够实现的最高口径效率以及对应的单元间距.

图4给出了PAF采样焦面场第一零深以内区域的情况下，反射面天线口径效率随单元间距的变化规律，f/D分别为0.5、1、1.5，PAF六边形排布，当单元间距增大时单元数量随之减少. 可以看出：随着焦径比增大，最大口径效率在升高. 在同一焦径比的情况下，天线能实现的最大口径效率是一定的，如f/D=1时，最大口径效率为81.6%，即使单元间距变小，即采样点变密，口径效率也不会明显增加；当f/D为0.5～1时，最优单元间距为0.33λ/sin θ0(0.41λ～0.7λ)，即采样第一零深以内区域时，当天线口径效率达到最大值时需要的单元数量最少时的单元间距；当f/D为1.5时，最优单元间距为0.23λ/sin θ0(0.71λ).由此可以得出：最优单元间距与焦径比有关，焦径比越大，最优单元间距也越大；当焦径比固定时，随着单元间距连续增大到某些值时，部分单元超出了第一零深以内区域，于是采样区域内的单元数量会突然减少，此时仅能采样第一零深以内的小部分区域.因此口径效率会出现陡降的现象，随着单元间距的进一步增大，单元数量不变的PAF采样第一零深的范围也在增大，此时口径效率会逐渐增加到最大值.

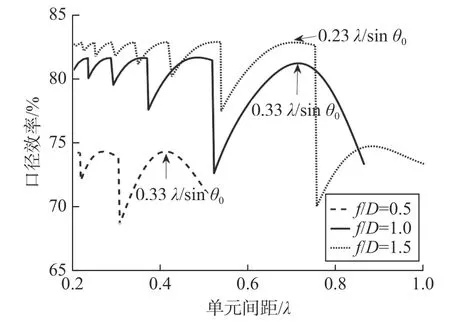
图4 采样第一零深以内区域时口径效率随单元间距的变化Fig. 4 Aperture efficiency with element spacing when sampling in the area within the first null

PAF分别采用六边形排布和正方形排布以最优单元间距采样第一零深以内区域的情况下，天线的口径效率是相同的. 图5给出了采样第一零深以内区域时反射面天线的口径效率随焦径比的变化情况.可以看出，焦径比越大，天线的口径效率越高，口径效率的计算结果与图3中焦面场能量占比情况是一致的.

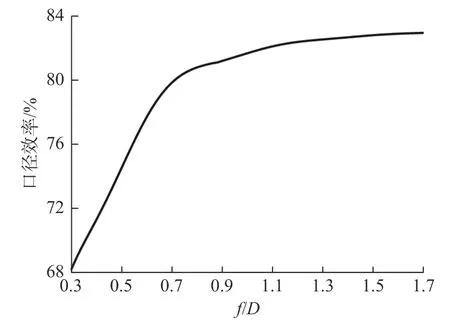
图5 采样第一零深以内区域时口径效率随焦径比的变化Fig. 5 Aperture efficiency with f/D when sampling in the area within the first null

图6给出了焦径比在0.3～1.7，PAF采样第一零深以内区域的情况下六边形排布和正方形排布的PAF最优单元间距随焦径比的变化情况. 可以看出，最优单元间距与PAF的阵列排布方式有关，工程设计时应选取最优单元间距更大的排布方式，此时的单元数量更少，馈源的性价比更高. 例如，f/D=0.3～0.7时，PAF应采用正方形排布，其最优单元间距更大，仅需要4个单元，而六边形排布的PAF则需要7个单元，但它们照射天线时的天线口径效率是相同的；f/D=0.7～1.0时，PAF应采用六边形排布，需要7个单元，而正方形排布的PAF则需要9个单元；f/D=1.0～1.5时，PAF应采用正方形排布，需要16个单元，而正方形排布的PAF则需要19个单元. 此外，虽然焦径比越大，天线的口径效率越高，但需要的采样范围越大，单元数量就更多. 因此，实际应用中选取焦径比时，需要考虑上述因素，并非焦径比越大越好，应合理选择焦径比以最少单元实现最高的口径效率.

图6 采样第一零深以内区域时最优单元间距随焦径比的变化Fig. 6 Optimal element spacing with f/D when sampling in the area within the first null

图7给出了PAF的单元数量为19，采用最优单元间距时不同焦径比反射面天线的口径效率. 可以看出，f/D=0.75时，口径效率最高，此时PAF采样焦面场位于第二零深以内区域. 这是因为当焦径比大于1.1时，采样焦面场第一零深以内区域需要的单元数量更多(19个单元)，而用同样数量的单元也可以采样小焦径比天线更大范围的焦面场(如第二零深以内区域)，这时小焦径比天线就能实现比大焦径比天线更高的口径效率. 因此，进一步证明，在设计PAF时应综合考虑焦径比的选取.

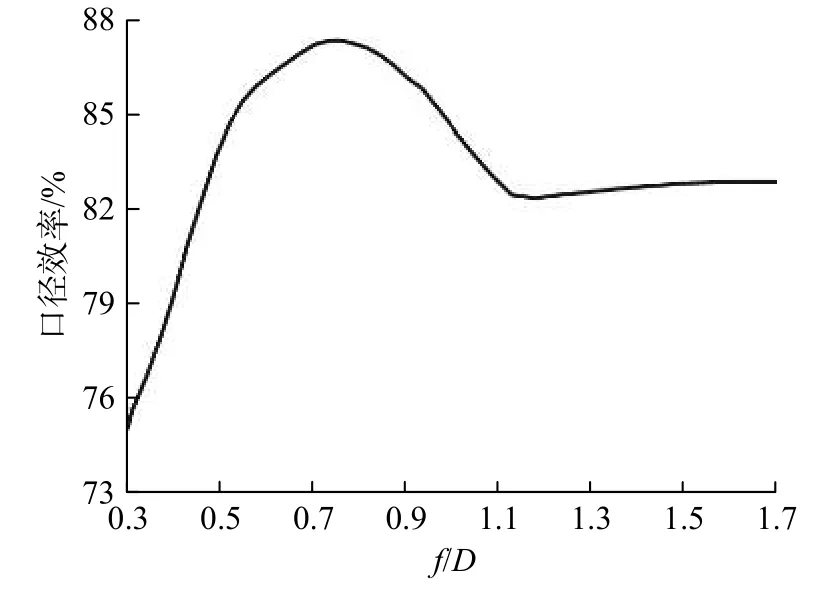
图7 混合采样第一和第二零深以内区域时口径效率随焦径比的变化Fig. 7 Aperture efficiency with f/D when mixed sampling in the area within the first null and second null

上述研究仅针对轴向波束，而PAF是用作多波束天线的馈源，因此，还需重点研究扫描波束的情况.图8给出了扫描波束的焦面场，f/D分别为0.35、0.5和0.7，平面波沿与反射面天线轴线夹角0、2、4、6、8、10个波束宽度斜入射. 可以看出，焦径比越大，各零深的圆半径越大，相同扫描角度的波束对应焦面场到焦点的距离越远，且其散焦的程度越轻.

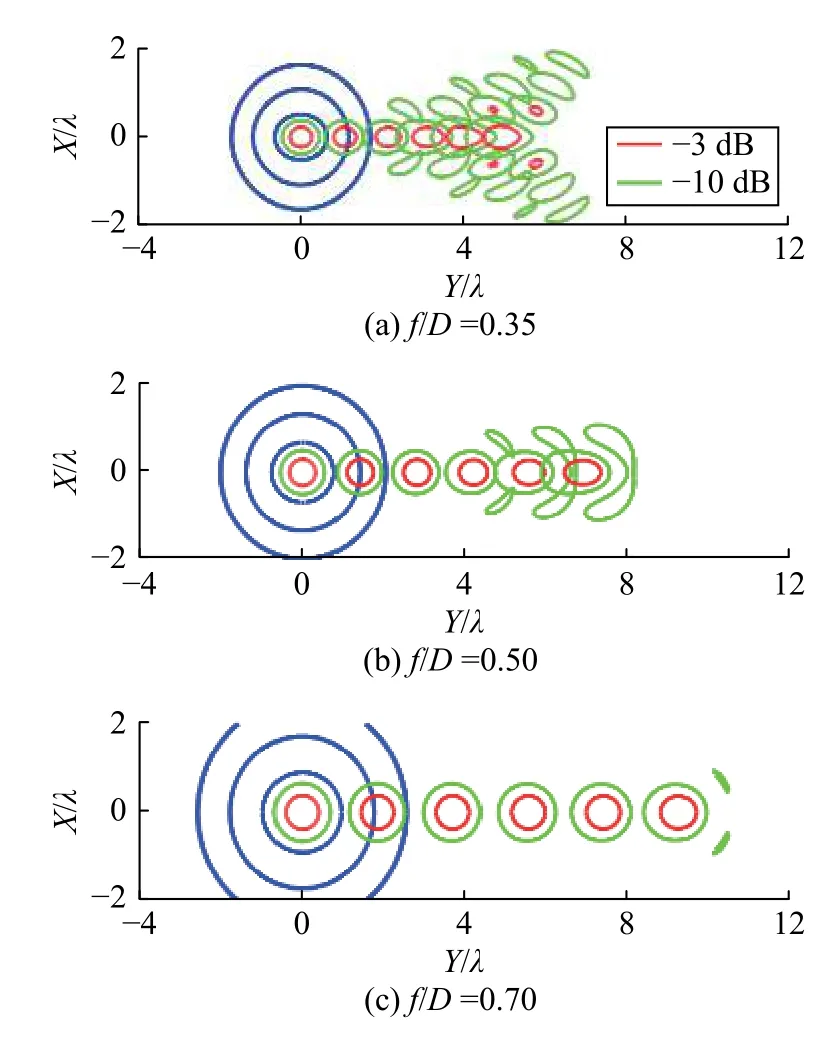
图8 扫描波束的焦面场分布Fig. 8 Focal field of scanning beams

在f/D较小的情况下(f/D<0.7)，波束的口径效率较低，偏轴波束对应的焦面场散焦更严重，仅采样第一零深以内区域不能满足天线效率要求，需要扩大采样范围. 图9和图10分别给出了反射面天线口径效率和最优单元间距与焦径比的关系曲线，此时PAF采样范围为第二和第三零深以内. 可以看出，焦径比越大，口径效率越高，这与图6中第一零深以内采样时口径效率与焦径比的变化规律一样. 从图10看出，最优单元间距与采样范围有关，采样范围越大，最优单元间距越大，且六边形排布比正方形排布的单元间距要大，此时选六边形排布方式为最优.

图9 采样第二或第三零深以内区域时口径效率随焦径比的变化Fig. 9 Aperture efficiency with f/D when sampling in the area within the second null or third null

图10 采样第二或第三零深以内区域时最优单元间距随焦径比的变化Fig. 10 Optimal element spacing with f/D when sampling in the area within the second null or third null

图11给出了PAF分别采样第一、二、三零深以内区域的情况下，要使口径效率分别大于60%和70%，反射面天线能够实现的最大扫描角度随焦径比的变化情况，其中最大扫描角度为半功率波束宽度(half power beam width, HPBW)的 倍 数(按 70λ/D估算). 可以看出：同样的采样范围，焦径比越大，最大扫描角度越大；同一焦径比，采样范围越大，最大扫描角度越大；同一焦径比和同样的采样范围，要求的效率越高，最大扫描角度就越小.

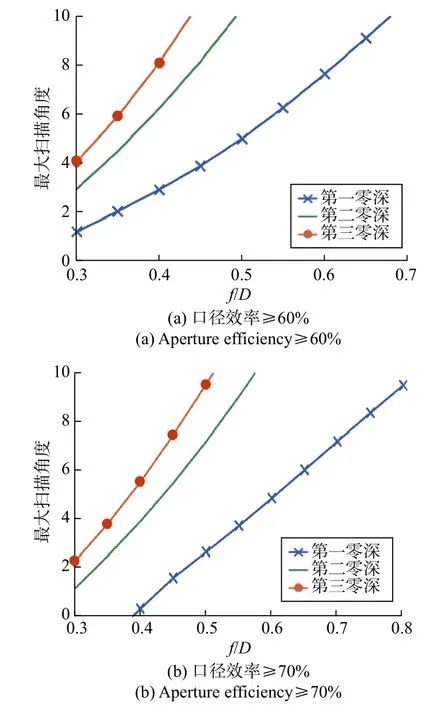
图11 不同口径效率下最大扫描角度随焦径比的变化Fig. 11 Maximum scanning angle with f/D at different aperture efficiency

当单元尺寸小于单元间距时，通过计算可知，天线的口径效率与单元尺寸等于间距时得到的结果基本一致，因此本文的研究成果也可指导由单元尺寸小于间距的单元组成PAF的设计.

2.3 单元数量计算

通过馈源的偏焦，反射面天线可实现波束扫描，通过PAF照射反射面天线可同时形成多个相互交叠的波束，实现连续的大视场覆盖. 研究反射面天线的焦面场范围，可确定PAF的尺寸. 图12给出了反射面天线波束偏转示意图.

图12 反射面天线波束偏转示意图Fig. 12 Diagram of Beam deflection of reflector antenna

焦面场大小可根据波束偏转因子(beam deviation factor, BDF)进行估算[19]：

式中：θb和 θf分别为波束偏转角和馈源偏置角；d为馈源横向偏离焦点的距离；k为与f和d相关的系数，取值0.3～0.7.

偏转角最大为θbmax的波束，对应的馈源相位中心到焦点的距离为

一般来说d≪f，即θf很小，(tanθf)′=sec2θf≈1，所以

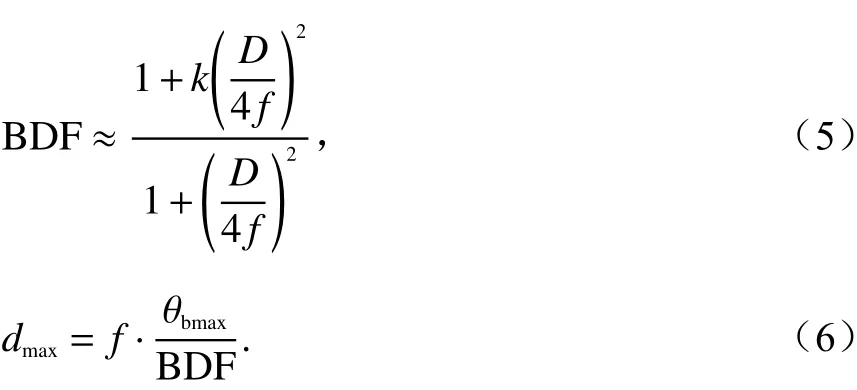
根据焦面场的采样面积和PAF最优单元间距可以计算所需的单元数量. 图13给出了PAF阵列正方形和六边形排布的示意图，图中黑色正方形表示二维扫描波束对应的焦面场轮廓，边长为图中的de为最优单元间距，排布方式不同时de的取值是不同的，应按照图6和图10确定. 阵列中间一行的单元数量为

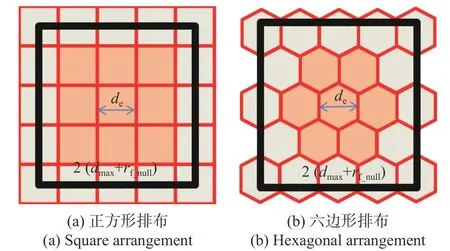
图13 PAF阵列排布示意图Fig. 13 PAF array layout diagram

式中，[x]表示取x的整数部分. PAF整个阵列的单元数量为

2.4 PAF参数选取原则

根据上面的研究结果，PAF参数选取原则总结如下：

1) 焦径比和采样范围. 根据工程中天线口径效率和扫描范围或者视场的要求，由图11确定天线的焦径比和PAF的采样范围.

2) 排布方式和单元间距. 根据焦径比和采样范围，由图6和图10确定PAF的排布方式和单元间距，选择最优单元间距较大的排布方式，此时对应的单元数量更少，性价比更高.

3) 单元数量. 通过式(6)计算对应焦面场的大小，然后根据上面确定的单元间距，通过式 (8)计算整个阵列所需的单元数量.

3 PAF设计和仿真验证

下面给出一个C频段9 m抛物面天线PAF馈源设计实例，天线主要技术指标如表1所示.

表1 9 m天线主要技术指标Tab. 1 Performance specifications for the 9 m antenna

根据天线主要技术指标和本文的PAF参数选取原则，介绍PAF的设计和天线的仿真性能.

首先确定天线的焦径比. 通常边缘两个波束交叠处的增益最低，4 GHz时，假设波束−3 dB交叠，则每个波束的效率需大于88.58%，不容易实现；假设波束−2 dB交叠，每个波束的效率需大于70.36%，比较容易实现. 扫描角度5倍HPBW(4 GHz)到9倍HPBW(7 GHz). 根据图11，焦径比取0.5，PAF采样焦面场第二零深以内区域时，天线口径效率大于70%的最大扫描角度为7.2倍HPBW，口径效率大于60%的最大扫描角度在10倍HPBW以上，可以满足上述要求.

根据图10的结果，六边形排布的PAF最优单元间距比正方形大，所需单元数量少，因此PAF设计采用六边形排布方式；按5.5 GHz中心频率确定单元间距，de=0.42λ/sin θ0=28.6 mm，根据式 (8)，单元数量N=109，其中19个单元合成一个波束. 单元采用方波导，内部填充介电常数为3.6的介质.

图14给出了CST仿真软件中建立的PAF模型，其中红色六边形框分别标注了轴向波束和边缘波束对应的19个单元. 将采用CFM法计算的阵列激励系数代入CST，得到阵列合成方向图，最后将阵列方向图导入GRASP照射反射面天线计算天线性能. 图15给出了阵中单元的驻波性能，可以看到，单元在工作频带内的驻波比小于1.6，而且除了阵列边缘处的单元1、6外，其他单元的驻波比都小于1.5.

图14 PAF的CST仿真模型Fig. 14 PAF model in CST

图15 阵中单元驻波比Fig. 15 VSWR of elements

天线的性能如图16和表2所示. 图16给出了天线分别在低、中、高三个频率的扫描方向图. 当轴向波束的19个单元工作时，其他位置的单元激励系数为零，此时反射面天线的波束指向0°；当边缘波束的19个单元工作时，其他位置的单元激励系数为零，此时反射面天线的波束指向为2.85°. 表2给出了天线在扫描范围内各频点的口径效率和最低增益，轴向波束的口径效率大于72%，边缘波束的口径效率大于51%，最低增益大于48 dBi，满足指标要求. 因此，根据本文焦面场采样方法选取PAF的设计参数是可行的.

图16 天线方向图Fig. 16 Antenna pattern

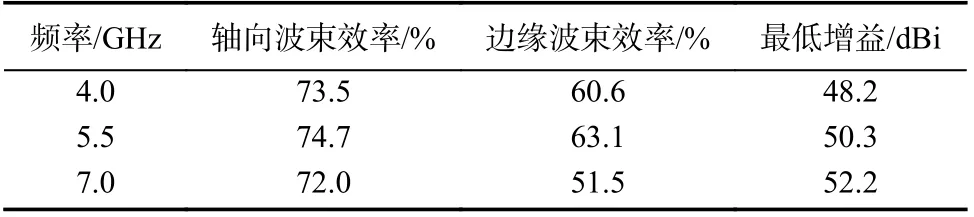
表2 天线各频点的口径效率和最低增益Tab. 2 Aperture efficiency and minimum gain at each frequency point

考虑到成本问题以及馈源对反射面的遮挡，在满足指标要求的情况下，PAF的规模一般设计得尽可能小. 由于边缘波束对应的焦面场出现散焦情况，部分能量扩散到采样区域以外，所以上述边缘波束的口径效率相比轴向波束低了10%～20%，边缘波束的效率可以通过增加单元数量进而扩大采样范围来提升. 图17给出了7 GHz时将合成一个波束的单元数量增加至37个单元后天线的方向图. 可以看出，通过增加单元数量，增大PAF的采样范围，天线的增益明显增高，边缘波束的效率由51.5%提升至56.2%.

图17 单元数量对7 GHz边缘波束方向图的影响Fig. 17 Effect of element number on edge beam pattern at 7 GHz

采用介质填充波导单元的PAF作馈源时，天线的口径效率相比理想波导情况低了10%，这主要是由于阵中单元之间互耦引起阻抗失配造成的. 图18给出了单元间互耦对天线方向图的影响，此时无互耦的计算条件是将单元方向图、激励系数和单元坐标输入到GRASP软件计算得到PAF方向图照射反射面天线，不考虑单元之间的互耦. 可以看出，不考虑互耦的情况下，天线的增益明显增高，5.5 GHz时轴向波束的增益由53.0 dBi提高到了53.6 dBi，此时效率为84.6%，7 GHz时边缘波束的增益由53.5 dBi提高到了54.2 dBi，此时效率为60.5%，与采用理想波导得到的结果是一致的.

图18 单元间互耦对天线方向图的影响Fig. 18 Effect of mutual coupling between elements on antenna pattern

4 结 论

本文通过对反射面天线焦面场的分析，研究了PAF设计参数的选取方法，给出了PAF最优单元间距与焦径比的关系曲线，导出了PAF单元数量的计算公式，可以由反射面天线焦径比和需要的视场大小或波束扫描范围确定PAF初始参数. 给出了一个9 m多波束天线C频段PAF设计实例，天线在−3°～3°的扫描范围内口径效率大于51%，最低增益大于48 dBi，满足指标要求，验证了本文分析与初步设计的正确性，可用于指导PAF的工程设计.