基于改进鸡群优化算法的食品拣取机器人路径规划
2022-03-09刘芙
刘 芙
陈宏明2
(1. 江苏省淮阴商业学校,江苏 淮安 223003;2. 淮阴工学院,江苏 淮安 223003)
随着机械工业技术的快速发展,机器人在食品自动化分拣领域得到了广泛应用[1],有效改变了传统人工分拣效率低、强度大、易损耗的缺陷[2]。运用移动机器人对存放在不同点位上的食品原材料进行高效拣取,是食品企业节约成本、提高效益的重要研究方向[3]。
当前,关于食品拣取机器人自身涉及的技术研究较多,但是对多点位食品分拣领域的研究相对较少。余晓兰等[4]对食品分拣机器人视觉技术进行研究,提出了一种改进BP神经网络的伺服控制方法,该方法能够以较快速度将机器人带到预定位置;张好剑等[5]对生产线单个点位分拣路径规划问题进行研究,提出了一种基于改进遗传算法的分拣路径优化方法,提升了分拣效率,但是改进遗传算法收敛性能和运算效率值得进一步研究;Vafadar等[6]考虑机器人最小移动次数和最小姿态变化,提出了一种最优路径规划方法,仿真试验证明了该方法的有效性,但是该方法忽略了抓取点位物品空间位置信息;郝琳等[7]对食品分拣控制系统进行研究,设计了一套包含机器人、工业相机等设备的分拣系统,试验结果也证明了该系统具有较好的稳定性。
研究拟以移动机器人在多工位食品拣取中的应用为研究背景,提出基于改进鸡群优化算法[8](Improved Chicken Swarm Optimization,ICSO)的食品拣取机器人路径规划方案,通过构建多工位食品拣取机器人路径规划双层模型,并设计改进的鸡群优化算法对双层模型进行求解,优化食品拣取和机器人移动路径,以期缩短移动路径,提升食品拣取效率。
1 食品拣取机器人路径规划模型构建
1.1 食品拣取机器人工作流程
以某大型食品加工企业为例,存在多个食品原料供应商,该企业根据产能、移动机器人装载量等因素,将食品原料存放仓库划分为多个大小相等的区域。在每个存放区域内,为供应商指定食品卸载点工位,并设置工位开放权限,只有供应商获得该区域对应工位权限后,才能卸载食品原材料。为便于食品拣取规划化、流程化管理,企业为供应商提供不同大小的食品箱,供应商根据食品原材料特性放置于不同型号的食品箱内,并将食品原材料信息录入对应食品箱电子标签中,供应商到达存放仓库后,按照权限,依次填满每个存放区域内对应工位。一个食品拣取移动机器人对应一个或多个食品存放区域,当食品存放区域所有工位满载时,移动机器人按照路径规划方案,依次拣取所有工位上的食品。每个存放区域食品清空后,对供应商开放权限,进入下一轮食品拣取流程,图1为食品拣取机器人工作示意图。
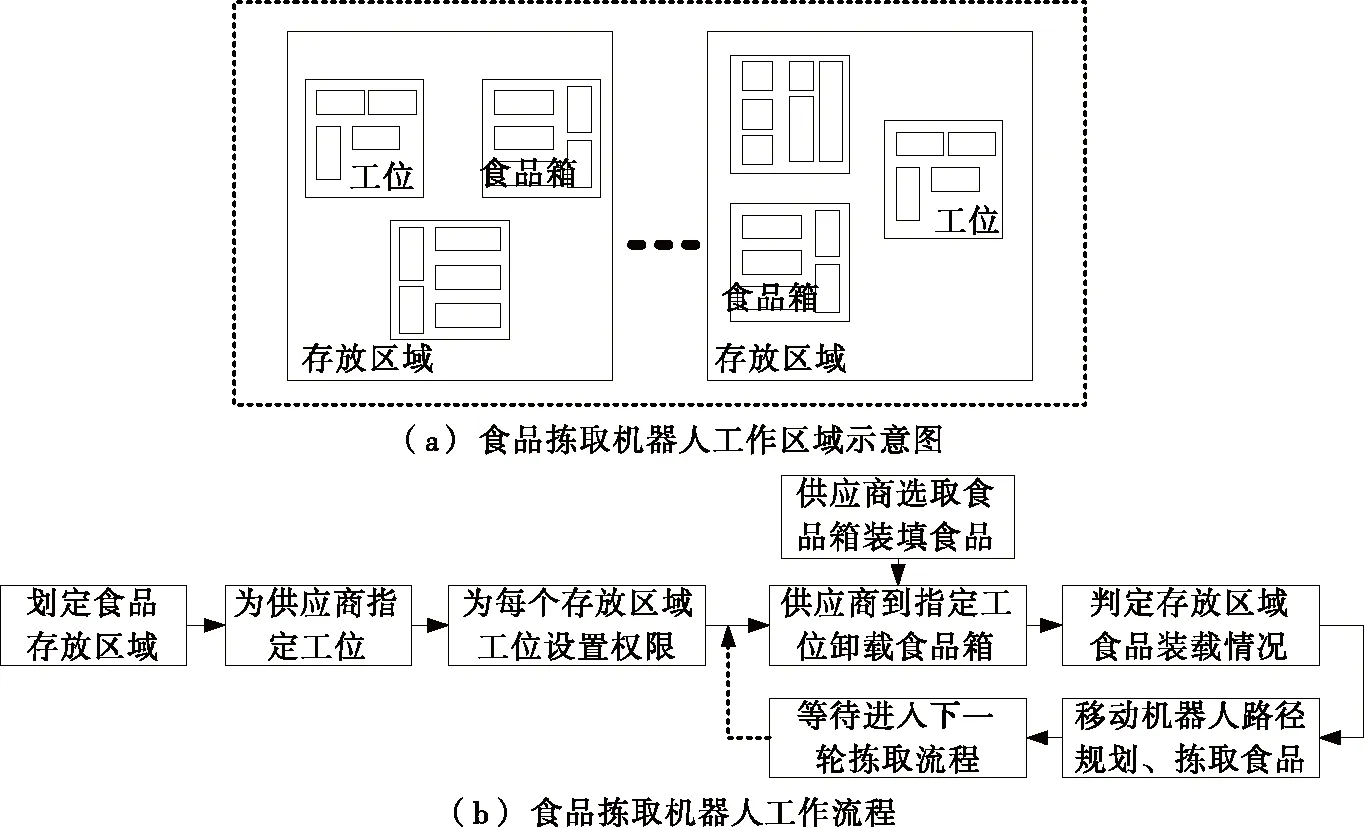
图1 食品拣取机器人工作示意图Figure 1 The working diagram of food picking robot
1.2 路径规划模型构建
以某个食品原材料存放区域满载为例,建立单个工位机器人最优拣取位置和多工位机器人移动最短距离双层路径规划模型。


图2 食品拣取机器人路径规划示意图Figure 2 Path planning diagram of food picking robot

(1)
式中:
Li——第i个工位机械臂从抓取到放置所用总路径;

d(a,b)——两点间的距离。

(2)
从式(2)可知,不同的作业点位,其作业总路径也是不同的,采用鸡群优化算法对第i个工位的最佳作业点位Pbest,i(xbest,i,ybest,i)进行求解,进而得到第i个工位的
最佳抓取路径Li,best:
(3)
1.2.2 多工位机器人移动最短距离模型 机器人需要游历遍N个工位,移动过程中尽可能选择最短移动距离的同时也需要规避障碍物,为此将机器人在工位间的路径规划划分为两个阶段,第一阶段,将机器人游历{(xbest,1,ybest,1),…,(xbest,N,ybest,N)}过程等效为经典旅行商问题(Traveling Salesman Problem,TSP)[9-10],采用鸡群优化算法对该问题进行求解,得到机器人访问工位序列{(x1,y1),…,(xN,yN)};第二阶段,对两工位间机器人移动路径进行规划,建立如图2(b)所示的路径规划模型:在点Pi=(xi,yi)和点Pi+1=(xi+1,yi+1)(i=1,…,N-1)间找到M个节点(k=1,…,M)L,依次连接Pi、X1、…、XM、Pi+1,得到机器人移动路径Z(Pi→Pi+1):
Z(Pi→Pi+1)=Z(Pi,X1,…,XM,Pi+1)。
(4)

r=d(Pi,Pi+1)/(M+1)。
(5)
在极坐标空间内依次选取M个点Xi(ρi,θi),其中ρ=ir(i=1,…,M)、θ随机设定,这M个点位即为机器人移动路径Z(Pi→Pi+1)内的节点,Xi(ρ,θ)到二维平面坐标系Xi(xi,yi)转换公式为:
(6)
式中:
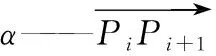
联立式(4)~式(6),可以得到Z(Pi→Pi+1)的长度:
(7)
只需要得到(θ1,…,θM)就可以得到LPi,Pi+1,因此,两点间机器人路径规划问题转化为求解最短路径问题:
(8)
s.t.X1,…,XM∉W1,…,WM。
(9)
式(9)为式(8)的约束条件,即Z(Pi→Pi+1)上的所有节点不在任一食品放置区域内,保障了机器人能够避开障碍物。采用鸡群优化算法对式(8)优化问题进行求解,从而得到两工位间机器人最佳移动距离。
2 路径规划模型求解
2.1 改进鸡群优化算法
鸡群优化算法(CSO)隶属于智能启发式计算技术范畴,其在解空间内初始随机部署一定规模的种群,种群内个体相互间通过协同信息交流完成迭代更新,个体在解空间内分布越广泛、种群多样性越高,算法找到全局最优解的可能性就越大。为此,提出改进鸡群优化算法(ICSO):采用密度峰值聚类算法(density peak clustering,DPC)对种群进行聚类分析,在此基础上将种群划分为不同子种群,并设计新的个体更新进化机制(CSO基本原理不在此赘述)。
2.1.1 DPC种群进行聚类分析 DPC是2014年才被提出的一种新的聚类算法,研究[11-14]表明,该算法对任意数据都有良好的适用性。对于包含Q个个体的CSO种群,采用DPC对CSO种群{X1,…,XQ}进行分析,对于个体Xi,如果其局部密度ρi高于周围其他个体,且具有较大最近点距离δi,DPC则认为该个体为潜在的聚类中心:
(10)
式中:
dij——Xi与Xj的距离;
dc——人为设定的截断距离。


(11)
式中:
Xbest——种群目标函数值最优个体。
(12)
式中:
Xmin、Xmax——个体空间极限。
(13)
式中:
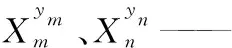
从式(11)~式(13)可以看出,公鸡个体反向进化,增加了算法跳出局部极值的概率;小鸡直接优秀个体进行学习,加速了算法收敛速度;母鸡选择与自己空间差异性较大的个体进行信息交互,扩展了种群搜索空间,使得算法收敛精度更高。
2.2 路径规划实现
2.2.1 单工位最优拣取位置模型求解 每个工位上、下、左、右4个区域为机器人潜在的作业区域,为提高算法运行速度,可以采用信息传递接口(Massage Passing Interface,MPI)并行框架[15-17],每个线程执行一个方位的最佳位置求解进程,最终获得单工位最优拣取位置(xbest,i,ybest,i)。对于单工位最优拣取位置模型求解问题,定义种群个体编码为X=(xr,i,yr,i),目标函数f(X)定义为:
(14)
ICSO循环迭代进化,最终得到每个工位的最优拣取位置Pbest,i(xbest,i,ybest,i)和最佳抓取路径Li,best。图3(a)给出了ICSO优化单工位最优拣取位置流程图。
2.2.2 多工位机器人访问顺序模型求解 对于多工位机器人访问顺序优化问题,定义种群个体编码为X=(x1,…,xN),其中xi=1 or 2…orN、xi≠xj(i,j=1,…,N),若xi=K(K=1,…,N),则表示机器人第i个顺位访问第K个工位。目标函数f(X)定义为:
(15)
从个体编码可以看出,多工位机器人访问顺序优化问题为离散优化问题,若仍采用连续进化方式,会产生大量不符合要求的解。为此,对于个体Xi,若选取Xj为学习进化对象,则个体进化机制定义为,随机选取Xj内β个编码位替代Xi内对应编码位,并将Xj内剩余编码位内编码随机相互调换后,替代Xi内相应编码位,该过程描述为:
Xi,new=β(Xj→Xi)
(16)
式中:
βmax、βmin——最大值和最小值;
Tmax——最大迭代次数;
λ——比例系数且0≤λ≤1。
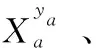
(17)
(18)
(19)
ICSO循环迭代进化,最终得到最优工位访问顺序Xbest=(x1,best,…,xN,best),图3(b)给出了ICSO优化工位访问顺序流程图。
2.2.3 工位间路径规划模型求解 对于工位间路径规划优化问题,定义种群个体编码为X=(θ1,…,θM),目标函数f(X)定义为:
(20)
式中:
d(pi,pM)——式(4)~式(7)列举的移动路径内节点。
ICSO循环迭代进化,最终得到工位间最优路径{Lx1,best,x2,best,…,LxN-1,best,xN,best,LxN,best,x1,best},图3(c)给出了ICSO优化工位间路径规划流程图。
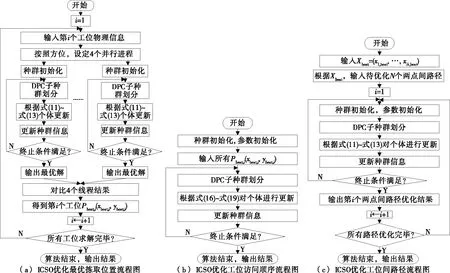
图3 食品拣取机器人路径规划实现流程图Figure 3 Implementation flow chart of path planning of food picking robot
3 仿真试验与结果分析
3.1 验证试验
以某食品加工生产企业为例,每个存放区域为80 m×80 m正方形区域,某个存放区域设定6个工位,每个工位边长10 m,设定食品箱规格为1.2 m×0.8 m、0.9 m×0.6 m、0.5 m×0.5 m 3种类型,供应商根据原材料特性,选取食品箱类型,并装载到指定工位。该存放区域在坐标(28,40)、(50,40)、(25,23)处有3个半径为3 m的圆形立柱,存放区域工位空间信息及ICSO参数设置如表1所示。

表1 工位空间信息及ICSO参数设置Table 1 Station space information and ICSO parameter setting
采用ICSO算法对食品拣取机器人路径规划进行求解,图4给出了ICSO优化单点位拣取最优位置(以第1个工位为例)、工位访问顺序和两工位间路径规划(以第1工位到第2工位间移动路径为例)函数收敛曲线,图5给出了食品拣取机器人路径规划结果,表2给出了路径规划具体参数结果。

图4 ICSO函数收敛曲线Figure 4 ICSO function convergence curve

图5 ICSO优化食品拣取机器人路径规划结果Figure 5 ICSO optimized path planning results offood picking robot
从仿真结果可以看出,研究提出的基于ICSO的双层路径规划方案能够找出每个工位最佳拣取位置,得到的移动路径最短,而且能够避开障碍物。此外,从表2可以看出,每个工位机器人移动机械臂总移动距离达到了150 m 以上,接近了机器人总的移动距离,可见,对每个工位抓取距离进行优化,能够提高机器人食品拣取效率。

表2 路径规划具体参数结果†Table 2 Specific parameter results of path planning
3.2 对比试验
为进一步验证所提方案有效性,设定存放区域为300 m×300 m正方形区域,并将区域均等划分为边长20 m×20 m的225个网格,随机选取每行内2个网格为工位,共计30个工位,工位区域边长仍为10 m×10 m。采用基本CSO算法、布谷鸟算法(Cuckoo Search Algorithm,CSA)[18]、细菌觅食算法(Bacterial foraging optimization algorithm,BFOA)[19]以及文献[20]提出的路径优化方案进行对比试验,每种算法独立运行30次,结果取均值。图6给出了4种算法函数收敛曲线,表3给出了路径规划具体参数对比结果。
从图6可以看出,对于单工位最优拣取位置、多工位访问顺序以及两工位间路径规划问题,ICSO无论是收敛精度还是收敛速度都要优于其他3种算法,这是因为,采用DPC对种群进行聚类分析,个体在选取学习进化对象时更有针对性和合理性,而且为公鸡、母鸡、小鸡分别设计不同的进化公式,兼顾了收敛速度和收敛精度,使得ICSO具有更好的全局寻优能力。从表3可以看出,无论是在移动距离还是在周期运行时间上,基于ICSO的路径规划方案优于其他4种方案,总路径缩短了7.3%~16.7%,运行时间减少了8.14%~39.33%;文献[20]所提方案性能次之,基于CSO的方案表现最差,表明提出的基于改进鸡群优化算法的食品拣取机器人路径规划方案能够给出合理的食品机器人拣取路径规划方案,提高了食品分拣机器人路径规划效率,具有较好的实际应用价值。

图6 4种算法优化食品拣取机器人路径规划结果Figure 6 Path planning results of food picking robot optimized by four algorithms
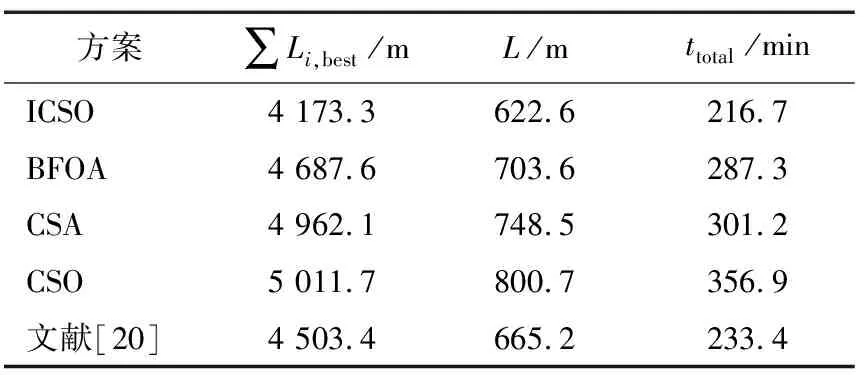
表3 不同方案路径规划参数结果Table 3 Path planning parameter results of different schemes
4 结束语
对食品拣取机器人路径优化问题进行研究,提出了基于改进鸡群优化算法的路径规划方案,通过建立双层路径规划模型,利用密度峰值聚类算法对种群聚类分析,重新定义个体编码方式和更新机制,提升了改进鸡群优化算法的全局优化能力,最后采用改进鸡群优化算法对双层模型进行求解,得到的路径规划长度更短,运行效率更高。下一步将结合物联网技术,动态实现机器人食品拣取路径规划研究。
