半空间近场声全息技术的等效源配置研究

景文倩

（湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室，湖北 襄阳 441053）

近场声全息技术[1–5]（Near-field acoustic holography，NAH）是一种有效的声场可视化和声源定位工具，因此得到很多研究学者的青睐。从空间傅里叶变换方法到逆边界元方法、最小二乘法、统计最优法和等效源法，NAH技术的全息变换算法一直在持续发展和完善。然而，应用这些算法的前提是全息数据必须在一个自由声场环境中获取。事实上，大多数振动体可能被固定在某一边界面上，或位于边界面上方，导致自由空间声场变成半空间声场，此时由边界面产生的反射声对空间声场的影响应当予以考虑。

由于声场分离技术[6–8]可以分离传入波和传出波，因此可用来重建半空间声场。而且该技术有一个明显优势，即不需要知道反射面的表面声阻抗。但该技术应用于半空间声场时要求测量面必须是包络振动体的封闭面，以确保反射声刚好从测量面的另一侧传播至待研究的半空间声场。此外，该技术本身对测量面也有诸多要求，比如双面声压测量[6]、双面质点振速测量[7]，或单面声压-质点振速测量[8]，需要高额的测量成本，包括测量设备等经济成本和测量工作等时间成本。

如果反射面的表面声阻抗已知，可通过将半空间格林函数引入传统近场声全息技术[9–10]，来实现半空间声场重建。目前有两类半空间格林函数：一类基于平面波假设[9]，认为被反射的声波是平面波，在振动体与反射面距离不够远的情况下半空间声场重建精度显著降低；另一类基于真实的球面波，自动满足反射面的边界条件，可获取较高的半空间声场重建精度，但因涉及积分运算，计算很耗时[8]。

另一方面，在反射面表面声阻抗未知的条件下，若将因反射面产生的反射声视为由一系列位于反射面下方的等效源辐射所得[11]，那么半空间声场问题将转换成多源自由声场问题，即无需考虑反射面的表面声阻抗，也避免了积分计算，且全息数据只需测量单面声压或单面质点振速即可获取，大大降低测量成本。由于该方法独立于反射面表面声阻抗，且基于等效源方法，故将其命名为I-ESM (Independent-equivalent source method)。ESM 严重依赖于等效源的配置，因此不合理的等效源配置可能显著降低声场重建精度甚至导致重建失效，而目前有关等效源配置的研究主要针对自由空间声场。本文将探索适用于半空间声场的等效源配置方法，尤其是表征反射面作用的一系列等效源的配置方案，通过数值仿真研究和分析，寻找一种合适的等效源配置方案，以保证重建半空间声场时始终获得较高精度。

1 理论基础

根据I-ESM 的思想，如果一个振动体位于某无限大反射面上方时，反射声将被视为由一系列位于反射面下方的等效源辐射所得，那么半空间声场将转化成由振动体本身和一系列表征反射声的等效源组成的多源自由声场。

针对表征反射声作用的等效源，文献[11]介绍了两种配置方式：位于像源内部（IIS，Inside the Image Source）和位于接近反射面的平面（CRP，Close to the Reflecting Plane）。如果采用IIS 配置，则认为反射声由一个与振动体形状相同的声源所辐射，且这个声源与振动体关于反射面对称布置；如果采用CRP 配置，则认为反射声由一个与反射面平行的平面声源所辐射。根据文献[11]，基于IIS 配置的I-ESM始终可以获得较高的半空间声场重建精度，而基于CRP配置的I-ESM却不能保证半空间声场重建精度的稳定性，有时会得到比较糟糕的重建结果。据此，本文将研究基于CRP配置的I-ESM技术，通过研究不同等效源配置方案对该技术重建精度的影响，寻找适用于半空间声场的等效源配置方案。

如果振动体位于某反射面上方时，则声场可以由位于振动体内部的简单源和位于反射面下方的简单源所辐射的声场叠加替代，其原理示意图如图1所示。

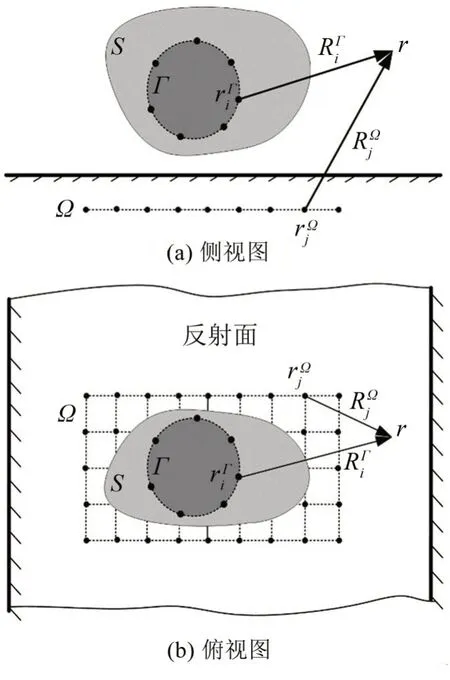
图1 基于CRP配置的I-ESM的原理示意图

给定声场中某点r，则声压可以表示为：

式中：ρ是空气密度，ω是角频率，I和J分别是虚源面Г和Ω上的等效源数目，qΓi和qΩj分别是Г上第i个等效源和Ω上第j个等效源的源强，rΓi和rΩj分别是Г上第i个等效源和Ω上j个等效源的位置。这里gfree代表自由空间格林函数，可表示为：

式中：k是波数，RΓi和RΩj分别是场点r与等效源点rΓi和rΩj的距离。

假定全息面H有M个测量点，则式（1）可以写成矩阵的形式：

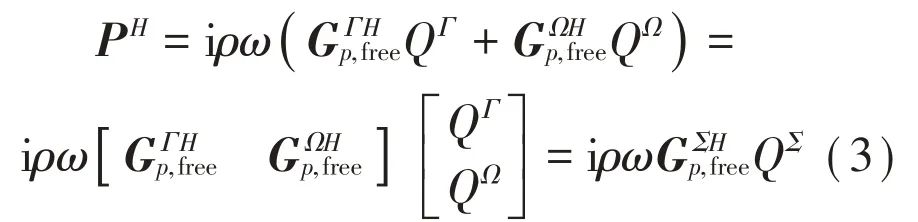
式中：是表征H上声压与Г上等效源之间的声压传递函数矩阵，是表征H上声压与Ω上等效源之间的声压传递函数矩阵，是表征H上声压与Г和Ω上等效源之间的综合声压传递函数矩阵，QΓ=[qΓ1,…,qΓi,…qΓI] 和QΩ=[qΩ1,…,qΩj,…qΩJ]分别是Г上和Ω上的等效源源强列向量，QΣ是Г和Ω上综合源强列向量。根据广义逆矩阵，可得等效源源强列向量QΣ的正则化解为

式中：“H”代表厄密特共轭转置，“-1”代表矩阵逆运算，ε正则化参数，E是单位矩阵。

将求解的等效源源强列向量QΣ的正则解代入式(1)，即可重建半空间声场中任意点处的声压。同时，振动体表面的法向振速也可得到重建：

式中：是振动体表面S上法向振速与Г和Ω上等效源之间的振速传递函数矩阵，表征质点振速传递函数关系，可表示为：

式中：和分别由以下函数组成：

式中：“•”表示点积运算，nS是振动体表面的单位法向量，是振动体表面第n个节点rSn与rΓi之间的距离，是rSn与rΩj之间的距离。

2 基本仿真参数

根据文献[11]，基于CRP 配置的I-ESM 技术不能提供稳定的半空间声场重建精度，有时重建结果很不理想，其最大原因可能是等效源配置不合理，尤其是布置在Ω上表征反射声作用的等效源。本节将研究Ω上的等效源配置对该技术重建半空间声场精度的影响，寻找合适的等效源配置方案，以获得更高更稳定的半空间声场重建精度。

如图2所示，一个半径为0.1 m 的球形声源S位于某反射面上方。假定该反射面是Delany and Bazley 类型[12]，而且拥有无限厚度，那么表面阻抗Z可表示为：

式中：f是频率，σ0是流阻，采用Cgsunits（g∙s-1∙cm-3）。需要注意的是，式(9)未考虑入射角度影响，即该反射面材料属于局部响应。

以球声源S的圆心在反射面上的投影为原点，反射面为xoy平面，建立笛卡尔直角坐标系，z>0 的声场即为待研究的半空间声场，如图2所示。图2很直观地展示了球声源S、全息面H、虚源面Г和Ω在三维空间中的相对位置关系。为了更清晰地说明测量参数和等效源配置参数，又用图3给出仿真示意图的俯视图和侧视图。

图2 声源面S、全息面H、虚源面Г和Ω在三维空间的相对位置示意图

图3 声源面S、全息面H、虚源面Ω的平面位置关系及Ω尺寸和等效源分布间隔

从图3中可以看出，球声源S的球心距离反射面0.5 m，全息面H位于y=0.2 m处。全息测量范围沿x方向上为-0.25 m～0.25 m，沿z方向上为0.25 m～0.75 m，测量间隔沿x和z方向上均为0.05 m。

将声源S均匀离散为42 个节点，在方位角和极角方向的离散间隔分别是π 4 和π 6。表征振动体本身的一系列等效源布置在与球声源S同心的小球面Г上，其球面半径为0.02 m。Г上等效源的分布间隔与球声源表面的节点分布一致。

给定球声源表面的法向振速为：

式中：v0是均匀径向振速，ra是振动球的半径，zS是振动球表面节点的z坐标，za是球心的z坐标。全息声压数据由边界元方法计算得到，其中反射面流阻设置为35 cgs units，并加入信噪比为30 dB 的高斯白噪声。

3 等效源配置讨论

如图3所示，Ω是平行于反射面的平面，其上等效源的配置方案可以从两个方面考虑：

(1)Ω的位置，以相对反射面的后退距离hz表示，依次设置为-0.001 m，-0.2 m，-0.5 m和-1 m；

(2)Ω的大小、等效源分布间隔等，以参数组(x1,x2,y1,y2,dx,dy)表示，共设置18 组，如表1所示。其中，x1和x2分别表示Ω在x方向上的最小和最大坐标值，y1和y2分别表示Ω在y方向上的最小和最大坐标值，dx和dy分别表示等效源在x和y方向上的分布间隔，如图3(a)所示。

分别采用不同后退距离hz和不同参数组(x1,x2,y1,y2,dx,dy)，采用基于CRP 配置的I-ESM技术重建500 Hz时球声源表面法向振速，其重建误差如图4所示。这里，定义法向振速的重建误差为：

图4 不同等效源配置情况下500 Hz时球声源表面法向振速重建误差

式中：VSrecon和VStheo分别是球声源表面法向振速的重建值和理论值。

首先，分析后退距离hz对重建误差的影响。在hz依次取值-0.001 m，-0.2 m，-0.5 m的情况下，当参数组取值相同时，法向振速重建误差随着hz的减小而减小。但当hz取更小值-1 m时，重建误差不再减小，有时反而会增大，比如参数组取第3～10号的情况。因此，Ω相对反射面的后退距离hz应设置为-0.5 m。有趣的是，球声源S刚好位于反射面上方0.5 m 处。由此可认为，Ω应置于声源中心的镜像位置。

其次，分析Ω的大小(x1,x2,y1,y2)和等效源分布间隔(dx,dy)对重建结果的影响。当hz取值-0.001 m，-0.2 m，-0.5 m 时，尤其是取前两个值时，每条法向振速重建误差曲线都有着相同的转折点，如参数组取第3号和7号的情况。从表1可知，这些转折点刚好对应于Ω的大小(x1,x2,y1,y2)改变的情况。而当Ω的大小取值相同时，重建误差随着等效源分布间隔(dx,dy)变化并不明显。由此说明，Ω的大小对重建精度影响比较明显，而等效源分布间隔对重建精度影响甚小。但当hz为-1 m时，也就是Ω远在镜像距离-0.5 m 以外的情况下，不论是其大小还是等效源分布间隔都对重建精度影响很小。基于这些分析结果，下文只考虑等效源分布间隔(dx,dy)均为0.05 m时的等效源配置情况。

然后，分析每条重建误差曲线中的特殊点。当hz=-0.001m 或hz=-0.2 m 时，即Ω在镜像距离-0.5 m 以内，法向振速重建误差分别在参数组取第7 号和第14号时为最小值和最大值。图5给出了由第7号和14号参数组所绘制的虚源面Ω7和Ω14。从图中可以看出，Ω7正好覆盖声源与全息面之间的区域，而Ω14是最大虚源面，覆盖了所有参数组所确定的虚源面。这些结果说明，当Ω在镜像距离-0.5 m以内时，等效源应仅布置在声源与全息面之间的区域，可获得较好重建结果。

最后，寻找合适等效源配置。从以上分析可知，后退距离hz设置为-0.5 m 是比较理想的选择，但如果(x1,x2,y1,y2,dx,dy)选取不当，比如选取第14号，则法向振速重建误差甚至可能大于hz取-1 m 时的重建误差。从图4可以看出，在hz=-0.5 m 的情况下，当参数组取第3号、5号、7号、9号或17号时，重建误差都比较小。由第3 号、5 号、7 号和17 号参数组所绘制的虚源面Ω3、Ω5、Ω7和Ω17如图5所示。

图5 虚源面Ω的位置和尺寸示意图

由图可知，Ω3正好覆盖了球声源在Ω上的投影区域；Ω5则稍小，其上等效源都集中分布于球声源中心部分在Ω上的投影区域；Ω17也是覆盖了球声源中心部分在Ω上的投影区域。另一方面，Ω7正好覆盖声源与全息面之间的投影区域，Ω9尽管稍大，但也主要集中在这个区域。总之，Ω上的等效源要么分布在声源中心部分的镜像位置，要么分布在声源与全息面之间区域的镜像位置。

4 合理等效源配置方案验证

基于以上分析，表2给出了3种具有代表性的等效源配置方案。其中，第14 号参数组和hz=-0.001m 代表较差方案，第5 号参数组和hz=-0.5 m代表较好方案，而第1号参数组和hz=-0.2 m则表示中等方案。分别采用3种等效源配置方案重建球声源表面法向振速，重建结果如图6所示。从图中可以看出，由第5号参数组和hz=-0.5 m得到的重建结果与理论值吻合比较好，而由第14 号参数组和hz=-0.001m 得到的重建结果则与理论值偏差比较大。此外，表2也给出了3种等效源配置情况下法向振速的重建误差。不难发现，由第5 号参数组和hz=-0.5 m得到的重建误差很小，而由第14 号参数组和hz=-0.001m 得到的重建误差则大得多，由第1号参数组和hz=-0.2 m 得到的重建误差处于两者之间。这些分析结果表明第5 号参数组和hz=-0.5 m 确实是比较合适的等效源配置方案，同时也说明在等效源配置合理的前提下，I-ESM 将是一种有效的高精度半空间声场重建方法。

图6 频率为500 Hz时球声源表面法向振速的重建结果和理论值.

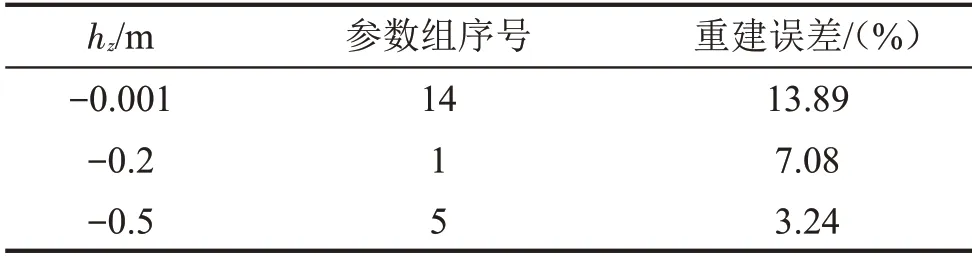
表2 选取3种等效源配置方案及对应的球声源表面法向振速重建误差

此外，图7和图8分别给出了球声源表面法向振速重建误差随着频率和反射面流阻的变化曲线。从图种可以看出，由第5号参数组和hz=-0.5 m得到的重建误差始终很小，由第1号参数组和hz=-0.2 m得到的重建误差稍大，而由第14 号参数组和hz=-0.001m 得到的重建误差则大得多，再次说明第5 号参数组和hz=-0.5 m 是比较理想的等效源配置方案，而且合适的等效源配置方案可以为I-ESM 提供更高更稳定的半空间声场重建精度。

图7 球声源表面法向振速重建误差频响曲线

图8 频率为500 Hz时球声源表面法向振速重建误差随反射面流阻的变化曲线

5 结语

本文针对基于CRP配置的I-ESM技术重建半空间声场时精度不稳定问题，探讨适用于半空间声场的等效源配置方法。通过重建球声源表面法向振速，分析得出位于虚源面Ω上表征反射声作用的等效源的合理配置方案为：虚源面Ω应当置于声源的镜像位置，且等效源尽量分布在声源中心部分的镜像位置或分布在声源与全息面之间区域的镜像位置。同时，仿真分析结果也说明合适的等效源配置方案可以保证基于CRP 配置的I-ESM 的准确性，可提供更高更稳定的半空间声场重建精度。

此外，以某双核音箱为实验对象，开展了一系列实验研究，并分别考虑了大理石刚性地面和海绵吸声材料两种反射面。实验结果与数值仿真结果基本一致，即反射声的等效源应尽量分布在真实声源中心部分的镜像位置。受文章篇幅所限，实验研究部分未在本文给出，将分析整理成其他文章。