含间隙多约束碰撞振动系统稳定性分析
2022-03-09丁旺才李得洋
王 超,丁旺才,李得洋,丁 杰
(1.兰州交通大学 机电工程学院,兰州 730070;2.兰州交通大学 材料科学与工程学院,兰州 730070)
含间隙的碰撞振动系统[1-4],广泛存在于车辆、机械等各类工程领域中,由于间隙和各类约束引起了刚度突变,导致系统向量场Jacobi矩阵不连续,从而使系统表现出复杂且丰富的非光滑动力学行为。因此,深入研究该类系统的运动机理,分析参数对系统稳定性的影响,掌握系统的全局性能等具有重要意义。
Lyapunov指数谱是一种判断系统相邻轨道间平均发散或收敛程度的度量工具,用于判定动力系统周期运动稳定性以及混沌运动特性。目前针对Lyapunov指数谱的研究大多基于光滑动力系统[5-6],但由于非光滑动力系统Jacobi 矩阵的不连续性,针对光滑动力系统的计算方法无法适用,因此近年来学者们针对特定的非光滑动力系统也提出了相应的计算方法。文献[7]针对碰撞振动系统,在连续碰撞间引入超越映射计算得到了该系统的Lyapunov 指数谱。文献[8]对单自由度碰撞系统引入局部映射,利用Gram-Schmidt 正交化和范式归一化计算得到了该系统的Lyapunov 指数谱。文献[9]介绍了n维碰振系统Floquet乘子与Lyapunov指数谱的解析关系,并提出了相应的判据。文献[10]针对一类两自由度碰撞振动系统,结合文献[5-6]的方法讨论了系统混沌吸引子与周期吸引子的Lyapunov 指数谱收敛序列。文献[11]研究了一类两自由度含间隙和预紧弹簧的力学模型,结合Lyapunov指数谱分析了系统稳定性,并用测试函数预测了系统发生擦边现象时的参数范围。文献[12]将含间隙碰振系统在碰撞面处转化为离散系统,构建了Poincaré 映射并通过数值仿真对照,验证了其方法的有效性和正确性。文献[13]研究了一种求解大型Lyapunov 矩阵,采用并行预处理的变形共轭梯度法,通过仿真比较,确认了预处理算法显著优于未预处理算法。文献[14]针对两自由度含弹性约束系统,结合Lyapunov 指数谱图、单参分岔图和相图分析了系统周期运动的稳定性及存在的各类分岔行为。文献[15]针对单自由度碰振系统,在多参数协同仿真方法的基础上,结合胞映射法研究了系统在间隙(b1,b2)参数平面内各类周期运动分布及共存的特点,总结了相邻周期运动之间的转迁规律。
已有研究针对系统稳定性分析成果,大多基于同种约束碰撞振动系统。本文以铁路车辆转向架为工程背景,通过对轮对轴承与轴承止挡以及弹性约束的局部简化,得到单自由度含不同约束碰撞振动系统模型,在系统碰撞面处离散化处理,并利用Gram-Schmidt正交化和范式归一化计算得到该系统的Lyapunov指数谱。通过数值模拟分析,结合系统相图、单参分岔图及Lyapunov 指数谱对照分析,讨论系统在单个参数变化下相应的Lyapunov 指数变化情况,通过对本文所示动力系统的力学性能分析,可为后期机械系统的设计阶段把握其振动特性,为全局动力学特性、混沌控制以及鲁棒性等方面的研究提供重要的理论依据。
1 系统的力学模型
考虑图1所示的单自由度含刚性和弹性两种不同类型约束碰撞振动系统。质量为M的振子由刚度为K1的线性弹簧和阻尼系数为C的线性阻尼器相连接,作用在振子M的上的水平力为简谐激振力P1sin(ΩΤ+τ),使振子沿水平方向往返运动。振子M的位移为X,振子左侧固定一个刚性约束,刚性约束与振子的间隙为B1;振子右侧固定一个刚度为K2的弹性约束,弹性约束面与振子的间隙为B2。由于间隙的存在和碰撞的产生,系统会表现出复杂的非光滑动力学行为。
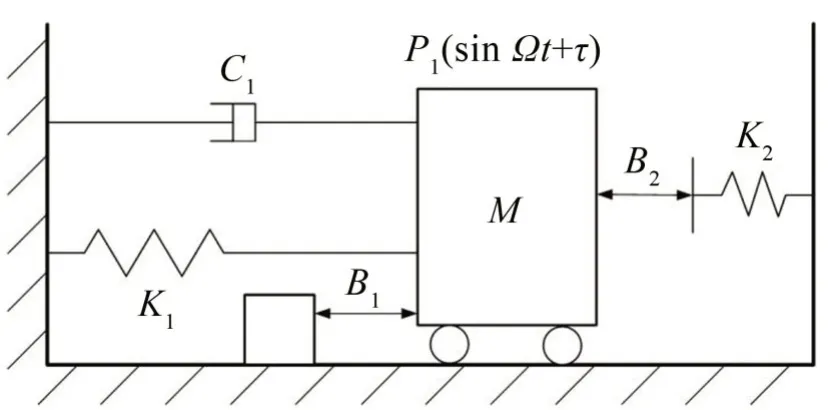
图1 单自由度含不同类型约束的碰撞振动系统
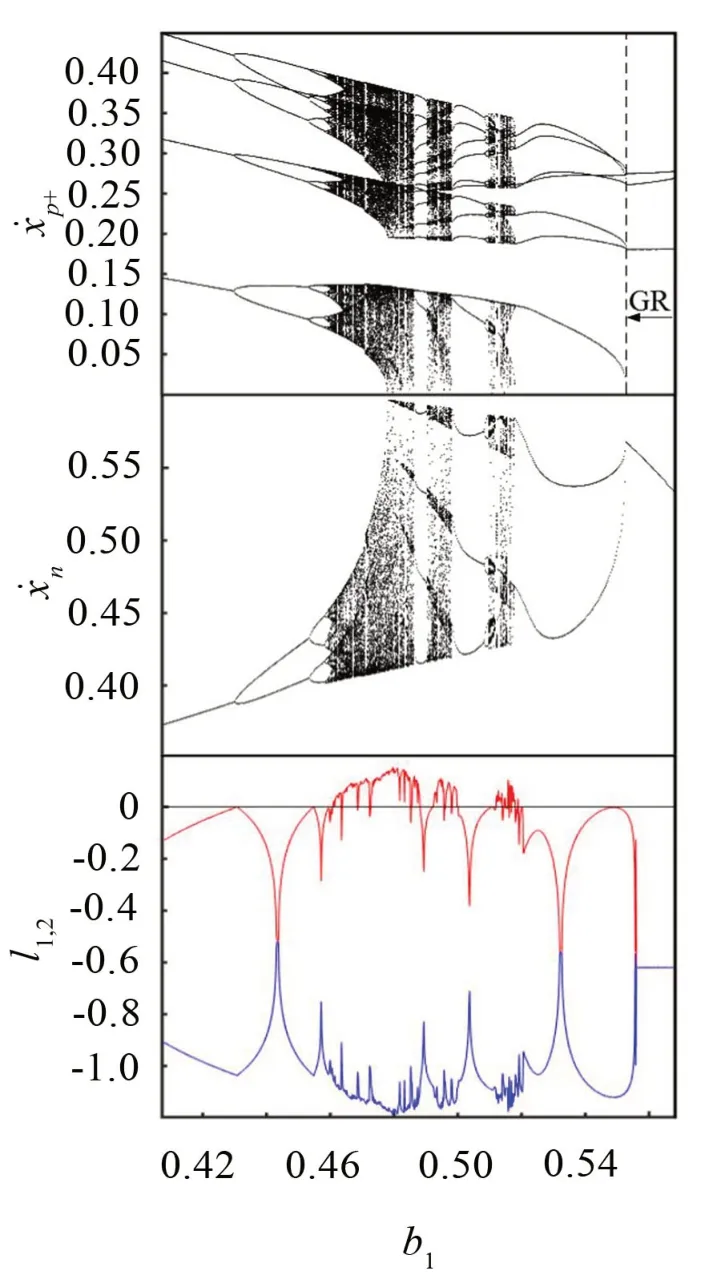
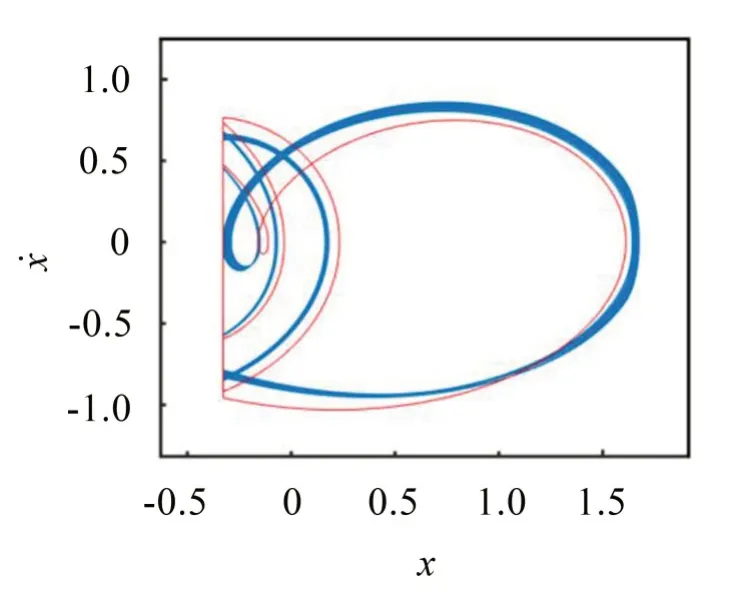
当振子位移-B1 当振子位移X≥B2时,将与右侧弹性约束接触,系统的运动微分方程为: 当振子位移为X=-B1时,将于左侧刚性约束接触,此时满足: 是的,这是杜朗的主意,当罗恬知道赵炎想把家产分给他外面的女人的时候,杜朗帮她精心策划了一场骗局。他假意和陈洋联手谋夺罗恬的财产,其实是要陈洋做替罪羊。一个四处杀人的鬼,是无法结案的,他需要一个活生生的人,让警察捉拿归案。 经无量纲化后,系统无量纲微分方程的通解为: 通过建立Poincaré映射研究系统周期运动的稳定性,Σn,Σp+和Σq+分别代表定相位面、左侧刚性碰撞截面和右侧弹性碰撞截面: 定相位面用于统计系统周期运动的周期数;碰撞截面用于统计振子与左右两侧约束面的碰撞次数,选择截面Σp+建立系统的Poincaré 映射。通过Poincaré 映射的Jacobi 矩阵在不动点的特征值研究系统运动的稳定性及分岔类型。 系统Poincaré 映射的示意图如图2所示。根据接触过程可以将Poincaré映射分为四个阶段:P1:物块与右侧弹性约束面脱离后瞬间到与左侧刚性约束面接触前瞬间的阶段;P2:物块与左侧刚性约束面接触后到脱离前的阶段;P3:物块与左侧刚性约束面脱离后瞬间到与右侧弹性约束面接触前瞬间的阶段;P4:物块与右侧弹性约束面接触后瞬间到脱离前瞬间的阶段。以上4个映射阶段可以表示如下(式中正负号分别代表碰撞后与碰撞前): 图2 系统Poincaré映射示意图 令DP1、DP2、DP3、DP4分别代表P1、P2、P3、P4映射的Jacobi矩阵。对于振子与左侧刚性约束碰撞的阶段,由于瞬时碰撞不改变相位,根据碰撞原理可以得到: 对于非瞬时碰撞的阶段,Jacobi 矩阵DP1、DP3和DP4可按下式计算: 式中:fi表示每个映射的第i个分量;Xj表示每个阶段的初始状态0和τ0。系统每个阶段的Poincaré 映射表示如下: 对式(9)和式(10),利用复合函数求导法则,并运用隐函数定理,可以求得矩阵DPl(l=1,3,4)中的各元素: 系统n-1-1(即t1+t2+t3=2nπ/ω时)周期运动的映射及其对应的Jacobi矩阵可表示为: Lyapunov 指数谱作为判定动力系统稳定性和混沌特性的工具,是根据系统最大Lyapunov指数是否大于零来判定系统处于稳定周期运动状态或混沌运动状态。计算系统的Lyapunov指数谱时,首先选择2 个线性无关的初始扰动(δx(0)1,δx(0)2),定义(μ(0)1,μ(20))=(δx(10)/||δx(10)||,δx(20)/||δx(20)||),以(μ(10),μ(20),)为初始向量,根据式(9)所求的线性化矩阵DP,按δx( k)=DP(x(k-1))⋅δx(k-1)进行迭代一次,可得到一个二维向量(δx(1)1,δx(1)2)。进行下一次迭代前,对此向量采用Gram-Schmidt 正交化和范式归一化处理,将得到的解向量(μ(1)1,μ(1)2)作为初始向量并进行下一次迭代。迭代次数为k时,Gram-Schmidt 正交化和范式归一化处理方法为: 当迭代此时K足够大时,便可得到碰撞振动系统的Lyapunov指数谱为: 考虑系统参数(1):R=0.8、ω=0.5、ζ=0.1、b2=1.396、μk=10,分析图1所示碰撞振动系统的稳定性,文中用n-p-q表示系统周期运动,n表示系统力周期数,p表示振子与左侧刚性约束面碰撞次数,q表示振子与右侧弹性约束面碰撞次数。当系统最大Lyapunov 指数小于0 时,表明相邻轨道间的距离逐渐变小,最终演化为一个点或者一个极限环,此时系统处于稳定周期运动状态。如b1=0.534 6 时,系统处于2-7-2稳定周期运动,周期运动相图如图3(a)所示、周期吸引子分布图如图3(b)所示。为得到Lyapunov指数谱序列,本文采用10 000次迭代,并将前7 000次迭代略去,得到图3(c)所示Lyapunov指数谱序列图,从图中可得出,当系统处于稳定周期运动状态时,它的两个Lyapunov指数均为负值。 图3 2-7-2稳定周期运动 当系统最大Lyapunov 指数大于0,表明从相邻点出发的轨道迅速分离,此时系统处于混沌运动状态。如b1=0.48时,此时系统处于混沌运动状态,系统混沌运动相图如图4(a)所示、混沌吸引子分布图如图4(b)所示。采用相同迭代方法得到图4(c)所示Lyapunov 指数谱序列图,结合图4(c)可知当系统处于混沌运动时,系统两个Lyapunov 指数有一个大于0。 图4 混沌运动 为研究一定范围内系统稳定性,选择系统参数(1)不变,取b1作为分岔参数,取值范围b1∈[ 0.407 8,0.5712 ]。系统左侧刚性碰撞面Σp+、定相位面Σn的单参分岔图以及Lyapunov 指数谱图如图5所示,图中GR表示擦边分岔。 由图5可知,在参数b1由大减小的过程中,系统由1-3-1 周期运动,在b1=0.555 6 处经擦边分岔转迁为2-7-2 周期运动,转迁过程中周期运动相图分别为图6(a)至图6(c),发生擦边分岔时系统对应的Lyapunov 指数会发生跳跃现象;当b1进一步减小,经一系列倍周期分岔进入混沌,此时系统最大Lyapunov 指数大于0,混沌运动相图如图6(d)所示;在b1=0.510 4 处系统由混沌运动退化为3-11-3周期运动;随着b1的进一步减小,在b1=0.500 1处发生鞍结分岔,系统由3-11-3稳定周期运动直接进入混沌,发生鞍结分岔时系统的雅可比矩阵特征值分别为:λ1=1.000 565 81、λ1=0.568 412 59。之后系统经历一个相同序列,由混沌经一系列逆倍周期分岔转迁为稳定周期运动,再由稳定周期运动经鞍结分岔进入混沌,系统由混沌运动经一系列逆倍周期分岔分别转迁为2-8-2周期运动、1-4-1周期运动,周期运动相图分别为图6(e)至图6(f),当系统发生倍周期分岔(逆倍周期分岔)时,系统对应的最大Lyapunov指数为0。参数b1由小增大的转迁方式与b1减小时的转迁方式相图,该参数条件下不存在相邻周期运动间的共存现象,故不再详细说明。 图5 系统单参分岔图及Lyapunov指数谱 图6 系统周期运动相图 选取系统参数(2):R=0.8、ω=0.5ζ=0.1、b1=0.328 2 、μk=10 ,取b2作为分岔参数,在b2∈[ 1.55,1.632 ]范围内双向变化,系统刚性碰撞面分岔图及最大Lyapunov 指数图如图7所示。图中SN表示鞍结分岔,BC表示边界激变,红色曲线表示b2由大减小时Lyapunov 最大指数值,蓝色表示b2由小增大时最大Lyapunov指数值。 图7 系统单参分岔图及最大Lyapunov指数谱 在相邻周期运动相互转迁时,由于发生不同类型分岔的参数点不在同一位置,导致转迁过程不可逆,这样在相邻周期运动转迁过程中就会形成由这两个相邻周期运动稳定共存的多态共存区。当b2由大减小时,系统由1-3-0 周期运动在b2=1.608 3处经鞍结分岔进入混沌,此时系统最大Lyapunov指数值等于0,同时系统映射的Jacobi矩阵特征值λ1=1.000 035 81、λ2=0.154 598 25,之后随着b2减小系统由混沌进入2-7-1 周期运动。当b2由小增大时,系统由2-7-1 周期运动进入混沌,在b2=1.6135 处经边界激变由混沌运动转迁为1-3-0 周期运动,此时系统最大Lyapunov 指数值等于0。由于发生鞍结分岔和边界激变的参数点不在同一位置,这样在b2∈[1.608 3,1.6135]范围内就会由混沌运动与1-3-0周期运动稳定共存。结合Lyapunov指数谱图加以验证,在b2∈[1.608 3,1.6135]范围内减小时系统最大Lyapunov 指数始终大于0,表明系统处于混沌运动状态;在该范围内增大时系统最大Lyapunov 指数始终小于0,表面系统处于稳定周期运动状态。同时结合系统运动相图(图8)也可得出,在同一参数条件下,系统同时存在稳定周期运动(红色曲线)和混沌运动(蓝色曲线)。 图8 周期共存相图 本文以单自由度含不同约束碰撞振动系统为研究对象,通过建立系统的Poincaré映射,将系统转换为离散系统,并利用Gram-Schmidt正交化和范式归一化方法,得到了系统的Lyapunov 指数谱,结论如下: (1)利用Lyapunov 指数谱可精确判别系统的稳定周期运动与混沌运动,还可确定发生不同类型分岔时的参数位置。 (2)由于擦边分岔、鞍结分岔和边界激变的出现,导致相邻周期运动相互转迁过程不可逆,从而形成多态共存区,利用Lyapunov指数谱可甄别多态共存区中的混沌运动与周期运动。 (3)在间隙b1和b2变化的过程中,两侧间隙分别增大时系统都会由稳定周期运动经历一系列倍周期分岔进入混沌;当b1减小时系统会由稳定周期运动经一系列不稳定擦边分岔进入混沌,当b2减小时系统会由稳定周期运动经鞍结分岔直接进入混沌,并且会导致由稳定周期运动与混沌运动共存的多态共存区。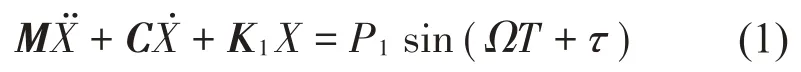
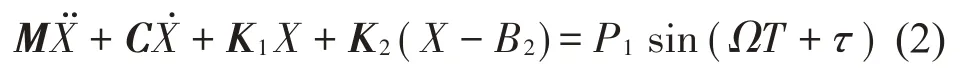


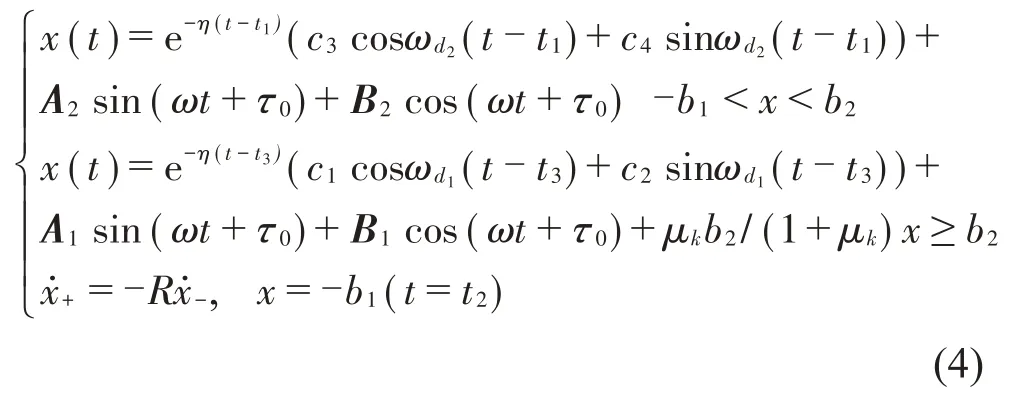
2 Poincaré 映射及Lyapunov 指数谱计算


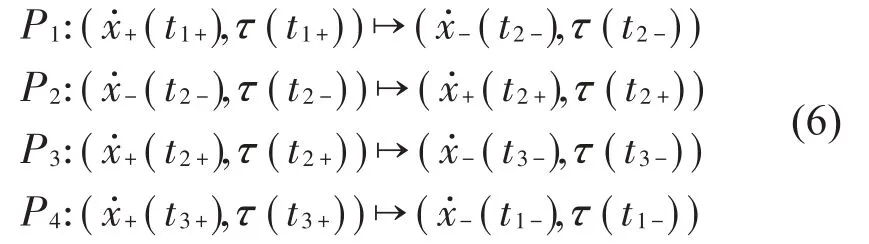

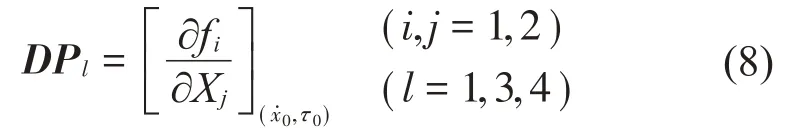


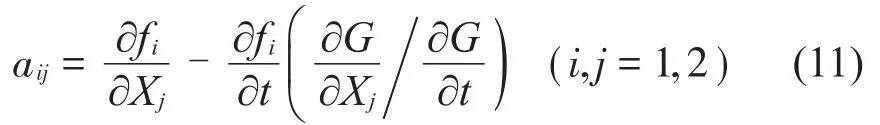
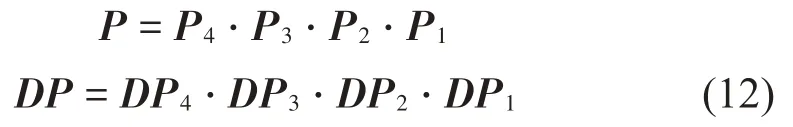

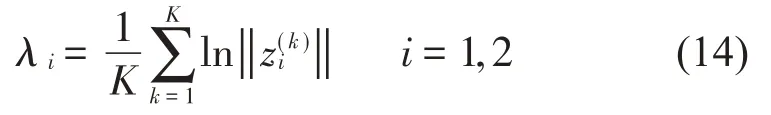
3 系统周期运动仿真与分析




4 结语
