数控机床电机-斜齿轮齿条耦合进给系统动态特性分析
2022-03-09龙新华杜家楠
王 昊,龙新华,杜家楠
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
数控机床是制造业的基石,是表征一个国家制造业水平的重要标志,而其中进给系统的精度问题更是很大程度上决定了数控机床的加工精度,一直是学术界、工业界研究探索的重点。依据进给系统是否运行在有负载的工况,可以将进给系统的运行精度分为静态精度和动态精度两类。静态精度反映了机床进给系统的固有精度属性,其中包括了进给系统中各零部件的直线度、垂直度等几何精度,国内外众多学者通过多刚体动力学理论,将各进给系统的静态精度转换为刀尖点的加工精度,深入分析了静态精度对机床加工精度的影响[1]。而动态精度是指在实际运动工况下,由于机电特性及负载力等因素导致的进给系统的时变运动特性,这往往决定了待加工件的轮廓精度,具有重要的研究价值。
日本东京农工大学的Sato 等[2]建立了交流伺服电机、滚珠丝杠的简化数学模型,并通过部分模型分析法及频响分析法优化了电机的速度环、位置环参数,搭建了具有较好动态性能的丝杠进给系统。南京工业大学的顾华锋等[3]完成了由同步交流电机驱动,蜗轮蜗杆执行输出的回转系统建模工作,并从时域和频率两个角度分析了系统的动态性能。天津大学的罗茹楠等[4]在考虑丝杠柔性的基础上,建立了刚柔耦合的机电模型,分析了丝杠参数对动态性能的影响。
纵览数控机床动态精度方面的研究,其机械传动部分大多为丝杠或蜗轮蜗杆,齿轮齿条鲜有涉及。但是对于重量大、行程长的大型数控机床如镜像铣床,具有承载能力强、运行平稳的齿轮齿条机构往往是较好的选择,因此很有必要对齿轮齿条进给系统进行深入分析。
本文以斜齿轮齿条进给系统为分析对象,分别建立斜齿轮齿条动力学模型与交流同步伺服电机动力学模型,并以上述模型为基础搭建机电耦合系统,结合进给实验,从时域及频域说明斜齿轮齿条进给系统的动态特性,研究过程与结果可为齿轮齿条进给系统的设计与改进提供参考。
1 斜齿轮齿条传动建模
1.1 斜齿轮齿条传动模型
大型镜像铣床x向进给系统的结构如图1所示。主要由交流同步伺服电机、减速器、负载及斜齿轮齿条构成。电机1作为驱动源,向系统输入驱动力矩,减速器2将电机力矩传至斜齿轮,斜齿轮3因此转动与齿条啮合,又由于齿条固定,斜齿轮会做平移运动从而带动负载4移动。

图1 斜齿轮齿条进给系统
根据图1结构与上述传动过程,采用集中参数法,可将图1进给系统简化成图2所示的动力学模型,建立动力学方程如式(1)所示。

图2 斜齿轮齿条进给系统动力学模型

式中:Tex为电机输入机械系统的驱动力矩,krx为减速器的扭转刚度,crx为减速器的扭转阻尼,ix为减速器的减速比,fnx为斜齿轮齿条的动态啮合力,rgx为斜齿轮的分度圆半径,αn为法向压力角,ksx为齿轮与负载之间轴的支撑刚度,csx为支撑阻尼,flx为负载所受阻力,Jmx为电机转动惯量,Jgx为斜齿轮转动惯量,mgx为斜齿轮质量,mlx为负载质量。
其中,斜齿轮齿条之间的动态啮合力fnx是切向啮合力,其表达式为:

式中:knx为斜齿轮齿条的法向啮合刚度,cnx为法向啮合阻尼,β为斜齿轮螺旋角,enx为斜齿轮齿条的啮合误差。
1.2 斜齿轮齿条啮合刚度
斜齿轮由于螺旋角的存在,导致了其啮合是逐步啮入、逐步啮出的时变过程。本文采用势能法及切片积分法求解斜齿轮系统啮合刚度。
由于齿条的渐开线半径无穷大,出于求解方便,将齿条等效化为与其啮合斜齿轮同等大小的斜齿轮。斜齿轮的弯曲刚度kb、剪切刚度ks、轴向压缩刚度ka、赫兹接触刚度kh求解表达式分别如式(3)、式(4)、式(5)、式(6)所示[5]:

齿轮轮体刚度kf亦是啮合刚度的一部分,根据Sainsot等的研究[6],由式(7)求得:

结合图3,上述刚度求解式中:α′1即为图中的α1(z)为每份齿轮上所受啮合力与齿轮切向之间的夹角,α2为齿轮基圆的半基齿角,v为齿轮的泊松比,E为齿轮的杨氏模量,Lct为啮合接触线的长度,Δz=Lct-cosβb/N 为每片轮齿对的啮合接触线在齿宽方向的投影长度,βb为基圆螺旋角,N为斜齿轮被切分的份数,齿轮轮体刚度中的参数μf、sf、L、M、P、Q可查阅Sainsot 等的研究工作[6]获得。串联式(3)、式(4)、式(5)、式(6)和式(7)的刚度即可求得斜齿轮的啮合刚度。

图3 斜齿轮轮齿悬臂梁模型[5]
文中斜齿轮系统参数如表1所示。

表1 斜齿轮参数
主动轮的移速为50 mm/s,结合表1参数,通过势能法及切片积分法可求出斜齿轮系统的时变啮合刚度,如图4所示。图中,时间区间是一个单齿对的啮合周期,虚线部分是单齿对的啮合刚度,实线部分是一个啮合周期内斜齿轮的综合时变啮合刚度。

图4 动态啮合刚度
为验证上述啮合刚度的正确性,将其平均啮合刚度与机械设计手册中的平均刚度[7]相比较,比较结果如表2所示。
由表2可知,本研究中求得的时变啮和刚度均值与根据机械设计手册求出的刚度均值的误差率仅为1.67%,验证了所求时变啮合刚度的正确性。

表2 平均啮合刚度对比表
1.3 斜齿轮齿条啮合误差
齿轮系统的啮合误差可表示为频率分别是轴频、啮合频率的正弦函数的叠加[8]:

式中:Fp为齿距累计总偏差,f′为一齿切向综合偏差,ωa为轴频,ωn为啮合频率,φa、φn均为初始啮合相位,在本研究中,由于不存在初始相位差,因此均为零。查阅现代机械设计手册[7],根据齿轮系统的六级加工精度,可查知Fp=26 μm,f′=10.24 μm。
1.4 机械系统仿真
式(1)中其余各参数如表3所示,依据式(1)的斜齿轮齿条进给系统动力学微分方程,在Simulink 中搭建与之相应的求解模型,同时为了加快求解速度,将已求解的时变啮合刚度以向量值的方式加入到Simulink 中。设置输入的电机驱动力矩为恒定力矩,值为0.64 N∙m,负载所受力与驱动平衡,采用ode45 求解器进行求解,则负载位移误差如图5所示。

表3 机械参数
由图5可知,当机械系统处于平衡状态时,负载的位移误差是幅值量为微米的周期函数,为研究负载位移中的频率成分,对其做频谱分析,见图6。

图5 机械系统负载位移误差
图6中fa是轴频其值为0.25 Hz,fn是啮合频率其值为7.5 Hz,低频段主要的频率成分是轴频和啮合频率,这与机械系统中的内部激励即时变啮合刚度激励、啮合误差激励中的频率成分一致,说明了内部激励对机械系统输出有直接的影响。

图6 机械系统位移频谱
2 交流同步伺服电机建模
2.1 电机控制模型
本研究中的电机为交流同步伺服电机,该类电机拥有多变量、非线性、强耦合等特点。为便于模型控制,研究中采用矢量控制技术,通过控制同步旋转坐标系下的二维电流矢量来控制电机实际的三项定子电流,从而进一步控制电机的转速[9]。整体的控制模型如图7所示。

图7 交流同步伺服电机控制模型
上述控制过程中,较为关键的两部分是升降维变换与PMSM 输出计算[10]。由三维自然坐标系AB-C 向二维固定坐标系α-β的转换被称为Clark 变化,其变换矩阵为TClark[9]:

由于电机是旋转的,因此二维固定坐标系需乘上以电机转角为变量的旋转矩阵才能得到电机的实时坐标系即二维旋转坐标系d-q,该旋转矩阵TPark[9]为:

式中:θe为电机转子转角。对上述两个变换矩阵取逆,即可得到反方向的变换,即二维旋转坐标系d-q通过T-1Park和T-1Clark变换可得到电机的三维自然坐标系A-B-C。
PMSM 计算即永磁同步电机的输出计算,取电机输出轴为分离体,做力矩平衡分析有:

式中:J为电机输出轴转动惯量,ωm为电机输出轴的转速,Te为电机的电磁转矩,TL为电机输出轴上的负载力矩,B为电机的旋转阻尼。
为简化求解模型,基于二维旋转坐标系d-q对电磁转矩进行分析[9],其求解表达式为:

式中:pn为电机极对数,id和iq分别为二维旋转坐标系d-q下的正交电流,Ld和Lq分别为对应的正交电感,ψf为电机磁链。后续只需将式(12)求得的电磁转矩代入到式(11)中,求解该微分方程即可求得电机的输出转速。
2.2 电机控制模型仿真
本研究中的电机采用的是松下A6系列电机,其具体参数如表4所示。

表4 电机参数
根据电机参数及电机控制模型,搭建相应的Simulink 仿真模块。为测试电机性能,设置工况为初速500 r/min、初负载0.2 N∙m,0.4 s 后转速变为750.73 r/min,0.6 s 后负载变为0.64 N∙m,采用ode45求解器,电机的输出转速、输出转矩如图8、图9所示。
由图8、图9可以看出,电机在控制系统调节下能达到预设目标值即输出转速750.73 r/min,输出转矩0.64 N∙m。并且,在转速及转矩突变时均能在0.05 s内达到预期设定值。同时根据图8可知,当向电机输入500 r/min的阶跃转速信号时,电机转速的最大超调量Mp为2.6%,峰值时间tp为1.3 ms,上升时间tr与调整时间ts均约为20 ms,体现了电机控制模型响应快速、超调量小并且稳定准确的特点。

图8 电机输出转速

图9 电机输出转矩
对处于750.73 r/min 的电机转速曲线进行频谱分析如图10 所示,其中fdx值为150 Hz 是电机基频,并且由频谱图可知存在倍频成分。

图10 电机转速频谱
3 进给系统机电耦合仿真
3.1 进给系统机电耦合模型
结合上述齿轮齿条模型与电机动力学模型,建立机电耦合的斜齿轮齿条进给系统,该系统以电机的输入转速为输入量,以负载移速为输出量,并通过将机械系统中的电机转速与电机所受负载力矩反馈回电机模块,使其构成完整的闭环控制系统,该进给系统模型如图11所示。

图11 进给系统模型
图11中,Ne为电机的输入转速,Te为电机输出转矩,vload为负载移速,ωe为机械系统中的电机轴转速,Tload为机械系统中电机轴所受的负载力矩。
3.2 进给系统机电耦合仿真
在Simulink 中搭建上述进给系统模型,设定电机的转速为750.73 r/min,且考虑负载所受力为摩擦阻力,其大小为313.6 N,采用ode45 求解器求解模型,则负载位移曲线如图12所示。由于电机转速为750.73 r/min,可计算出负载的理想位移速度为50 mm/s,因此在运行10 s 后,负载移动了500 mm 即0.5 m,与图12仿真负载位移一致。

图12 负载位移
将负载指令位移即通过v=0.05 t 算得的位移与仿真位移做误差比较,分别考虑齿轮系统中有、无啮合误差的情况,位移误差曲线如图13所示。
从图13可以看出,由于机电惯性,负载仿真位移始终小于指令位移,且该位移误差量较小约为10-5m。此外,当系统中考虑啮合误差时,系统位移误差的波动幅值较大,表明了啮合误差对系统动态特性有较大的影响。对考虑了啮合误差的系统负载加速度、位移进行频谱分析,如图14、图15所示。

图13 负载位移误差
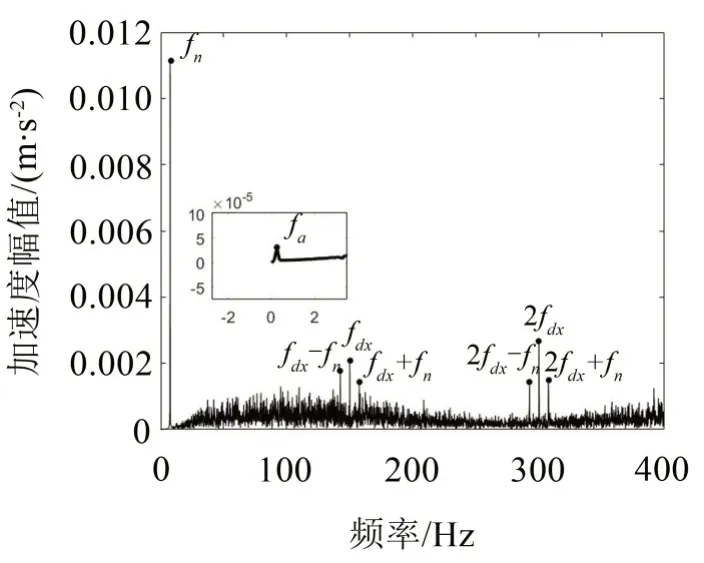
图14 负载加速度频谱

图15 负载位移频谱
由图14 可知,负载加速度频谱中包含了轴频、啮合频率及电机模型中的基频、倍频,同时还存在啮合频率与电机基频、倍频的调频成分,表明了进给系统同时受到电机部分与机械部分的共同影响。此外,根据图15 可知,在负载位移中机械系统的轴频与啮合频率幅值较大,对进给系统的动态特性有重要影响,而电机频率为150 Hz且其幅值在加速度频谱中远小于啮合频率幅值,故在负载位移频谱中电机频率不明显,对进给系统的影响不大。
4 进给系统动态特性实验
4.1 实验系统
实验系统分为三部分,第一部分是实验的研究对象数控机床,其中x向是本文所研究的斜齿轮齿条进给系统,第二部分是机床的控制部分-电气控制柜,第三部分是传递运动指令的上位机,整体实验系统如图16所示。
根据实验系统模型,上位机指令经编码发送至控制器,控制器根据进给系统当前的运动状态进行运动规划与控制,最后将驱动电信号传输至进给系统,使其按规定路径运动。实验实物图如图17所示。

图17 实验系统实物
4.2 实验结果分析
为测试分析机床x向斜齿轮齿条进给系统的动态特性,实验中向上位机输入系统负载移速,同时设置运动终点坐标,使进给系统的负载做匀速直线运动。本实验中,设定系统负载移速为50 mm/s,实验初始坐标为100 mm,终点坐标为400 mm,则负载实验位移与指令位移对比如图18所示。
由图18 可知,由于系统惯性等因素,实验位移曲线落后于指令位移曲线。将指令位移曲线减去实验位移曲线,其位移误差如图19所示。

图18 负载实验与指令位移
图19 表明,在实验运行平稳阶段,负载理想位移与实际位移的误差围绕4.04×10-4m 波动,且波动幅值逐渐减小,运行愈发平稳。与仿真对比,仿真与实验的负载位移均滞后于指令位移,但由于实际制造、安装等误差,实验位移误差的均值大于仿真位移误差的均值。对实验位移滤除直流量后,做频谱分析,如图20所示。

图19 实验位移误差
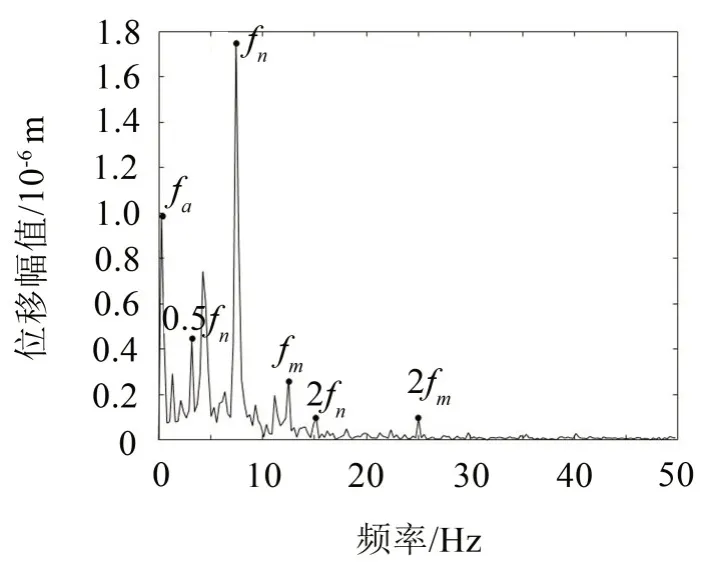
图20 50 mm/s负载位移频谱
从图20 可知,在实验位移中低频部分主要有:轴频fa、啮合频率fn、0.5倍啮合频率0.5fn、2倍啮合频率2fn、电机转频fm和2倍电机转频2fm,其中幅值最大的两个频率为轴频与啮合频率,这与仿真中轴频与啮合频率起主要影响作用的结论一致。
考虑到由于建模中静态啮合误差的轴频幅值系数取的是齿距累计最大误差,根据本文实验结果将其矫正为原先的1/4,使系统中轴频与啮合频率的幅值比与实验结果大体一致,如图21所示。

图21 矫正后的负载位移频谱
本文针对负载移速为30 mm/s、40 mm/s、50 mm/s、60 mm/s和70 mm/s共5种工况各做了10组实验,以30 mm/s 和40 mm/s 为例,分别取其一组实验结果进行频谱分析,如图22、图23所示。

图22 30 mm/s负载位移频谱

图23 40 mm/s负载位移频谱
由图22、图23可知,在30 mm/s与40 mm/s工况中轴频与啮合频率仍是最主要的两个频率成分,对系统的影响最大,这与前文中仿真和实验的结论一致。将30 mm/s、40 mm/s、50 mm/s、60 mm/s 和70 mm/s 一组实验中幅值最大的两个频率列出,如表5所示。

表5 实验幅值最大的两个频率
根据50 mm/s工况下啮合频率的理论值7.5 Hz,轴频的理论值0.25 Hz,可以算得在30 mm/s、40 mm/s、60 mm/s和70 mm/s工况下幅值最大的两个频率均为对应工况下的轴频与啮合频率。
5 结语
本文针对电机-斜齿轮齿条进给系统,考虑时变啮合刚度和啮合误差两部分内部激励,建立了基于矢量控制的机电耦合动力学模型,分析了其动态误差的影响因素,并结合实验进行了验证,结论如下:
(1)齿轮齿条啮合误差是进给系统的动态误差的主要来源,对系统的动态误差起决定性作用;
(2)进给系统动态误差主要的频率成分为轴频、啮合频率、电机的基频、倍频及相应的调频频率,其中轴频与啮合频率占比最大,是最主要的频率成分。
