滚振试验台液压管道系统的振动特性分析

周新建，吕 康,周生通，郭维年

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

液压管道的压力波动容易产生管道的振动，尤其是在高压力波动条件下就更加明显，当液压管道内流体的脉动频率和管道系统的固有频率重合或者接近时，会发生管道系统的共振，从而造成很强的压力波动，严重时将导致管路破裂危及人身安全并造成巨大经济损失[1－2]。国内外以往的研究表明，管内流体-结构相互作用（FSI）会显著影响管道内压力波动，并通过不同的力学过程在管壁产生轴向应力和应变，管道内流体压力产生的周向应变会引起和泊松效应有关的轴向应变[3－4]。因此，在考虑流固耦合作用的情况下，深入研究液压管道的振动特性，对管路系统的设计具有非常重要的意义。

在工程领域中，国内外学者对液压管路的振动机理进行了广泛的探究。Xu 等[5]采用流-热固耦合方法对“L”型热管网络进行了研究，计算了不同条件下实体结构的等效应力，比较了埋入和沟槽条件下耦合和非耦合荷载引起的管网和弯头的受力特性。David 等[6–7]在有压水力瞬变分析中，考虑前两种管道振动模式（即压力波在流体中的传播和轴向应力波在管壁中的传播）进行流固耦合分析。Keramat等[8]对一条有多个轴向支撑的锚固管道进行了室内试验，对采集到的压力信号进行时域和频域分析，破译了由泊松耦合和其他锚效应引起的波动。Hosseini等[9]建立不同类型黏弹性支承的模型，并探讨其对直管水锤作用下流体-结构相互作用（FSI）的影响。周知进等[10–11]利用有限元方法对不同曲率情况下管道的流固耦合特性进行了分析,研究了流固耦合作用对不同曲率管道位置等效应力的影响。Talemi等[12]介绍了微流控二极管的流固耦合（FSI）模拟，利用ANSYS 软件，对襟翼进行三维结构挠度模拟和CFD 交互计算，计算襟翼变形和流场解算器。谢安桓等[13]结合在工程实际中常见的脉动流工况，建立液压管道的流固耦合振动模型，探讨了流体脉动频率以及壁厚等因素对液压管道振动响应的影响。

国内外学者对管道的振动特性进行了广泛的研究，并取得了丰硕的成果；但是，目前利用针对跨座式单轨车辆滚振动试验台的液压激振伺服系统的管路研究，没有相关的报道。本文首先在Solidework软件中建立管道的模型，并将管道模型导入ANSYS Workbench 软件中，将管道的实体和流体区域进行网格划分，分析管道在自由状态、单向和双向流固耦合方法下的模态，得出管道在流固耦合状态下的振动特性，为跨座式单轨车辆滚振试验台的液压激振伺服系统的管路设计和优化提供参考依据。

1 流体运动的数学模型

1.1 流体单元运动控制方程

流固耦合问题是在计算流体力学与计算固体力学快速发展下交叉而生成的力学问题，它由流体运动和固体结构的相互影响，以及流体和固体在运动过程中相互作用所产生的力学相互作用的现象；因此，需要同时满足流体控制方程和固体控制方程进行描述管道系统的流体流动和传热。三维模型的动量和能量方程如下：

能量方程[14]：

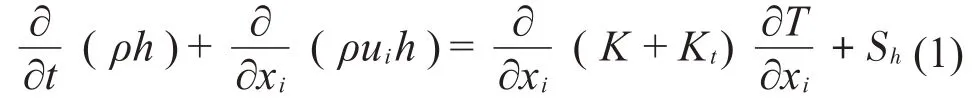
式中：h表示熵，K表示分子传导率，Kt表示由于湍流传递而引起的传导率，Sh表示体积源。

动量守恒方程[15]：

式中：t表示时间，ff表示体积力矢量，ρf的表示流体密度，u表示流体速度矢量，τf表示剪切力张量。

对于密度和黏度不随时间和温度变化的流体，其流体运动满足纳维-斯托克斯（N-S）方程：

式中：t—时间；ρ—流体密度；v—流体速度矢量；F—外力；p—压力；μ—动力黏度。

1.2 管道运动控制方程和湍流模型

对于多自由度的管道系统，其运动状态的有限元方程[16]：

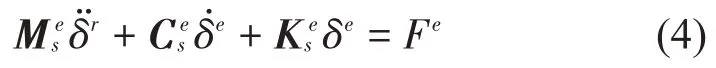
式中：Mes为管道单元的质量矩阵；Ces为管道单元阻尼矩阵；Kes为管道单元的刚度矩阵；δe为管道单元位移矢量；Fe为单元外载荷矢量。

标准的k-ε模型需要求解湍流的动能及其耗散率方程，其湍动能k和耗散率ε的方程如下：

式中：ρ为流体密度；k为湍动能；ε为耗散率；μt为湍流黏度；Gk为平均速度梯度引起的湍动能；Gb为浮力影响引起的湍动能；YM为可压缩湍流中脉动扩张的贡献；C1ε、C2ε和C3ε为经验常数；σk和σε为湍动能k和耗散率ε对应的prandtl数；δk和δε为湍流普朗特数。

1.3 流固耦合方程边界条件

液压管道内流体轴向方向的流动方程：

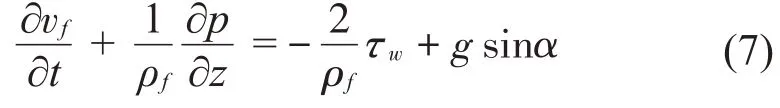
上述方程中，vf—流体流动的平均速度；ρf—流体的平均压力；k—流体的体积模量；τw—管道内部的流体和管道之间的摩擦力。

2 管道的几何模型和理论分析

2.1 单轨试验台和管道的几何模型

跨座式单轨车辆滚振试验台是一种车辆设计过程中用来进行总体型式试验的大型设备，可以在车辆设计过程中验证动态试验条件下的安全性能，如图(1)至图(2)所示，它主要由基座、车体和转向架检修系统组成，其中转向架检修系统包括构架、走行轮、导向轮、稳定轮、基座和液压激振伺服系统；液压激振系统是试验台的重要组成部分，它由液压管道、液压控制元件和液压控制系统等组成。

图1 跨座式单轨车辆滚振试验台概念设计图

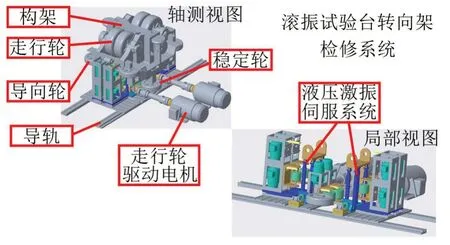
图2 滚振试验台转向架检修系统

根据试验台的设计情况，管道三维模型如图3所示；A 为管道入口，E 为管道出口，管内径为100 mm，管壁的厚度为6 mm，AB=1 200 mm，BC=1 000 mm，CD=6 400 mm，DE=500 mm；管道的材料设置为钢结构，密度为7 850 kg/m3，泊松比为0.3，弹性模量为200 GPa；管内液体材料设置为液压油，密度为0.9×103kg/m3；同时，将管道的三维模型进行网格划分，对管道外部和管道内部的膨胀层分别划分为结构网格和流体网格，流体网格如图4所示。

图3 管道三维模型图

图4 管道内部膨胀层的流体网格

2.2 单向和双向流固耦合的分析方法

单向流固耦合是研究管道内流体对管道结构影响的一种方法，通常忽略管道固体结构对流体的影响，仅将流体计算得到的压力当作载荷加载到管道结构上。双向流固耦合研究的是管道内流体与管道固体结构之间的相互作用，不仅要考虑流体对固体结构的作用，还必须要考虑固体结构对流体运动的影响，需要考虑大变形问题，以及大变形带来的网格变形问题，采用光滑的动态网格并设置管道固体结构与流体之间相互作用的耦合面。本文利用ANSYS Workbench 的Modal、Fluent 和Static Structural等模块，分别对管道的外壁面和流体域（膨胀层）进行单向和双向流固耦合的流体动力学计算，求解管道的模态与振型结果。

3 仿真分析

3.1 不同计算方法下管道的固有频率

当流体压强为2 MPa，进口端流速均为4 m/s，分别对试验台的液压管道自由状态、单向流固耦合和双向流固耦合的模态分析，得到的各阶固有频率见表1；其中，双向流固耦合方法的计算时间设置为10 s，迭代步数为100，间隔时间为0.1 s。

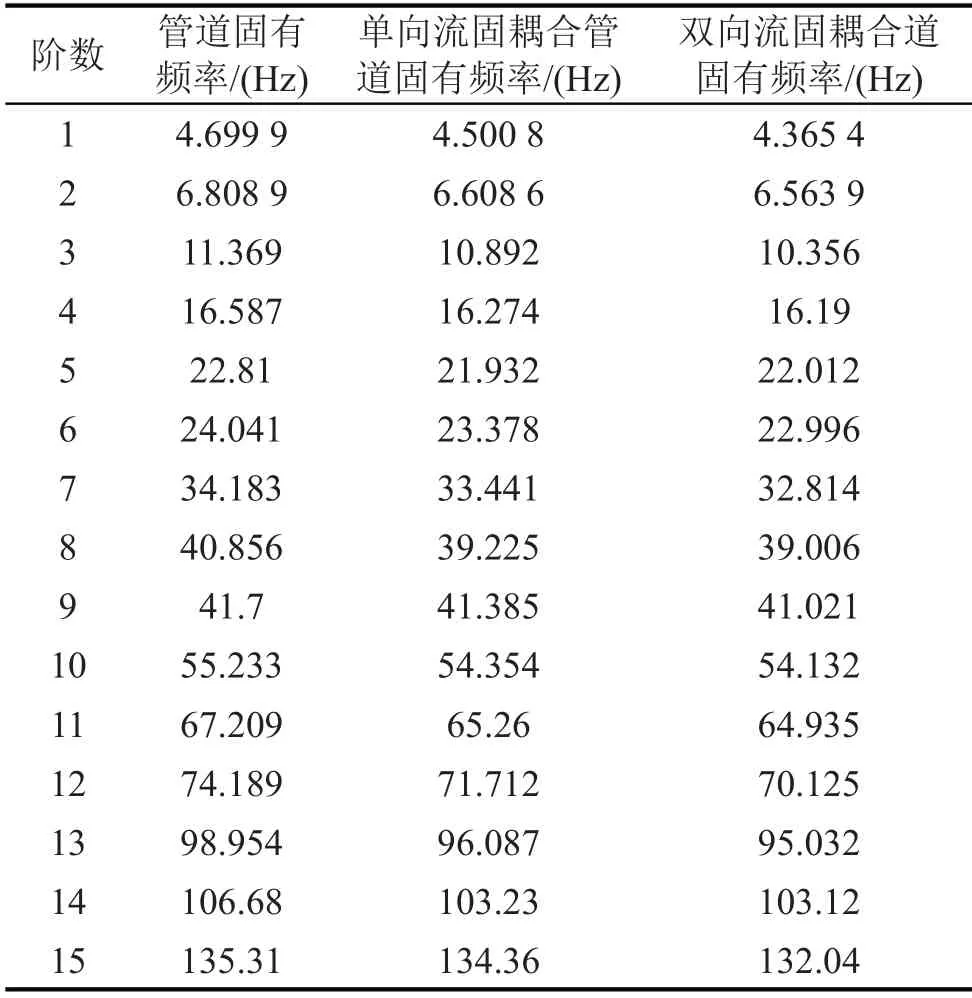
表1 不同计算方式下管道的固有频率

由表1可以看出，管道前6阶的固有频率产生了一些差异，管道在单向流固耦合和双向流固耦合作用下的固有频率小于管道自由状态下的固有频率，误差率达到了2%～10%，可见流体会对管道的固有频率产生一定的影响；同时发现，单向流固耦合的的管道频率都略高于双向流固耦合，可能是因为单向流固耦合只考虑了流体对管道的作用，这样会导致预应力比双向流固耦合作用大。

3.2 单向和双向流固耦合下管道的振型

单向和双向流固耦合作用下的最大振型如表2所示；可以发现，相同阶次下的振型形态基本一致，

表2 单向和双向流固耦合作用下的最大振型

振动幅值略有差异，单向流固耦合的最大振幅均比双向流固耦合大。因此，在分析管道的振动特性时需要考虑双向流固耦合的作用。

3.3 管道内部的流速和压强分布

通过图5和图6可以看出，当管道入口的流速为2 m/s时，采用双向流固耦合方法分析管道内流体速度分布和压强分布情况，管道内的流体速度最大达到了1.185 m/s，水流速度分布较不规则，在管道的CD段出现了垂直于管道向外的速度，管道的弯曲处会出现紊流现象，这是因为流体与固体之间的相互作用力，使管道的部分区域出现了较小的垂直向外的速度；管道内部压力分布较为均匀，但是在CD段出现了局部压力较大的区域，管道内垂直方向的流体在C 点这个位置冲击管道，流体压力与管道壁面之间发生了强烈的泊松耦合效应，导致流体对CD端的管壁作用力变大；从整体看双向流固耦合作用下的的管道压强分布呈均匀分布的态势。

图5 管道内部速度分布图

图6 管道内部压力分布云图

3.4 管道内流体压强对固有频率的影响

利用双向流固耦合方法进行管道模态分析，计算流体压强为2 MPa、4 MPa、8 MPa 和12 MPa 时管道的固有频率，得到不同流体压强的前10阶固有频率如图7所示。

图7 不同流体压强下管道的固有频率

从图7中不难发现，在一定的压强范围内（2 MPa～12 MPa），管道的固有频率随着流体的压强增加而增加[17]，管道内流体压强的增加对管道的固有频率存在一些影响，这是因为随着流体压强的增加，可能会引起管道较大的振动，进而会引起共振，管道的固有频率会随之增大，因此在管道设计的过程中，要充分考虑压强对管道的影响。如图8和表3所示。

图8 流体压强为4 MPa时管道的等效应力图

表3 不同流体压强下的最大总变形和等效应力

从图8和表3中可以看出，在管道拐弯的B点处出现一个高应力区域，流体在此处垂直冲击管道，使流体的运动状态发生了改变，从而导致流体的压力与管壁之间出现强烈的泊松耦合效应，流体在此处与管壁的作用力随之增大；当流体压强为8 MPa时，管道的最大总变形量为3.525 1 mm，当流体压强为2 MPa时，管道的最大总变形量为1.183 1 mm，相当于8 MPa时最大变形量的34%，说明压强的增大，总变形量增大；管道的等效应力也呈现出相同的变化规律。

3.5 管道内流体速度对固有频率的影响

利用双向流固耦合方法进行管道模态分析，计算流体速度为2 m/s、4 m/s和8 m/s时管道的固有频率，得到不同流体速度的前10 阶固有频率如图9所示；从图9可以看出流体速度对管道固有频率的影响并不明显，比压强对管道固有频率的影响小。

图9 不同流体速度下管道的固有频率

从图10 和表4可以看出，在不同流速下管道的总变形和等效应力图存在一些差异，当入口速度为2 m/s时，管道的最大总变形量为0.002 482 9 mm，相当于8 m/s 时最大变形量的24%，等效应力随流体速度变化的趋势与最大变形量类似，随着流体速度的增大，在管道拐弯处B 点容易出现较大的应力和总变形，若此处长时间处于较高的应力状态下，极易发生管道开裂、壁面腐蚀和寿命降低等现象[18]。

表4 不同流体速度下管道的最大总变形和等效应力

图10 流体速度为4 m/s时管道的等效应力图

4 结语

本文基于单向和双向流固耦合的模态分析方法，通过对比分析了管道在自由状态、单向和双向流固耦合作用下的固有频率和振型，研究发现：

(1)单向流固耦合下管道的固有频率均大于双向流固耦合作用下管道的固有频率，相差率达2%～10%，流体会对管道的固有频率产生较大的影响；相同阶次下的振型形态基本一致，振动幅值略有差异，振幅分布位置相似，单向流固耦合的最大振幅均比双向流固耦合大。

(2)管道内流体速度分布较不规则，在管道的CD段出现了垂直于管道向外的速度，管道的弯曲处会出现紊流现象；管道内部压力分布较为均匀，但是在CD 段出现了局部压力较大的区域，流体压力与管道壁面之间发生了强烈的泊松耦合效应，导致流体对CD端的管壁作用力变大。

(3)流体压强对管道的固有频率的影响比流体速度的影响大，在一定的压强范围内，管道的固有频率随着流体的压强增加而增加，因此在管道设计的过程中，要充分考虑压强对管道的影响。此外，管道总变形量和等效应力也是随流体压强和支管流速增加而增加的。