安时积分和扩展卡尔曼滤波的荷电状态估算

杨伟东　董浩　万峰

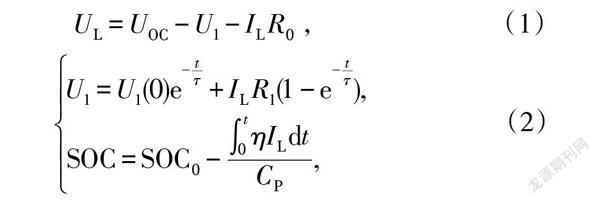
文章编号：1007-2373（2022）01-0015-06

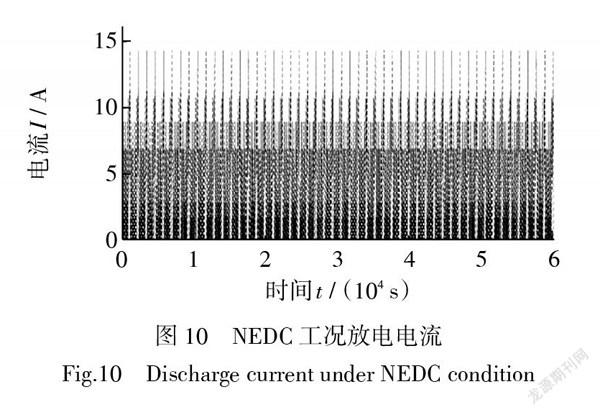
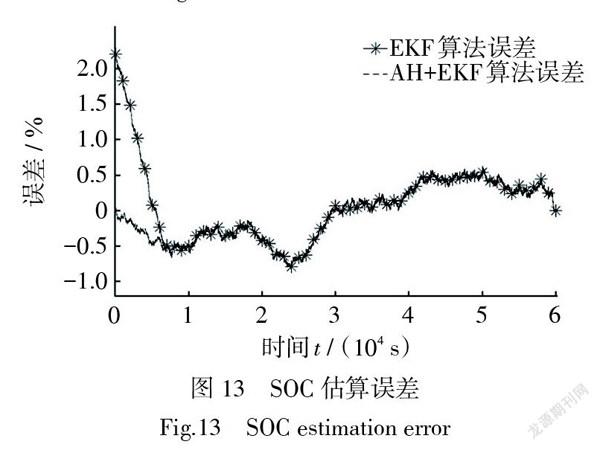
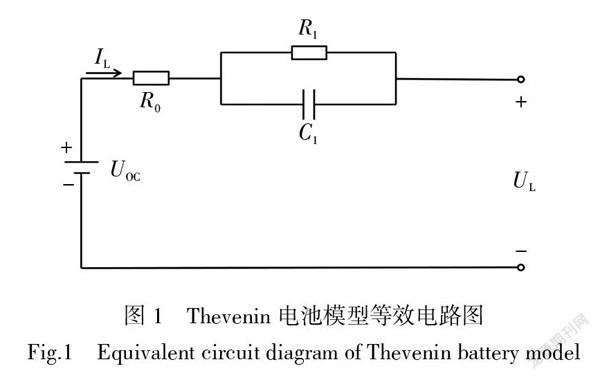
摘要 电池在满电状态无法进行混合动力脉冲能力特性测试（Hybrid PulsePower Characteristic，HPPC），导致电池参数在荷电状态（State of Charge，SOC）值为0.9～1区间无法辨识。针对这一问题，提出了安时积分（Ampere Hour， AH）与扩展卡尔曼滤波（Extended Kalman Filter，EKF）综合估算SOC的方案。首先基于HPPC实验数据对建立的Thevenin模型进行参数辨识，然后使用新欧洲行驶工况（New European Driving Cycle，NEDC）对AH+EKF综合估算方案进行了验证。验证结果表明采用AH+EKF综合估算方案大大降低了EKF法在SOC值为0.9～1区间的估算误差，当只采用EKF法的最大误差为2.2%，而使用AH+EKF综合估算方法最大误差不超过0.9%。该方法提高了SOC估算精度，取得了较为理想的效果。

关 键 词 锂电池;荷电状态;安时积分;扩展卡尔曼滤波;HPPC实验

中图分类号 TM911     文献标志码 A

Estimation of state of charge based on Ampere Hour

integration and extended Kalman filter

YANG Weidong1，2， DONG Hao1， WAN Feng1

（1. School of Mechanical Engineering， Hebei University of Technology， Tianjin， 300401， China; 2. National Engineering Research Center for Technological Innovation Method and Tool， Tianjin， 300401， China）

Abstract When the battery is fully charged， the hybrid pulse power characteristic （HPPC） cannot be tested resulting in that the battery parameters cannot be identified in the state of charge （SOC） range of 0.9～1.0. In order to solve the problem， an integrated SOC estimation scheme based on Ampere Hour （AH） and extended Kalman filter （EKF） is proposed. Firstly， the parameters of Thevenin model are identified based on the experimental data of HPPC， and then the comprehensive estimation scheme of AH + EKF is verified by using the new European driving cycle （NEDC）.The verification results show that the AH+EKF comprehensive estimation method greatly reduces the estimation error of EKF method in the SOC value range of 0.9～1.0. The maximum error of EKF method is 2.2%， while the maximum error of AH+EKF comprehensive estimation scheme is less than 0.9%. This method improves the estimation accuracy of SOC and obtains good results.

Key words lithium battery; state of charge; Ampere Hour; extended kalman filter; hybrid pulsepower characteristic

当前存在的智能优化算法，均带有各自的优点，但同时又各自存在或多或少的缺点。如：传统遗传算法虽然全局寻优能力较好，但是局部寻优能力较差，且容易陷入局部最优，容易早熟。粒子群算法的局部寻优能力较优，但是全局优化能力较差，还有一些其他的算法有各种不同的缺陷。为了弥补某些优化算法的缺陷，两种或者两种以上的优化算法的有效结合的理念便被大多数学者采用。针对粒子群算法在处理多峰函数优化问题时容易陷入局部寻优的问题，收敛速度慢等问题，Zhang等[1]将粒子群算法与正交学习法相结合，来提高粒子群算法的收敛速度。针对遗传算法在处理复杂多峰函数优化问题时易于早熟和局部搜索能力差的等问题，大量的工作者针对该问题做了许多工作。主要工作集中在两方面，一方面是提高遗传算法的局部寻优能力，另一方面主要是降低遗传算法的陷入早熟的可能性，保持遗传算法在进化过程中的种群的多样性。提高遗传算法的局部寻优能力主要是将具有较强局部寻优能力优化算法，例如粒子群算法，与遗传算法结合来提高遗传算法的局部寻优能力[2-3]。保持种群多样性的工作主要是将小生境技术，或者其他技术引入到遗传算法中，来维持种群的进化过程中的多样性，降低算法陷入早熟的可能性[4]。然而，传统小生境遗传算法虽然在种群多样性上保持的较好，但是其局部搜索能力有待提高[5]。而且小生境遗传算法对于不同问题的小生境半径的确定都需要在开始之前经过大量的测试，以此来得到一个较为准确的参数设置。工作者们对此提出的解决方案，如动态调整小生境半径[6-8]。为了解决小生境遗传算法存在的早期成熟和陷入局部极值点等问题，部分学者对于此的改进主要集中在小生境遗传算法的交叉概率和变异概率的动态调整上[9-12]。但是经过实际测试发现：‘S’型曲线的动态调整方式在进化代数较大的时候，會出现交叉概率和变异概率在短暂几代中的突变。这有悖动态调整的最初设想。为此本文对于动态调整的公式做了进一步的改进。同时，这里调整了排挤小生境的操作方式，将小生境中的所有个体施加了一个等级削减。这样可以既保留了个体之前所具有的适应度优势，同时又给同一小生境中的适应度较低的个体进行了适应度的削减。完成了小生境的排挤操作。

数十年来，对于橡胶材料的研究已经有了十足的发展。对于橡胶材料的特性的认识已经较为全面。橡胶材料在实际应用中主要表现出一种非线性弹性特性，可作为超弹性材料处理。 当前工作者对于描述橡胶的本构模型主要集中在多项式模型和Ogden模型。这些本构模型的材料参数都必须从橡胶实验中得出。但是通过材料实验确定材料参数的方法相对繁琐，同时试件之间的尺寸差异和试件的制作工艺都会对实验有或多或少的影响[14]。于是参数反演的求参方式便被多数学者采用来获取橡胶的材料参数[15-19]。 Bohdana[15]采用非线性优化方法对于填充橡胶的粘弹性本构模型进行了参数识别，并采用粘弹性本构模型以及识别得到的材料参数对于碳黑填充橡胶的松弛，压痕以及圆柱压缩进行了数值计算。为了研究橡胶的力学属性，Guelon等[16]提出了一种用于橡胶材料参数识别的反演方法。Hartmann[17]基于不可压缩材料的Rivlin’s 超弹性本构关系，对碳黑填充橡胶进行了参数识别的工作。Wen等[18]提出了一种高精度的非线性动力学模型和参数识别方法，用于预测冲击试验中橡胶波形发生器产生的冲击脉冲。杨坤鹏等[19]利用等效阻尼理论对金属橡胶隔振系统进行了动力学建模，然后利用遗传算法对其进行了参数识别工作。

本文选取了多项式模型作为拟合硫化橡胶的单轴拉伸实验。然后将本文所提出的改进型遗传算法作为参数反求的搜索算法，并将该参数反求程序应用到计算橡胶材料的材料参数上去。

1 小生境遗传算法的改进

1.1 交叉概率和变异概率的动态调整

进化算法的种群在一开始一般是随机生成的，种群的多样性较强。种群进化的方向应该是向着收敛方向前进。在进化初期，变异操作未起主要作用，为最大范围搜索到所需要的极值，可使交叉概率比较大，随着进化次数的增加，种群逐渐趋向于极值，种群已经基本上趋于稳定，为了跳出局部最优解，保持种群多样性，应该降低交叉概率，增大变异概率，从而加速算法的收敛过程。武兴亮等[9]对于动态交叉概率和变异概率采用了如下的调整公式：

式中：[Pcro]为初始交叉概率;[Pmut]为变异概率;[GEN]为总的遗传代数;[x]为当前的进化代数。对此函数进行一次测试（这里以遗传代数10，30，100代为例，初始交叉概率为1，变异概率为0.2），其动态调整的变化如图1所示。通过对比图1中的a），b），c），会发现武等[9]所提出的用于小生境交叉和变异概率的动态调整公式会在进化中期代会有一个突变，无法实现在进化的整个过程中对该两个概率有一个很好的过渡调整。

对于小生境交叉概率和变异概率的动态调整策略， 为了使其在整个变化过程中有一个很好的过渡，本文提出了改进的动态调整公式。如式（3），式（4）所示：

式中：[Pcro]是初始交叉概率;[Pmut]是初始变异概率;[TMAX]是总的遗传代数;[gen]是当前遗传到的代数。通过对比图2中的a），b），c），会发现本文所提出的动态调整公式会使得交叉概率和变异概率在整个进化过程中有一个很好的动态平稳过渡，提升了算法的性能。

这样也基本满足了对于交叉概率和变异概率的动态调整的要求。在进化初期，种群分散度较大，应该把交叉概率调大，变异概率调小。在进化后期，个体之间逐渐趋于同一小生境内，或者趋于同一极值点，调大变异概率来让种群跳出局部最值点。在进化中期时，本文所提出的变异交叉概率将会平稳的过渡。 此动态调整公式被选取作为本次的改进型小生境遗传算法的交叉概率和变异概率的动态调整公式。

1.2 小生境的排挤和衰减因子

对于处于同一个小生境内的个体，要对适应度低的个体在适应度上施加一个罚因子。文献[9]对于同一小生境内的适应度较低的个体的处理是将该个体的适应度归0。但是在多维问题中，即使适应度较低的个体，也可能保留着非常优秀的信息[13]。如果直接将该个体的适应度归0，可能对于提高算法的收敛速度并不会起促进作用。本文对此提出的改进意见如下所示。

1）首先找到在同一小生境内的所有个体。

2）然后按照适应度降序的顺序将个体进行排序。将这些个体写入到一个列表，记名为：[Ik]，[k=1，2，3…] 。

3）对[Ik]中的第[k]个个体在适应度上施加一个削减因子[1k]，[k=1，2，3…] 。

该改进的小生境排挤操作具有如下的性质。

1）在对于同一小生境内的个体，本文抛弃了对于那些适应度较低的个体进行了适应度归0的操作，然后对于不同适应度的个体会施加一个不同的削减因子。

2）既不希望將适应度低的个体的适应度削减太多，又不会给同一个小生境内的所有的个体都进行相同的削减，因为不同个体的适应度值并不一定相同，不应该对于不同适应度值的个体进行相同的削减。这样个体才会因为自己本身的适应度优势做出不同的调整策略。于是本文做出的改进便如上所示。

1.3 改进小生境遗传算法的具体实现步骤

步骤1：初始化种群[Qg]，初始种群规模为[N]，初始演化代数[g=1]。

步骤2：计算出种群的适应度列表[Fg]。

步骤3：依据[Qg]每个个体的适应度对其进行降序排列，并记忆前[M]个个体，不妨取[M=N2rand+1]， 其中[rand]为[0∼1]之间的随机数。

步骤4：对随机生成的[N]个个体采用比例选择运算，得到群体[Q'g]。

步骤5：交叉和变异。初始交叉概率[Pcro]，变异概率[Pmut]，并对群体[Q∗（g）]利用式（3）和式（4）来调整交叉和变异概率，得到群体[Q″（g）]。

步骤6：将步骤 4得到的[N]个个体和步骤 3记忆的[M]个个体的新群体[Hg]。

然后对[Hg]按照适应度降序的顺序对种群进行排序。进入步骤6.1。

步骤6.1：挑选出当前列表[Hg]中适应度最大的个体作为小生境的中心[xc]。并将该个体从[Hg]中去掉。然后在[Hg]中挑选出那些相对于小生境中心的距离小于指定的小生境半径的所有个体。即为当前小生境内的所有个体。然后将这些被选中的个体从[Hg]中排除掉。进入步骤6.2。

步骤6.2：将剩下的个体重新按照适应度降序排列，重复步骤6.1。直到[Hg]中的所有个体被选择完毕。

步骤6.3：对经过步骤6.2所生成的所有列表进行小生境操作。对各列表中所有个体进行等级削弱。

步骤7：经过步骤6～步骤 6.3处理之后的列表重新归并到一起，记名为[Lg]。然后按照适应度降序排序。

步骤8：终止条件的判断。若满足终止条件，则输出算法结果，算法完成，若不满足终止條件，进入步骤9。

步骤9：保留[Lg]中前[N]个个体，更新演化代数[g]。

2 改进小生境遗传算法在橡胶参数反求上的应用

2.1 材料参数反求的主要思想

首先假定材料参数，采用有限元进行正向分析，计算出一个仿真响应。然后将仿真响应与实验响应进行对比。通过优化算法不断调整材料参数，直到找到一组材料参数使得仿真响应与实验响应之间的误差最小[20-21]。

本文便选用改进的小生境遗传算法作为优化搜索算法，来实现对于橡胶的材料参数反求。

2.2 对于橡胶材料的单轴拉伸实验

对于单轴拉伸试验，本文参考最新的国家标准GB_T 528-2009《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》，选用标准所规定的1型哑铃状试件，厚度为2 mm。根据国家标准，试件的实验部分为中心的25 mm，即认为在这部分范围内产生最大均匀变形，用两个黑色的标定线标定。实验设置如图3所示。采用Instron3365万能材料实验机完成单轴拉伸实验，该试验机载荷量程为5 kN，载荷由实验机内置传感器测得，并根据试件的横截面积得到名义应力;位移由接触式引伸计测得，并由此得到名义应变。在进行单轴拉伸实验时，首先设置实验参数，包括试件的形状尺寸、拉伸方法等等。接着用夹具夹紧哑铃状试件的上端;然后调整位置，确保上下端是垂直方向，并且夹具所夹的部分大小一致，保证实验部分，即两黑色标定线之间部分，在测试范围内。接着调整实验机，使之达到稳定状态，用接触式引伸计夹在两条标定线的位置。完成上述操作后，开始进行实验和采集数据，为了消除MULLINS效应，即在预应力作用后表现的应力软化现象，每个试件在正式拉伸前均进行预循环实验，如果试件在预循环拉伸过程中断裂，或者断裂位置在标定线范围之外，需要将这组实验数据舍去，重新进行下一个试件的实验。

图4是5个试件在多次拉伸后曲线趋于稳定的名义应力和应变曲线。

由图4中曲线可以看出，不同试件的应力应变曲线差异性较小，说明实验结果较为集中，因此可以认为实验是成功的，这些数据结果是有效的。为了减小实验中的一些误差对结果的影响，应该选用平均值曲线的数据进行参数反求。

2.3 橡胶超弹性材料本构模型理论

图5是本文的单轴拉伸的有限元模型。在连续介质力学中，认为橡胶是各向同性材料，用单位体积的应变能来表示本构模型。它对应变分量的导数就是相应的应力分量。应变能可以分解成应变偏量能和体积应变能两部分，其多项式形式如下：

式中：n是多项式的阶数;[Cij]和[Di]是温度相关的材料参数;[I1，I2]是和主伸长率有关的第1第2主不变量。[J]是弹性体积比，[J=1]时可以认为材料是不可压缩材料。

本文选取当[n=2]时的多项式本构模型进行材料参数的反求。

2.4 参数反求及其结果

为了与通过参数反求工作所计算出来的结果进行一个对比，首先通过ABAQUS材料属性模块中的Evaluate功能来得到材料参数，如表1所示。

通过该材料参数计算出来的仿真响应与实验响应的对比图如图6所示。

观察图6，可以发现通过Evaluate计算得到的仿真响应与实验响应从应变一开始便有很大的偏差。而且随着应变的递增，实验响应与仿真响应之间的偏差会越来越大。除本构模型对于该橡胶材料的大变形阶段的描述不准确之外，其材料参数也是与实际值更有一个较大的偏差。因为采用该本构模型在应变低于1.5时，实验响应与仿真响应之间的误差同样较大。

接下来便通过反演程序来计算该橡胶材料参数，参数反演的主要思想如Section 2.1所述，通过Python编写了该反演程序，其中改进小生境遗传算法主要是用来在指定参数范围内找到较为优秀的材料参数值，该参数值能使得实验响应与仿真响应之间的误差最小。对于该反演程序所需要的各参数范围定义如表2所示。

参数反演计算得到的橡胶材料参数如表3所示。

通过表3所示的材料参数所计算出来的仿真响应与实验响应的对比图如图7所示。

通过对比图6和图7，可以发现，图7所示的实验响应和仿真响应之间的偏差要远小于图6所示的两者之间的偏差。所得到的材料参数相对于ABAQUS的参数拟合所得的材料参数要更加接近实际值。说明通过本文所提出的参数反演技术来计算得到的材料参数更加精确。但是我们也注意到在应变超过150%之后，实验响应与仿真响应之间的偏差开始逐渐增大，除了实验精度的误差之外，本文的结果也表明2阶多项式模型无法准确描述硫化橡胶的大变形阶段的应力/应变响应。如果通过2阶多项式模型来预测硫化橡胶的大变形，其预测得到的橡胶所产生的应力会远远大于实际橡胶的单轴拉伸实验所产生的拉伸应力。

3 结论

1）本文对于小生境遗传算法的改进，使得遗传的交叉概率和变异概率在整个变化的过程中都处于动态调整，且在整个进化过程中，交叉概率和变异概率不会在某几代中发生突变。使得动态调整贯穿整个进化过程。这样的改进可以有效维持小生境遗传在进化过程中的种群多样性。而且我们对于小生境的排挤操作的改进能充分利用每一代中的每个个体的优秀信息，加快算法的收敛速度。

2）通过有限的实验来获取材料参数，参数反求是一个非常优秀且广泛使用的方法。本文对于橡胶材料的参数反求结果显示我们的方法能获取到一个与实际参数值比较接近的结果。采用本文所获取到的材料参数能更好的预测橡胶的变形特性。

参考文献：

[1]    ZHAN Z H，ZHANG J，LI Y，et al. Orthogonal learning particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation，2011，15（6）：832-847.

[2]    JUANG C F. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part B （Cybernetics），2004，34（2）：997-1006.

[3]    JUANG C F，LIOU Y C. On the hybrid of genetic algorithm and particle swarm optimization for evolving recurrent neural network[C]//2004 IEEE International Joint Conference on Neural Networks （IEEE Cat. No. 04CH37541），Budapest，Hungary. IEEE，2004：2285-2289.

[4]    WEI L Y，ZHAO M. A niche hybrid genetic algorithm for global optimization of continuous multimodal functions[J]. Applied Mathematics and Computation，2005，160（3）：649-661.

[5]    黃聪明，陈湘秀. 小生境遗传算法的改进[J]. 北京理工大学学报，2004，24（8）：675-678.

[6]    喻寿益，郭观七. 一种改善遗传算法全局搜索性能的小生境技术[J]. 信息与控制，2001，30（6）：526-530，542.

[7]    陆青，梁昌勇，杨善林，等. 面向多模态函数优化的自适应小生境遗传算法[J]. 模式识别与人工智能，2009，22（1）：91-100.

[8]    LIN C Y，WU W H. Niche identification techniques in multimodal genetic search with sharing scheme[J]. Advances in Engineering Software，2002，33（11/12）：779-791.

[9]    武兴亮，丁根宏. 改进小生境遗传算法求解多峰函数优化问题[J]. 信息技术，2013，37（1）：73-76.

[10]  乔佩利，郑林，马丽丽. 一种小生境遗传算法研究[J]. 哈尔滨理工大学学报，2011，16（1）：90-93.

[11]  赵敏，林道荣，瞿波，等. 一种新的基于小生境模拟退火的遗传算法[J]. 辽宁工程技术大学学报（自然科学版），2013，32（3）：367-372.

[12]  王聪，柯沪琦，胡燕海. 改进的小生境混合遗传算法在函数优化上的应用[J]. 传感器与微系统，2017，36（5）：153-156.

[13]  MENDES R，KENNEDY J，NEVES J. The fully informed particle swarm：simpler，maybe better[J]. IEEE Transactions on Evolutionary Computation，2004，8（3）：204-210.

[14]  张军，成艾国，宋凯，等. 基于移动最小二乘响应面法的橡胶材料参数反求[J]. 汽车工程，2011，33（3）：271-275.

[15]  MARVALOVA B. Identification of viscoelastic model of filled rubber and numerical simulation of its time dependent response[C]//İNAN Esin，SENGUPTA Dipak，BANERJEE Muralimohan，et al. Vibration Problems ICOVP-2007，Springer，2008：273-279 .

[16]  GUÉLON T，TOUSSAINT E，LE CAM J B，et al. A new characterisation method for rubber[J]. Polymer Testing，2009，28（7）：715-723.

[17]  HARTMANN S. Numerical studies on the identification of the material parameters of Rivlin's hyperelasticity using tension-torsion tests[J]. Acta Mechanica，2001，148（1/2/3/4）：129-155.

[18]  WEN J J，LIU C W，YAO H P，et al. A nonlinear dynamic model and parameters identification method for predicting the shock pulse of rubber waveform generator[J]. International Journal of Impact Engineering，2018，120：1-15.

[19]  杨坤鹏，樊文欣，曹存存，等. 金属橡胶材料的动态力学建模及参数辨识[J]. 机械科学与技术，2017，36（12）：1830-1833.

[20]  FREUTEL M，GALBUSERA F，IGNATIUS A，et al. Material properties of individual menisci and their attachments obtained through inverse FE-analysis[J]. Journal of Biomechanics，2015，48（8）：1343-1349.

[21]  BÖL M，KRUSE R，EHRET A E，et al. Compressive properties of passive skeletal muscle—The impact of precise sample geometry on parameter identification in inverse finite element analysis[J]. Journal of Biomechanics，2012，45（15）：2673-2679.

收稿日期：2020-12-05

基金项目：河北省教育厅重点研发项目（ZD2017215）

第一作者：杨伟东（1972—），男，教授。通信作者：万峰（1971—），男，教授，wf_hebut@163.com。