基于试飞数据的扭矩电桥筛选方法研究
2022-03-07陈致名CHENZhiming
陈致名 CHEN Zhi-ming
(中国飞行试验研究院,西安 710089)
0 引言
根据国军标及相关适航条例,飞行载荷测量试验是验证飞机结构设计、完成新机定型必须完成的试验项目。飞行载荷的测量方法目前可分为直接方法和间接方法。应变法和压力分布测量方法可直接获得机翼上某假定剖面的载荷或飞行载荷沿机翼的分布,被称为直接方法;风洞法和参数辨识法被称为间接方法,风洞法借助地面风洞试验数据预测飞行中某状态点的飞机受载,参数辨识法结合虚拟实验方法建立模型,通过飞行参数间接算得飞行载荷[1-2]。目前,应变法凭借实施方法简单、数据处理高效、结果可靠性高等特点,广泛用于飞行载荷测量[3-4]。应变法利用在蒙皮、梁腹板及上下缘条等结构所改装的应变片,通过地面载荷校准试验建立结构载荷与应变之间的关系,在飞行数据处理过程中,结合应变数据及相关飞行参数,可以计算飞机各剖面结构载荷,并估算出气动载荷。
目前在对飞机结构进行预先应变改装后,可通过改装的惠斯通电桥得到对应改装位置的应变值,通过地面载荷校准试验,可以建立应变与载荷的关系。飞行载荷测量所需要计算的载荷类型为剪力、弯矩及扭矩,通过地面试验建立各载荷对应载荷方程后,可以计算得到相应载荷。载荷方程的形式为选用的带有系数的惠斯通电桥的线性叠加,具体电桥选用规则为:在保证电桥主要感受载荷为对应方程的载荷的前提下,实现载荷解耦,保证其余类型载荷所引起惠斯通电桥产生响应后,该载荷方程输出值产生尽量小的变化。因此扭矩方程里选用电桥通常为扭矩电桥,根据结构情况偶尔选用弯矩电桥、剪力电桥。受飞机翼面形状受限,相比于剪力及弯矩,扭矩的数值基本较小,误差较大,扭矩方程计算结果误差也大于剪力方程及弯矩方程,因此在建立扭矩方程过程中,对响应扭矩电桥的选择需要慎重考虑。
应变法中对扭矩电桥的筛选依据是地面载荷校准试验中电桥所表现出的数学特性。如需在地面试验时实现载荷解耦,需设计各个剖面的纯扭矩工况,保证剖面只受扭矩而不受剪力、弯矩及拉压,工况设计复杂、施加难度大且易产生误差,且对于复杂结构飞机无法应用纯扭转工况。由电桥筛选方法所限,对扭矩电桥的筛选结果精度有限且结果并不直观,仍需在试飞过程中建立多个扭矩方程,判断各方程的精度并最终筛选出扭矩电桥[5-7]。
本文利用电桥的物理特性,在起飞阶段依据飞行参数将弯矩、剪力与扭矩对扭矩电桥的影响进行解耦,通过量化指标的方法,对扭矩方程中选用的扭矩电桥进行筛选。
1 基本原理
1.1 载荷方程原理
建立各载荷方程的基础是地面载荷校准试验。通常外载荷与应变计输出信号之间的关系可以认为是线性的,但是加载时结构会受到拉压力、剪力、弯矩和扭矩的综合影响,不同的外载荷可能会使某个电桥产生同样的信号输出,可以通过不同应变计电桥的惠斯通电桥形式及载荷校准试验所建立的载荷方程可以将载荷进行解耦,由于复杂结构中结构载荷的传力路径难以准确分析,需要将剖面上不同位置的电桥所感受到的力的特性综合分析计算剖面的结构受载情况,载荷方程的广义形式如式(1):
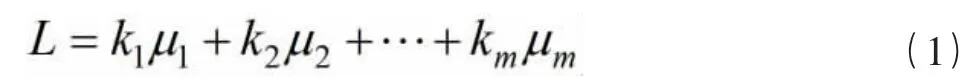
上式中L是结构载荷,ki是载荷方程中电桥对应的拟合系数,μi是电桥i的输出。式(1)中拟合系数可视为各电桥输出对于结构载荷值的权重系数,拟合系数较大的电桥对结构载荷产生较大影响,该式中默认偏置值为0,即未施加外载荷时,电桥输出皆为0,符合物理猜想结构无外力影响时不产生变形。
理想的载荷方程应符合以下关系:
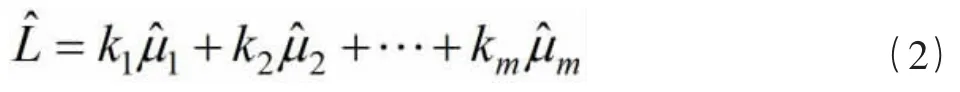
式(2)中,L^是飞机在飞行中实际受到的外载荷,μ^i是电桥i的输出。式(2)中拟合系数与式(1)中拟合系数相同,利用载荷校准试验建立的载荷方程即各电桥对应拟合系数与飞行中电桥输出可以计算飞行实测载荷。
1.2 扭矩电桥工作原理
应变法将每个剖面的飞行载荷分为弯矩、剪力及扭矩,首先在飞行器部装或总装阶段对待测结构剖面处进行应变改装,在各载荷敏感结构处布置应变片并组成全桥形式惠斯通电桥或半桥形式惠斯通电桥,将安装好的电桥与测试设备进行连接。各剖面具有多个对不同形式载荷分别敏感的不同电桥,各载荷方程除了选用对该类型载荷敏感的惠斯通电桥外,还应选用其余电桥参与载荷方程的建立,基于地面载荷校准试验所建立的载荷方程,选用各剖面不同电桥计算各剖面载荷。在地面载荷校准试验前,为了将弯矩、剪力及扭矩解耦,需分析各种受载情况下飞机各部件结构的受载形式,比较各部件结构对不同形式载荷的敏感程度,在最敏感的结构处布置相对应的电桥。以双梁结构为例,由于结构较简单,将剪力电桥布置在前梁、后梁的腹板位置,将弯矩电桥布置在上下缘条位置,将扭矩电桥布置在蒙皮上[8-9]。
将扭矩电桥布置在蒙皮上的原因是蒙皮构成的翼盒结构承担主要扭矩,且扭矩引起的剪流在蒙皮上传递。应变法中测载电桥均选用惠斯通全桥,基于剪流的物理特性,扭矩电桥安装位置通常布置在剖面处蒙皮外侧,弦向位置远离前缘及后缘即可,扭矩电桥位置及其感受应力形式如图1所示。

图1 扭矩电桥位置及其感受力
由图1可知,对于惠斯通电桥,扭矩引起的剪流会导致图中所布置电桥产生电桥输出,但是同时,剪力、弯矩等其余类型的载荷也会引起该电桥产生输出,因此处理载荷校准试验数据时需要在扭矩方程中引入其余电桥降低剪力、弯矩等其余类型的载荷对扭矩方程引起的误差,降低误差的方法需要利用载荷校准试验数据,加载工况的合理设计与试验数据的有效处理可以有效降低方程误差。
不同扭矩电桥的粘贴位置、粘贴方向、与结构的连接度不同都会影响扭矩电桥在载荷校准试验与飞行实测中的效果,各因素会导致其分别对剪流、正应力的敏感程度不同。在各载荷方程中,应优先选择对该类型载荷较为敏感的电桥以降低方程误差,再基于载荷校准试验数据中多电桥对加载载荷的响应采用数学-物理方法实现载荷解耦。
2 扭矩电桥筛选原理
飞机操纵面、翼面等结构所受扭矩大小由气动载荷大小与气动压心至转轴、刚轴之间的距离共同确定,飞机飞行中翼面所受气动载荷的计算公式与翼面结构所受扭矩载荷的计算公式如式(3)~式(4)所示。

由式(3)~式(4)可知,当飞机结构未产生较大变化、气流密度未产生较大变化时,翼面所受剪力大小主要和飞机空速及升力系数有关。而由机动动作中压心变化规律计算结果可知,压心分布与气流流场在翼面的分布形式有关,当飞机飞行速度处于亚音速时,流场的分布形式和飞机姿态角及姿态角速率等参数有关,当飞机进行机动动作,压心位置主要和飞机姿态角及姿态角速率有关,当飞机做纵向机动时,压心的弦向位置与迎角基本成正比例关系。
基于以上分析观察某大型客机起飞过程中右侧机翼某剖面扭矩电桥T3、同一剖面扭矩电桥T4的输出及飞机飞行参数:地速、迎角、气压高度等的变化,如图2所示。(图中数据已经过脱密处理,横坐标为时间历程,未标出具体时间,数据及飞行参数单位已隐去)
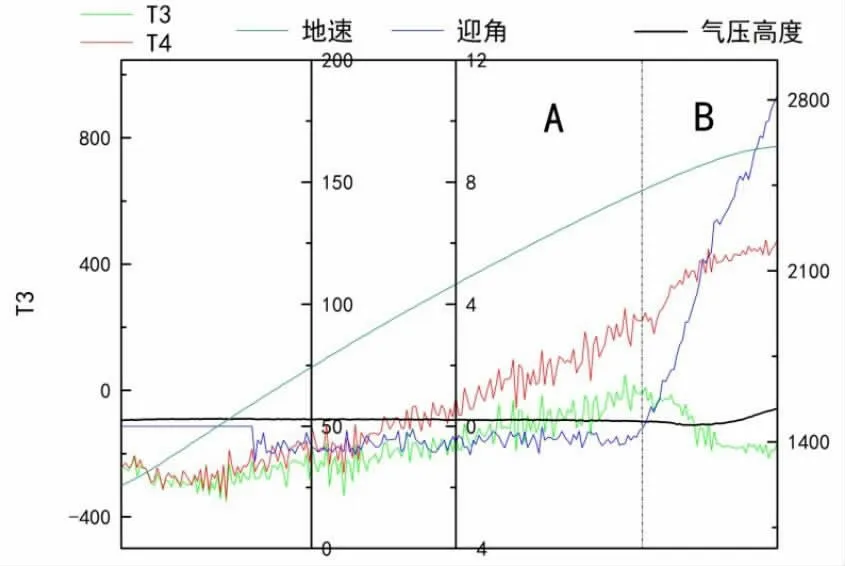
图2起飞过程中电桥响应及飞行参数随时间历程变化
图2 左侧为A区,右侧为B区,A区中发动机开车,飞机开始地面滑跑速度逐渐增加,但迎角始终接近于零,由于迎角接近零时压心接近刚轴,扭力臂较小,剪流始终较小,因此该过程中正应力绝对值变化较大,剪流绝对值变化较小;B区中随着速度增加,升力达到一定值后,飞机抬头开始爬升,迎角迅速增加,由于该过程中飞机速度变化不大,升力系数随迎角增加而增加,压心位置随姿态角及姿态角速率的变化而大幅变化,因此该过程中正应力变化值相比于剪流较小,B区内电桥输出可视为主要受扭矩影响。由上述分析可知,对于扭矩电桥,A区为正应力影响区,B区为剪流影响区。
基于上述分析,定义某类型单位载荷引起的电桥数出为该电桥对该型载荷的敏感因子,对不同类型载荷敏感因子之比为敏感因子比。式(5)~式(7)中给出扭矩电桥对正应力、剪流敏感因子及敏感因子比公式的定义。
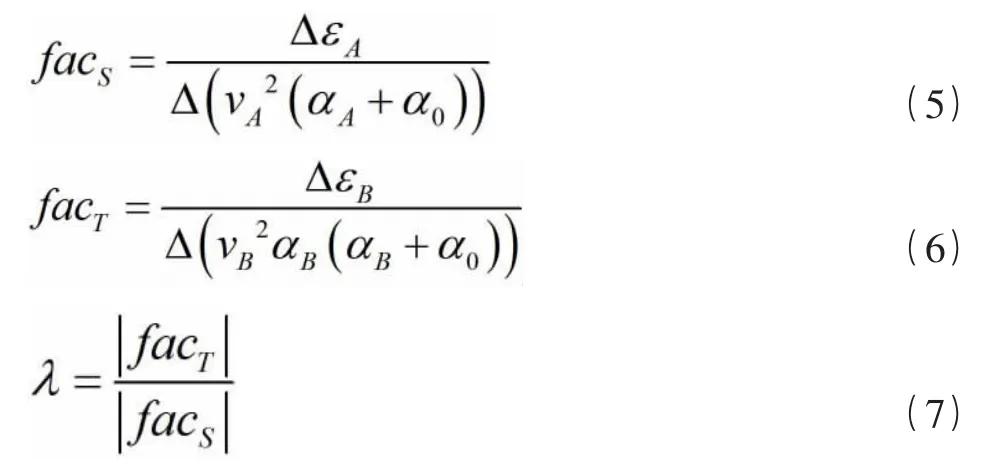
式中α0为零升迎角,分别依据A区与B区的速度、迎角、电桥输出等变化量对该电桥的敏感因子及敏感因子比进行计算,敏感因子比λ越大,代表该扭矩电桥更适合用于扭矩方程。
3 筛选结果及试飞验证
整理该型机三个架次的起飞过程中的试飞数据,并计算该剖面扭矩电桥T3、T4在三个架次中分别对正应力、剪流的敏感因子及敏感因子比,计算结果如表1所示。
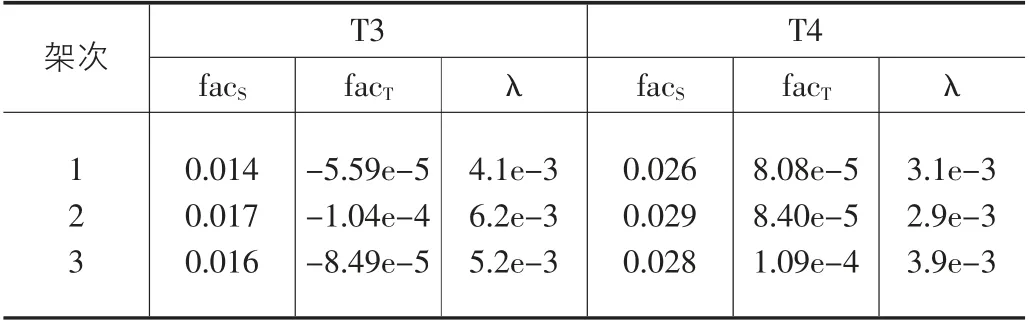
表1 三架次中正应力及剪流的敏感因子(比)
由表中总结数据可知,三个架次中,T3电桥的敏感因子比均大于T4电桥的敏感因子比,依据理论推导,T3电桥对剪流更加敏感。分别尝试将T3电桥或T4电桥建立扭矩方程,两扭矩方程构成如表2所示。
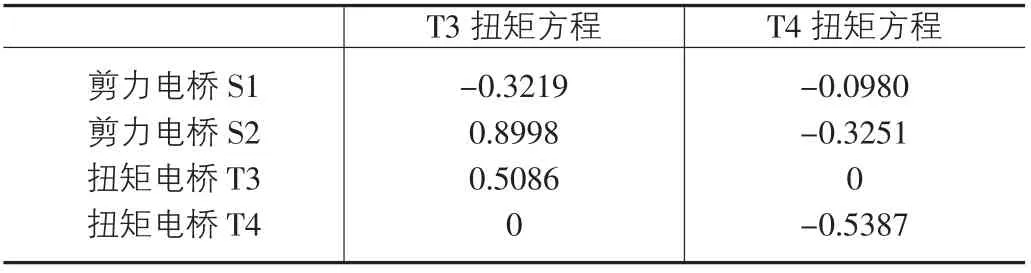
表2 采用T3及T4电桥的扭矩方程
分别利用两扭矩方程计算架次1中飞机起飞后爬高度过程中该剖面扭矩变化,扭矩方向定义为使飞机抬头为正向,对比结果如图3所示。
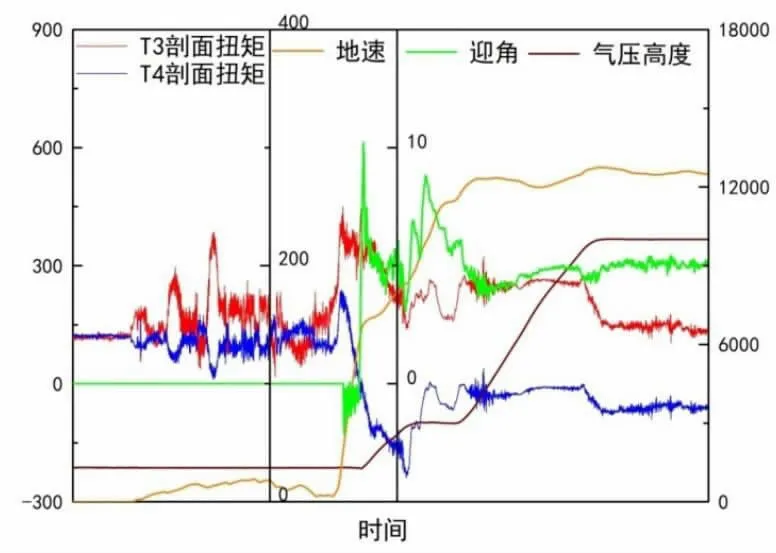
图3起飞过程中两扭矩方程计算所得扭矩
图3 中数据包含飞机从地面发动机开车、加速滑跑、飞机拉起爬升到平飞四个过程,从图中数据可以看出,两扭矩方程计算结果之间的扭矩差较大,扭矩差主要出现在飞机加速滑跑至拉起爬升初始阶段,且该过程中迎角始终接近于零,而飞机速度迅速增加,当飞机速度逐渐稳定时,扭矩差趋于稳定。
由风洞试验数据可知,通常当迎角增加时,机翼前缘受载增加,压力中心前移,而由于扭矩方向定义为使飞机抬头为正向,在速度未降低的条件下,飞机大迎角爬升阶段扭矩值应增加,T4剖面扭矩计算结果显然与理论分析不合,T3剖面扭矩变化趋势与理论分析相符。
将飞机起飞爬高度过程中采用T3电桥计算所得剖面扭矩与左侧对称剖面扭矩值进行对比,结果如图4所示。
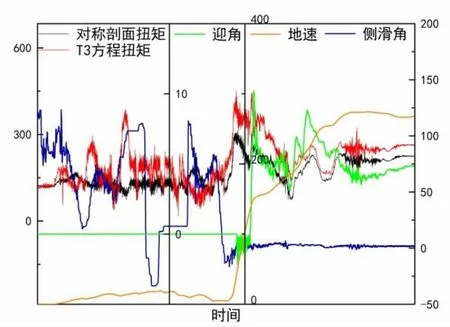
图4 起飞过程中左右扭矩方程对比结果
由图4中数据可知,起飞滑跑阶段飞机为大侧滑角状态,左右对称剖面扭矩不一致,当飞机开始爬升后侧滑角逐渐接近于0,左右对称剖面扭矩之差减小,最后趋于一致。
由以上同侧两方程计算扭矩对比及对侧扭矩对比结果可知,选用敏感因子比更高的T3电桥所建的扭矩方程计算所得载荷规律与预期更相符,且左右对称性效果更好。
4 结论
①对于布置位置接近,物理特性有差异的扭矩电桥,采用本文方法可有效识别其对扭矩敏感度;②由于地面载荷校准试验中工况设计时剖面受载很难完全解耦,因此选择电桥时选用对相应载荷更敏感的电桥可有效提升载荷方程精度;③飞行中迎角与速度变化耦合,利用飞机起飞阶段数据,可有效分离正应力和剪流对扭矩电桥的影响。
