随钻压力波在用于早期气侵检测时的扰动传播特性研究*

李 鑫，张 杰，唐 旭，李翠楠，赵在鹏，刘 旭

(1.西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.西南石油大学 石油与天然气工程学院，四川 成都 610500；3.中国石油川庆钻探工程有限公司 川西钻探公司，四川 成都 610051；4.中国石油西南油气田分公司 工程技术研究院，四川 广汉 618300)

0 引言

随着油气勘探开发的整体趋势逐渐向深层及超深层扩展，钻井作业的深度也随之不断加深，地层的情况越发复杂，发生危险工况的概率也逐渐增大。在钻井作业的过程中，如果井筒内的压力不能有效地平衡地层孔隙压力，则会导致地层流体(油、气、水)持续不断地侵入井内，从而引发溢流。若溢流的检测与控制不及时，其会进一步演化为井涌，严重时甚至会引发井喷或井喷失控事故。

相比于地下原油和地层水的侵入问题，气侵引发钻井安全事故的可能性更大，且带来的后果也更加严重。其主要原因是由于气体的密度远小于钻井液的密度，其侵入井筒后会在环空内快速滑脱上升且急速膨胀，造成事故发生的速度过快，很难及时采取相应的控制措施[1-4]。因此，对早期气侵过程进行及时检测是保障钻井作业安全性的重要环节。

现场常用的气侵检测方法主要包括泥浆池液面检测法、进出口流量差法和压力检测法。前2种方法实际上是基于气体膨胀原理[5-6]。侵入气体在环空内滑脱上升的过程中所受压力不断减小，体积不断膨胀，在地面所观察到的情况即是泥浆池的液面升高和钻井液的出口流量增大。这2种方法的弊端在于只有当气体上升到井筒中上部并产生较大的体积膨胀后，才可在地面观察到较为明显的现象。因此，使用这2种方法检测到气侵的时间严重滞后，无法可靠地保障钻井作业的安全性。压力检测法主要依靠钻井作业过程中套压和立压的变化来对气侵进行检测[7-8]。气体侵入井筒后，体积不断膨胀，造成套压升高。另一方面，气体与钻井液混合后，钻井液的密度降低，井底压力减小，造成立压降低。这种方法的弊端在于受钻井参数变化的影响，套压和立压本就处于波动变化的状态，只有当气体在井筒内的浓度达到较高程度时，套压和立压才能产生较为明显的变化。因此，使用该方法检测到气侵的时间也相对滞后。

由于深井钻井作业时井下情况复杂且多变，常需结合MWD技术对实际情况进行随钻检测。MWD技术在实际作业时会产生压力波。压力波是指流场中某一局部区域发生的微小扰动传递到其他区域的波动过程。压力波具有传播稳定和输送距离长的优点[9-10]。许多工业生产都将压力波应用到安全保障中，例如核能、交通和航空航天等。目前，压力波在油气领域的研究和应用较少。李洪涛等[11]首次建立了充气钻井随钻压力波信号的衰减模型，第1次在油气领域开展了压力波的研究。Henry等[12]和Huang等[13]分别对不同流型下的压力波传播与衰减特性进行了实验测试，为压力波应用于工业生产提供了宝贵的理论依据。

但是，要将压力波应用于早期气侵检测，仍需从以下2个方面进行进一步的探索：1)实验测试所设定的压力波传播环境较为局限，相关参数变化对压力波传播的影响分析不全面；2)实验测试时所使用的介质多为空气和水所组成的两相流，与钻井作业发生气侵时的井筒流体构成有较大的差别。基于上述问题，通过建立用于模拟压力波在进行气侵检测时的扰动传播模型，对压力波在不同条件影响下的传播与衰减特性进行分析，并与压力波用于气侵检测时的实际情况相结合，对该方法的应用效果进行评价。

1 检测原理

基于MWD压力波传播特性进行早期气侵检测的基本原理是：若在钻井作业的过程中发生气侵，环空内的流体流动会由单相流(钻井液)转变为气液两相流(地层气体和钻井液)，而钻柱内的流体流动仍保持为钻井液单相流动。MWD在传递井下信息时会产生随钻压力波信号，压力波在环空气液两相流中的传播速度会比其在钻柱单相流中的传播速度发生较为明显的降低，这1点可从Ruggles等[14]、Wang等[15]及白博峰等[16]所获得的实验结果中得到验证。因此，在发生早期气侵时，随钻压力波信号经环空和钻柱传递至井口的时间会存在1个较为明显的差值。使用随钻压力波信号对早期气侵的发生进行检测正是依据压力波在2条路径传输时所用时间的差值大小来判断是否有气侵发生，并可判断气侵发生的程度。使用随钻压力波信号进行早期气侵检测的基本原理如图1所示。

图1 随钻压力波信号检测早期气侵的原理Fig.1 Schematic diagram of early gas-kick detection using MWD pressure wave signals

2 扰动传播模型

2.1 假设条件

与实验测试所设定的特定条件相比，数学模型内的参数可根据实际需要进行任意的调试，能够更加全面地模拟出压力波在不同条件和环境下的传播与衰减规律。为了便于数学模型的建立与求解，在不影响其计算结果准确度的前提下，提出以下假设条件：

1)气-液两相间均处于热力学平衡状态；

2)气-液两相与壁面处于热力学平衡状态；

3)气-液两相间无质量交换；

4)不考虑环空内岩屑对压力波传播的影响；

5)忽略气泡运动所引起的共振效应。

2.2 控制方程组

控制方程组中的连续性方程组如式(1)所示：

(1)

控制方程组中的动量守恒方程组如式(2)所示：

(2)

式中：Aann为环空的截面积，m2；ρg，ρl分别为气体和钻井液的密度，kg/m3；αg，αl分别为气体和钻井液的体积分数，%；vg，vl分别为气体和钻井液的流速，m/s；P为井筒压力，Pa；Fgl为气液两相间的界面阻力，N/m2；θ为井斜角，rad；τgw，τlw分别为气体和钻井液与套管壁的剪切应力，N/m2；dw，ds分别为井眼和钻柱的直径，m。

2.3 辅助方程组

2.3.1 气体密度计算

在井筒气液两相流流动过程中，气体可假定为理想气体，其密度计算方程如式(3)所示：

(3)

式中：Pg为气体所受压力，Pa；Z为压缩系数；R为气体常数，8.314 J/(mol·K)；Tann,k为气侵期间的井筒流体温度，K。

2.3.2 界面阻力计算

Park等[17]指出气液两相流间的界面阻力可由虚拟质量力和拖曳力构成，如式(4)所示：

Fgl=Fgl,vm+Fgl,dg

(4)

式中：Fgl,vm为虚拟质量力，N/m2；Fgl,dg为拖曳力，N/m2。

在气液两相流中，当气体相对于液体进行加速运动时，气体会给予液体1个作用力，液体也会给予气体1个反作用力，这个力即为虚拟质量力。虚拟质量力的计算方程组如式(5)所示：

(5)

式中：cvm为虚拟质量力强度系数；cm1，cm2分别为常数系数；avm为虚拟质量力加速度，m/s2；vr为滑脱速度，m/s。

在早期气侵发生时，环空内气液两相流的流态主要为泡状流。此时，气泡的形状对拖曳力的影响较大。早期气侵过程中，拖曳力的计算方程组如式(6)所示：

(6)

式中：cdg为拖曳系数；rb为气泡的半径，m；σs为表面张力，N/m2；g为重力加速度，9.8 m/s2。

2.3.3 剪切应力计算

在泡状流中，气体均匀地分布在钻井液中，或与套管壁之间有1层液膜相隔，不会与套管壁直接接触。因此，在发生早期气侵时，侵入气体与套管壁之间的剪切力可以忽略不计。钻井液与套管壁之间的剪切应力计算方程组如式(7)所示：

(7)

式中：flw为钻井液与套管壁之间的剪切应力系数；μl为钻井液的运动黏度，m2/s。

2.3.4 传播速度计算

在等熵的条件下，压力波在气相和液相中传播速度的计算方程组如式(8)所示：

(8)

式中：vpw,g，vpw,l分别为压力波在气体和钻井液中的传播速度，m/s。

2.3.5 压力波扰动计算

压力波在气液两相流中传播时会发生扰动。当扰动发生后，气液两相流中物性参数的计算方程组如式(9)所示：

(9)

式中：X为扰动后的参数值；X′为扰动后参数值的增量；X0为扰动前的参数值；i为虚数；w为压力波的角频率，Hz；k为波数，m-1。

2.4 模型求解

将辅助方程与控制方程联立，并忽略二阶小量，可将控制方程转换成另1种形式。

转换后的连续性方程组如式(10)所示：

(10)

转换后的动量守恒方程组如式(11)所示：

(11)

设定上述齐次线性方程组的系数矩阵为A，根据方程组有解的条件可以得到相应矩阵，如式(12)所示：

(12)

式(12)是1个关于波数k的一元四次方程。通过高斯消元法对式(12)进行求解，可以得到2个根，1个根的实部为正数，另1个根的实部为负数，分别表示压力波沿下游和上游方向传播。根据这2个根可求得压力波在气液两相流中的传播速度和衰减系数如式(13)所示：

(13)

式中：vpw为压力波在气液两相流中的传播速度，m/s；ηpw为压力波在气液两相流中的衰减系数，dB/m；Re(k)为波数的实部；Im(k)为波数的虚部。

2.5 模型验证

在对数学模型的准确性进行验证时，主要将模型的计算结果与Henry等和Huang等所获得的实验数据进行对比。Henry与Huang实验所用的主要参数如表1和表2所示。数学模型的验证结果如图2所示。

表1 Henry等对传播速度进行测试时的实验参数Table 1 Experimental parameters when testing propagation velocity by Henry et al.

表2 Huang等对衰减系数进行测试时的实验参数Table 2 Experimental parameters when testing attenuation coefficient by Huang et al.

从图2中可以看到，在相同的条件下，所建立的数学模型的计算结果与Henry等和Huang等所获得的实验数据具有较高的吻合度。因此，本文数学模型的计算结果是准确可靠的。

图2 数学模型的验证结果Fig.2 Verification results of mathematical model

3 影响因素分析

3.1 基本参数设置

使用数学模型对压力波在环空气液两相流中的传播特性进行模拟时所用到的参数如表3所示。

表3 压力波传播特性模拟所用参数值Table 3 Parameter values used when simulating propagation characteristics of pressure wave

3.2 含气率的影响

设定压力波的角频率为50 Hz，系统压力分别为0.50，0.80，1.10，1.40，1.70，2.00 MPa。所得到的压力波传播速度与衰减系数的变化趋势如图3所示。

图3 含气率对传播速度和衰减系数的影响Fig.3 Influence of gas volume fraction on propagation velocity and attenuation coefficient

从图3中可以看到，当含气率小于10%时，随着含气率的增加，压力波的传播速度持续降低，而压力波的衰减系数则缓慢升高。当含气率大于10%时，随着含气率的增加，压力波的传播速度逐渐趋于稳定，而衰减系数继续缓慢升高。

3.3 角频率的影响

设定系统压力为0.50 MPa，含气率分别为0.05，0.10，0.15，0.20，0.25，0.30。所得到的压力波传播速度与衰减系数的变化趋势如图4所示。

从图4中可以看到，当压力波的角频率小于100 Hz时，随着角频率的增加，压力波的传播速度和衰减系数持续增加。当压力波的角频率大于100 Hz时，压力波的传播速度和衰减系数逐渐趋于一定值。

图4 角频率对传播速度和衰减系数的影响Fig.4 Influence of angular frequency on propagation velocity and attenuation coefficient

3.4 系统压力的影响

设定压力波的角频率为50 Hz，含气率分别为0.05，0.10，0.15，0.20，0.25，0.30。所得到的压力波传播速度与衰减系数的变化趋势如图5所示。

从图5中可以看到，当系统压力小于2 MPa时，随着系统压力的增加，压力波的传播速度逐渐增加，而压力波的衰减系数逐渐减小。当系统压力大于2 MPa时，随着系统压力的增加，压力波的传播速度和衰减系数逐渐趋于稳定。

图5 系统压力对传播速度和衰减系数的影响Fig.5 Influence of system pressure on propagation velocity and attenuation coefficient

3.5 虚拟质量力的影响

设定含气率为0.02，系统压力为0.70 MPa，虚拟质量力强度系数分别为0.00，0.10，0.20，0.30，0.40，0.50。所得到的压力波传播速度与衰减系数的变化趋势如图6所示。

从图6中可以看到，在考虑了虚拟质量力的影响以后，压力波在相同条件下的传播速度要小于理想情况，而衰减系数要大于理想情况。虚拟质量力越大，压力波的传播速度越低，衰减系数越高。

图6 虚拟质量力对传播速度和衰减系数的影响Fig.6 Influence of virtual mass force on propagation velocity and attenuation coefficient

3.6 拖曳力的影响

设定含气率为0.02，系统压力为0.70 MPa，拖曳系数分别为0.00，0.10，0.20，0.30，0.40，0.50。所得到的压力波传播速度与衰减系数的变化趋势如图7所示。

从图7中可以看到，在考虑了拖曳力的影响以后，压力波在相同条件下的传播速度要小于理想情况，而衰减系数要大于理想情况。拖曳力越大，压力波的传播速度越低，衰减系数越高。

图7 拖曳力对传播速度和衰减系数的影响Fig.7 Influence of drag force on propagation velocity and attenuation coefficient

3.7 剪切应力的影响

设定系统压力为1.80 MPa，压力波的角频率为50 Hz，剪切应力系数分别为0.00，0.10，0.20，0.30，0.40，0.50。所得到的压力波传播速度与衰减系数的变化趋势如图8所示。

从图8中可以看到，在考虑了剪切应力的影响以后，压力波在相同条件下的传播速度要小于理想情况，而衰减系数要大于理想情况。剪切应力越大，压力波的传播速度越低，衰减系数越高。

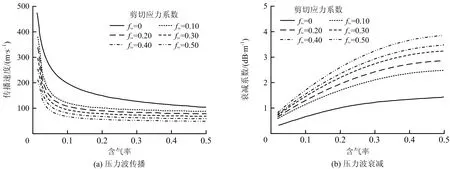
图8 剪切应力对传播速度和衰减系数的影响Fig.8 Influence of shear stress on propagation velocity and attenuation coefficient

4 现场应用分析

通过前文所建立的数学模型对相应作业条件下压力波在井筒各节点上的传播与衰减特性进行计算，即可分别得到压力波在2条路径传播时所用的时间。这也是压力波检测法应用于现场作业的主要理论依据。本文针对四川西部1口实钻井在应用MWD压力波信号进行气侵检测时的应用效果进行分析。图9是实钻井的井身结构示意。

图9 井身结构示意Fig.9 Schematic diagram of well structure

通过本文所建立的数学模型对不同气侵率条件下压力波在井筒各节点上的传播与衰减特性进行计算，所得结果如图10所示。

图10 不同气侵率下井筒各节点上的传播速度与衰减系数Fig.10 Propagation velocities and attenuation coefficients at each node of wellbore under different gas-kick rates

从图10中可以看到，在相同井深处的井筒节点上，气侵率越大，压力波的传播速度越低，衰减系数越大。这主要是因为，气侵率越大，井筒中气液两相间的动量和能量的交换程度越剧烈，且气液两相流的可压缩性增大，从而造成压力波的能量耗散增加，传播速度减慢。

该井在5 174 m和5 328 m发生气侵时的现场检测结果如图11所示。

图11 气侵的现场检测结果Fig.11 Results of gas-kick field detection

从图11中可以看到，相比于常规的全烃量检测法，压力波检测法能够在很大程度上更早地检测到气侵的发生。因此，使用压力波对早期气侵进行检测，能够进一步提高钻井作业的安全性。

5 结论

1)当含气率小于10%时，随着含气率的增加，压力波的传播速度持续降低，而衰减系数则缓慢升高；当含气率大于10%时，随着含气率的增加，传播速度逐渐趋于稳定，而衰减系数继续缓慢升高。

2)当压力波的角频率小于100 Hz时，随着角频率的增加，压力波的传播速度和衰减系数持续增加；当压力波的角频率大于100 Hz时，压力波的传播速度和衰减系数逐渐趋于一定值。

3)当系统压力小于2 MPa时，随着系统压力的增加，压力波的传播速度逐渐增加，而衰减系数逐渐减小；当系统压力大于2 MPa时，随着系统压力的增加，压力波的传播速度和衰减系数逐渐趋于稳定。

4)在考虑了虚拟质量力、拖曳力和剪切应力的影响后，压力波的传播速度要低于理想情况，而衰减系数要高于理想情况。

5)相比于常规的全烃量检测法，压力波检测法能够在很大程度上更早地检测到气侵的发生，能够进一步提高钻井作业的安全性。