海上溢油应急物资调度双目标规划模型*

2022-03-07徐文辉李亚东

中国安全生产科学技术 2022年1期

李晶，徐文辉，李亚东

(大连海事大学交通运输工程学院，辽宁大连 116026)

0 引言

自20世纪70年代以来，我国共发生溢油事故约2 200起，总溢油量约22 000 t，溢油事故给海洋生态环境造成巨大破坏,同时带来巨大经济损失。因此，在面对突发溢油事故时，政府应合理选择出救点，恰当规划应急物资调度方案，降低溢油事故造成的不利影响。

针对海上应急事故特点进行物资调度的研究尚处于起步阶段：王军等[1]考虑海上环境等因素对海上突发公共安全事故的影响，构建以满足物资供应为目标的应急物资调度模型；文献[2-3] 考虑到需求点对应急物资的需求不确定性，用三角模糊数描述应急物资需求量等不确定因素。

相对海上事故，陆上突发公共安全事件物资调度研究比较成熟：文献[4-8]根据应急事故特点提出“多出救点和单一需求点”的应急物资调度模型；针对部分突发事故有多个需求点，文献[9-11]提出“多出救点、多需求点及需求点对应急物资的需求量确定”；文献[12-15]提出“多出救点、多需求点及需求点对应急物资的需求量不确定”的应急物资调度优化模型。

综上，在海上突发溢油事故情况下，现有研究多采用模糊规划或随机规划描述需求不确定性，而模糊规划则需要根据决策者经验得到不确定参数的模糊隶属函数，具有主观性；随机规划需要假设不确定因素服从某种概率分布，结果不够准确。

突发溢油事故下，应急物资应以最短时间抵达需求点，但在实际应急调度过程中决策者通常需要考虑应急成本，从而选择合适出救点和救援路径，2个目标相互冲突，决策者需要在2者之间平衡利弊，以寻求最佳溢油应急方案。因此，本文充分考虑海上溢油事故特点，采用鲁棒优化方法处理受灾点对物资需求量的不确定，将溢油点漂移特性纳入应急物资调度模型，构建应急成本最小、应急时间最短的物资调度双目标规划模型，并用NSGA-Ⅱ算法进行求解。

1 问题描述

溢油事故发生在风速较大、水流湍急的海面上时，油膜发生漂移，形成新的“需求点”，即漂移点。应急基地救援示意如图1所示，其中实线为救援路径，虚线为油膜漂移路径。

图1 应急基地救援示意Fig.1 Schematic diagram of emergency base rescue

为将溢油事故造成的损失降至最低，考虑溢油量不确定，首先选择到达“漂移点”时间最短的应急基地，以阻断油膜漂移路径，使“漂移点”地理位置不发生变化，同时对溢油点和漂移点展开后续救援。本文主要针对需求不确定情况下，多出救点、多需求点的应急物资调度问题展开研究。

针对事故特点，做出以下4点假设：

1)溢油事故发生后，海风风向和水流方向不变，风速等级和水流速度大小不变。

2)应急基地可以供应多个需求点物资，但基地之间不可以进行物资转运。

3)漂移点一旦受到首批应急物资的救助，其地理位置将不会发生变动。

4)引用“救助资源包”这一概念，将溢油所需救援物资进行整合，组成1个救助资源包，且单个“救助资源包”可处理1 kg的油污。

2 模型构建

2.1 “漂移点”确定

以假设3)为依据，在首批应急物资到达漂移点之前，对油膜漂移动态过程进行求解，确定漂移点位置。

根据油膜漂移速度、船舶速度及应急基地至溢油点距离，利用式(1)求得溢油点漂移时间，以确定溢油点漂移位置：

(D3)2=(D1)2+(D2)2-2D1D2cos(θ)

(1)

式中：D1为油膜漂移距离，m；D2为应急基地与溢油点之间距离，m；D3为应急基地与漂移点间距离，m；θ为基地至溢油点路径与漂移路径两边夹角，(°)。

船舶在水中实际移动速度如式(2)所示：

Vz=V-(0.745h-0.257qh)(1.0-1.35×10-6DV)

(2)

式中：Vz为水中实际行驶速度，kn；V为船舶在静水中的速度，kn；h为波高，m；q为船首方向与波浪来向之夹角(°)；D为船舶排水量，t。

油膜漂移速度如式(3)所示：

Vo=K×Vw+Vf

(3)

式中：K为风力系数，取0.035；VW为风速，kn；Vf为水的表面流速，kn。

油膜漂移距离如式(4)所示：

(4)

式中：Vo为油膜漂移速度，kn；Δt为油膜漂移时间，h。

2.2 考虑漂移点的物资调度模型构建

溢油事故发生后，若油污不能及时清理，将在风力和水流共同作用下发生漂移，扩散至更广阔的海域，以应急时间最少为目标函数，同时考虑救援成本，构建应急成本最小和应急时间最少的双目标需求不确定应急物资调度模型如式(5)～(15)所示。其中成本函数如式(5)所示：

(5)

式中：C为应急成本，元；Dij为应急基地i与需求点j之间的距离，m；xijs为是否使用救助船舶s将应急物资从i点运至j点；f为船舶每海里行驶的油耗成本,元；z为随应急救援时间延长，溢油导致的环境污染治理成本，元,本文取值1 000 000。时间函数应急时间T如式(6)所示：

(6)

模型约束条件如式(7)～(15)所示：

ri≥0,∀i∈I

(7)

Dij≥0,∀i∈I,j∈J

(8)

(9)

(10)

(11)

xijs=0，i∈I,j∈I,s∈S

(12)

xi={0,1},∀i∈I

(13)

xijs={0,1},∀i∈I,j∈J,s∈S

(14)

yijs≥0,∀i∈I,j∈J,s∈S

(15)

模型中式(5)～(6)为目标函数，式(5)为成本函数，表示各出救点向需求点运送物资的总运输费用与油膜给环境带来的损失之和最小；式(6)为时间函数，即各船从出救点向需求点的总救援时间最短。

式(7)～(15)为约束条件：约束(7)指应急基地i的救援物资库存量不小于0；约束(8)指应急基地i与需求点j的距离不小于0；约束(9)指从各应急基地运至需求点的应急物资量不超过其库存；约束(10)指船舶的容量约束；约束(11)指充分满足需求点的物资需求量；约束(12)指各应急基地间的救援物资不可以相互转运；约束(13)是0～1变量，如果选择应急基地i为出救点，则xi为1，否则为0；约束(14)是0～1变量，如果选择使用船舶s将物资从基地i运至需求点j，则xijs为1，否则为0；约束(15)指船舶s运输的物资量不小于0。

2.3 基于鲁棒优化的需求量不确定性处理

海上突发溢油事故的溢油量具有不确定性，使用机会约束规划模型和模糊规划描述应急物资需求的不确定性具有很大的局限性，但鲁棒优化具有以下2个优点：鲁棒优化在建模过程中充分考虑了不确定性，且不需要不确定参数的分布模型或其模糊隶属函数；鲁棒优化的约束条件是严格成立的，即只要不确定参数属于不确定集合，所求出的解就满足约束条件。因此，本文使用鲁棒优化方法处理需求不确定性。

(16)

式中：dj为需求点j的名义需求量；aj为需求点j的需求扰动量，aj=εjdj；εj为扰动比例；uj为不确定性因子。

不确定需求集合如式(17)所示：

(17)

式中：Γu表示需求不确定集合的不确定水平参数，客观衡量约束条件的保守程度，体现决策者的风险偏好程度，Γu越小，表明模型越不保守，Γu∈[0,n]；n为模型中不确定需求点的个数(n可取小数)[15]。将约束(11)进行鲁棒优化得到约束(18)～(19)：

(18)

(19)

因dj是名义需求，不受不确定性影响，所以将约束(18)转化成约束(20)：

(20)

因约束(20)是非线性规划，不易求解，引入对偶变量yj，zj进行对偶转化，将约束(19)～(20)转化为约束(21)～(23)。

(21)

yj+zj≥εjdj,∀j∈J

(22)

yj≥0,zj≥0,∀j∈J

(23)

约束条件(11)经鲁棒优化处理后，转化为约束条件如(21)～(23)所示。

3 NSGA-Ⅱ算法设计

3.1 NSGA-Ⅱ

针对双目标应急物资调度模型，本文用NSGA-Ⅱ算法求解，由GA改进而来，需经历种群初始化、选择、交叉、变异、迭代等过程。与GA最大区别在于在算法中加入非支配排序和拥挤度比较；引入精英策略，保证个体的多样性。

3.2 编码

本文使用二进制编码，根据问题特点及规模，生成的染色体有22个基因，如图2所示。将染色体分成11部分，每部分代表1个出救点，且有2个基因，基因位1代表是否将物资运至溢油点；基因位2代表是否将物资运至漂移点；若2个基因均为1，表示既将物资运至溢油点，也将物资运至漂移点。图2中染色体表示将应急物资从基地2运至溢油点，从基地5运至漂移点，并且从基地10运往溢油点和漂移点。

图2 染色体编码示意Fig.2 Schematic diagram of chromosome coding

3.3 种群初始化、选择、交叉及变异

1)种群初始化。本文种群中染色体为随机生成，每个应急基地都有几率将物资运往需求点，但随机产生的染色体应满足模型中的约束条件。

2)选择。采用锦标赛选择策略，基于拥挤比较算子及非支配排序等级。拥挤比较算子在算法中可以将选择过程导向均匀分布的Pareto最优前沿面，在2个不同支配等级排名的解中，选取排名较低的解，若2个解属于同一Pareto前沿面，选取处于非拥挤区域的解。

3)交叉。选取邻近的2个父代染色体寻找交叉点，进行单点交叉，单点交叉能较好地保存父亲的优良基因，假如取4号基因位为交叉位置，染色体A和染色体B交叉所得染色体为A′和B′，如式(24)所示：

(24)

4)变异。本文采取的变异方式为随机变异，在众多染色体中，以一定概率选择需要变异的染色体，随机选择该染色体中的1个或多个基因进行变异。例如，选择染色体C的第2个和第7个基因进行变异，形成新的染色体为C′，如式(25)所示：

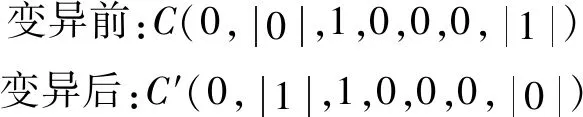
(25)

4 算例分析

4.1 相关数据

本文假设蓬莱溢油事件名义溢油量为250 t；根据第4)条假设可知“救助资源包”的名义需求量为250 000个；假设溢油点对“救助资源包”的名义需求量为150 000个，“漂移点”的名义需求量为100 000个；根据商务部数据显示，救助船舶行驶每海里的成本f为315元。各备选应急基地基本信息见表1。

表1 备选应急基地基本信息Table 1 Basic information of alternative emergency bases

2011年蓬莱石油泄漏事故发生时，渤海海域风向为偏南风，平均风速为2.214 kn，水流流速较小，取船首与浪向夹角q为0°，水流流速Vf取0 kn[16]，浪高0.6 m；应急救助船舶平均航行速度为21 kn，总吨位D=4 000 t(吨)，托运力100 t。利用式(2)计算船舶实际行驶速度为20.164 kn，式(3)计算出油膜漂移速度为0.279 kn。

4.2 模型结果

1)“漂移点”位置确定

“漂移点”位置确定主要包括以下3个步骤：

①利用应急基地和溢油点经纬度(38.373N，120.118E)求出其之间的距离。

②由于溢油事故发生时风向为南风，且水流对油膜漂移的影响可忽略不计，可知漂移点的经度与溢油点的经度一致。首先假设 “拟定漂移点”的经纬度为(39.373N，120.118E)，然后利用ArcGIS软件将溢油点、拟定漂移点和应急基地作为三角形3个顶点，最后求出以溢油点位顶点的夹角θ。

③将船舶实际速度、油膜漂移速度、夹角θ及应急基地与溢油点之间的距离带入式(1)，得到应急基地至漂移点的时间，结果显示东营至漂移点的时间最短为2.838 h。

因此，首先选择将存放在东营应急基地的物资运往漂移点，以阻碍油膜继续漂移，减少对生态环境的破坏，利用式(4)求得溢油点漂移的最长距离为1 466.784 m，求得漂移点的经纬度为(38.387145 N，120.118486 E)。

2)调度结果

本文用Matlab2016a进行计算，而需求点对“救助资源包”的实际需求量取决于决策者对风险水平的偏好程度，其在鲁棒模型中可以从Γu和εj的取值大小体现出来。由于本文的需求点只有2个，因此，Γu和εj在本文中的取值集合分别为{0，0.5，1，1.5，2}和{3%，5%，10%}；取种群规模为200，迭代次数为1 000，得到的调度结果见表2。当Γ为0时，无论扰动比例取3%、5%、10%，其所代表的方案均为：3-a,7-b,8-a,9-b,11-a。表示将应急物资从营口运至溢油点、莱州运至漂移点、潍坊运至溢油点、东营运至漂移点和葫芦岛运至溢油点。

表2 物资调度方案Table 2 Schemes of materials dispatching

注：表中数字所代表的基地序号见表1；a，b分别指溢油点和漂移点。

应急调度具有弱经济性的特点，势必以效率优先，但实际过程中会受严格资金约束限制，所以帕累托解可为决策者提供参考，决策者可根据实际应急事故，选择相应应急调度方案，名义模型结果示意如图3所示。由图3可知，得到的解具有前沿面，若决策者判断此事故为重大事故，则选择应急时间较短的调度方案，否则选择应急成本和应急时间综合结果较优的应急物资调度方案。

图3 名义模型结果Fig.3 Results of nominal model

3)结果分析

虽然不同扰动比例及不确定水平下的应急成本和时间不同，但应急出救点的选择方案共有8个，其中某个方案被使用了8次，说明该模型的鲁棒性较好，优化方案对参数扰动不敏感。

根据模型，不同风险类型偏好的决策者可以得到相应的救援方案，方案见表2。如果决策者为风险追求偏好，则可选取较小的Γu和εj，得到相应的应急方案，该方案应急成本较小并且应急时间较少；如果决策者为风险规避型，则可选取较大的Γu和εj，但是会以较高的应急成本和较长的应急时间为代价；如果决策者可接受的风险水平介于2者之间，则选择折中方案。在不同扰动比例εj和不确定水平Γu下，2个函数的目标值变化如图4所示。当Γu=0时，鲁棒物资调度模型等价于名义模型，应急成本C=742 770.8元，应急时间T=24.31 h。Γu相同时，随εj变大，2个目标函数值上升幅度呈现从小到大的趋势；当εj为3%时，随Γu增大，目标函数上升趋势并不明显；当εj为5%时，随Γu增大，目标函数值呈现较慢的上升趋势；当εj为10%时，随Γu的增大，目标函数上升趋势比较明显，应急成本相对名义模型的增加率分别为0.6%、1.7%、2.3%和5.1%，应急时间相对名义模型的增加率分别为1.3%、5.6%、10.2%和21.4%。Γu和εj在一定程度上可以衡量决策者的风险偏好，因此决策者可根据自己对不确定风险水平的偏好程度选择相应的Γu和εj。

图4 需求不确定下的目标函数值Fig.4 Objective function values under uncertainty of demand

在不同Γu和εj情况下获得的物资调度方案见表2。随Γu和εj的变大，为满足溢油点和漂移点对应急物资的需求，采取以下3种措施：①当原有方案能满足现在的需求，则原来的方案保持不变。②当原有出救点能满足需求，但物资调度分布的数量不能满足受灾点对应急物资的需求量，则应急出救点的选择保持不变，将调度方案重新规划。③当原有应急物资调度方案不能满足需求点对应急物资的需求时，系统会重新进行计算评估获得新的救援方案。