坡地建筑外立面火灾温度演化研究*

王心凯，何 清，唐 飞

(1.中国科学技术大学 管理学院，安徽 合肥 230026；2.安徽工业大学 能源与环境学院，安徽 马鞍山 243002；3.中国科学技术大学 火灾科学国家重点实验室，安徽 合肥 230026)

0 引言

21世纪以来，随着城镇化的加快，建筑业得到了快速的发展，各式各样的建筑不断增加。但随之而来的，建筑火灾事故往往会给人们的生命财产安全造成重大损失。因此，建筑火灾安全领域引发了社会的关注且已经成为应急管理领域的重要研究热点之一[1-3]，而对建筑外立面火羽流特征参数演化规律的研究就显得尤为重要。

国内外学者针对建筑外立面溢出火羽流特征参数演化规律开展了大量研究[4-16]。对于自由边界条件的受限空间开口火溢流，Yokoi[7]在1960年首次针对小尺寸燃烧室0.4 m×0.4 m×0.2 m(长×宽×高)火灾，研究了通过开口溢出的热羽流竖向温度分布特征。Lee等[10]和Delichatsios等[12]设计了1个“长走廊型”开口火溢流实验台，研究了不同火源位置和不同长宽开口条件下的燃烧室内外温度分布规律、燃烧室外的热流密度变化规律以及火焰高度。随后，唐飞[13]进一步考虑虚拟点源理论，对外立面火羽流竖向温度分布模型进行了有效修正。

由于自然地形或环境条件的限制，一些建筑物必须建在山坡上。例如中国重庆市大多数高层建筑都建在山坡上。建筑附近的山坡将构成另1种特殊的约束边界条件。Tang等[14]，Xu等[15]通过实验研究了不同倾斜坡度下的矩形开口火溢流火焰燃烧特性，得出了倾斜墙面对于温度分布、热流分布和火焰形态的演化规律。但是，上述外立面火羽流研究主要针对矩形开口(窗户)建立。

随着建筑的多元化的发展，圆形窗口(开口)建筑逐渐增多。关于圆形开口建筑火灾的研究仍然相当缺乏。目前，Zhang等[16]利用缩尺寸实验研究并揭示了圆形开口建筑火灾建筑室内气体温度分布规律以及外立面火焰演化特性。然而，国内外尚没有对圆形开口建筑火灾外立面火羽流温度分布研究的相关报道。针对这一特殊火行为特征，围绕山地建筑火灾圆形开口外立面火羽流温度演化开展研究，对坡地建筑火灾经典理论进行有效补充，为圆形窗口建筑消防安全设计提供实验参考依据。

通过小尺寸实验，分析不同倾斜挡墙(坡地)下的圆形开口建筑火灾外立面溢出热羽流竖向温度演化规律，并结合无量纲分析，建立考虑不同的倾斜坡度、不同的圆形开口、不同的火源功率等变量时的热羽流竖向温度预测模型。

1 实验设计

1.1 实验装置

图1为实验装置示意，主要包括缩尺寸建筑模型、燃烧系统及温度数据采集系统3部分。通过实验可获取燃烧室内热气体温度和腔室外立面热羽流温度数据。

图1 实验装置Fig.1 Experiment device

1)缩尺寸建筑腔室火灾模型。采用尺寸为长0.5 m宽0.3 m高0.40 m的长方体燃烧室模拟建筑室内火灾，外部为2 mm厚的钢板，内衬有8 mm厚的防火石棉。在模拟腔室上设置单一圆形开口，1.80 m×1.70 m的防火板紧贴开口模拟建筑外立面，2.4 m×1.70 m的防火板模拟建筑倾斜挡墙。在燃烧室侧壁和外立面上钻有直径2 mm的小孔以布置热电偶。

2)火源燃烧装置。在燃烧室地板正中央设置边长为0.16 m的多孔气体燃烧器，其下表面与地板齐平，小孔间距为8 mm。选择丙烷气体作燃料，丙烷气体由气瓶通过减压阀和质量流量计输送至燃烧器。通过调节质量流量计可控制丙烷气体流量，质量流量计的精度为0.1 L/min。

3)温度数据采集系统。在燃烧室内外角落分别设置3串6个直径为1 mm的K型热电偶，距离相邻侧墙表面0.05 m，内外角落的热电偶分别位于顶棚下方0.05 m和0.15 m处，用于测量室内热气体温度。在外立面上设置4个直径为1 mm的K型热电偶，以测量外立面热羽流温度。热电偶位于圆形开口中心线正上方，距离外立面0.005 m，相邻2个测点间距为0.10 m，最下方热电偶与燃烧室外部顶棚距离为0.9 m。实验中热电偶将温度信号转化为电信号，经热电偶导线输送到7018数据采集模块，最后由电脑记录并输出温度数据。

1.2 实验工况设计

实验中，根据其流入腔室内的空气质量流率和热烟气流出的质量流率[17]相同的办法利用MATLAB计算出临界溢出的火源功率，如表1所示。文中所有工况火焰均能完全溢出。采用3个不同通风因子的开口用以模拟不同建筑圆形门窗尺寸,每1个开口尺寸下采用3种不同的火源热释放速率以及不同倾斜角度侧墙。

如表1所示，27个实验工况涵盖了不同实验条件的组合。每次实验重复3次，且实验重复性较好。环境温度为(39±5)℃。

表1 实验工况Table 1 Experimental conditions

2 实验结果与讨论

2.1 燃烧腔室内温度

图2为无倾斜挡墙作用下的典型圆形开口工况燃烧室内气体温度(Tg)随火焰功率的变化关系。由图2可知，在稳定燃烧状态下，对于确定的开口尺寸，燃烧室内6个热电偶测得的热气体温度基本保持一致，每个测点温度随火源功率变化趋于稳定。

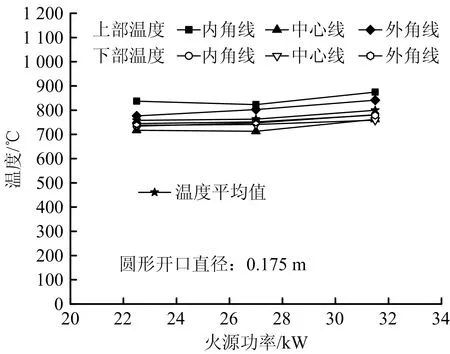
图2 开口0.175 m室内气体温度随火源功率变化Fig.2 Change of indoor gas temperature with fire source power under opening size of 0.175 m

图3为圆形开口直径为0.2 m工况建筑燃烧室内火羽流温度(Tg)随外部倾斜挡墙角度的变化关系。从图3中看出，对于确定开口的燃烧室，燃烧室内的温度不随着倾斜挡墙的角度而变化，这和矩形溢流开口下的腔室外温度分布规律类似[15]。

图3 开口0.2 m室内火羽流温度随倾斜挡墙坡度变化Fig.3 Change of indoor fire flume temperature with slope of inclined retaining wall under opening size of 0.2 m

2.2 无倾斜挡墙下外立面热羽流竖向温度分布

对于矩形开口，开口中性面位置一般为0.4倍的开口高度[10]。对于圆形开口，由于圆形面积在中部变化较大，使得圆形开口中性面对比矩形开口较高，其开口中性面位置(Zn)在大约0.41D～0.44D范围内[16]。本文选取0.42D的位置作为参考高度，以Z-Zn表示中性面到至测量热电偶的距离。图4为无倾斜挡墙下不同圆形开口尺寸建筑火灾外立面热羽流竖向温度分布图。

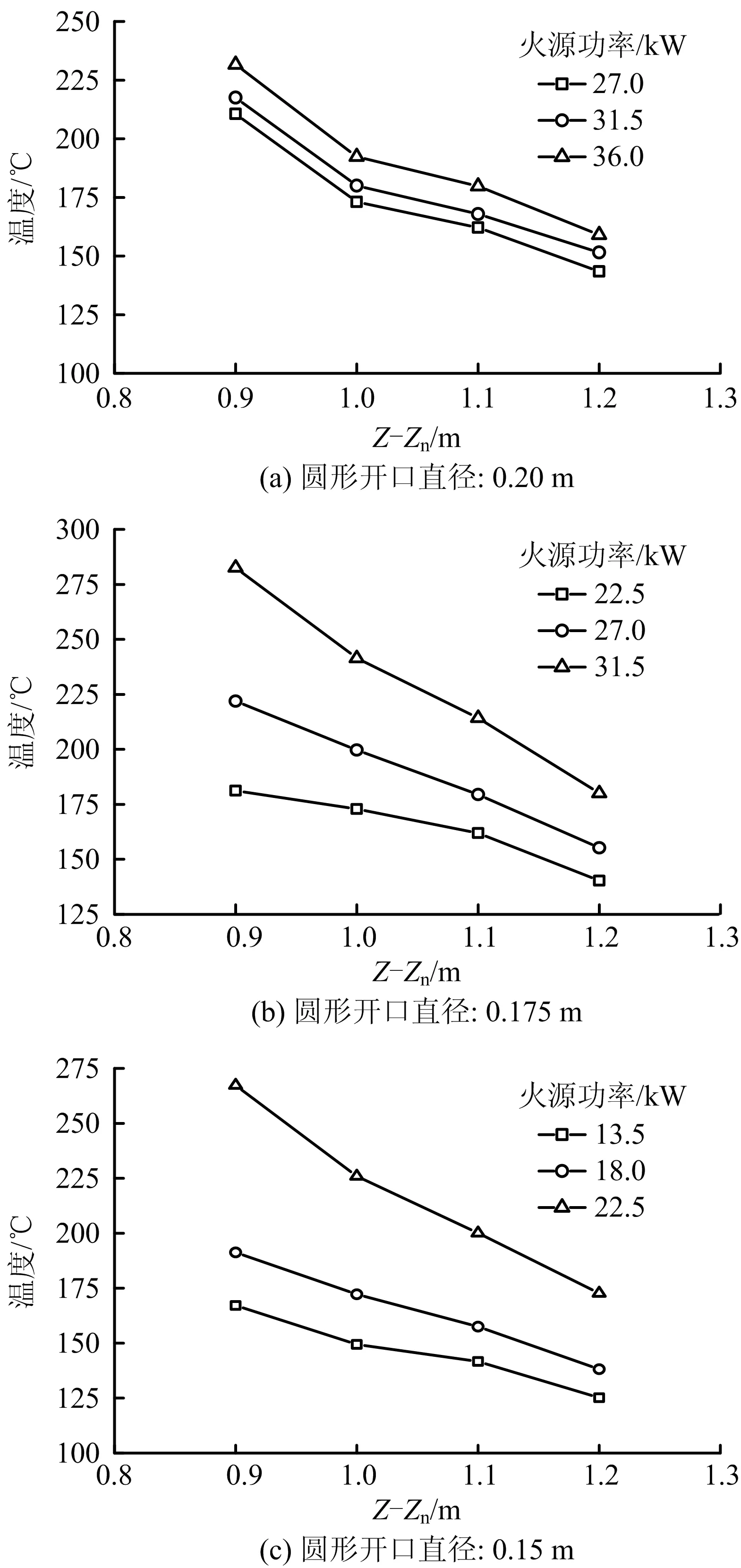
图4 不同开口尺寸和火源功率下外立面热羽流竖向温度分布Fig.4 Distribution of vertical temperature of external facade thermal plume under different opening sizes and fire source power

从图4可以得出：1)在一定的火源功率和开口尺寸相同条件下，热羽流温度随竖直高度的增加而降低。2)对于确定的圆形开口，在相同竖直高度位置的热羽流温度随火源功率增大而升高。3)当火源功率和竖直高度一定时，由于开口尺寸越小的工况腔室外的火源功率越大，导致热羽流温度越高。圆形开口建筑外立面竖向热羽流温度演化过程与矩形开口火溢流工况[13,14]基本一致。

依据Lee的研究[11]，外立面火羽流演化特性受开口形状和尺寸的影响。Delichatsios等[12]通过理论分析得到与矩形开口尺寸相关的特征长度，基于实验数据建立了矩形开口溢出热羽流温度无量纲预测模型如式(1)所示：

(1)

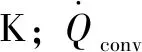
结合图4可知，将公式(1)中特征长度替换为圆形开口尺寸相关的特征长度，可表征圆形开口外立面热羽流温度。对外立面热羽流温升进行无量纲处理，做出外立面热羽流竖向无量纲温升Θ与无量纲竖直高度(Z-Zn)/D的变化关系，如图5所示。基于实验温度数据拟合可得到圆形开口火溢流建筑外立面热羽流竖向温升预测公式如式(2)所示：

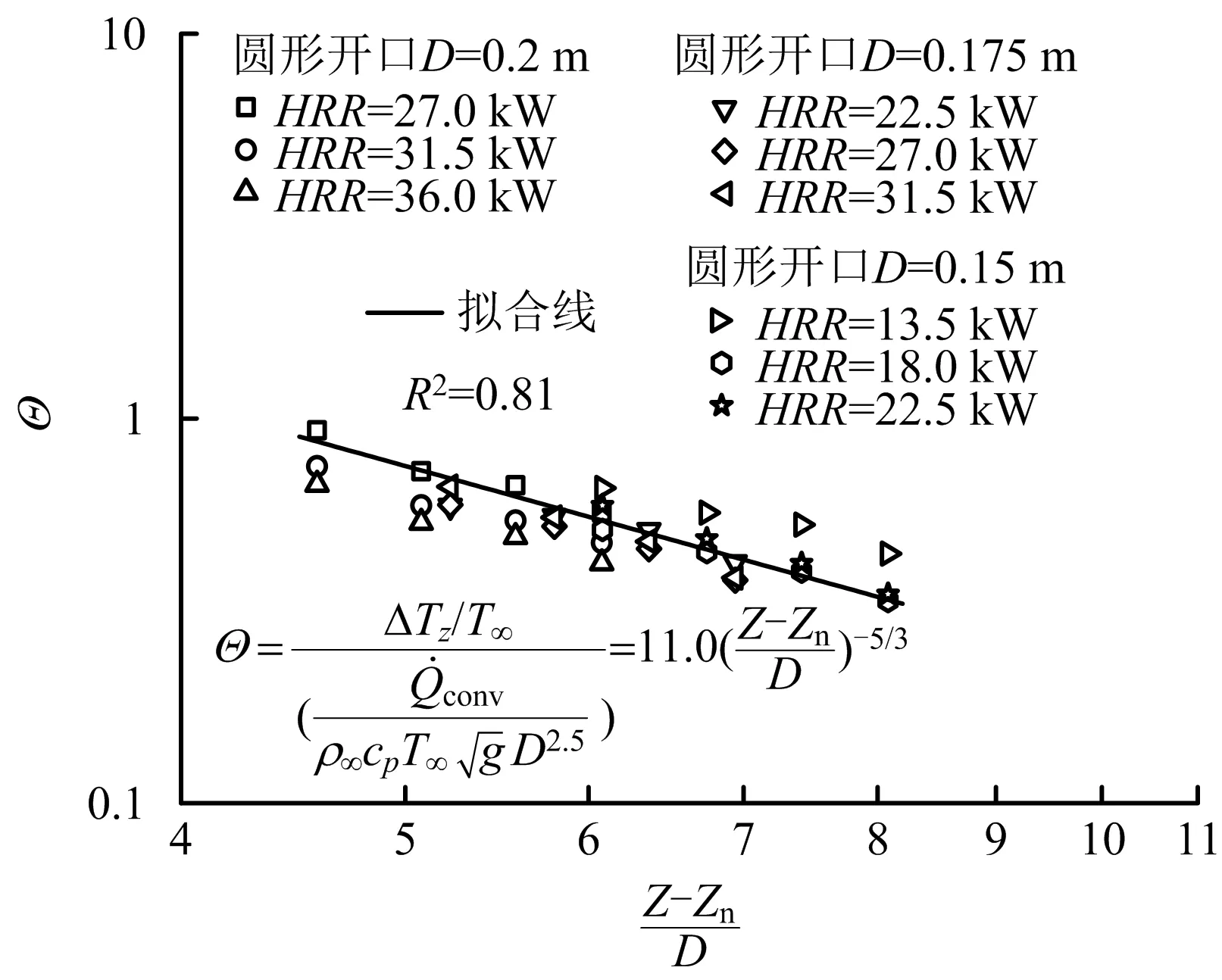
图5 无倾斜挡墙下外立面热羽流无量纲温升与无量纲竖直高度的拟合关系Fig.5 Fitting relationship of dimensionless temperature rise of external facade thermal plume and dimensionless vertical height without inclined retaining wall

(2)

2.3 倾斜挡墙下外立面热羽流竖向温度分布

图6为倾斜挡墙下不同圆形开口尺寸建筑火灾外立面热羽流竖向温度分布图。从图6可以得出：在相同开口、火焰功率下，同一位置的竖向随着倾斜挡墙角度的增加而增加，且增加速率变大。这个演化规律和矩形开口溢出的温度分布规律类似[13]。随着倾斜角度的增加，外立面的的火羽流迅速增强，侧墙与倾斜挡墙之间的空气变少，燃烧室外部新鲜空气被卷到中性面以下，这种情况类似于烟囱效应。从而导致从燃烧室溢出的火焰在较大的倾斜角度下迅速沿侧墙散开，形成较高的火焰高度，使得温度增加。

图6 不同倾斜挡墙下外立面热羽流竖向温度分布Fig.6 Distribution of vertical temperature of external facade thermal plume under different inclined retaining walls

采用和无倾斜挡墙下的圆形开口火溢流外立面热羽流竖向温度分布预测公式同样的方法，得到倾斜挡墙为60°时建筑外立面热羽流竖向温升预测公式如式(3)所示，倾斜角度为80°时预测公式如式(4)所示。

(3)

(4)

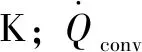
倾斜挡墙的影响可以用余弦函数来量化倾斜挡墙的影响因子I。在没有倾斜挡墙下影响因子I为1。如图7所示。从图7数据拟合得到不同倾斜挡墙下的圆形开口火溢流外立面热羽流影响因子如式(5)所示：

图7 影响因子I和倾斜挡墙坡度联系Fig.7 Correlation between impact factor I and slope of inclined retaining wall

I=-0.24cos(θ)+1.24

(5)

式中：I为不同倾斜挡墙(坡地)影响因子。

因此，可以得到倾斜挡墙作用下的圆形开口火溢流建筑外立面热羽流竖向温升预测公式如式(6)所示：

(6)

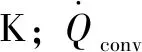
图8为基于拟合公式(6)得到的外立面热羽流温度预测值与实验结果的对比关系。由图8可知，数据的相对偏差在20%的范围内，因此外立面热羽流温度预测值与实验结果表现出良好的一致性。

图8 建筑外立面热羽流温度预测值与实验结果的对比Fig.8 Comparison between predicted values and experimental results of thermal plume temperature on external facade of building

3 结论

本文针对坡地建筑外立面火灾这一特殊火行为特征，开展了不同坡度角度情况下圆形开口建筑火溢流实验研究，测量和分析不同倾斜挡墙(坡地)下的圆形开口建筑火灾外立面溢出热羽流竖向温度演化规律，具体结论如下：

1)当腔室的开口尺寸和火源功率一定时，在稳定燃烧状态下圆形开口燃烧室内温度基本不随着外面倾斜挡墙(坡地)存在而改变。

2)当开口尺寸和火源功率一定时，同一竖向位置处圆形开口外立面溢出热羽流竖向温度随着倾斜挡墙角度的增加而增加。

3)基于矩形开口外立面溢出热羽流竖向温度分布模型，结合无量纲理论分析与实验数据，建立不同倾斜挡墙作用下圆形开口建筑火灾外立面热羽流竖直温度预测模型。