考虑多性能约束的车辆主动前轮转向静态输出反馈控制

毛营忠， 冯智勇， 郭会茹

(武汉理工大学 现代汽车零部件技术湖北省重点实验室；汽车零部件技术湖北省协同创新中心， 武汉 430070)

近年来，以提高汽车安全性与舒适性为目标的先进驾驶人辅助系统(ADAS)已成为社会的研究热点.作为ADAS的关键技术之一，基于主动前轮转向(AFS)的人机共驾技术成为研究人员关注的重点.其中，AFS系统可根据车辆状态产生辅助转角对驾驶人转角进行修正，从而对横摆角速度进行跟踪控制来提高车辆的安全性与操纵稳定性.

由于车辆运动的强非线性和不确定性，AFS的控制方法一直是研究的重点[1].文献[2]基于模型预测控制(MPC)，通过对障碍物信息的实时检测来提高AFS系统的性能，从而提高车辆在不同轨迹下的跟踪效果.文献[3]将滑模控制方法应用到AFS中来实现对车辆期望横摆角速度的跟踪，提高了线控转向车辆的操作稳定性.文献[4]基于非线性轮胎模型提出一种新型线性时变MPC方法以提高极限工况下AFS车辆的稳定性.文献[5]提出了一种基于等价输入干扰估计的转向控制方法，通过估计器估计控制输入通道上的等效扰动来抑制外界干扰对车辆的影响.文献[6]由相平面法出发提出了AFS系统的介入原则，并设计了AFS系统的滑模变结构控制器，使紧急救援车辆的稳定性和安全性得到改善.文献[7]研究差动助力转向(DDAS)系统与AFS系统之间的协调控制问题，通过对电机转角与方向盘转矩的实时修正来降低两者之间的干扰，提高车辆的转向性能.

由于在抑制外部扰动与解决模型参数不确定性方面的优越性，鲁棒控制方法在AFS系统中的应用是目前的研究热点之一.文献[8]基于AFS系统的动态特性，考虑了车辆轮胎侧偏刚度的不确定性，设计一种参数能够综合鲁棒控制方法来提高车辆的路径跟踪性能.文献[9]提出一种模型跟踪与内模控制混合的二自由度鲁棒内模控制技术，解决了AFS控制中系统性能与鲁棒性之间的矛盾，提高了横摆角速度的跟踪性能.文献[10]基于鲁棒控制的方法设计了AFS系统的双环控制器以抑制干扰并改善车辆横摆角速度的跟踪性能.文献[11]考虑外界扰动与模型不确定性，提出一种基于线性矩阵不等式的AFS鲁棒控制方法，将横摆角速度与质心侧偏角作为约束以保证系统的鲁棒稳定性.文献[12]研究侧向风的干扰问题，考虑系统的H∞性能指标设计了AFS系统的输出反馈鲁棒控制器，同时避免了对车辆质心侧偏角的测量，降低了控制器的设计成本.文献[13]建立了归一化左互素因子分解(LCF)模型来处理模型中的不确定性，从而设计了考虑H∞性能约束的鲁棒控制器，并且加入了前馈控制，提高了系统的性能.文献[14]将含有不确定性参数的车辆模型转化为线性参数可变(LPV)模型，并设计了考虑系统的H2与H∞性能约束的静态输出反馈(SOF)鲁棒控制器.

SOF控制问题的求解一直是控制领域的难点和热点问题[15].文献[16]提出了一种坐标转换矩阵(CTM)优化方法来求解线性系统的最优H2SOF、H∞SOF控制问题.与已有的一些基于线性矩阵不等式(LMI)方法相比，该方法最突出的优点是能得到局部最优解.由于CTM方法不需要复杂的非线性优化技术，使用简单，可推广到不确定性系统的鲁棒控制问题.至今为止，CTM方法都是应用于线性连续或离散时不变系统，还从未应用于不确定性系统的研究.本文针对AFS系统控制问题，考虑轮胎侧偏刚度的不确定性，建立车辆侧向动力学多胞型模型.首次将CTM优化方法扩展应用于该类不确定性系统以解决基于SOF控制器的系统极点配置与H∞性能约束控制问题.通过对CTM的引入，并应用具有块三角结构的松弛变量，提出考虑参数不确定性的LMI充分条件.扩展运用CTM优化方法，通过对多个CTM的迭代更新来求解模型各个顶点处的LMI以得到最优SOF控制器，保证对期望横摆角速度的精确跟踪，提高车辆侧向稳定性.最后在MATLAB/Simulink和CarSim的联合仿真试验中验证所设计控制器的可行性与有效性.

1 模型的建立

1.1 二自由度车辆模型

主动转向系统主要研究车辆横向运动特征，考虑侧向与横摆两个方向的运动，建立二自由度车辆动力学模型如图1所示.其中：vx和vy分别为车辆的纵向与侧向速度；v为车辆实际速度；lf和lr分别为车辆质心到前、后轴的距离；ω为车辆横摆角速度；Fyf和Fyr分别为汽车前后轮的轮胎侧向力；αf和αr分别为车辆前、后轮侧偏角；δf为车辆前轮转向角；β为车辆质心侧偏角.

图1 二自由度车辆模型Fig.1 Two-degree-of-freedom vehicle model

当车辆前轮转向角度不大时，车辆侧向动力学模型可描述为

(1)

式中：m为汽车质量；Iz为车辆横摆转动惯量.

假设轮胎的侧偏特性位于线性范围内，则轮胎侧偏力与侧偏角具有如下近似关系：

Fyf=2kmfαf，Fyr=2kmrαr

(2)

(3)

式中：kmf和kmr分别为车辆前、后轮侧偏刚度.当汽车质心侧向速度较小时，质心侧偏角可表示为β=vy/vx.

把式(2)和(3)代入式(1)，可得：

(4)

AFS控制器的作用是使车辆迅速跟踪理想模型的质心侧偏角以及横摆角速度，将理想二自由度车辆模型所得到的理想质心侧偏角设置为0，理想横摆角速度满足：

(5)

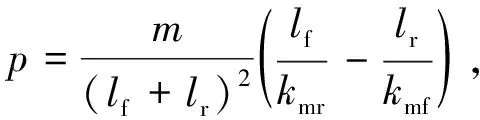
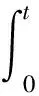
(6)

(7)

1.2 驾驶人模型

本文采用基于单点预瞄的驾驶人模型来进行车辆的路径跟踪，采用传递函数形式，由车辆与期望路径之间的侧向位置偏差来计算的最优方向盘转角为[17]

(8)

式中：Gh为转向比例增益；s为拉氏变换变量；tL为驾驶人微分时间常数；td1和td2分别为驾驶人的纯延迟和肌肉延迟；ΔY(s)为车辆侧向位置偏差，可表示为

ΔY(s)=Ye(s)etps-(Y(s)+vxtpψ(s))

(9)

其中：Ye(s)etps和Y(s)分别为车辆在期望路径预瞄点处和实际的侧向位置；tp为驾驶人预瞄时间；ψ(s)为车辆的横摆角.

2 静态输出反馈控制器的设计

2.1 车辆动力学多胞型模型与问题描述

线性二自由度车辆模型中侧偏刚度为一定值，但车辆在实际行驶中，受路面附着系数、轮胎垂直载荷变化等影响，侧偏刚度具有不确定性.因此，基于饱和线性轮胎模型，对侧偏刚度进行修正[18]：

kf=qfkmf,kr=qrkmr

(10)

式中：kf、kr分别为修正后前、后轮的侧偏刚度；qf、qr为修正系数.

设qf、qr分别在区间[qfmin,qfmax]、[qrmin,qrmax]内变化，则这两个参数可组成4个顶点：

(11)

将式(10)代入式(6)，可得线性时变的系统矩阵和输入控制矩阵为[18]

Φ0+qfΦ1+qrΦ2

(12)

(13)

由式(11)与(12)可得各顶点处的局部状态矩阵为

(14)

取采样时间tsam=0.001 s，采用欧拉方法对各顶点处状态空间的系统模型进行离散化可得[19]

x(k+1)=Ax(k)+B1w(k)+B2u(k)

(15)

(16)

式中：I为单位矩阵.

由式(16)可知，车辆动力学系统模型式(15)实质上是一个多胞型模型，系统矩阵和输入控制矩阵可表示为如下形式[20]：

(17)

考虑到车辆的侧向速度通常需要使用高性能传感器来测量，因此从实际应用出发，采用基于输出反馈的控制方法，选取x2、x3作为系统测量输出变量，则有：

y=C2x+D21w

(18)

(19)

为保证实际横摆角速度能够跟踪理想横摆角速度，并使质心侧偏角的理想值与实际值偏差尽量小，选取横摆角速度与质心侧偏角跟踪误差为系统的控制输出，即

z=C1x+D11w

(20)

(21)

将式(18)和(20)进行离散化处理，结合式(15)，用于设计AFS控制器的车辆侧向动力学模型可表示为

(22)

考虑SOF控制器的设计，其控制律可定义为

u(k)=Ky(k)

(23)

式中：K∈R1×2为控制增益矩阵，R1×2为所有1×2个实矩阵的集合.由式(18)可知，式(23)就相当于比例-积分(PI)控制.

将SOF控制器应用到系统式(22)中，可得以下闭环系统：

(24)

Acl=A+B2KC2,Bcl=B1+B2KD21

(25)

所设计的控制器应使系统在存在参数不确定性时具有鲁棒稳定性，并且保证系统具有良好的动态与稳态性能.设Ezw为系统式(24)中由w到z的闭环传递函数，则控制目标可以表述为：对于一给定的正标量γ，为系统式(22)找到一个合适的控制器式(23), 使得闭环系统式(24)渐近稳定且满足‖Ezw‖∞<γ；同时将闭环系统的所有极点配置在圆心在(-a, 0)，半径为b的圆盘区域N(a,b)内.

2.2 静态输出反馈鲁棒控制器设计

本节设计使系统同时满足极点配置约束与H∞性能约束的SOF控制器，同时需要考虑系统模型参数的不确定性.SOF控制器的设计是一个困难的非凸问题，文献[16]和[21]提出了一种CTM优化方法.

定义Tbj为一坐标转换矩阵，当B2cj为一列满秩阵时，则有：

(26)

以下引理给出了CTM的一个参数化解[15].

引理1当系统控制矩阵B2cj为一列满秩矩阵时，总存在一非奇异矩阵Tbj∈R3×3使得式(26)成立，且有：

(27)

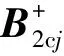
CTM在解决SOF控制问题上起了至关重要的作用，本文将在后续中加以说明.

以下两个引理分别描述了线性时不变系统区域极点配置约束和H∞性能的约束[15, 22].

引理2闭环系统矩阵Acl的所有特征值都落在圆盘N(a,b)内，当且仅当存在一个正定矩阵P∈R3×3与矩阵S∈R3×3，使如下矩阵不等式成立：

(28)

引理3闭环系统(24)是稳定的并且满足‖Ezw‖∞<γ当且仅当存在一个正定矩阵P∈R3×3与矩阵S∈R3×3，使得以下矩阵不等式成立：

(29)

通过适当运用CTM和松弛变量技术，文献[22]提出了同时考虑系统区域极点配置约束和H∞性能约束的LMI充分条件，但并未考虑系统参数的不确定性，因此不能直接用于SOF控制器的设计.为解决这一问题，本文提出如下定理：

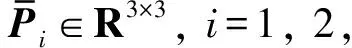
(30)

(31)

j=1, 2, 3, 4

(32)

那么存在一个SOF控制器使得系统(22)稳定且闭环系统式(24)满足‖Ezw‖∞<γ，并且闭环系统矩阵Acl的所有特征值都位于圆盘N(a,b)中.在式(32)中表示的Tbij即为考虑参数不确定性的非奇异坐标转换矩阵，i=1, 2,j=1, 2, 3, 4.而系统的静态输出反馈控制增益矩阵可表示为

(33)

证明由文献[15]的定理1可知，式(31)可变换为如式(29)的形式，即

(34)

j=1, 2, 3, 4

成立，其中：

Aclj=Acj+B2cjKC22,Bclj=B1cj+B2cjKD21

(35)

因此，系统在每个顶点处稳定.由式(16)的定义可得：

(36)

则由文献[20]的定理3.3可知式(34)与式(29)是等价的，即闭环系统式(21)稳定且满足‖Ezw‖∞<γ.类似地，可以证明系统满足区域极点配置要求，篇幅所限在此不再赘述.

由式(32)可知，LMI式(30)、(31)的解受坐标转换矩阵Tbij的选择影响.更具体地说，式(27)所示的矩阵中常数矩阵Tc1j的选择将影响LMI式(30)、(31)的可行性，而非奇异矩阵Tc2j的选择则不会[21].

本文所述的SOF控制器的设计是一个多目标优化问题，其局部最优解可以通过求解以下问题来逼近.

问题1寻找合适的坐标转换矩阵，Tbij(更具体地说，Tc1j)，i=1, 2;j=1, 2, 3, 4, 使以下凸优化问题的解γ最小.

minγ

s.t. LMI (30) 与 (31)

(37)

因此，如何找到一个合适的矩阵Tc1j是SOF控制器设计过程中的关键.基于上述讨论，本文应用文献[23]中提出的NM-HS(Nelder-Mead and Harmony Search)混合算法与文献[22]中提出的CTM迭代优化算法来求解问题1.首先，应用NM-HS混合算法来设计具有极点配置约束的SOF控制器增益矩阵K1，由初始的K1经过计算得到初始的CTM，Tbj；然后扩展并推广运用文献[22]中的算法3，考虑系统不确定性参数的加入，通过对8个常数矩阵Tc1进行迭代更新得到最优的Tbj并同时求解问题1得到γmin以求得局部最优解，再根据式(33)求得对应的SOF控制器.

3 仿真结果及分析

本文应用MATLAB/Simulink和CarSim联合仿真环境对上节所设计的SOF控制器进行仿真验证，仿真工况选择双移线工况和蛇形线工况，联合仿真框图如图2所示.在AFS系统中，本文设计的SOF控制器用来计算图2中的辅助转向角δfc.

图2 联合仿真控制框图Fig.2 Block diagram of co-simulation control

假设期望路径已预先通过路径规划得到.仿真中使用的整车模型选择为CarSim中的E-Class/Sedan，参数如表1所示，轮胎与路面的附着系数设为0.85.为了更好地表现控制器的控制效果，将驾驶人模型选择为非熟练驾驶人，驾驶人特征参数设置为Gh=0.7,td1=0.06 s,td2=0.2 s,tL=0.09 s.由于驾驶人预瞄时间与驾驶人自身、车辆行驶速度和行驶工况等因素有关，所以在进行双移线工况与蛇形线工况仿真中，将预瞄时间分别设置为0.58 s和0.53 s.

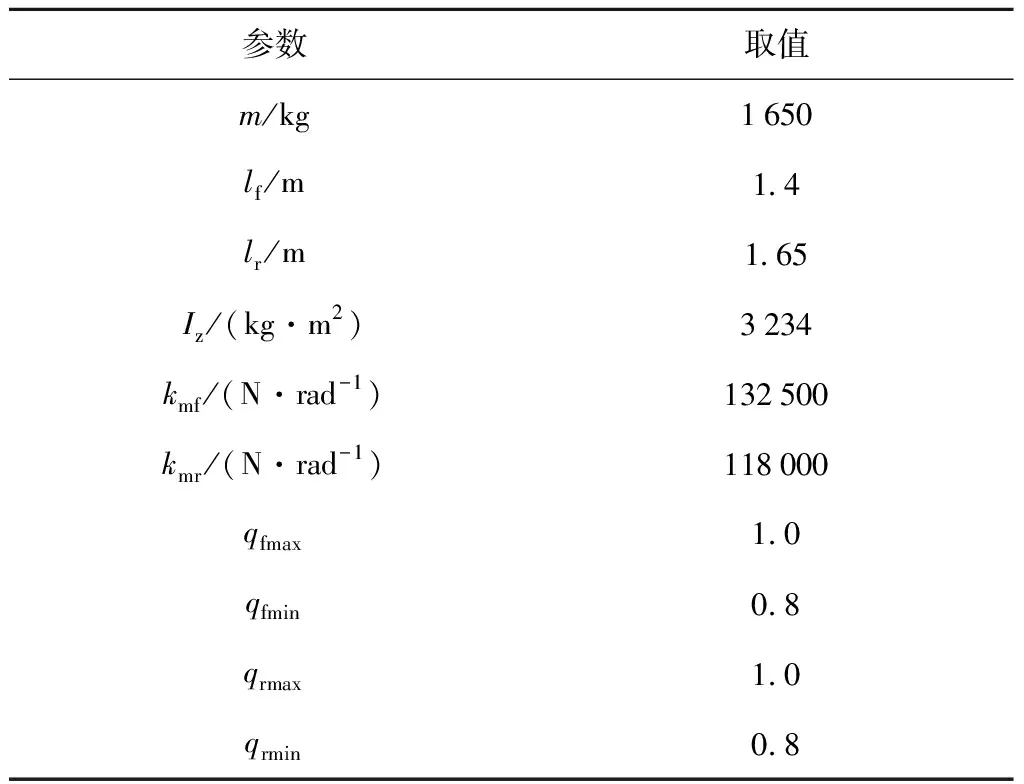
表1 仿真车辆模型参数Tab.1 Simulation vehicle model parameters

3.1 双移线工况仿真

在进行双移线工况仿真时，车速设置为24 m/s，应用NM-HS混合算法以及迭代算法对问题1进行求解，极点配置区域选择为N(0, 0.99)，可求得初始的H∞范数γini=22.510 2，对应的初始SOF控制器增益矩阵Kini=[0.199 75.255 7]，经过CTM迭代优化后的H∞范数的最小值γmin=18.368 6，此时SOF控制器增益矩阵Kopt=[4.698 372.427 4]，仿真结果如图3所示.其中：ωerr为横摆角速度跟踪误差；ay为侧向加速度；δ为车辆转角；X和Y分别为纵向与侧向位移；t为仿真时间.

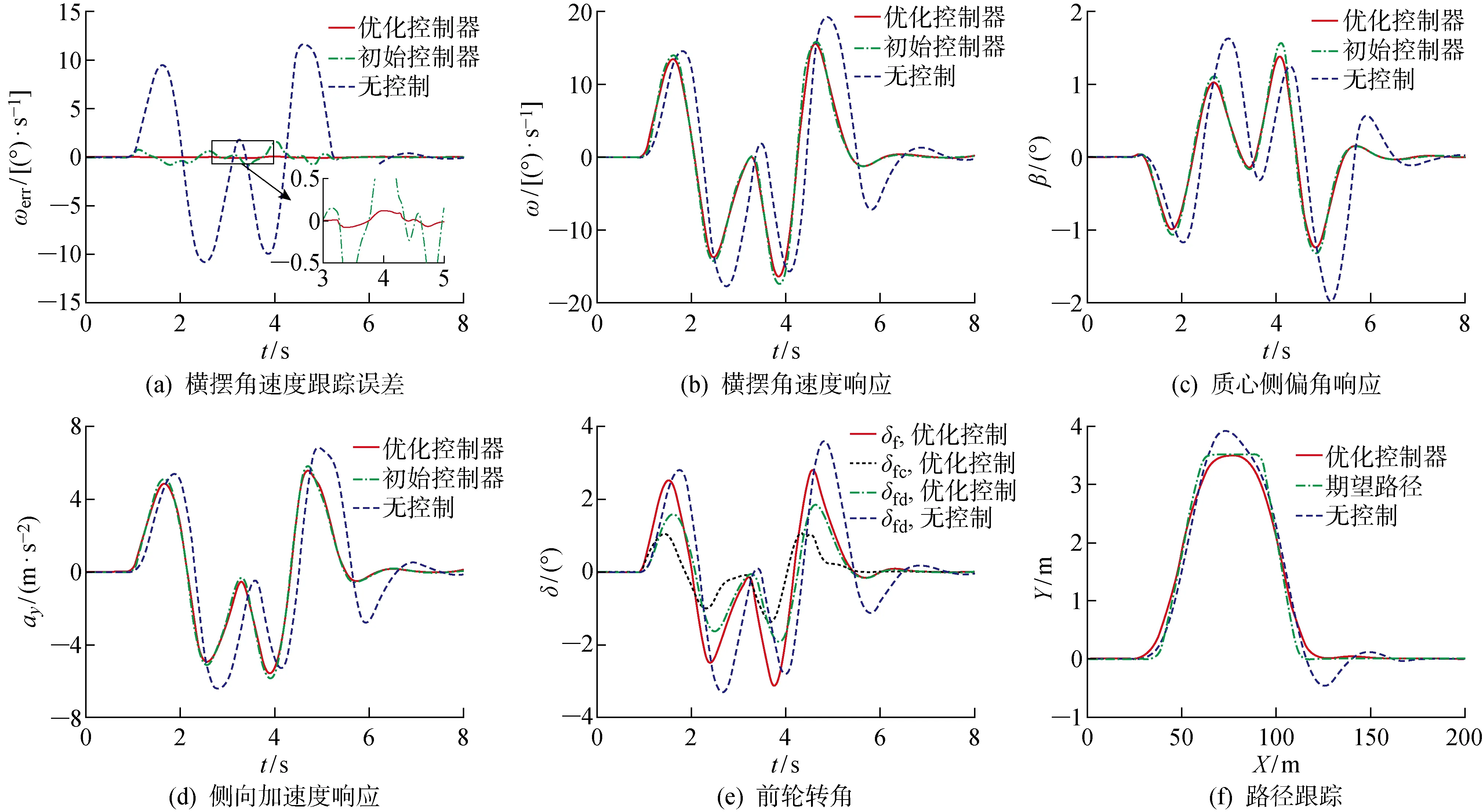
图3 双移线工况仿真对比结果Fig.3 Simulation comparison results under double line shifting conditions

由图3(a)可以看出，经过优化后的SOF控制器可以大幅度地降低车辆横摆角速度的跟踪误差，提高车辆的跟踪性能.通过图3(b)～3(d)可知，与初始控制器相比，优化后的SOF控制器控制效果更好；在优化控制器的作用下，车辆的横摆角速度、质心侧偏角以及侧向加速度均明显减小且快速达到稳态，说明车辆的舒适性与安全性得到提高.同时可以看出，施加控制后车辆的前轮转角、横摆角速度与质心侧偏角响应速度加快，提高了车辆横摆角速度的跟踪性能.由图3(e)和3(f)可知，优化后的控制器加入使前轮产生了一个额外的辅助转角以确保跟踪性能.当不施加控制时，仅依靠所建立的非熟练驾驶人模型虽然也能完成双移线工况试验，但是出现了较大的侧向偏移量，路径跟踪效果不理想.施加控制后，驾驶人可顺利地完成路径跟踪操作，且跟踪误差较小.上述结果表明，所设计的AFS鲁棒控制器可以显著提高车辆的操纵稳定性并改善乘坐舒适性.

3.2 蛇形线工况仿真

在进行蛇形线工况仿真时，车速设置为20 m/s，此时通过求解问题1可求得初始的H∞范数γini=15.145 8，对应的初始SOF控制器增益矩阵Kini=[0.306 19.981 3]，经过CTM迭代优化后可得H∞范数的最小值γmin=12.650 8，SOF控制器增益矩阵Kopt=[5.458 893.699 3]，仿真结果如图4所示.

由图4(a)可以看出，与初始控制器相比，优化后的控制器可进一步降低车辆的横摆角速度跟踪误差.由于在初始控制器作用下车辆的横摆角速度跟踪误差已达到一较小值，所以图4(b)～4(d)中所示的两种控制器的控制效果差别不大.同时由图4(a)和4(e)可知，蛇形线工况下车辆的横摆角速度跟踪误差在由优化后的SOF控制器产生的辅助转角干预下大幅度降低，大大提高了横摆角速度的跟踪性能.图4(d)～4(f)表明了施加控制后车辆的横摆角速度、质心侧偏角以及侧向加速度均有不同程度的减小，说明了车辆的舒适性与稳定性都得到提高.同时由图4可以看出，在优化控制器的作用下车辆的前轮转角、横摆角速度和质心侧偏角的响应速度加快，从而保证了横摆角速度的跟踪性能.由图4(f)可以看出，施加优化控制后车辆路径跟踪误差明显减小，AFS系统可很好地辅助驾驶人完成路径跟踪操作.综上所述，所设计的AFS鲁棒控制器可以很好地跟踪期望的横摆角速度，提高车辆极限工况下的操纵稳定性.

图4 蛇形线工况仿真对比结果Fig.4 Simulation comparison results under serpentine line working conditions

4 结语

本文设计了一种基于SOF的AFS鲁棒控制器，以提高车辆对期望横摆角速度的跟踪性能.为了处理系统侧偏刚度的不确定性，建立了车辆侧向动力学多胞型模型.通过对CTM与松弛变量的应用，提出了考虑系统不确定性的使系统满足极点配置与H∞性能约束的充分条件，并首次将CTM优化方法推广应用到具有不确定性的系统的鲁棒H∞SOF控制器的设计问题，以提高系统的动态与稳态性能并保证良好的鲁棒性.MATLAB/Simulink和CarSim的联合仿真结果表明在双移线和蛇形线等极限工况下SOF控制器能使车辆很好地跟踪理想横摆角速度，显著提高车辆的操纵稳定性并改善乘坐舒适性.在极限工况下车辆轮胎进入非线性区，仿真结果也说明了SOF控制器能使系统保持良好的鲁棒性.