六自由度波浪补偿平台的神经网络自适应反馈线性化控制
2022-03-07王书恒
丁 明, 孟 帅, 王书恒, 夏 玺
(1. 上海交通大学 海洋工程国家重点实验室,上海 200240;2. 中国船舶重工集团公司第七一一研究所,上海 201203)
在海上航行、海洋资源勘探以及货物吊运的过程中,波浪升沉运动会给作业带来许多困难和安全隐患[1],需要波浪补偿设备进行辅助作业.六自由度波浪补偿平台能够进行全自由度补偿,因此效果最佳[2].目前市面上的六自由度波浪补偿平台只有Ampelmann公司生产的Stewart波浪补偿并联机器人.国内在波浪补偿领域的技术并不成熟,其系统控制面临的主要问题是不确定参数和未知干扰[3].大长径比阀控液压系统普遍存在着由电液转换和控制元件的节流特性等因素引起的非线性环节,这使得比例系数-积分系数-微分系数(PID)等传统的线性控制难以满足六自由度波浪补偿平台高精度、大距离及快速响应性的应用场合[4].近年来,反馈线性化、滑模控制等非线性控制的应用大大改善了液压系统的控制效果.赵华等[4]基于反馈线性化设计的二次型最优控制,提高了控制精度和速度.何常玉等[5]设计出能够自适应的鲁棒控制策略,通过对未知参数的精确在线估计,提高了液压控制系统的抗干扰能力.高翔等[6]利用继电器反馈辨识液压系统,并通过Ziegler-Nichols 方法对PID控制器进行自校正,一定程度上克服了液压系统非线性的问题.苗中华等[7]采用指数趋近率的方法设计了滑模变结构控制器,实现了低速下的高精度信号跟踪.已有的研究使得液压系统能够满足浅海区的控制需求,但这些控制方式大都建立在精确数学模型之上,在深海区环境和未知干扰下模型不再准确,此时控制率并不能完全反映系统的真实特性[4].这就需要控制方法的与时俱进,推陈出新.随着智能化时代的到来,智能控制和自适应的思想可以很好地被应用到工业控制中去,其中基于神经网络的反馈线性化可以有效解决非线性对象中模型不确定性、参数扰动及非线性效应等问题[8].近几年,国内外学者已将这类控制方式应用到许多系统中,并取得了理想的控制效果[9-12].本研究尝试利用自适应思想,将其改进并引入到六自由度波浪补偿平台液压系统的控制中,以期提高六自由度波浪补偿平台在深海区的控制精度和抗干扰能力.
首先建立六自由度波浪补偿平台非对称液压系统的非线性模型,然后基于RBFNN辨识,利用反馈线性化设计自适应控制器,最后与经典PID控制和非线性滑动模态控制进行对比仿真分析.
1 液压系统建模
六自由度波浪补偿平台是一种基于Stewart平台的六自由度并联机器人,通过6个液压杆的伸缩耦合出上平台的六自由度运动,能够补偿海浪引起的船舶六自由度响应,可用于对平稳性要求较高的海上作业任务.国内外学者已详细阐述其结构原理及实现方式[13-15],这里不做详细介绍.下面着重介绍液压系统的建模.
大长径比非对称式液压系统的结构如图1所示.图中:p1、p2分别为液压缸左、右腔压强;xv、xp分别为阀芯和活塞杆位移;V10和V20分别为液压缸左、右腔初始容积;A1、A2分别为液压缸左、右腔有效作用面积;ps、p0分别为供油压强及回油压强(p0接近大气压强,因此看作0);mt为活塞杆等效质量;FL为干扰力.

图1 非对称式液压系统的结构原理图Fig.1 Schematic diagram of structure of asymmetric hydraulic system

(1)

(2)

式中:Bp为黏性阻尼系数;βe为有效体积弹性模量;Cip为内泄漏系数;Ce1、Ce2分别为正向、反向外泄漏系数.
反馈线性化需要系统的数学模型连续可微,而式(2)引入的sgn函数在0点间断,不利于反馈线性化的应用,同时不符合液压系统的连续性特征.为解决此问题,本研究引入连续tanh函数代替sgn函数,得到改进后的液压系统非线性数学模型:
(3)
设y=h(x),

2 控制策略
并联机器人是多输入多输出(MIMO)系统,各液压缸运动相互耦合,难以协同控制.本研究参考已有文献,通过反解将上平台位姿解耦成独立的六缸伸缩运动[13],使其成为单输入单输出(SISO)系统,从而对每个缸单独控制.SISO系统的状态方程可表示为[8]

(4)
式中:x(k)∈Rn;y(k)、u(k)∈R;f(*)、h(*)∈C∞;f(*):Rn×R→Rn;h(*):Rn→R.当f(0, 0)=0时,系统的初始状态平衡.f(*)、h(*)未知且为光滑函数,可以通过大量的x(k)、y(k)测量数据对f(*)、h(*)进行反演逼近,以此将式(4)中唯一的未知量u(k)解出,从而得到液压系统的精确控制量,完成系统的控制工作.已有的研究证实这种方式具有相当的可靠性[17-21].
2.1 系统辨识
在系统平衡状态的某一邻域Φ内,可以用自回归滑动平均模型(NARMA)来表示式(4)中SISO系统[21]:
y(k+d)=F(y(k),y(k-1), …,y(k-n+1),
u(k),u(k-1), …,u(k-n+1))
(5)

u(k)=G(y(k),y(k-1), …,y(k-n+1),
y′(k+d),u(k-1), …,u(k-n+1))
(6)
这里连续函数G(*):Rn→R.则u(k)的求解就变成根据输入输出信号的观测值估计映射G(*).G(*)可以用神经网络进行逼近,但由于计算量大,运算缓慢,不能对系统有效实时控制[17],故需要对式(6)进行改进.将NARMA模型在邻域内平衡点进行泰勒展开,便可导出改进自回归滑动平均模型(NARMA_L2)方程[17]:
y(k+d)=f0(Y,U)+g0(Y,U)u(k)
(7)
Y=y(k),y(k-1), …,y(k-n+1)
U=u(k-1), …,u(k-n+1)
式中:(Y,U)∈RY×RU,RY×RU是Rn×Rn的有界紧集.由于连续函数在紧集中有界,故只要能够合适取RU,就能够使NARMA_L2方程足够精确[17].需要用两个神经网络辨识模型N1、N2分别辨识f0(*)、h0(*).宋学伟等[12]已证实了RBFNN高精度快速收敛的优势,因此本研究引入RBFNN对f0(*)、h0(*)进行辨识,得到神经网络辨识模型:
(8)


图2 RBFNNNARMA_L2辨识模型Fig.2 Identification model of RBFNN NARMA_L2
2.2 控制器设计
由本文1.2节得知n=3,故取d=2.利用RBFNN辨识系统的动态特性,得到六自由度波浪补偿平台非对称液压系统的NARMA_L2模型:

通过现场聆听讲解和结合高科技电子技术模拟再现情景体验,大家接受了一次深刻的红色教育,党性得到进一步锤炼,思想得到进一步洗礼。广大党员干部纷纷表示,要坚定理想信念,继承和发扬革命先辈坚忍不拔、顽强拼搏、勇往直前的大无畏精神,一定要倍加珍惜今天的美好生活,时刻牢记全心全意为人民服务的宗旨,继续发扬艰苦奋斗的精神,以实际行动做一名合格的共产党员。深入学习贯彻党的十九大精神、习近平总书记系列重要讲话,不忘初心、尽职尽责、尽力而为,用实践诠释担当,在担当中锤炼党性,为德州生态文明建设贡献力量。
y(k-1),y(k-2),u(k),u(k-1),
u(k-2))u(k+1)
(9)

(10)
式中:y′(k+2)为系统期望输出.
2.3 在线修正


(11)

(12)
用sgn{g0(T)}代替式(12)中g0(T),得到最终的在线修正公式:
(13)
自适应控制系统的框图如图3所示.

图3 RBFNN反馈线性化自适应控制系统框图Fig.3 Block diagram of RBFNN feedback linearized adaptive control system
3 仿真与对比
3.1 阶跃干扰仿真
液压系统的参数取值如表1所示.取步长为0.001 s,对液压系统施加阶跃信号并进行跟踪,在t=3 s时加入随机干扰力,3种控制方式跟随曲线和误差如图4所示,图中:Des为位移;Err为跟踪误差;t为时间.可以发现,阶跃干扰下相比于传统的PID控制和滑模控制,新型控制方式几乎没有超调现象,三者的相对误差分别为2.9%、1.1%及0.3%.由于新型控制方式能够根据误差自适应调节参数,收到外界干扰后能够更快更高精度地跟踪信号,故相对误差要明显低于其他控制方式.新型控制方式稳性强,在超调方面以及抵抗干扰和信号跟踪上展现出一定的优势,为波浪补偿装备的安全运行提供了保障.

表1 非对称液压系统参数Tab.1 Parameters of asymmetric hydraulic system

图4 阶跃干扰信号跟随和误差曲线Fig.4 Curves of step interference signal tracking and error
3.2 五级海浪干扰仿真
根据已有研究,海浪可利用海浪谱进行反演.本研究选取国际拖曳水池会议(ITTC)双参谱进行波普模拟,海浪等级为五级、有义波高h1/3=2 m、特征周期T1=8 s,与全国水动力学研讨会所展示的海浪谱[22]相吻合.利用海浪谱反演出海浪波形曲线,如图5所示.

图5 五级海浪波形曲线Fig.5 Wave curve of five-level wave
船体对波浪的响应可以解耦为6个自由度,分别为横摇、纵摇、艏摇、纵荡、横荡及垂荡,如图6所示.海浪对船舶运动状态的影响主要转化为海浪等级以及海浪与船舶之间的攻击角两方面因素.海浪传播方向与船舶航向所成夹角被称为遭遇角,用χ表示.任意自由度响应(Res)可通过幅值响应算子(RAO)、海浪谱及海浪正弦波功率代入到海浪响应正弦波形公式并将其各个频率相互叠加来求得[23]:

图6 船体的六自由度和遭遇角Fig.6 6-DOF and angle of encounter of hull
(14)
式中:Rζ为海浪干扰作用下船舶对于海浪的幅频响应算子;ωi为第i个分波的海浪频率;S为船速;σ2(ω1, i,ω2, i)为第i个分波的功率;ωe, i为第i个分波的频率;φi为第i个分波的初相位.
船舶在90° 遭遇角下的艏摇和横荡最大,船舶的海浪响应也最剧烈,因此对这种工况下船舶的海浪响应进行仿真研究.RAO数据来源于中国船舶及海洋工程设计研究院对S-175型集装箱船的船模实验.根据实验数据,对频率位于[0.2, 2] rad/s的19个分波(n=19)进行计算,通过式(14)转换为船体对海浪的六自由度响应,如图7所示,图中θ为3个旋转自由度的角度.

图7 船体在五级海浪下90° 遭遇角时的海浪响应Fig.7 Wave response at 90° angle of encounter and level 5 waves of hull
根据船体的六自由度响应,可对波浪补偿平台进行运动学反解,通过计算得到液压杆伸缩量的解析解.取步长为0.001 s,将反解得到的曲线作为液压系统的跟踪信号,并施加干扰,跟踪曲线和误差如图8所示.在五级海浪及干扰下,PID控制的最大误差达到了87.2 mm,平均误差36.5 mm,精度低,动态性能十分差.滑动模态控制的平均误差为11.8 mm,有很大提升,且具有一定的抗干扰能力.而本文提出的控制策略平均误差只有2.3 mm,是3种控制方式中唯一将跟随误差能够保持在10-3m级别的控制方式.由此可知,在五级海浪以及外力干扰下,大长径比液压系统参数变化大、补偿距离长、速度快,动态性能相对较差的PID无法及时控制,虽然滑模控制的跟踪速度快,误差也比较小,但在幅值接近3 m的补偿中还是无法做到迅速高精度跟随.新型控制方式的系统辨识精确度高、控制率精准且能够自适应参数变化,因此能够紧贴期望信号,无论是跟踪速度还是精度都大大提高,能够实现速度快、跨度大的信号跟踪,满足六自由度并联平台在深海区海浪补偿任务要求.
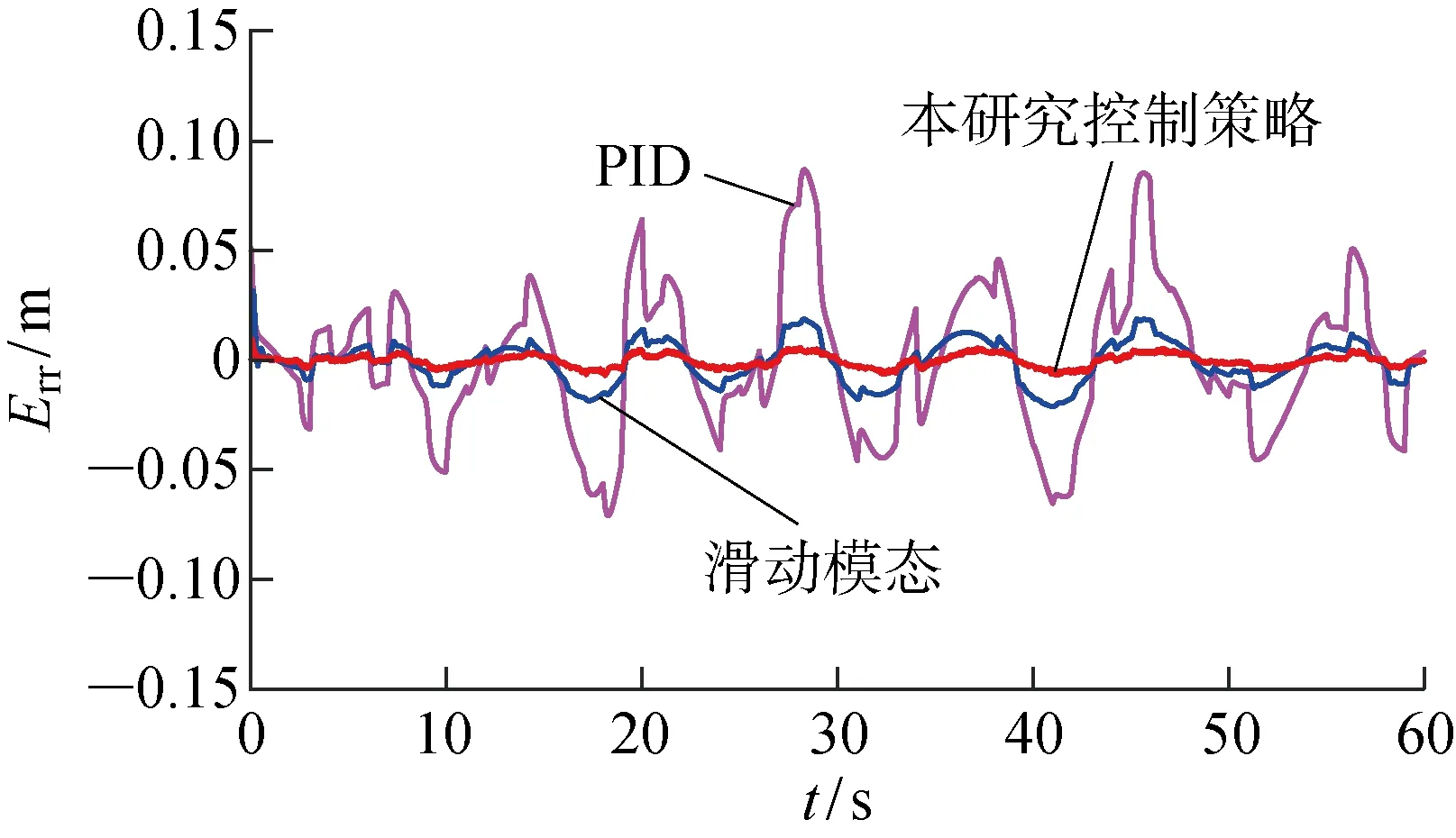
图8 五级海浪信号跟踪误差曲线Fig.8 Curves of signal tracking error of level 5 wave
4 结语
以深海区工况下六自由度并联平台所采用的大长径比液压系统为研究对象,在有关对液压系统控制领域研究的基础上,针对性地提出了基于RBFNN辨识的自适应反馈线性化控制策略,以改善大长径比液压系统在深海区海洋环境下伸缩量大、速度快及难以跟踪的问题.以S-175型集装箱船为算例,利用MATLAB/Simulink,在船舶受到90°遭遇角的五级海浪作用和阶跃干扰下开展仿真分析,证实了新型控制策略在深海区高速大跨度的波浪补偿任务和恶劣海浪环境的干扰下,依旧可以保持良好的控制精度和较强的稳健性,可为六自由度波浪补偿平台控制系统设计提供参考.
虽然提出的控制策略实现了抗干扰、低误差和快速跟踪,在仿真中满足六自由度波浪补偿平台液压系统的控制需求,但在控制过程中会出现跟踪轨迹在期望值附近来回抖动的现象.需通过不断的参数调整以及对神经网络进行训练,抖振方可控制在可接受的运行范围内,但依然无法完全消除,离线辨识也不利于工程应用.在未来的研究工作中,将尝试改进控制策略,深入探究抖振机理并尝试实现系统整体在线辨识和六缸协同控制,以改善控制效果.
