怎样用数形结合思想和整体代换思想解答解三角形问题
2022-03-06刘兵
刘兵
解三角形问题通常要求根据已知的三角形边角关系、图形,求三角形的角的大小、边长、周长、面积、中线的长、高线的长等.此类问题看似较为简单,但解题过程中的运算量较大,极易出现运算错误.经研究,笔者发现在解题时,巧妙运用数形结合思想和整体代换思想,可有效规避运算错误.
一、借助数形结合思想
若遇到一些与三角形边角关系有关的问题,可根据题意画出相应的图形,并添加适当的辅助線,将“数”“形”结合起来,利用几何图形的位置关系和性质来分析问题,就能快速求得问题的答案.
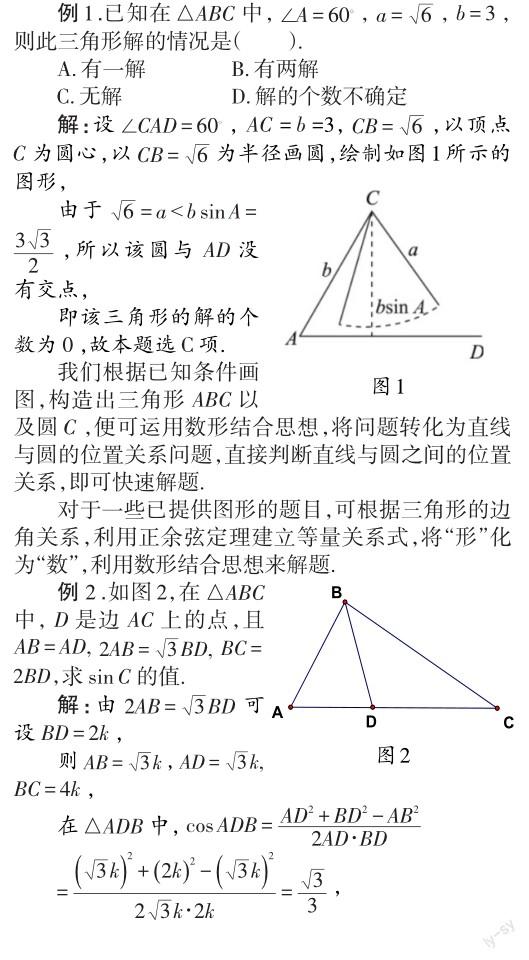

解答本题主要运用了数形结合思想.先根据图形以及△ABD的三边比例,利用余弦定理建立关系式,求出∠BDA;然后根据补角关系求出∠BDC;再在△BDC中,利用正弦定理求出sinC的值.
二、运用整体代换思想
整体代换思想是指根据所求式子的结构特征,将某些含有未知量的式子当作一个整体,进行代换,从而求得问题的答案.整体代换思想常用于解答解三角形问题中的运算问题.在解题时,需建立已知条件与所求目标式之间的联系,选择合适的式子或其中一部分进行等量代换,从而简化运算.
例3.已知△ABC的内角A,B,C的对边分别为a,b,c,若bsinC+csinB=4asinBsinC,b2+c2-a2=8,求△ABC的面积.
解:因为bsinC+csinB=4asinBsinC,
所以由正弦定理可得sinBsinC+sinCsinB= 4sinAsinBsinC .
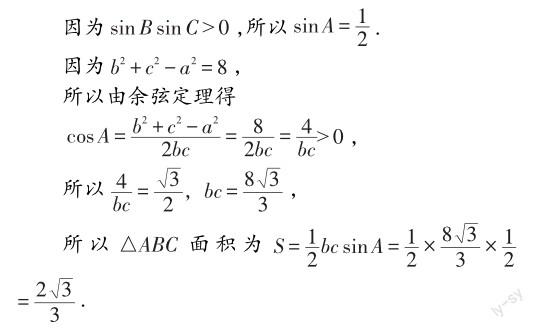
解答本题,需灵活运用正弦定理和余弦定理求得bc的值,然后将其看作一个整体,代入三角形的面积公式中,利用整体代换思想求得△ABC的面积.
总之,在解答解三角形问题时,灵活运用数形结合思想、整体代换思想,能有效地简化运算,提升解题的效率.同学们在解题的过程中,要学会根据题目的特点、已知的三角形边角关系和图形来选用合适的方法求解.
(作者单位:江苏省如东县马塘中学)
