增强四种意识，提高解题效率

张玉敏

解答数学问题，需要具备想象、观察、判断、分析、推理、运算等能力.而要有效地提升解题的效率，除了要掌握并运用基本的数学知识、方法外，还需增强联想意识、目标意识、优化解题方法的意识、反思意识这四种意识.

一、联想意识

审题是解题的第一步，也是解题的关键.那么，怎样才能审好题呢？我认为可尝试联想，即逐一分析题目的式子、图形、条件、结论，根据其形式、结构、特点联想到所学的公式、定理、性质、法则等，也可将问题与以前遇到的类似题目、解题方法相关联，通过类比、延伸，找到两个题目之间的联系，从而寻找到解题的方案.

数与形是数学中不可分割的两个部分，二者之间可以相互转化，通过联想，由“数”思“形”，进而构造出几何图形，利用几何图形的性质、位置关系，就能快速解题.

二、目标意识

解题是一种有目的的行为.解题时，需有目标意识，解题的每一步都是为了求得问题的答案，一旦失去方向，就很难达到目标.在解题时，需首先明确目标，即所要求得的式子、数值、范围以及所要求证的结论，这样才不会偏离正确的解题轨道.解题的每一步都要做到有理有据，且要明白进行这一步的目的是什么，这样才能明确下一步该做什么，如，建立关系式的目的是为了化简目标式；列方程的目的是为了应用韦达定理.

例2.已知P、Q是f（x）=x2+ax+b（-1≤x≤1）上两个不同的点，且满足f（0）=f（1）=0.

（1）求实数a，b的值；

（2）求直線PQ的斜率的取值范围；

三、优化解题方法的意识

解题须讲究方法，有了好的方法，则会事半功倍.若解题的方法选择不当，则会导致解题过程太繁琐，或者无法得到正确的答案.在解题时，同学们需仔细审题，将已知条件和所求目标关联起来，寻找不同的解题方法，如设而不求、整体代换、数形结合等，然后将各种方法进行比较，选取最优的方案，这样有利于提升解题的效率.

例3.已知圆C的方程为（x-1）2+（y-2）2=25，直线l的方程为（2m+1）x+（m+1）y-7m-4=0（m∈R）.求证：不论实数m取何值，直线l总与圆C相交.

解析：若采用常规方法，利用方程思想，需将圆C的方程与直线l的方程联立，然后消元，得到一元二次方程，最后验证该方程的判别式是否恒大于0.但运用该方法求证，计算量颇大，且容易出错.这时，我们要有优化解题方法的意识，寻找更为简便、有效的方法进行求解.对于含有参数的直线方程，应关注它是否经过某个定点，仔细研究直线l的方程，可发现这个定点在圆C内，那么结论就不言自明了.

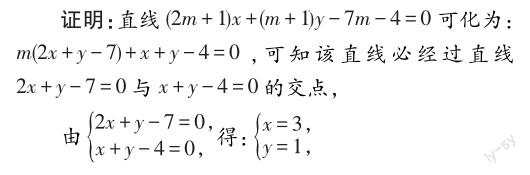
则两直线的交点为A（3，1），

而此点在圆的内部，故不论m为任何实数，直线l与圆C始终相交.

显然，这种证法要简捷多了，不仅运算量小，而且思路简单，这样可以节约大量的时间.

四、反思意识

解题完成后，能否保证得到的结果是正确的呢？能否保证这种解法是最好的解法呢？这时，我们就要有反思意识，通过反思，完善解题的过程，确保解题成功.那么，该反思什么呢？我认为可以从以下几个方面入手：（1）反思答案的合理性；（2）反思解题过程的严谨性；（3）反思解题过程中的易错点；（4）反思解题过程中用到了哪些思想方法；（5）反思能否从本题出发，得出相关的结论.通过反思，可以得到更多新的体会和收获.

故所求直线的方程为y-3=±（x-1），即x-y+2=0或x+y-4=0.

在解答本题后，我们可以从两个方面进行反思：一是重新审题.一般地，直线与抛物线有一个交点，则会出现两种情形：（1）直线与抛物线相交于一点；（2）直线与抛物线相切.那么在该解法中，忽略了直线与抛物线相切的情形，因此上述解法中漏了一解：x=1；二是检验所得的结果是否满足题意.

在解题时，同学们要根据题目进行联想，确定每一步的目标，选择最优的解题方法，在解题后进行反思，有了联想意识、目标意识、优化意识、反思意识，才能有效地提升解题的效率.

（作者单位：江苏省常州市戚墅堰高级中学）