GNSS天线相位中心偏差标定方法研究

沙文东，程会平，郭昱铭

(武汉市勘察设计有限公司，湖北 武汉 430022)

1 引 言

GNSS定位精度主要受站星间各种测量误差的影响，如电离层和对流层延迟误差、接收机和卫星钟差、多路径误差和天线相位中心误差等。天线相位中心误差主要由于天线的电气中心和几何中心不一致导致的，并与入射信号的强度和角度(方位角、高度角)有关。天线相位中心误差属于观测中的系统误差，天线相位中心偏差(PCO)量级为几厘米至十几厘米。当基线较长或采用非差定位时，相位中心变化误差很难通过差分方法减弱或消除[1]。所以，对于高精度地壳形变测量、精密工程测量等高精度GNSS定位，特别是采用BDS进行高精度定位时，就需要对没有给出相位中心参数的天线进行标定，建立一种天线相位中心误差标定方法显得尤为重要，有重要的应用价值。本文主要研究讨论天线相位中心偏差(PCO)的标定方法。

2 GNSS接收机天线相位中心偏差(PCO)

为了对天线相位中心进行完整的描述，需要引入瞬时相位中心、相位中心变化(PCV)、平均相位中心、相位中心偏移(PCO)、和天线几何中心(ARP)这5个参量。如图1所示[2，3]。天线几何中心一般定义为天线上表面的中心点ARP，即天线的垂直对称轴与天线下地面的交点，平均相位中心的含义为：在整个天线波束空间内，远场的实际等相面用一个理想的等相球面来拟合，若拟合残差的平方和最小，则拟合球面的球心即为平均相位中心。平均相位中心与天线几何中心(ARP)的偏移量称为相位中心的偏移(PCO)，瞬时相位中心与平均相位中心的偏移称为相位中心的变化(PCV)。

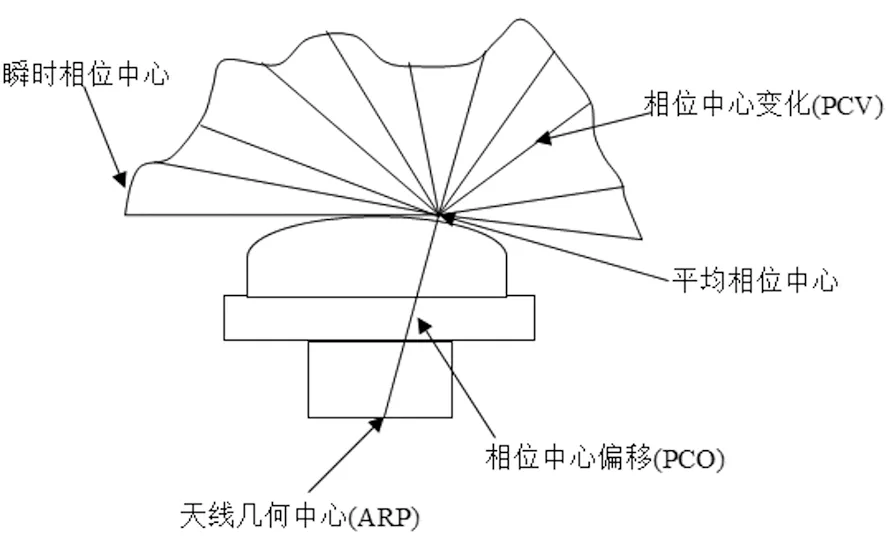
图1 天线相位中心误差示意图

不同类型天线的天线相位中心偏差(PCO)各不相同，相同类型的天线相位中心偏差(PCO)差别极小，一般认为相同。天线相位中心偏差(PCO)还与接收信号的频率有关，不同的频率对应于不同的天线相位中心偏差(PCO)。

经过IGS组织标定的天线相位中心偏移(PCO)值可以从IGS组织发布的天线相位中心改正文件中提取获得。以接收机天线TRM59800为例，其在天线相位中心改正文件中的PCO改正信息如表1所示。

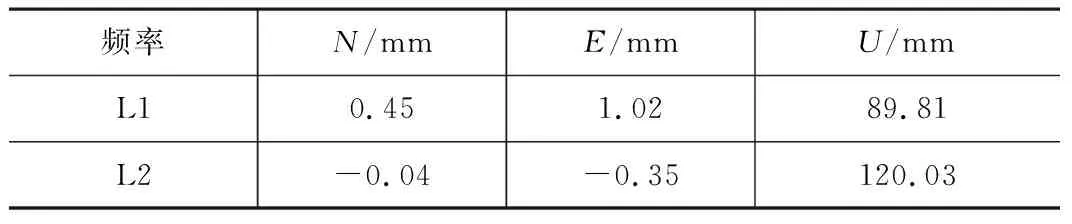
天线TRM59800的PCO标准值 表1

表1显示，对于不同的频率L1和L2，天线相位中心偏差不同，但在水平方向上偏差都在亚毫米级，垂直方向上偏差较大，可达 10 cm左右。

3 GNSS接收机天线相位中心偏差(PCO)对基线解算精度的影响

在GNSS精密定位中，主要采用差分定位，通过短基线测量，采用国际公认的GNSS高精度定位、定轨软件-Bernese软件对数据进行双差处理，解算出测站的全球坐标(X，Y，Z)，为了便于与IGS发布的天线相位中心偏差进行对比，需进行坐标系统转换，转换到站心地平坐标系(N，E，U)。

3.1 WGS-84和站心地平坐标系的转换

GPS测量的坐标系是WGS-84，属于地心坐标系，设GPS基站的WGS84坐标为(X，Y，Z)，基线矢量为(△X，△Y，△Z)，移动站的站心地平坐标(N，E，U)计算步骤如下：

首先计算基站的大地坐标，空间直角坐标系与大地坐标系(B，L，H)的关系是

(1)

式中，N为卯酉圈曲率半径：

(2)

e为椭圆偏心率：

(3)

站心地平坐标系与基线矢量的转换关系为：

(4)

其中，转换矩阵R为：

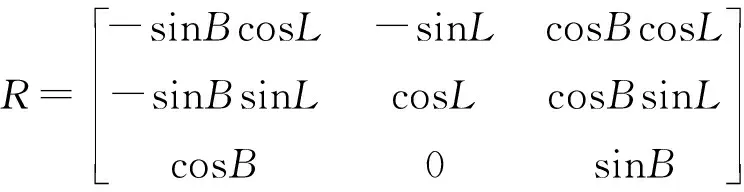
(5)

3.2 天线相位中心误差对基线解算精度的影响分析

实验选用了两个距离大约为4 m的固定桩，在短基线两端分别安置天线进行观测，共做了两组实验，参考站安置TRM59800型号的天线，固定不动，测试站分别安置TRM59800和TRM59900型号的天线，每组实验测量4个测回。利用Bernese软件进行基线解算，截止高度角选为15°。本实验设计了三种方案用来比较天线相位中心偏差对基线解算精度的影响，设计方案[4]如下：

方案一：参考站和测试站的天线相位中心偏差用标准值作改正，作为已知标准基线；

方案二：参考站天线相位中心偏差用标准值改正，测试站的天线相位中心偏差不做改正。

通过方案对比，分析天线相位中心偏差对基线解算精度的影响，如表2、表3所示。

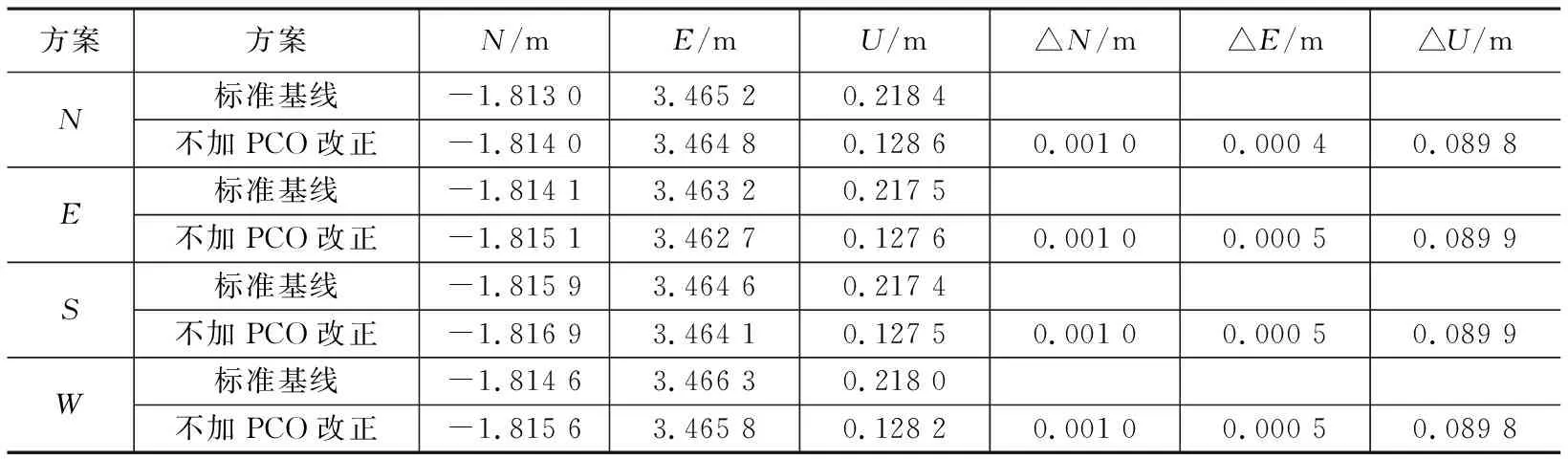
不同的天线相位中心改正方案对基线解算的影响(TRM59800) 表2

不同的天线相位中心改正方案对基线解算的影响(TRM59900) 表3

表2、表3中，基线分量分别与已知标准基线作对比，天线相位中心偏差(PCO)严重影响着基线解算的精度，影响精度达到厘米级；在水平方向上，PCO对基线解算精度的影响都较小，而垂直方向上，影响较大。因此，在GNSS高精度定位中，必须对天线相位中心偏差予以改正。

4 GNSS天线相位中心校正基本原理和方法

GNSS接收机天线相位中心的偏差，可以通过仿真计算，也可采用室内微波测量，还有在室外通过接收GPS信号来标定。目前，仿真计算方法难以精确标定，天线电气相位中心的确定精度有待于进一步验证，而微波暗室测量的设备比较复杂，而且比较昂贵，不适应于普通测绘单位，国内一般的检测部门没有这种检测条件。因此，我们可以采用室外测量，精度也可达到毫米级。目前，天线相位中心偏差的室外测量方法主要有旋转测量法、天线交换法等。在不考虑天线相位中心变化的情况下，下面主要介绍旋转测量法[5，6]、天线交换法[7～9]。

(1)旋转测量法

旋转测量法是一种室外短基线测量方法，这种方法是指假设天线存在N、E(x，y)方向的偏差，在天线旋转的过程中，PCO会引起基线长短的变化，通过解算基线的长度就可以解算出PCO的NE分量，测量原理如图2所示。

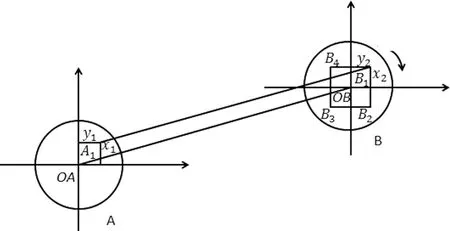
图2 旋转测量法示意图

旋转测量法的实施方案是：

将两个天线分别安置在短基线的两端，并进行水平调整和对准，两天线均指向北方向，观测一个时段(2h)，得到第一时段基线矢量，A天线固定指向北方向，B天线依次顺时针旋转90°、180°、270°，得到第二时段、第三时段、第四时段基线矢量；然后固定B天线指北，A天线依次顺时针旋转90°、180°、270°，得到第五时段、第六时段、第七时段基线矢量。设第i时段所观测的天线之间的基线矢量为(△xi，△yi)，两个天线几何中心(ARP)之间的矢量为(x0，y0)，A天线相对于其天线几何中心的相位中心偏差为(x1，y1)，B天线相对于其天线几何中心的相位中心偏差为(x2，y2)。假定在水平方向上，天线相位中心偏差的影响是相同的，则有如表4中的几个关系式。

坐标差关系式 表4

其中，观测量为基线矢量(△xi，△yi)，i=1，2，3，4，5，6，7，未知量为x0，y0，x1，y1，x2，y2，共有14个观测量、6个未知数。可获得如下形式矢量观测方程为

V=AX-B

(6)

其中，A为系数矩阵，如表4，X为未知相位中心偏差(PCO)的三维坐标矢量，B为观测得到的地面上两天线之间的基线矢量，V为计算得到的基线与观测得到的基线的残差矢量，假设这7个时段的观测为等精度观测，由最小二乘原理，未知数的解为：

X=(ATA)-1(ATB)

(7)

由此可以解算出真实基线(x0，y0)和两个天线的PCO值：(x1，y1)；(x2，y2)。

因为天线在水平面上的旋转并不会引起被测基线在高程分量上的变化，所以计算的结果在垂直方向上为零，故旋转观测法只能用于估算PCO的水平分量。

(2)交换天线法

交换天线法用于标定相位中心偏差(PCO)的垂直分量，也属于短基线测量方法，在相距几米的两个测站上分别安置一台GPS接收机，如图3所示。先进行第一时段( 2 h以内)的相对定位后，再将两台接收机天线互换位置，进行第二时段观测，构成第一测回。

设天线A和B的相位中心在垂直方向上的偏差分别为δhA和δhB，测站A、B的大地高分别为HA和HB，天线高分别为hA和hB，第一时段GPS基线解算的高差(观测值)可表示为：

①增加了电子公交站牌个性化语音播报功能，提升了广告运营灵活度和便捷度；②在公交车上，除了GPS定位，还应采集乘客状况信息（空载、满载等）并在电子公交站牌上显示（用颜色区别），并增加视频监控、人流分析和超速报警等功能。

△H1=(HB+δhB+hB)-(HA+δhA+hA)

(8)

第二时段高差观测值为

△H2=(HB+δhA+hB)-(HA+δhB+hA)

(9)

则两个天线相位中心U方向的偏差之差可以表示为：

(10)

为了获得更高的标定精度，可以进行多个测回观测，最后取平均值作为最终结果。天线交换法测量结果为两个天线在垂直方向的相对偏差。

图3 交换天线法示意图

旋转天线法可以标定天线相位中心偏差的水平方向上的NE两个分量，而且是以绝对偏差的形式给出的。交换天线法主要用于标定天线相位中心偏差的垂直分量，仅能获得两个天线的相对垂直偏差。对于双频接收机，由于L1和L2载波的相位中心是不一致的，因此，必须单独解算L1和L2载波的天线相位中心偏差。

5 GNSS天线相位中心的室外标定方法与实验结果

借鉴国内外研究GNSS天线相位中心偏差的标定方法，本文设计了一种GNSS天线相位中心的室外相对标定方法，利用已知天线的PCO作为参考天线，通过短基线精密测量获得待测天线的相位中心偏差值。

5.1 方案设计

(1)选择一个天线测试场地，视野开阔，地势平坦，建立两个相距较近的固定观测墩(A、B)，并采用强制归心装置，避免天线安装误差，如图4所示。

图4 天线测试场地

(2)选择一个已知天线相位中心偏差(PCO)的天线作为参考天线，并安装在观测墩A上，待测天线安装在观测墩B上。通过段基线相对测量解算待测天线的相位中心。

(3)实验设备包括：两台相同类型的接收机(Trimble R9)，两个相同类型的天线(Trimble59800)。

(4)采用高精度的Bernese软件作为基线解算软件，将实验标定的天线相位中心偏差和变化值与最新的IGS_08天线相位中心改正文件中的标准值进行对比。

(5)将标定的天线相位中心变化值按规定的格式写入IGS_08天线相位中心改正文件中，带入Bernese软件进行基线解算，通过对比分析，检验其精度。

5.2 室外天线相位中心偏差(PCO)的标定方法

(1)实验步骤

根据实验准备条件，采用多方向旋转自主检定，最后用最小二乘法计算天线的相位中心偏差。室外观测时，接收机设置截止高度角取为5°。

具体步骤：

①在A、B两点同时使用Trimble 59800天线，天线均指北，观测三个时段，每一个时段的观测时间不低于 12 h，AB站在基线解算时考虑PCO，获得AB两点的基线分量，并作为标准基线。

②在A点，安置天线Trimble 59800并固定不动，B点安置被测天线Timble 59800并旋转天线，分别指向北(N)、东(E)、南(S)、西(W)4个方向，每个方向观测一个时段，每个时段的时间不低于 1.5 h。基线解算时，仅考虑基站A的天线相位中心PCO。

(2)标定原理

基线处理采用Bernese软件进行基线解算，卫星高度截止角取为15°，基线结果以A点为原点，按站心地平坐标系形式给出，表5为标准基线观测结果，表6为标定测量过程获得的四个方向基线观测结果。在进行处理标准基线时，点A和点B的天线都加入了天线相位中心偏差标准值改正。在标定点B的天线时，A点的天线加入了天线相位中心偏差标准值改正，B点的天线不加天线相位中心偏差改正，作为未知天线处理。

U方向偏差：

垂直方向的相位中心偏差由各个方向的平均值减去标准值获得。

N、E方向偏差：

设：N、E方向的相位中心偏差为εN、εE，基线矢量观测值为(△N、△E、△U)，基线矢量标准值为(dN、dE、dU)，则有如下的关系式：

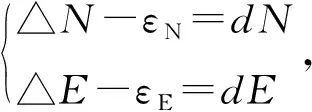
据以上公式，通过计算平均值和均方差可获得天线在水平方向的相位中心偏差及标准差，结果如表7所示。

标准天线观测基线矢量 表5

测试天线观测基线矢量 表6

天线相位中心偏差标定值与IGS_08模型PCO标准值 表7

为了验证本方法的正确性，将标定结果与IGS_08发布的天线相位中心偏差(PCO)标准值进行了对比，如表7所示，该方法标定的天线相位中心偏差值非常接近IGS_08的标准值，说明该方法可靠性较高。

天线相位中心偏差PCO的室外相对测量标定误差取决于基线的观测精度，基线处理获得的双差观测值残差反应载波相位的观测精度，天线的相位残差如图5所示。

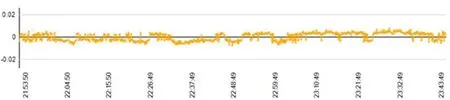
图5 L1双差残差图，相位RMS=0.002 0 m

被测试天线经过L1双差处理，观测精度为0.002 0 m。天线相位中心在水平方向无明显的系统偏差。

借鉴国内外天线相位中心偏差和变化标定方法，利用已知绝对相位中心偏差和相位变化的天线作为参考基准天线，采用相对定位标定方法，获得待测天线的绝对相位中心利用标定的天线PCO值进行基线解算，基线三分量解算精度达到 1.5 mm以内，满足了高精度GNSS解算的要求。

6 结 语

本文通过研究国内外GNSS天线相位中心偏差的标定方法，在此基础上，建立了一种GNSS天线相位中心偏差标定方法，根据精度评定结果分析，这种标定方法是可行的，能极大地提高定位精度。为工程应用的GNSS天线相位中心偏差的校正提供可靠的标定方法。

建议：实际工程应用中，尤其精密工程测量中，必须要考虑天线相位中心偏差(PCO)对定位精度的影响，尤其垂直方向上，影响较大，精度达到厘米级。