2020泰国数学奥林匹克不等式的推广

重庆三峡学院数学与统计学院 (404000) 罗 建 谭安利 古玲玲

题目(2020泰国数学奥林匹克不等式) 已知a,b,c∈R+,a+b+c=3，求证：

文[1]对(1)的证明方法，变式及推广做了探究，将(1)推广为：

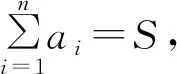
本文拟对推广1作进一步的推广，得到：

显然，上述推广，前四个均是最后一个的特例，因此下面只给出推广5的证明.为了证明推广5,引用文[2]中的不等式5，即：

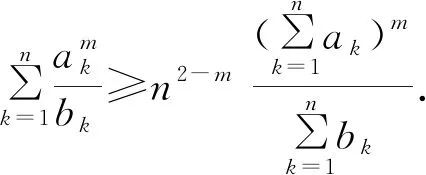
在推广5中,若对其参数赋值，可得许多不等式.例如令λ=2,μ=3,m=3,n=3,S=3，及k=3，l=4就有不等式：

如令λ=1,μ=3,m=2,n=3,S=3，及k=1，l=4就有不等式：