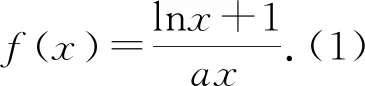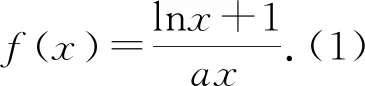一道多参不等式证明方法探究

福建省泉州市第七中学 (362000) 杜成北 陈景文

众所周知，利用导数研究不等式和函数零点一直以来是高考命题热点，常常以压轴题的形式出现.而将两个问题结合在一起考查更是备受青睐，本文以泉州市2022届高中毕业班质量检测一第22题为例，谈谈这类问题的一般性处理方法，希望对读者有帮助.

1 题目呈现

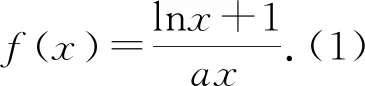
2 题目探源

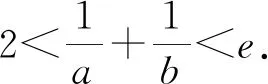
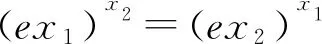
3 解法探析

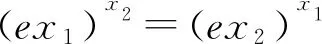
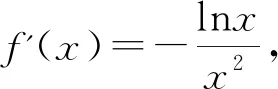
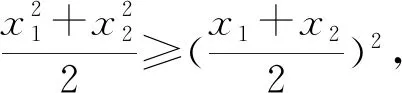
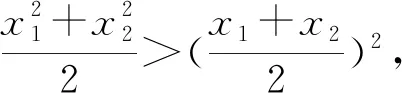
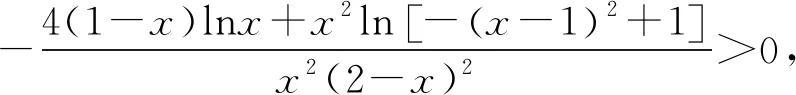
这两种证明方法归纳起来就是均值放缩，对称构造来实现.其实从另一个角度出发，这两种方法都是将多个变量归一至同一变量，即将x1+x2>2化归为g(x1)(或g(x2))单变量问题的解决，我们将此问题的处理方法称之为：变量归一.

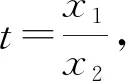
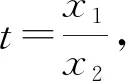
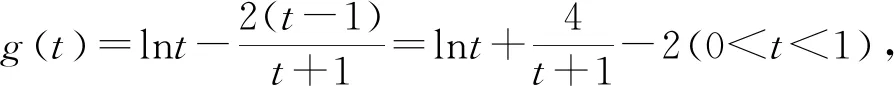
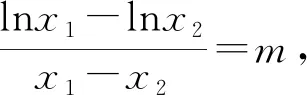
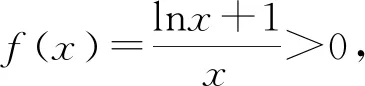
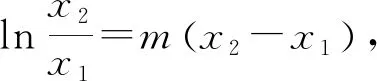
解法3，解法4以及解法5，我们可以归纳为比值(差值)变换显神通，变量归一造函数.其实，对于具体的问题，我们还会从实际问题出发，给出一些特殊的方法.比如此问题可以运用合比性质和对数平均不等式来证明，这就是笔者给出的解法6.

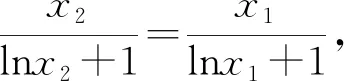
4 题目变式