合理同构，巧妙解题

甘肃省武威市凉州区职业中等专业学校 (733000) 武晓芸

在一些代数式、函数或方程、不等式、数列等问题中，同构意识是一种常见的解题意识与技巧，即通过分析其中代数式或数列通项的结构所蕴含的一些特殊的同型或共性，经过合理转化或变形，提取出其中相同或相似的结构，结合对应的数学模型加以合理构造，揭示代数式或数列通项间的内在联系，继而利用同构后的数学模型及其对应的性质来巧妙解题．

1．同构方程

涉及一些高次方程或超越方程等相关问题，经常借助原方程中相关式子的合理变形或转化，找出同型或共性，合理同构方程，利用低次方程或简单方程的应用，降维处理，巧妙转化，合理破解．

例1 (2021届江苏省镇江市高三名校10月考试数学试卷)已知实数α，β满足αeα=e3，β(lnβ-1)=e4，其中e是自然对数的底数，则αβ=________．

分析：通过对指数方程与对数方程进行两边同取对数处理，结合对数关系式的变形，寻找共性，同构方程，结合数学建模中方程的根的唯一性建立相应的关系式，通过条件的合理代换，结合关系式的变换与应用，综合代数运算加以巧妙转化与应用．

解析：由于实数α，β满足αeα=e3，β(lnβ-1)=e4，两边取自然对数可得α+lnα=3，lnβ+ln(lnβ-1)=4，即α+lnα-3=0，lnβ-1+ln(lnβ-1)-3=0，所以α和lnβ-1是方程x+lnx-3=0的根，由于方程x+lnx-3=0的根是唯一的，所以α=lnβ-1，又α+lnα-3=0，可得3-lnα=lnβ-1，整理得lnα+lnβ=4，即αβ=e4，故答案为e4．

点评：同构方程可以有效降低题目条件中方程的维度，借助同构方程进行数学建模，合理利用所构造的低次方程或简单方程的性质，变形转化，巧妙应用，很好考查数学运算、逻辑推理、数学建模等数学核心素养．

2．同构函数

涉及一些高次或超越不等式、方程等的恒成立问题，经常借助原不等式、方程中相关式子的合理变形或转化，找出同型或共性，合理同构函数，利用函数的基本性质(函数性、奇偶性、最值等)的应用，巧妙转化，得以合理确定代数式或参数的大小关系、参数的取值范围等应用问题．

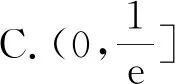
分析：通过对不等式恒成立的恒等变换，结合变形同构函数，利用所同构函数的单调性合理转化不等式恒成立问题，利用构造函数并通过求导，结合函数的单调性确定最值，进而确定参数的取值范围问题．

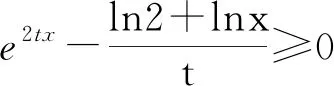
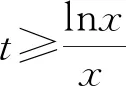
点评：同构函数可以有效破解不等式、大小比较、函数等相关问题，借助同构函数来构造相应的新函数，利用函数的基本性质(特别是单调性、奇偶性、极值、最值等)的应用，将原问题中所蕴含的内在规律外显化，揭示问题的丰富背景和相关内涵，展示同构函数的巨大魅力，很好考查数学抽象、数学建模、数学运算、逻辑推理等数学核心素养．

3．同构数列

涉及一些复杂数列通项或递推关系式等问题，经常借助数列中的关系式(通项或递推关系式)的合理变形或转化，找出同型或共性，合理同构数列，利用数列的定义、通项、求和、基本性质等的应用，巧妙转化，得以合理转化数列中的关系式(通项或递推关系式)，有效破解．

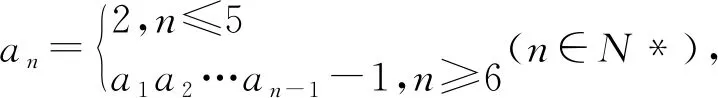
A．2019 B．2020 C．2021 D．2022

分析：根据题目条件，合理同构数列，构造新数列{bn}，通过等差数列的判断与通项公式的应用，确定新数列的通项公式，并结合递推关系式恒成立的条件建立关系式，进而得以确定参数的取值．

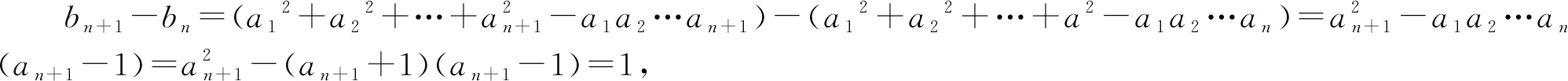
点评：同构数列可以有效破解一些比较复杂的数列问题或创新数列问题，借助同构数列来构造相应的新数列，通过递推关系式的变形与转化，利用数列的定义、通项、求和、基本性质等的应用，将原数列中所蕴含的丰富内涵加以充分展示，把复杂的数列问题简单化、熟悉化，很好考查数学抽象、数学建模、数学运算、逻辑推理等数学核心素养．

4．同构代数式

涉及一些复杂代数关系式、函数或方程等相关问题，经常借助原代数关系式中相关式子与所求代数关系式间的联系，找出同型或共性，合理同构代数式，利用相应的代数运算与转化，合理变形，巧妙转化，有效利用相关知识来合理处理与解决．

例4 若正数x、y满足xy(x-y)=4，则x+y的最小值为________．

分析：根据题目条件合理同构代数式(x-y)2与(x+y)2，通过合理变形与转化，借助平方关系的巧妙处理，合理恒等变形来转化对应的代数关系式，利用三元均值不等式来确定对应的最值问题．

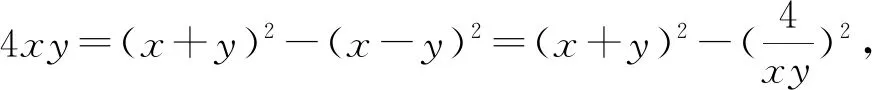
点评：同构代数式可以有效破解一些已知代数关系式求相应关系式的最值或取值范围问题、代数关系式的大小比较问题等，借助同构代数式来构造相应的新关系式，通过题目条件加以巧妙转化与变形，利用关系式的合理处理与应用，再借助相关的不等式、函数、方程等知识来分析与处理，很好考查数学建模、数学运算、逻辑推理等数学核心素养．

总之，在破解一些数学相关问题中，必须借助我们的慧眼去识别问题中的代数式或数列通项等结构的同型或共性，通过不断感知、抽象、认同、同构、建模等过程，链接熟知事物与相关知识的密切联系，合理同构，构造同型，数学建模，应用共性解题，由此增强创新意识、同构意识与创新应用，达到知识交汇，思维飞跃，形成数学能力，培养数学核心素养的目标：找同型，巧同构，证共点，用共性．