利用指对同构式巧解数学题

江苏省无锡市第一中学 (214031) 冯一成

通过“指对同构式”解决利用指数函数和对数函数构造出的超越函数问题，往往可以让原本复杂的求解过程变的简单.本文通过几个例题方法的总结和归纳，以期望呈现利用“指对同构式”解决问题的一般过程.

例1 已知对任意的x>0，不等式xex-lnx-ax≥1恒成立，则实数a的取值范围为________.

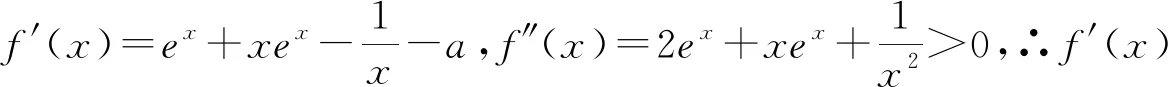
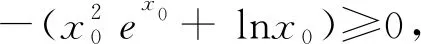
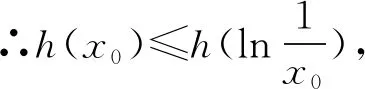
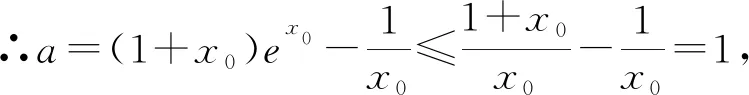
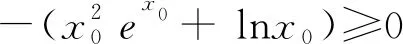
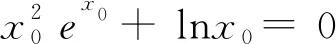
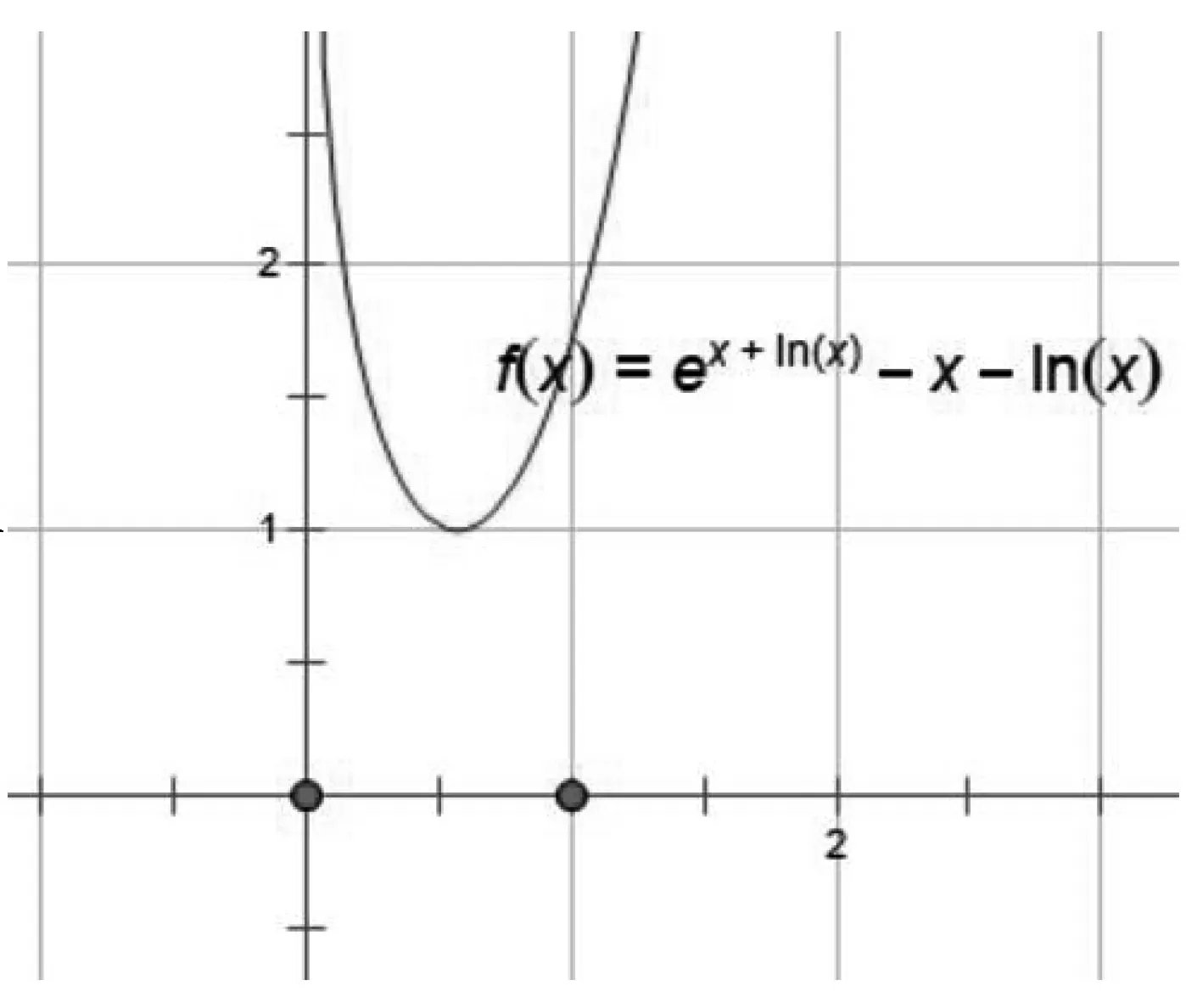
图1

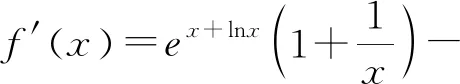
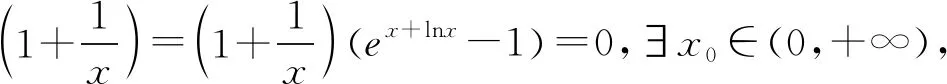
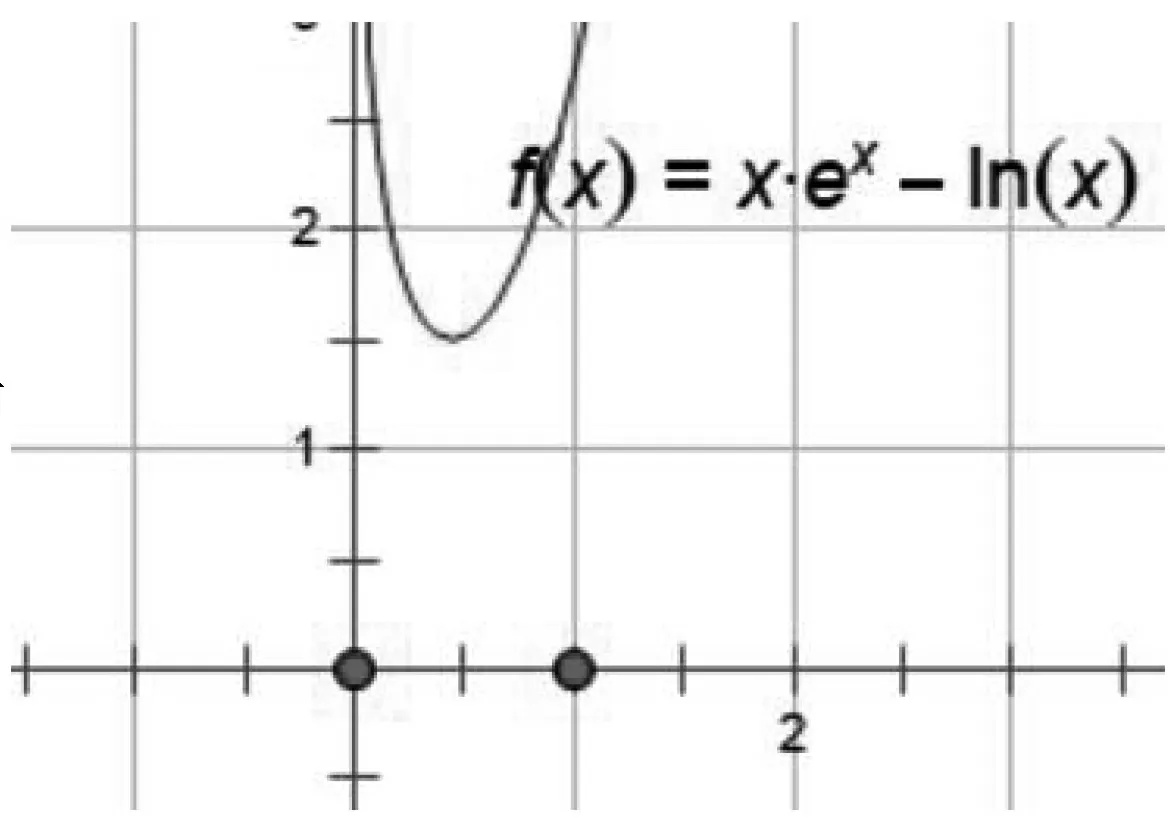
图2

点评：利用几何直观解决问题时，利用指对同构式转化原式依然是核心步骤，否则直接在不等式xex-lnx≥ax+1基础上画图，如图2则需求出过(0,1)与f(x)图像相切的直线，过程会变得非常繁琐.

方法四：(放缩法)原不等式可化为ex+lnx-lnx-x≥(a-1)x+1，此时令t=x+lnx，左式可化为et-t，利用指数不等式et≥t+1,所以et-t≥1恒成立且t=0时取等，当a≤1时，右式(a-1)x+1≤1，显然成立；当a>1时，当t=x0+lnx0=0，显然(a-1)x0+1>1不成立，故a≤1.

点评：借助指对同构式，将原不等式左侧化为ex+lnx-lnx-x为此法的核心步骤，然后借助换元法，结合常用指数不等式进行放缩，可以快速得到结果.

变式已知函数f(x)=x2e3x.当x>0时，恒有f(x)≥(k+3)x+2lnx+1，则实数k的取值范围为．

解法提示：通过“指对同构式”此题可化为e3x+lnx2-(3x+lnx2)≥kx+1.

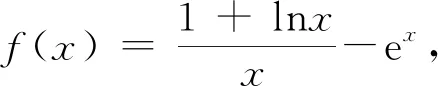
A．-1 B．-2 C．0 D．1-e