基于数学抽象的函数性质解题应用
——一次核心素养背景下的高三复习教学设计
2022-03-05福建省福清第一中学350300郭海萍福建省福清市教师进修学校350300林新建
福建省福清第一中学 (350300) 郭海萍福建省福清市教师进修学校 (350300) 林新建
函数性质是函数的重要内容,运用函数性质解决问题是高考命题的主线索,也是学习的难点.解决这类问题,必须基于函数的结构特点与模型特征,充分运用数学抽象的方法,从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,进而运用函数性质,如奇偶性、单调性、周期性、对称性等解决问题.本文以“函数性质解题应用”为例,从“感知背景、抽象特征、概括要义、辨析内涵、深化理解”五个方面入手,就数学核心素养背景下的高三复习教学设计作了一次探析,与同行分享.
1.数学情境,感知性质应用背景

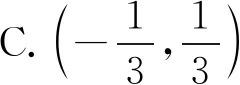
教师:你如何解这道题?直接代入解不等式吗?
学生:直接代入无法求解,太繁琐.
追问:不直接代入,我们又该如何求解呢?
设计意图:通过问题引领学生思考解决问题的方法,引起认知冲突,感知“性质应用”背景.
2.数学探究,抽象性质应用特征
问题2 你运用哪些知识来解决这个问题的?
学生:用函数的奇偶性和单调性来解决问题.
追问:你是如何想到运用这些知识来解决这个问题的?
学生:函数解析式比较复杂,直接代入求解不等式,无法完成求解,所以考虑从结构上分析函数特征,利用函数性质求解问题.
设计意图:引领学生识别函数模型,思考如何基于函数模型和性质求解问题.
问题3 (2017年福建省高三质检理15题)已知函数f(x)=x2(2x-2-x),则不等式f(2x+1)+f(1)≥0的解集是.
教师:就这个问题,你如何抽象出函数特征,并运用函数性质予以求解?
师生活动:抽象函数f(x)的模型特点,发现f(x)为奇函数,且在(-∞,+∞)上递增,从而运用奇偶性和单调性等知识解决问题.
设计意图:强化认知让学生进一步经历运用数学抽象解决问题的过程,抽象“性质应用”的特征.
3.数学体悟,概括性质应用要义
问题4你能基于上述应用,概括一下“基于数学抽象的函数性质应用”的要义吗?
师生活动:借助数学抽象的方法,抽象出函数的结构特点、模型特征、变化规律等,进而运用函数的性质,如奇偶性、单调性、对称性等分析和解决问题这个过程就是“基于数学抽象的函数性质解题应用”的过程.
问题5你能基于对“性质应用要义”的理解,概括一下常见的基本初等函数及其变换模型的结构特点、模型特征和变化规律吗?
师生活动:整理常见的基本初等函数及其结构模型如下表.
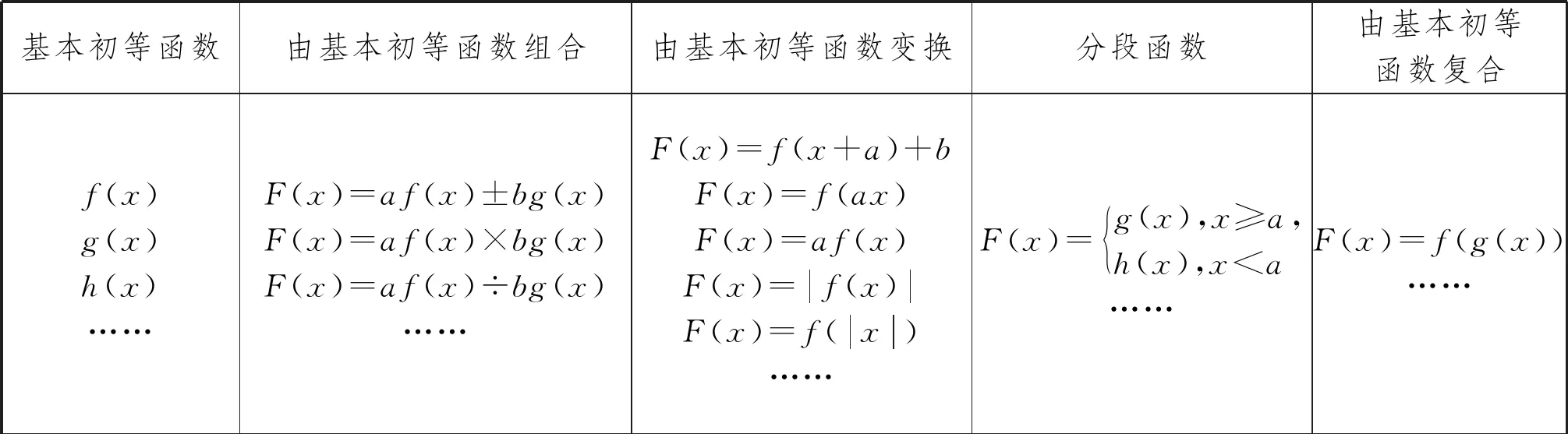
基本初等函数由基本初等函数组合由基本初等函数变换分段函数由基本初等函数复合f(x)g(x)h(x)……F(x)=af(x)±bg(x)F(x)=af(x)×bg(x)F(x)=af(x)÷bg(x)……F(x)=f(x+a)+bF(x)=f(ax)F(x)=af(x)F(x)=f(x)F(x)=f(x)……F(x)=g(x),x≥a,h(x),x 设计意图:引领学生概括“性质应用”的要义,并熟悉基本初等函数及其结构模型,为抽象函数的“结构特点、模型特征和变化规律”以解决问题做准备. 4.数学内化,辨析性质应用内涵 教师:为了更好地理解和掌握“性质应用”的内涵,我们再来思考几个问题. 评析:当函数结构较为复杂时,应等价改变其形式,向常见的基本初等函数及其变换模型靠拢,进而抽象函数模型特征,挖掘函数所具有的性质,运用性质分析和解决问题. A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞) 图1 师生活动:在本题的求解中,大多人将已知条件“函数g(x)存在2个零点”转换为“方程f(x)+x+a=0存在两个实根”,亦即“方程f(x)=-x-a存在两个实根”,所以“函数y=f(x)的图象与直线y=-x-a有两个交点”.作出函数y=f(x)与直线y=-x-a的图象(如图1),直观直线y=-x-a随变量a的变化规律,不难感知必须满足-a≤1,解得a≥-1,故正确选项为C. 评析:函数性质的应用,必须借助数学抽象的方法,抽象出函数的结构特点、模型特征和变化规律等,进而有的放矢地选择运用相关的函数性质,如单调性、奇偶性、对称性等来分析问题,则可将问题轻松予以解决. 5.数学应用,深化性质应用理解 练习(2013年高考全国卷Ⅰ理16)若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=-2对称,则f(x)=________,f(x)的最大值是________. 解析:若按常规方法求解本题,难度较大,费时费力.其实,若能抽象出函数f(x)的模型特征,则可减小运算量,最终将问题轻松予以解决.抽象函数f(x)有两个零点1,-1,而f(x)图象关于直线x=-2对称,故f(x)另有两个零点-3,-5,所以得f(x)=-(x-1)(x+1)(x+3)(x+5).再对f(x)的模型特征作抽象感知,若将f(x)的图象向右平移两个单位,则其最大值不会随之改变,因此,我们可将求f(x)的最大值转化为求函数h(x)=-(x-3)(x-1)(x+1)(x+3)的最大值.至此,直接配方即得h(x)=-(x2-5)2+16,所以f(x)的最大值为16. 评析:函数性质类问题解题的关键在于识别条件的结构特征,理解其内涵蕴意,进而确立解题方向.上述解法与命题者的参考解答相比较,另辟蹊径,独到新颖,凸显了“数学抽象”在引领特征感知、简化解题途径上的重要作用.