声发射衰减特性管道泄漏定位方法∗

张 曦 章兰珠

(华东理工大学机械与动力工程学院 上海 200237)

0 引言

管道系统在生产生活中应用广泛，对于管道系统任何潜在的或实际的结构完整性损害的检测非常重要。目前已有许多管道泄漏检测方法提出，其中声发射(Acoustic emission, AE)技术是一种被动的泄漏检测技术[1]，它对管道中的缺陷点发出的信号具有很高的灵敏度，利用声发射的长距离传播特性可有效监测管道系统[2−5]。例如，Anastasopoulos等[6]讨论了声发射产生与管道泄漏检测相关的物理问题，包括该技术的优缺点和要求，以及所需的设备。Mostafapour 等[4]建立了由泄漏引起的管道振动产生的声发射模型，并用实验进行了比较。Mao等[7]提出了一种新的声发射模型，用于现场监测桩荷载过程中地基土的性状，该模型在技术上也适用于埋地管道。

管道发生泄漏时，泄漏源连续恒定且频率成分丰富，因此记录的信号中包含多种模态的复杂混合[8]。同时，连续声发射波形缺乏可以在传感器之间识别和跟踪单个事件的时间结构，还受到散射、反射、折射和模式转换的影响，因此，使用原始声发射信号进行源定位不仅十分困难，而且通常是不准确的[9]。Shehadeh 等[10]评估了声发射连续声源在时域和频域上的畸变，认为能量衰减技术是唯一一种可用于无时间结构连续声发射源定位的方法，且可通过对特定频率成分进行滤波提高定位精度，从而为该技术所依赖的给定衰减模型提供最佳相关性。Jeong 等[11]利用声发射色散模式的小波变换来精确定位声源，并提出应在信号处理前(在动态意义上)识别声发射信号。Bianchi 等[12]提出了一种利用小波包变换提取钢轨接触疲劳试验中单个事件的方法，解决了噪声干扰声发射信号的问题。为了提高长距离管道的泄漏定位能力，Xu 等[13]提出了一种基于多级框架的泄漏定位新方法。该方法采用了区域定位和精确定位两个步骤，在精度和效率之间取得了很好的平衡。

与此同时，国内外学者们针对声波衰减特性开展了大量的工作和研究。1986年，Watanabe 等[14]提出一种检测和定位输气管道泄漏的新声学方法。当天然气管道发生泄漏时，产生声波并传播到管道的两端，过程中因为能量转化会产生衰减，然后由传感器测量以检测和定位泄漏。由于流体动力学的复杂性，声场扩散(包括速度变化和振幅衰减)难以识别，许多研究者开发了传播模型来预测声波的速度和振幅。Sun 等[15]的实验及数据分析显示1500 kHz 以下有多个频带存在不对称声传输，验证了发射频率对声波衰减的影响。Liu等[16]研究了不同截止频率下的振幅衰减系数，发现黏热效应是导致振幅衰减的主要原因。

目前利用声波的衰减特性定位泄漏已考虑了材料吸收和散射等因素，但是泄漏声发射信号频率较高且频带较宽，必须还要考虑信号频率的影响。本文首先考虑声发射波在管道中传播时受到管壁晶粒散射及热流吸收的影响，建立声发射衰减模型并实验测量不同频率成分的幅值和能量衰减系数，然后根据声发射信号时域及频域特征建立声发射源定位模型，并与传统衰减定位模型比较，验证模型的准确性。

1 声发射源定位模型的建立

1.1 声发射衰减模型的建立

1.1.1 声发射波传播原理

声发射完全具有声音的属性，它在介质中传播时，其振幅和声压会随着传播距离的增加而按照指数规律衰减，声压随传输距离衰减规律如式(1)所示：

式(1)中，P0为声源声压；P(x)为传播x距离后的声压；α为幅值衰减系数。类似的，信号的能量也有如式(2)所示的衰减规律：

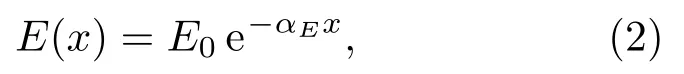
式(2)中，E0为声源能量；E(x)为传播x距离后的声发射能量；αE为能量衰减系数。声发射波在t时间内的能量为

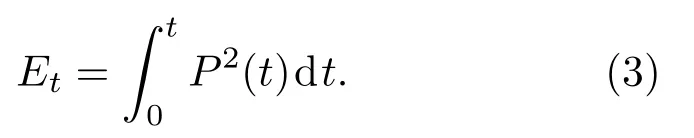
对于传感器采集的数字信号，常用式(3)计算其单位时间内声发射波能量值(即能量释放速率)：

式(4)中，fs为采样频率；s为滤波后的时域信号；s(i)为其第i个采样点的幅值；n=t/fs为采样点个数。为表述方便，后文用“能量”代替“单位时间内释放的能量”，符号用E表示。将式(1)～(3)联立可得能量衰减系数αE约为幅值衰减系数的2倍，即：

1.1.2 声发射波的衰减

引起声发射衰减的原因主要有扩散衰减、散射衰减和吸收衰减3个方面。

扩散衰减指声波向四周传播，能量也向四周扩散，随着声波传播距离的增加，单位面积的声波能量及声压降低的现象。输气管道泄漏声波在均匀管壁上传播时可看作平面波[17]，不存在扩散衰减。

散射衰减指声波在介质中传播时，因碰到各种散射体而使部分声波偏离原方向，导致原方向声波减弱的现象。散射衰减系数αS根据晶粒直径和信号波长的关系不同也有所变化[18]，声发射波长远大于无缝钢晶粒直径，可用式(6)表示：

式(6)中，Lc为平均晶粒直径；v0为纵波速；S为散射因数，是关于入射波和散射波的函数[19]。

吸收衰减：由于介质的热传导，介质的稠密和稀疏部分之间发生热交换，造成热流损失，热流衰减系数αA可用式(7)[18]表示：

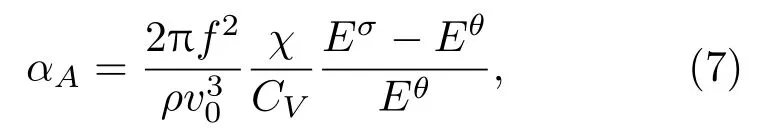
式(7)中，ρ为管道密度；χ为管道热传导系数；CV为钢管定容比热容；E为相应的弹性系数，右上角的σ、θ分别代表绝热值和恒温值。

本文将其他衰减因素如频散、相邻介质“泄漏”等先简化为α′，使声波衰减模型在工程应用上更有意义，即认为α=αS+αA+α′。实际结构中声发射衰减机制十分复杂，必须在理论分析的基础上进行实验验证。

1.2 声发射源定位模型的建立

1.2.1 泄漏检测阈值

根据声发射衰减模型，泄漏率较小或传感器距泄漏源较远时，信号中噪声能量占比突出，不仅影响定位精度，甚至几乎无法判断是否有泄漏。本文依据经验，当测得信号能量值超过无泄漏时的110%，即当测得的E(x)大于1.1Es(Es为噪声能量)时，认为泄漏产生，再进行定位。

1.2.2 传统衰减定位模型

传统的基于衰减模型定位的方法中，两个传感器放在声发射源异侧，距离分别为x1和x2，两传感器距离和L=x1+x2直接测出，距离差用式(8)计算：

于是，得到声发射源到传感器1的距离：

1.2.3 宽频带声发射源定位模型

由式(6)和式(7)可知声发射波衰减系数与信号频率的关系十分密切[15]，针对其频率较高频带较宽的特点，将传统衰减定位模型直接应用在声发射信号上会出现较大的误差。因此，本文提出宽频带声发射源定位模型，将滤波后的有效信号按照频率分解后再计算各成分对应的衰减系数，最后各成分分别定位。值得一提的是，信号在管道中持续传播可能发生频率漂移，但漂移率不超过±4%[20]，对于衰减系数的计算影响不大。

宽频带声发射源定位方法具体如下：

(1)确定小波包基函数和分解层数。

(2)根据泄漏检测阈值选择节点。

(3)计算各有效节点衰减系数，频率代入各节点中心频率。

(4)计算各有效节点能量值，利用式(9)分别定位，对各节点定位结果取均值便可得到准确的泄漏源位置信息。

1.2.4 三传感器定位模型

无论是传统的声波衰减定位模型还是本文提出的宽频带声发射源定位模型，都需要对信号进行预处理，且处理后的信号越接近真实泄漏信号，定位结果越准确。然而实际情况是无论采用何种方法组合，处理后的信号仍然含有噪声成分并且势必会丢失一部分有效信息，造成定位误差。针对信号处理带来的这些问题，本文尝试增加一个传感器，则考虑环境噪声后3个传感器能量为

式(10)中，Es1为距离声发射源x1处采集到的噪声成分的能量。各传感器处于同一环境中，假设各传感器采集到的信号中噪声能量值相等：

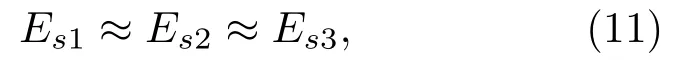
对式(10)的各传感器能量做差去除噪声干扰：

传感器之间距离L2=x1+x2、L3=x1+x3可直接测得，令式(12)比值为kE，化简后便可得定位泄漏源：

必须要注意的是，运用三传感器定位模型定位时，传感器1与传感器2、3应位于声发射源异侧。

2 声发射源定位模型的实验验证

2.1 实验平台搭建

通过观察实际输气管道系统，设计并搭建泄漏检测和定位的管道回路[21]如图1所示。实验平台由管道系统和数据采集系统两部分组成。

图1 实验管道装置结构图Fig.1 Structure diagram of experimental pipeline device

管道选用20 cm 无缝钢，由两段直管和一段弯管组成；管内气体由空压机提供，压强由减压阀控制；直管线上设有6 个直径为2 mm 的泄漏孔，泄漏状态及泄漏量通过针阀和玻璃转子流量计控制；气体中的水滴和油滴在通过油水分离器时被清除。

数据采集系统主要包括声发射传感器、信号放大器和声发射采集仪三块。传感器选择RS-2A型传感器，频率范围0～400 kHz，中心频率150 kHz，对0～230 kHz的信号检测灵敏度达60 dB以上，可在−20°C～130°C下正常工作；前置放大器选择固定增益型，放大倍数40 dB；采集仪选用北京软岛公司DS5-8A 型全信息声发射信号分析仪，最多可支持8个信号通道同时进行工作。

2.2 声发射衰减系数测量

2.2.1 泄漏声发射信号频率范围

将传感器安装在距离泄漏源0.5 m 处采集管道泄漏信号，采样频率fs= 2.5 MHz，管道内气压0.3 MPa。调节针阀设置不同泄漏率，检测得到信号时域图2所示，可以看出，有泄漏时信号的幅值比无泄漏时有所增加，且随着泄漏率的增大，幅值也相应增大。对泄漏信号做快速傅里叶变换后的频域图如图3所示，从图像上可以直观地看出，当泄漏率增大时，0～200 kHz 频率的信号幅值也增大，尤其在8～80 kHz频率范围，幅值增加非常明显；而频率高于200 kHz的信号的幅值并无明显变化。

图2 管道泄漏信号时域曲线Fig.2 Time domain curve of pipeline leakage signal

图3 各泄漏率下泄漏声发射信号频谱图Fig.3 Spectrum diagram of acoustic emission signal under different leakage rates

为验证泄漏信号的频率范围，将信号利用小波包函数进行细致地划分，观察各小波子带能量变化。小波基选择‘coif5’，分解层数5 层，各节点能量分布如表1所示，表中能量变化率为2 L/min 泄漏率工况与无泄漏工况做比较。由表1可清楚地看出，产生泄漏后，[5,0]、[5,1] 和[5,3]这3个节点能量变化在250%以上，[5,2]和[5,6]两节点的能量变化在50%以上，其余节点能量变化都不超过10%。根据泄漏阈值，认为泄漏信号能量主要集中在这5 个节点，即频率在196 kHz以内。

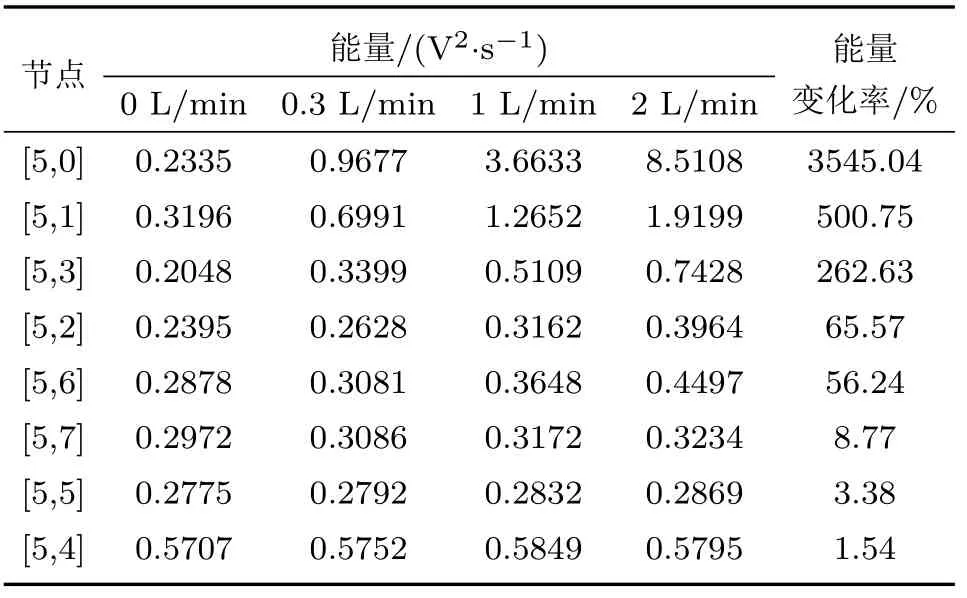
表1 泄漏信号5 层小波包分解分量能量Table 1 5-layer wavelet packet decomposition component energy of leakage signal

2.2.2 泄漏信号衰减系数

图4为声发射衰减系数测量实验框图。实验时，由Tektronix AFG3021C 任意波形发生器在管道的一端发射固定频率的突发信号，两传感器在管道另一端接收，相距Δx。MATLAB 提取信号的幅值和能量值后，通过式(5)可计算实际声发射衰减系数。

图4 声发射衰减系数测量实验框图Fig.4 Experimental block diagram of acoustic emission attenuation coefficient measurement

图5为当发射频率为120 kHz、幅值为10 V 的信号时，两传感器接收信号的时域图，可以看出，距离信号源较远的传感器2 接收到的幅值和能量较低。分别计算不同频率声发射信号的幅值和能量衰减系数，如图6所示。实验结果表明，衰减系数与f4和f2有关，且能量衰减系数约为幅值的2 倍，也就是说，能量对声发射信号的衰减比幅值更敏感，所以在利用衰减系数进行泄漏源定位时，通常选用能量参数。

图5 不同距离接收到的信号Fig.5 Signals received at different distances

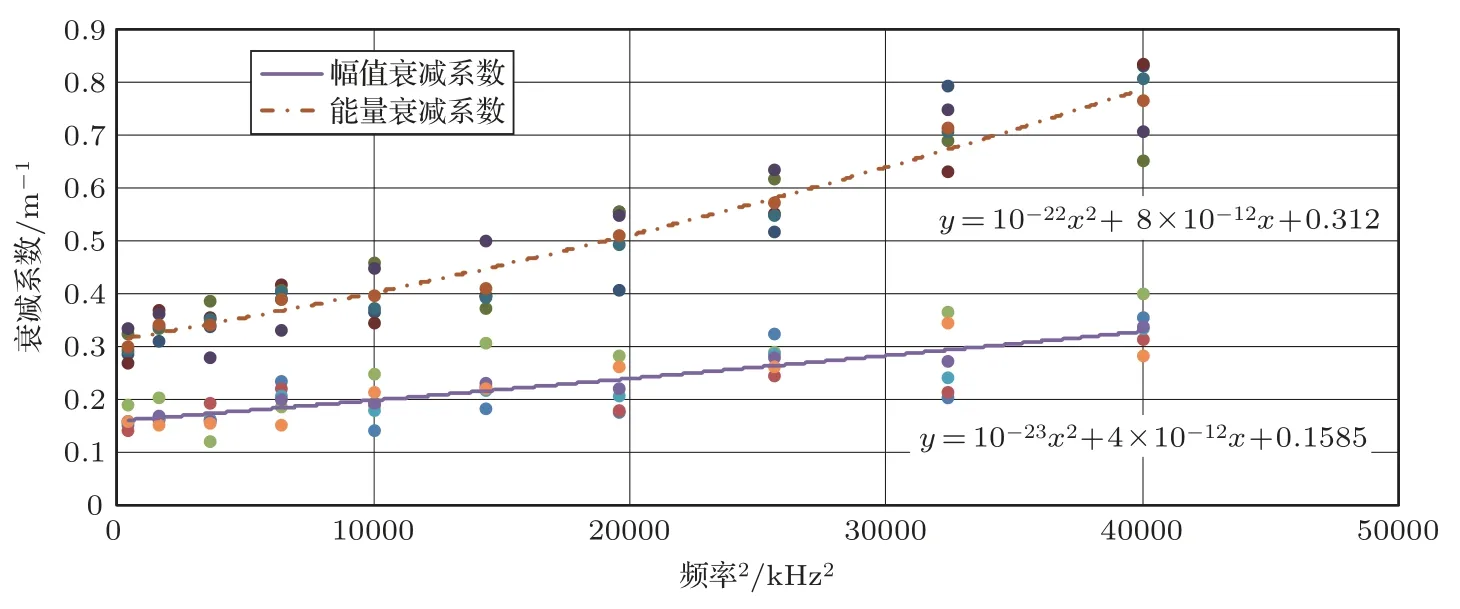
图6 信号衰减系数与频率的关系Fig.6 Relationship between signal attenuation coefficient and frequency

2.3 声发射源定位模型实验验证

2.3.1 声发射源定位实验

定位实验传感器布置如图7所示，传感器与泄漏源距离如表2所示。实验分为两部分：第一部分研究宽频带定位模型的定位精度，使用两个传感器，实验结果如表3所示，其中误差为预测泄漏位置与实际泄漏位置之差除以两传感器之间距离的一半；第二部分研究增加一个传感器后对定位精度的影响，实验结果如表4所示。

表2 传感器布置Table 2 Sensor arrangement

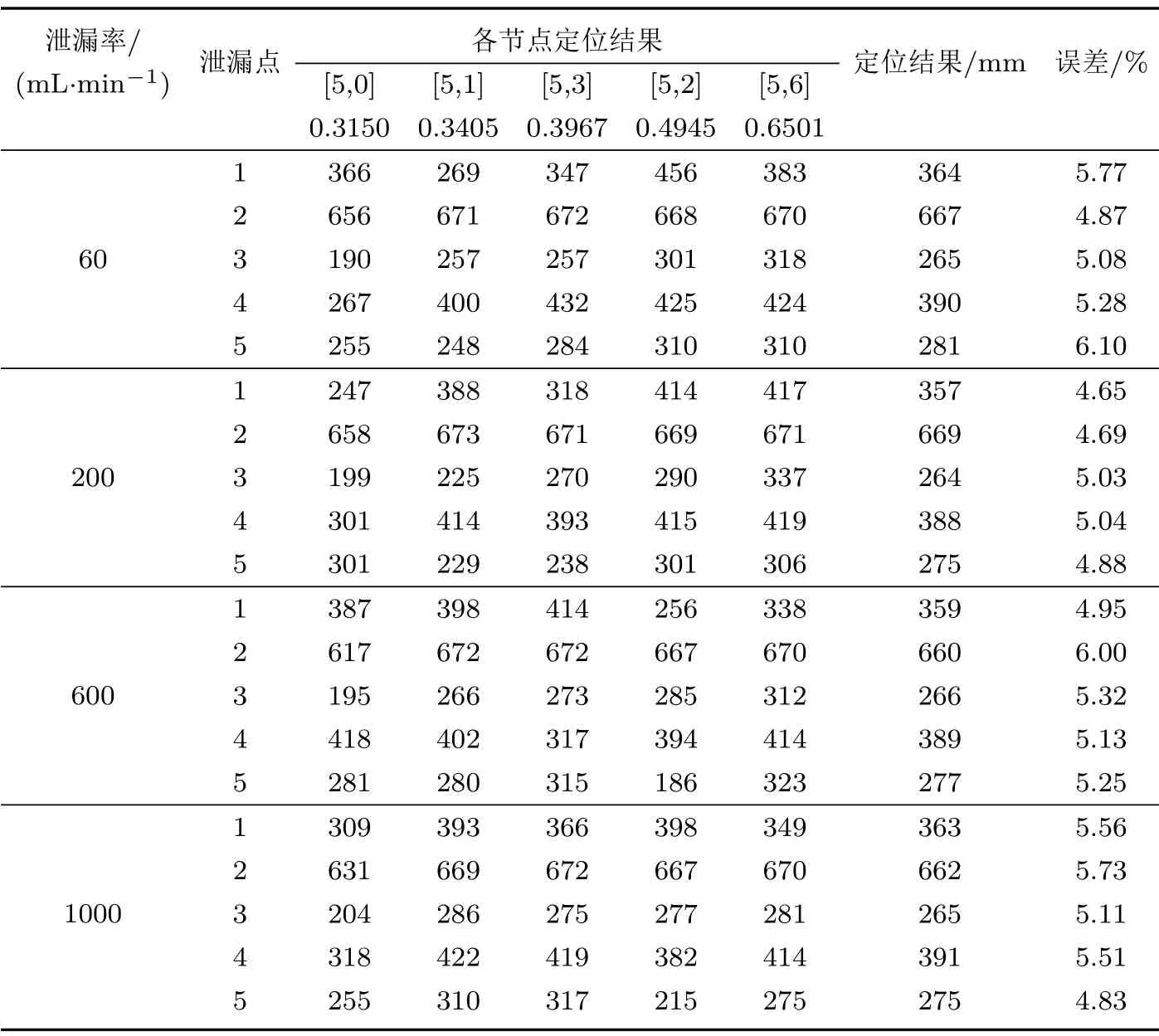
表4 三传感器定位模型后定位结果Table 4 Location results of three-sensor positioning model

图7 声发射源定位示意图Fig.7 Schematic diagram of acoustic emission source location

在传统衰减定位方法中，一般只保留信号中能量占比最大的成分来计算衰减系数并进行定位，其他成分直接滤除。根据图3，泄漏声发射信号中8～30 kHz 的信号变化最明显，将这部分信号成分提取出来，衰减系数αE=0.3150 m−1，代入实验一的信号得到结果如表5所示。

表5 传统衰减定位模型定位结果Table 5 Localization results of traditional localization model

2.3.2 声发射源定位模型检测范围

以泄漏阈值作为检测泄漏的标准，结合实验验证的衰减模型，得到声发射源定位模型各泄漏率下的适用范围如图8所示。

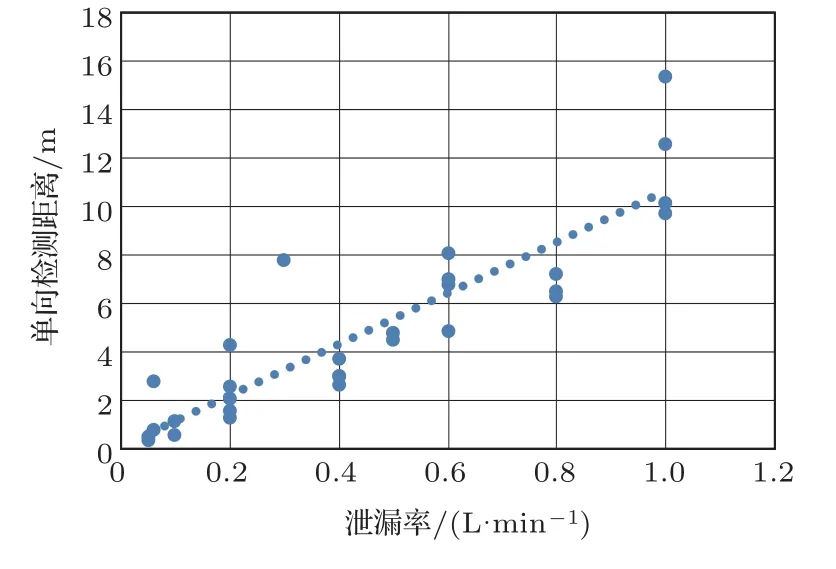
图8 声发射源定位模型适用范围(单侧)Fig.8 Applicable range of acoustic emission source location model(unidirectional)

3 讨论

由表3～5可知：

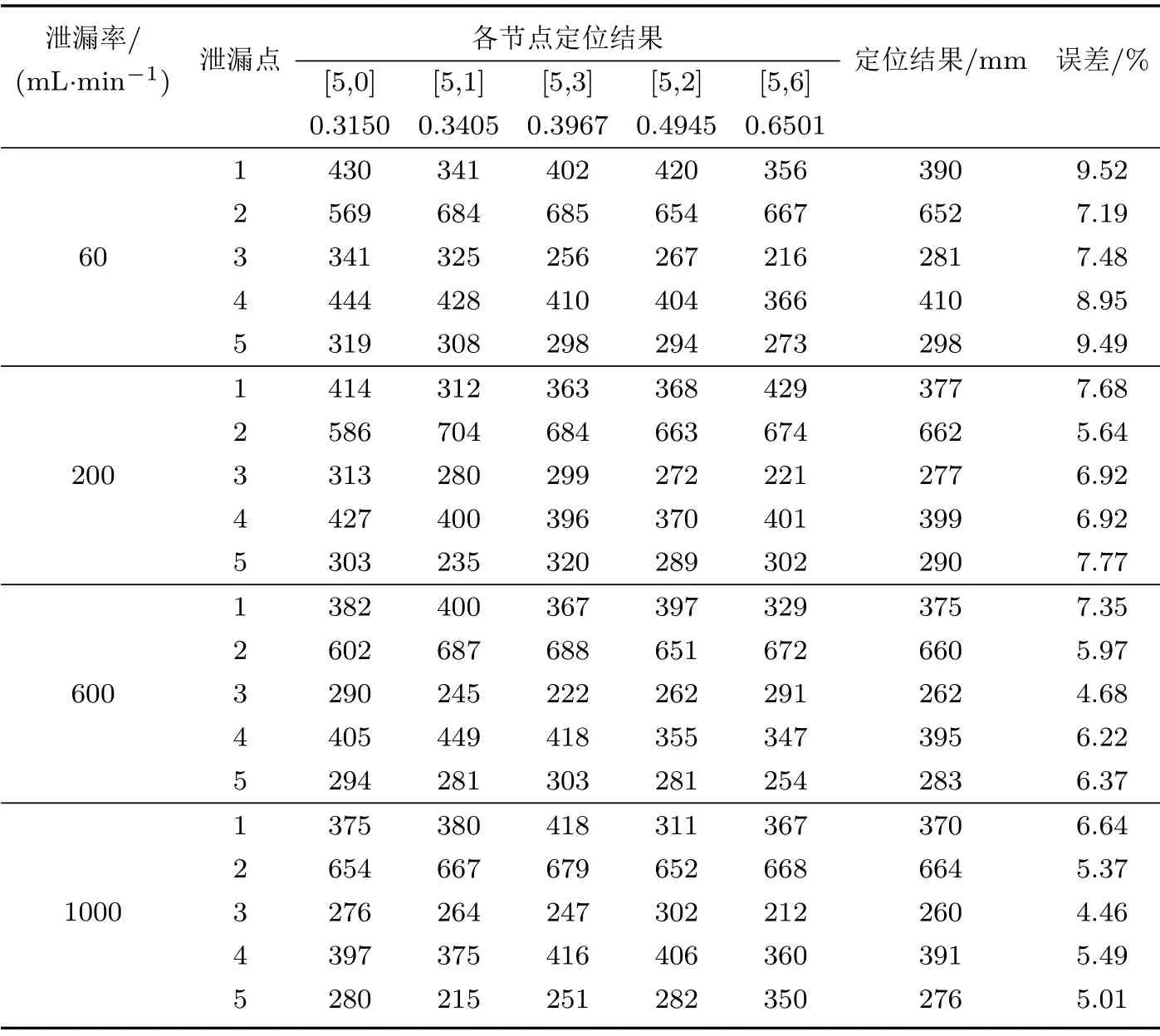
表3 宽频带声发射源定位模型定位结果Table 3 Location results of wide-band acoustic emission model

(1)传统衰减定位模型的定位误差在20%以内，且随着泄漏率增大，定位精度显著提高，当泄漏率高于600 mL/min时，定位误差低于9%；

(2)宽频带定位模型的定位误差在10%以内，随着泄漏率增大，定位精度也有所提高。该模型平均误差比传统定位模型减小5 个百分点，尤其在泄漏率为60 mL/min时减小了8个百分点；

(3)三传感器定位模型定位误差在5%左右，几乎不受泄漏大小的影响，说明通过作差法能够有效降低噪声成分的干扰。

误差来源：(1)管道结构：支管、焊缝等结构对声波的吸收和散射未考虑，使得声波衰减规律并不完全服从指数规律。(2)信号采集不准确：来源于采样频率的限制和不同传感器之间的误差。声发射仪的最低采样频率为2.5 MHz，远超泄漏信号有效频率(200 kHz)的两倍，过高的采样频率使采集到的数据量过大，包括许多不必要的环境信息；若要减少计算量及节省存储空间势必使得采样时间过短，导致许多有效信息被排除在外。同一工况同一采样位置，不同的传感器采集的信号幅值不相同。(3)信号处理的误差：小波包分解信号的过程并不严格，各节点之间的频率会有混叠，需对信号处理方法进一步改进。(4)实验误差：泄漏通过阀门开启实现，泄漏量通过流量计确定。虽然操作过程中已尽量模拟实际中的工况，但误差难免存在，造成信号数据的浮动。

4 结论

(1)泄漏声发射波在管道上传播的模式为一维平面波形式，其传播过程受到金属晶粒散射作用和热流效应的影响。考虑以上因素本文从理论上建立了声波幅值和能量的衰减模型，并利用实验得到了准确的衰减系数。

(2)泄漏声发射频率集中在8～197 kHz，频带较宽。本文对传统衰减定位模型进行优化，提出了宽频带声发射源定位模型，将声发射信号利用小波包进行分解，根据各节点中心频率计算衰减系数，从而提高定位精度。实验证明使用宽频带定位模型时，定位误差平均减小5 个百分点，在泄漏率为60 mL/min时可减小8个百分点。

(3)针对处理后的信号中仍存在的噪声分量，本文提出通过增加一个传感器，利用3 组信号互相做差的算法提高定位精度。实验证明，增加一个传感器可有效减小噪声的影响，定位误差约为5%。相比于传统模型和宽频带模型，该方法操作和计算均复杂一些，更适用于低泄漏率、高定位精度的情况。

(4)本文提出的宽频带定位模型在计算声波衰减系数时，简单地使用各小波包节点的中心频率，未考虑各节点内部各频率成分能量的分布，这可作为进一步研究方向。