非线性兰姆波在阶梯板中传播的有限元仿真∗

孔媛媛 安志武

(1 中国科学院大学 北京 100049)

(2 中国科学院声学研究所 声场声信息重点实验室 北京 100190)

0 引言

超声导波在无损检测领域有广泛的应用。非线性导波检测则利用了导波信号对亚波长缺陷的非线性响应，如高次谐波、次谐波、和频、差频波等信号，实现对微结构的无损检测。理论上对导波的波形进行信号分析，即可以对缺陷进行有效的检测和表征，然而影响导波波形的因素有很多种，如导波波形会受到被测结构的几何形状的影响，在波导的几何形状不连续的地方会发生散射。研究波导结构的几何形状对导波波形的定性和定量影响，对导波无损检测的实际应用具有重要指导意义。

通过数值模拟、实验观测和理论推导等方法，线性兰姆波在变厚度板中的传播性质已经得到了充分的研究。数值仿真方面，Cho[1]用有限元方法研究了变厚度板中兰姆波的模式转换特征；沈意平等[2]用有限元仿真了线性兰姆波在变厚度板中的模态转换特性。实验观测方面，张旭等[3]运用动态光弹法研究了A0 模式的兰姆波在台阶板中的传播特性。Marical 等[4]利用数值仿真和实验观测了兰姆波在板厚高斯函数缓变的薄板中的传播规律，文章观测到了兰姆波在厚度缓变处满足绝热模态的传播条件，且在厚度变化为高斯函数的区域观测到了束缚模态(trapped mode)，并定量研究了兰姆波的反射和透射系数。理论计算方面，Schaal等[5]用最小二乘法推导了兰姆波在台阶板中的传播过程，给出了兰姆波在台阶板中传播的解析解。Pagneux 等[6]利用兰姆波的正交性质，用模式展开法给出了兰姆波在厚度连续变化板中的解析解。Feng等[7]利用模式展开法，对任意几何截面的板状波导进行阶梯状的离散，并给出了散射矩阵的具体表达式。

二次本构关系下滋生的非线性兰姆波在均匀板中的传播，也已得到了较为完备的研究。Deng[8]、Lima 等[9]先后采用了部分波法和模式展开法研究了非线性兰姆波二次谐波在固体板中的传播，得到了兰姆波二次谐波声场的解析解。结果表明，伴随基频兰姆波传播产生的二次谐波需要满足一定的共振条件才会表现出振幅随传播距离累积增长的性质，这样的共振条件是：二倍频兰姆波模式与基频兰姆波相速度相等，且基频兰姆波有非零能流馈入二次谐波。其他与基频兰姆波相速度不等的二倍频兰姆波模式，其振幅随距离传播出现拍效应。基于这些研究结果，发展出了非线性混频检测方法，该方法既利用了非线性效应对微损伤的灵敏度，也在克服了非线性现象无法精准定位损伤位置的缺点。非线性兰姆波在厚度非均匀板中的研究还比较欠缺，Hu 等[10]通过理论计算和有限元仿真研究了厚度缓变板中S0 模式的非线性兰姆波的传播特征，得到了兰姆波在厚度缓变板中的传播规律，文章发现，满足绝热条件的兰姆波模式在厚度缓变板中依然存在与匀厚板中类似的累积效应和拍效应。综上所述，针对二次谐波在均匀导波中的传播规律，已有较为完整的研究，得到了二次谐波幅值的增长规律；而针对非均匀板中的传播规律，相关的研究还较为缺乏，只研究了厚度近似均匀、厚度缓变的情况。

本文通过有限元仿真模拟了非线性兰姆波的S0 模式在台阶板中的传播特征，并选择S0-S0 兰姆波模式对。仿真中只考虑几何非线性和本构关系非线性，本构非线性采用Murnaghan 模型[11]。本文主要由4 部分组成，第一部分介绍了有限元仿真过程，包括几何模型建立、本构模型建立以及反射波的抑制；第二部分介绍了仿真信号的后处理方法，给出了二维离散傅里叶变换结果和兰姆波模态幅值的对应关系，以及兰姆波模态能流的计算方法；第三部分介绍了匀厚度板中非线性兰姆波传播的仿真结果，通过验证谐波模态和累积二次谐波的增长周期证明了仿真程序的可靠性；第四部分给出了阶梯板中非线性兰姆波的仿真结果，通过二维离散傅里叶变换验证了传播模态和二次谐波滋生的过程，并给出了不同厚度阶梯板结构中非线性兰姆波的基波和二次谐波的透射、反射系数。

1 阶梯板的有限元建模

1.1 阶梯板几何模型建立

阶梯板的模型如图1所示，进行二维平面应变仿真，主要参数为厚度差height_dif。分析区域总长为1000 mm，在A、B两点处施加激发信号，即为信号传播的起始点，激发出兰姆波后沿x正方向传播1000 mm 后被吸收，吸收层的总厚度为100 mm，信号向左传播100 mm 后也进入一个100 mm 的阻尼吸收层。

图1 有限元仿真几何模型Fig.1 Geometry of finite element simulation

1.2 阻尼吸收层的设置

通过修改吸收层材料的瑞利阻尼来吸收传入的兰姆波，以减小反射回波。将100 mm长的吸收层平均分成40个子层，每段子层长2.5 mm，材料设置为线弹性材料，吸收层材料的拉梅系数与传播区域的材料拉梅系数相同，每一子层的瑞利阻尼不同，设第i层的瑞利阻尼为αi。序号按照兰姆波的传播方向依次编号，即入射波依次入射第1 层、第2 层···以此类推。瑞利阻尼设为[12]

其中，αmax=1.5×106。两侧吸收层都按照这样的规律进行设置。

1.3 材料本构模型参数设置

分析区域的材料定义使用Murnaghan 模型，分析区域的材料参数设置如表1所示。

表1 材料参数Table 1 Material parameters

图1中标记的分析区域以及分析区域左侧100 mm 长的区域与分析区域均使用表1中的材料定义；其他区域的材料使用线弹性本构关系，杨氏模量和泊松比的取值采用表1，吸收层参考第1.2 节额外定义瑞利阻尼系数。

2 信号后处理方法

2.1 离散二维傅里叶变换与频率波数域的转换关系

仿真过程中所得的位移信号可以看作关于位置和传播时间的二维离散信号，对信号进行二维傅里叶变换可以得到信号在波数-频率空间的分布规律，从而得到关于各个传播模态的有用信息。二维傅里叶变换将位移值分解成不同波数、频率沿x方向传播的行波之和[13−14]，离散二维傅里叶变换将时间空间域的二维矩阵u变换成相空间的矩阵：

其中，方括号中的两个参数分别为矩阵的行列编号，M为空间采样点数量，N为时域采样点数量。记时域采样频率为fs，空间采样频率为f′s，时域采样间隔为Δt，空间采样间隔为Δx。有限元仿真所得数据是对板表面的面内位移或离面位移在时间、空间上均匀采样得到的M行N列的矩阵：

本文采用的时间、空间采样点数、采样率和采样间隔如表2所示。

表2 采样信息Table 2 Sampling parameters

当M或N为奇数时，将M/2、N/2 分别替换成(M+1)/2、(N+1)/2 即可，由二维傅里叶变换的对称性，频率轴只有一半的有效值，只取频率轴的前半部分。频率波数域的转换关系对应图2(a)和图2(c)，相空间的上半部分的波数为正值，下半部分的波数为负值，图2(a)中M和N均为偶数，图2(c)中M和N均为奇数。为了和频散曲线相对照，需要整体交换上下平面的顺序，使波数的零点位于波数轴的中间，交换后的结果如图2(b)和图2(d)所示。此时第(p+1)行元素对应的波数为

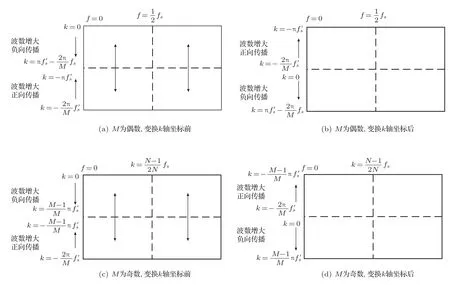
图2 二维离散傅里叶变换矩阵与频率波数的对应关系Fig.2 Matrix obtained by discrete 2D Fourier transform and its relationship between wave number and frequency

频率为f的正向传播的模态n兰姆波在均匀板中的位移场为

表达式为复数形式，取表达式的实部表示实际位移值。下标为模态编号，上标表示频率，模态n的波数由频散关系确定，令kfn >0。模态n在薄板上表面的离面位移可以写成行波的形式：

比较式(3)和式(10)，可知二维傅里叶变换结果和兰姆波模态振幅有如下对应关系：

图2(a)中，上半部分的波数为正，代表负向传播的兰姆波模态，下半部分的波数为负，代表正向传播的兰姆波模态，经过二维离散傅里叶变换后的二维矩阵与对应波数和频率的兰姆波模态一一对应的关系，波数对应关系为式(8)，频率对应关系为式(7)。

2.2 透射系数和反射系数的定义

参考Morvan等[15]的定义方式，定义系数：

该系数将理论的表面振幅U(h)与通过横截面的能流φ联系起来，S0 模态ξ的理论值与频厚积的关系如图3所示，其中材料参数的定义参考表1，每条线都表示不同的厚度板的计算结果，从远离原点到靠近原点的方向，依次表示厚度为4000 µm、3400 µm、2800 µm、2200 µm、1600 µm、1000 µm、400 µm 的薄板中的计算结果。其中空心圆对应150 kHz，星标对应300 kHz，分别对应有限元仿真中的基波和二次谐波的频率。

图3 不同厚度板中的兰姆波ξ 值Fig.3 The value of ξ in plate with different thickness

经过二维傅里叶变换，可以求得信号在相空间(k,f)的分布，即第n阶兰姆波在给定频率f下的位移幅值，根据式(11)和式(12)，可以求出第n阶兰姆波模态的能流：

图4列出了阶梯板中各个模态的能流分布情况，φinnc(f)表示频率为f的入射模态n，下标为模态编号，上标inc 表示入射波，若上标为r表示反射波，t表示透射波。基频、二次谐频S0 模态的透射、反射系数的定义为

图4 各阶模态兰姆波能流Fig.4 Power flux of each Lamb mode

这里的反射与透射系数的定义与界面反射投射系数的定义类似，表示了特定频率透射和反射波能量占入射波能量的比值。若只考虑入射和反射，反射、透射系数一般都小于1。

3 均匀厚度板有限元仿真结果与理论验证

3.1 激发条件

首先针对厚度差height_dif为零的情况进行仿真，即板厚均匀的情况，板厚设置为4 mm。按照理论预测，满足共振条件的S0 模式兰姆波会产生出S0 模式的二次谐波。改变激发信号的中心频率f0，分别设为150 kHz、170 kHz、190 kHz、210 kHz，在A、B两点上下对称地施加传播方向的位移约束u(t)。图5为S0模式兰姆波的波结构图，位移值均已用二范数进行归一。实线表示面内位移，即x方向位移，虚线表示离面位移，即y方向位移。图5(a)～图5(d)分别表示频率为150 Hz、170 kHz、190 kHz、210 kHz 的S0 模式兰姆波波结构。振动模式包含x方向和y方向的位移，在150～210 kHz 频段，面内位移振幅大于离面位移振幅，振动模式以面内位移为主。仿真过程中，统一在A、B两点施加相同的面内位移约束u(t)，以激发出想要的S0 模态，振幅大小为5 µm，u(t)为经过汉宁窗调制的18 周期正弦波，中心频率分别为150 kHz、170 kHz、190 kHz、210 kHz。中心频率为150 kHz 的激发信号的时域和频域曲线如图6所示。

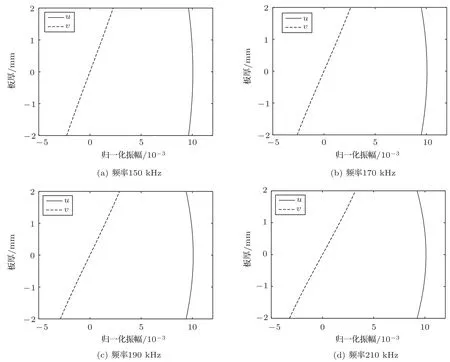
图5 S0 模式兰姆波波结构图Fig.5 Wave structure of S0 mode Lamb wave

每隔1 mm 接收一次板表面(y=h)处的位移信号，共得到1000 组不同传播距离的位移信号。图6(c)和图6(d)分别为中心频率为150 kHz 时，传播距离为500 mm 处，x方向的时域位移信号u(t)和经过傅里叶变换的频域信号˜u(f)，从频谱反映出位移信号包含基频(150 kHz)和二倍频(300 kHz)成分，和激发信号相比滋生出了二次谐波信号。

图6 激发和接收信号Fig.6 Excitation and receiving signals

3.2 累积二次谐波增长规律验证

对1000 个接收点接收到的时域信号依次做傅里叶变换，提取二倍频处的幅值，不同激发频率下二次谐波幅值随着传播距离的变化如图7所示。由于吸收层无法将兰姆波完全吸收，仍然存在微弱的反射波，故经过傅里叶变换的二次谐波幅值受到了反射波波包中二次谐波成分的影响，存在一定的抖动，但基本上可以反映兰姆波二次谐波随距离的传播规律，类似的两个波包存在时进行傅里叶变换所导致的抖动在阶梯板中有更明显的体现。为了避免这样的影响，对时间信号统一做截断，可以发现，在0～400 mm 处的二次振幅演化曲线的抖动明显减轻，这是因为在这段传播距离内没有截取到反射波包，传播到此处的时域信号仅包含一个波包。

图7 二次谐波振幅随着传播距离的变化Fig.7 The relationship between the amplitude of second harmonics and propagation distance

当相速度匹配条件近似满足时，二次谐波的幅值呈现周期震荡，理论震荡周期为[7]

其中，kω0和k2ω0的下标表示S0 模态，上标表示该波数所对应的频率。产生累积二次谐波的条件为，对于传播模态，即为k2ω0=2kω0，满足匹配条件时，理论震荡周期趋向无穷大，当这个条件近似成立时，相速度越匹配，震荡周期越大，累积增长的距离越长。利用理论公式和有限元仿真分别求得的二次谐波震荡周期如表3所示。

表3 二次谐波振幅增长周期的理论解和仿真结果Table 3 Theoretical and simulated solutions of the period of accumulation

3.3 激发模态验证

下面只考察信号中心频率为150 kHz 时得到的位移信号，每隔1 mm接收一次上表面(y=h)处的x方向位移信号，将这1000 组信号组合成一个位移矩阵。如图8所示，位移矩阵的灰度图如图8(a)所示。灰度图的横轴表示接收点的位置，对应的纵轴为时间轴，灰度表示振幅的大小，图8(b)为距离接收点500 mm 处所接收到的时域波形，将其振幅转换成灰度图表示，如图8(c)所示，即为图8(a)灰度图的第500列。

与图6(c)类似，图8(b)有轻微抖动，主要原因是兰姆波在边界处的反射。本文通过增大仿真边界处材料的瑞利阻尼减少兰姆波的反射，只能减少反射波的产生，无法消除所有反射波。在3.2节已有阐述，此次不再赘述。

图8 各点接收到的位移信号组成的二维矩阵Fig.8 The matrix representing displacement signals received at different positions

对位移矩阵进行二维傅里叶变换，可以得到信号在波数-频率域的分布情况，如图9所示，同样也用灰度图表示，横轴表示频率，纵轴表示波数。图中的白色虚线为对称模式的频散曲线，白色实线表示反对称模态的理论频散曲线。可以发现，在基频和二次谐频处均激发出了向x轴正向传播的S0 模式的兰姆波模态。

图9 二维离散傅里叶变换结果Fig.9 The result of 2D discrete Fourier transform

综上所述，仿真得到的二维傅里叶变换结果与理论频散曲线相吻合，S0 模式的基频兰姆波激发出了S0 模式的二次谐波。同时仿真所得的二次谐波的增长周期也与理论预测基本吻合，误差在5%以下，验证了仿真程序的正确性。

4 S0模式非线性兰姆波在阶梯板中传播的有限元仿真结果

4.1 基本传播规律

材料参数不变， 固定激发信号的中心频率为150 kHz，只改变两个阶梯板之间的厚度差height_dif， 分别将厚度差设置为3600 µm、2400 µm、1800 µm、1200 µm、600 µm、0 进行仿真，各个传播距离接收到的时域波形图如图10 所示。可以观察到，在厚度突变处，部分兰姆波发生反射，且反射波的振幅随着厚度差的增大而增大，入射波和透射波的相速度和群速度保持不变。其中入射波和透射波的群速度约为5230.4 m/s，反射波的群速度约为−5437.0 m/s。对每个接收点处的时域信号进行傅里叶变换，取二次谐波信号，可以得到兰姆波的二次谐波随传播距离的变化规律，如图11所示，可以看到，传播距离为0～500 mm 时，二次谐波的振幅剧烈的抖动，表示不同接收点处入射和反射波包的傅里叶变换结果。传播距离大于500 mm时，兰姆波的累积效应随着厚度差的增大而增大，此处S0 模式的基波和二次谐波的相速度匹配程度随着频厚积的减小而增大，累积效应增大。

图10 不同阶梯高度下的位移时域仿真结果Fig.10 Simulated time-domain displacement signal with different step heights

图11 二次谐波幅值随着传播距离的变化Fig.11 Variation of the amplitude of the second harmonic wave with respect to propagation distance

4.2 模态分析

由于兰姆波在不同厚度的板中的频散关系不同，需要对传播距离小于500 mm 以及大于500 mm 的时域位移信号分别进行二维傅里叶变换。设仿真所得的所有信号为u(xi,tj)，其中0 ≤xi≤1000 mm，0 ≤tj≤6×10−4s，空间采样率为1 mm，仿真结果可以组成一个1000 行的矩阵，对这个矩阵进行分块，分成前500 行和后500行，分别进行二维傅里叶变换。图12 是入射和反射波的波数-频率域分布情况，即对前500 行位移信号的傅里叶变换结果；图13 是透射波的波数-频率域分布情况，即对后500 行位移信号的傅里叶变换结果。图12 和图13 上均叠加了理论频散曲线，可以看到，图13 叠加了厚度为4 mm 时的频散曲线，图12上叠加的频散曲线各不相同，其对应的厚度为(4 mm-height_dif)，即薄端的频散关系。

图12中可以观察到两个方向的传播模态，既有波数为正的模态也有波数为负的模态，说明在厚端出现了两个方向传播的兰姆波，即入射波和反射波。每个传播方向又可以观察到基频波和二次谐波成分，分别对应150 kHz 和300 kHz，所有模态都与S0模态的频散曲线重合，说明两个方向传播的基波和二次谐波均为S0模式。色阶图也分别反映出了这4个模态的能量大小，反射波的二次谐波能量随着阶梯板的厚度差不断增大。图13 中只能观察到一个方向的传播模态，只有入射波，随着厚度差的增大，S0 模式的频散曲线在低频处越趋向于一条直线，透射波二次谐波的幅度不断增大，而且也更容易滋生S0 模式的高次谐波，因为此时各个高阶模态的相速度几乎相同，满足相速度匹配的条件。

图12 入射和反射波二维离散傅里叶变换结果Fig.12 2D discrete Fourier transform of incident and reflected waves

4.3 透射和反射系数的计算和分析

基于图12 和图13 所示的二维离散傅里叶变换结果，可以分别提取出入射、反射和透射的基波和二次谐波振幅。利用公式(15)可以计算出不同频率、不同传播方向模式兰姆波通过横截面的能流大小，相应的透射和反射系数与能量转换关系，入射和反射系数的定义见公式(16)。图14 分别为基波、二次谐波的透射和反射系数，实线为基波、虚线为二次谐波。阶梯板厚度差增大，向薄端入射的基波幅值整体呈下降趋势，反射系数单调增加。随着阶梯板厚度差增大，二次谐波的透射系数先增大后减小，且出现了透射、反射系数大于1 的情况，这与能量守恒关系并不矛盾，根据公式(16)的定义，透射和反射系数中的分母均为入射二次谐波的能流大小，透射和反射的高次谐波的能量大于入射二次谐波的能量，是传播过程中基波能量向高次谐波馈入的结果。图15 为入射、反射和透射波中二次谐波和基波的能流之比。对于入射波，波导厚度相同、传播距离相同的情况下，二次谐波的能流与基波的能流之比不随阶梯板厚度的增大而改变。对于反射波，累积二次谐波的幅值也与波导厚度、传播距离相关，二次谐波能量与基波能量之比应该保持不变，但是在非线性谐波散射问题中，二次谐波的来源有两种，反射基波的谐波滋生、入射二次谐波的反射。由于反射二次谐波的能量随着阶梯板厚度的增加而增加，反射波的二次谐波能量与反射基波的能量之比也随着阶梯板厚度差的增大而逐渐增大。可以看到，在阶梯板中，由于散射的存在，反射二次谐波的幅值不仅与传播距离相关，而且会随着反射的增强而增大。

图13 透射波二维离散傅里叶变换的结果Fig.13 2D discrete Fourier transform of transmitted waves

图14 基波和二次谐波的透射和反射系数Fig.14 Transmission and reflection coefficient of fundamental and second harmonic waves

图15 入射、反射、透射波中二次谐波与基波能量之比Fig.15 The power flux ratio of second harmonics to fundamental waves of incident, reflected and transmitted waves

5 结论

本文利用有限元研究了非线性兰姆波在本构非线性阶梯板中的产生、传播和散射现象，并分析了相关传播规律。基于均匀板中累积二次谐波滋生的现象，构建了厚度突变的阶梯板模型，研究了散射对累积二次谐波现象的影响。研究发现，阶梯板的存在对非线性兰姆波的传播存在两点影响：其一，厚度的改变会影响S0-S0 模式基波和二次谐波相速度的匹配程度，进而影响二次谐波的累积效应；其二，S0模式会在厚度突变处发生散射，且不发生模式转换。随着阶梯板的厚度差增大，这两种现象对于透射二次谐波的能量大小起到相反的作用，散射效应使得透射能量逐渐减小，但是厚度的减小使得二次谐波累积效应越来越明显，仿真结果中可以观察到透射二次谐波能量存在先上升后下降的趋势，在一定厚度差处存在一个极大值。而在均匀厚度板中，累积二次谐波的大小只与传播距离相关。综上，阶梯板中的非线性兰姆波存在两种能量转换机制，一是传播过程中基波能量向高次谐波馈入，二是阶梯板处的反射和透射。两种机制共同作用，决定了各个模态和频率的非线性兰姆波能量分配关系。