应用超声干涉特征识别微小缺陷

2022-03-05沙正骁曾甘露陆铭慧何方成陆传雨

应用声学 2022年1期

关键词：尾部幅值灰度

沙正骁曾甘露梁菁陆铭慧何方成陆传雨

(1 中国航发北京航空材料研究院北京 100095)

(2 南昌航空大学南昌 330063)

(3 航空材料检测与评价北京市重点实验室北京 100095)

(4 中国航空发动机集团材料检测与评价重点实验室北京 100095)

0 引言

随着金属材料制造水平的提高，航空飞行器中的合金材料性能提升巨大，同时质量验收标准也越发严格，材料内部允许存在的微小缺陷，如微夹杂、微气孔、微裂纹等的当量尺寸越来越小，这给无损检测带来了更大的挑战。超声检测是常用的无损检测方法，具有灵敏度高、高效、无污染等优点。但是传统超声脉冲反射法存在诸多限制，当待测工件厚度较大、缺陷微小时，缺陷的底波幅值低，极易使得小缺陷波信号湮没在噪声中。针对微小缺陷的超声识别遇到的困难，本文开展了以下研究：一是研究声波经过微小缺陷后的传播规律；二是改进和发展新的超声检测技术。

前人对于微小缺陷的超声检测进行了理论和实践研究。Rose 等[1]对超声波在金属材料内部的传播和散射作用进行了详细的推导。杨辰龙等[2]对含微小缺陷金属材料超声脉冲反射信号的成分进行分析，建立了基于散射声场与高斯底波理论的优化超声底波模型。Zhong等[3]通过对梁结构的振型数据使用小波变换和振型曲率的方法进行了微小缺陷识别。刘述煌[4]采用超声动态聚焦技术和时间反转自适应聚焦技术成功检测出φ0.4 mm 平底孔，信噪比可达6 dB 以上。林起本等[5]在Zhong 的研究成果基础上，提出了基于离散小波变换和移动质量法对板梁结构进行微小缺陷识别。王少军等[6]用超声散射法成功检测φ0.1 mm 的微小缺陷及埋藏深度1 mm 的近表面缺陷。唐晓明等[7]提出波形干涉法，利用管波和地层波干涉来调制阵列波数据。Pacheco 等[8]根据激励点和接收点位置，给出了散射波对散射介质特性、尾波观察时间等微小缺陷敏感性的解析式。张涛等[9]提出介质散射形成的尾波由于多次经过缺陷，比入射波更易发现介质的微小变化。赵元明等[10]简要介绍了尾波干涉理论，并搭建数值仿真平台，反演了微小缺陷的大小、形状和位置分布。

本文研究了入射波与微小缺陷散射波的干涉机理，利用有限元仿真方法对超声波经过微小缺陷时的声场变化以及波形变化进行了研究。设计制作了6 块铝合金微小缺陷试样，利用超声特征扫描成像系统对铝合金试样全面扫查，采集包含干涉特性的完整底波，进行底波尾部波列特征成像，成功检出所有预置的平底孔缺陷。

1 入射波与缺陷散射波的干涉理论

如在一球坐标系rθφ，θ= 0 是z轴，坐标原点存在一个半径为r的圆形小缺陷，一列沿z轴正方向传播的平面入射波入射到微小缺陷表面，并以缺陷为二级声源向四周辐射球面声波，球面波在缺陷周围叠加形成“散射波”[11]，微小缺陷的散射波声场表示为球面波的叠加。

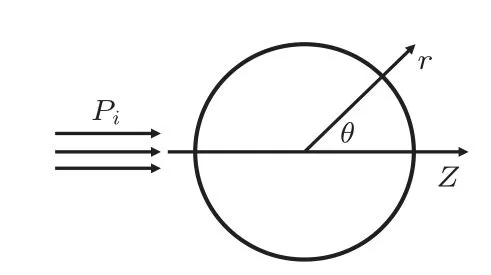
图1 圆形小缺陷处的散射Fig.1 Scattering from small circular defects

入射平面波可以写成

式(1)中，k为波数。

散射波为Pr，总声场为P=Pi+Pr。在球坐标系下，入射波展开为多个球函数的级数，表示为

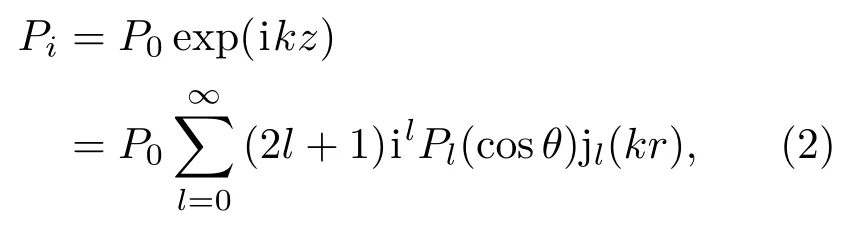
式(2)中，l为球函数的阶数，P0～Pl为球函数0～l阶的声压，jl为l阶贝塞尔函数。

散射波公式为

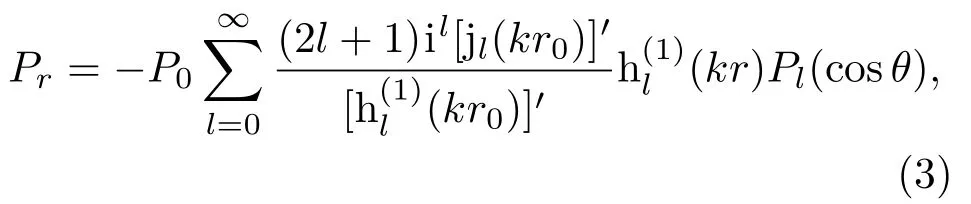
式(3)中，hl为l阶球汉克函数。

其远场解为

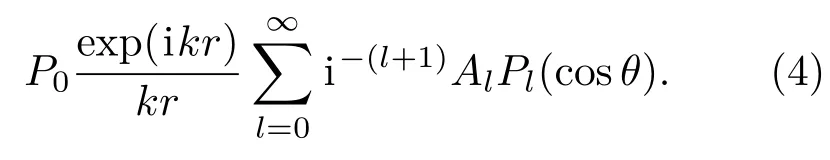
因远场具有平面波的性质，远场散射波声强可以写成

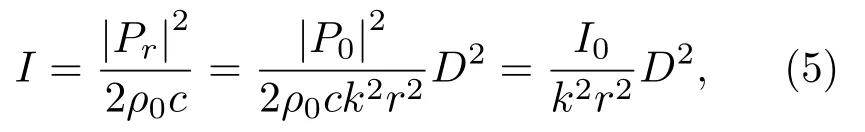
式(5)中，I0=|P0|2/(2ρ0c)是入射波声强，D是散射波的指向性，为待定系数。

以原点为中心，在近似球面的小缺陷上对上述声强公式积分，得到总散射功率：

当频率很低、kr0很小时，散射总功率很小，与(kr0)4成正比[12]。这个结论对其他形状的散射物也适用。频率增加，散射总功率增大，高频时趋于缺陷截面积入射功率的两倍。所以为了加大散射总功率，在满足反射波能量要求和控制衰减的前提下，应当适当加大超声探头的发射频率。

当kr0≪1时，可得平均散射功率的近似式为

当kr0≫1时，有

当入射波频率很小或者微小缺陷尺寸很小时，平均散射功率对比平均入射功率占比很小[13]，随着频率和微小缺陷尺寸的减小，平均散射功率呈指数形式下降。这结果表明，在微小缺陷识别时，当超声激励频率过低、超声波长远大于微小缺陷尺寸时，微小缺陷对入射波的影响较小，大部分入射波会直接绕过缺陷向前传播。当发射频率较高、入射波波长较短时，散射波将分成两部分[14]，一部分跟随入射波前进，作为一种相干波与入射波发生干涉作用增强或者减弱，另一部分改变方向，向与入射波相反的方向传播。

2 仿真研究

2.1 仿真参数设置

为了研究超声波在微小缺陷处的干涉现象，本文利用有限元仿真软件对内部含有微小缺陷的试样进行了仿真。其中，试样的尺寸为40 mm×20 mm，缺陷埋深为30 mm。此外，为确定缺陷尺寸对干涉现象的影响，本文分别设置了4 种对比试样并对其进行编号，它们分别为1 号试样，无缺陷；2 号试样，内部含有尺寸为0.1 mm×1.6 mm 的微小缺陷；3 号试样，内部含有尺寸为0.2 mm×1.6 mm 的微小缺陷；4 号试样，内部含有尺寸为0.3 mm×1.6 mm 的微小缺陷。接着，在软件材料库中将母材属性设置为7075 铝合金，缺陷属性设置为空气。试样的设计如图2所示。

图2 仿真试样Fig.2 Sample model

为了模拟超声波在真实试样中的传播情况，本文将试样的下边界设置为自由边界，以观察声波在底面的反射情况。同时，为了防止侧壁中的反射底波对接收波形的干扰，将其设置为低反射边界。其中，自由边界就如同介质的边界一样，对声波具有全反射作用。而低反射边界则更类似于吸收层，对声波具有吸收效果。

为保证仿真结果的准确性，通常，仿真中的最大网格尺寸应小于声波波长的1/5。在本文中，由于超声探头的激励频率为10 MHz，超声波在7075 铝合金中的声速为6300 m/s，因此，设置网格尺寸为0.1 mm。在上边界的指定位置处设置激励源，其中，激励源的波形为高斯调制的余弦波函数。其表达式如下：

式(8)中，f为激励信号频率，t为信号传播时间，激励信号的波形图如图3所示。

图3 激励信号图Fig.3 Excitation signal diagram

对于厚度为40 mm的铝合金试样，超声波在介质中的往返时间约为12.7 µs。为了获得完整底波信息，设置求解时间为16µs。在距试样上表面0.5 mm处设置一维截线，用于超声信号接收。

2.2 仿真结果

根据上文中参数进行有限元仿真，获得的瞬态应力云图如图4所示。图中色标表示介质中不同位置处的声波能量，显然，由多条红绿色长带构成的条纹是超声脉冲信号。

图4中的4 幅图分别描绘了超声脉冲信号在传播至φ0.1 mm微小缺陷前后的声场分布情况。可以看出，入射波传播至φ0.1 mm 缺陷时，大部分波绕过微小缺陷继续向前传播。同时，由惠更斯-菲涅耳原理可知，入射波作用于微小缺陷上，使其成为了一个二级声源，产生了向四周传播的球面散射波。由于微小缺陷产生的散射波与入射波相位相反，因此，散射波会与入射波产生干涉相消现象，具体过程如图4(b)～(d)中红色方框内所示。

由于散射波对入射波尾部的干涉现象，入射波尾部波列产生了畸变，因此可以通过入射波的尾部波列来表征散射波与入射波的干涉情况。此外，对比图4(c)和图4(d)可看出，随着声波传播距离增大，声波能量持续衰减，干涉作用效果减弱。各试样在一维截线处接收的信号时域波形如图5所示。

图4 2 号试样内部瞬态应力图Fig.4 Internal transient stress diagram of No.2 sample

图5(a)为16 µs内接收到的完整波形图，图5(b)为接收到的底波尾部波列(图5(a)中黑色框线框选中位置)的波形放大图。由图5(b)中可看出，无缺陷试样底波尾部波形较为平滑，而另外3 种缺陷试样的底波尾波受散射波干涉的影响，尾部波列的波峰幅值都发生了变化。通过对图5(b)中框选的波形进行分析，得到在t= 13.6 µs 时，1 号试样接收到的底波尾部波峰幅值为157.4 µm；而2 号、3 号、4 号有缺陷试样接收到的底波尾部波峰幅值依次降低0.42 µm、1.25 µm、3.14 µm。这一结果表明，散射波干涉作用会引起底波尾部波列幅值变化，且变化幅度与缺陷尺寸相关，缺陷尺寸越大，幅值变化越大。

图5 一维截线处的信号时域波形Fig.5 Time-domain waveform at the receiving end

仿真结果表明，超声波经过微小缺陷时会发生散射波与入射波的干涉现象，导致底波尾部波列幅值降低，说明以底波尾部波列作为特征参量对材料内部存在的微小缺陷进行成像识别是可行的。

3 超声特征扫描成像实验

3.1 试样设计制作

7075 铝合金具有良好的声学性能和深度钻孔性能。因此，本文利用其设计并制作了小厚度和大厚度的缺陷试样各3 块。小厚度试样用于测试干涉法对于近表面微小缺陷的检测能力，其厚度分别为5 mm、10 mm、20 mm。大厚度试样则用于测试干涉法对试样中埋深较大的微小缺陷的检测能力，其厚度分别为40 mm、60 mm、80 mm。值得注意的是，在大厚度试样中，厚度为40 mm和80 mm 的试样为圆柱体设计，其余试样为长方体设计。试样缺陷分布如图6所示。具体参数如表1所示。

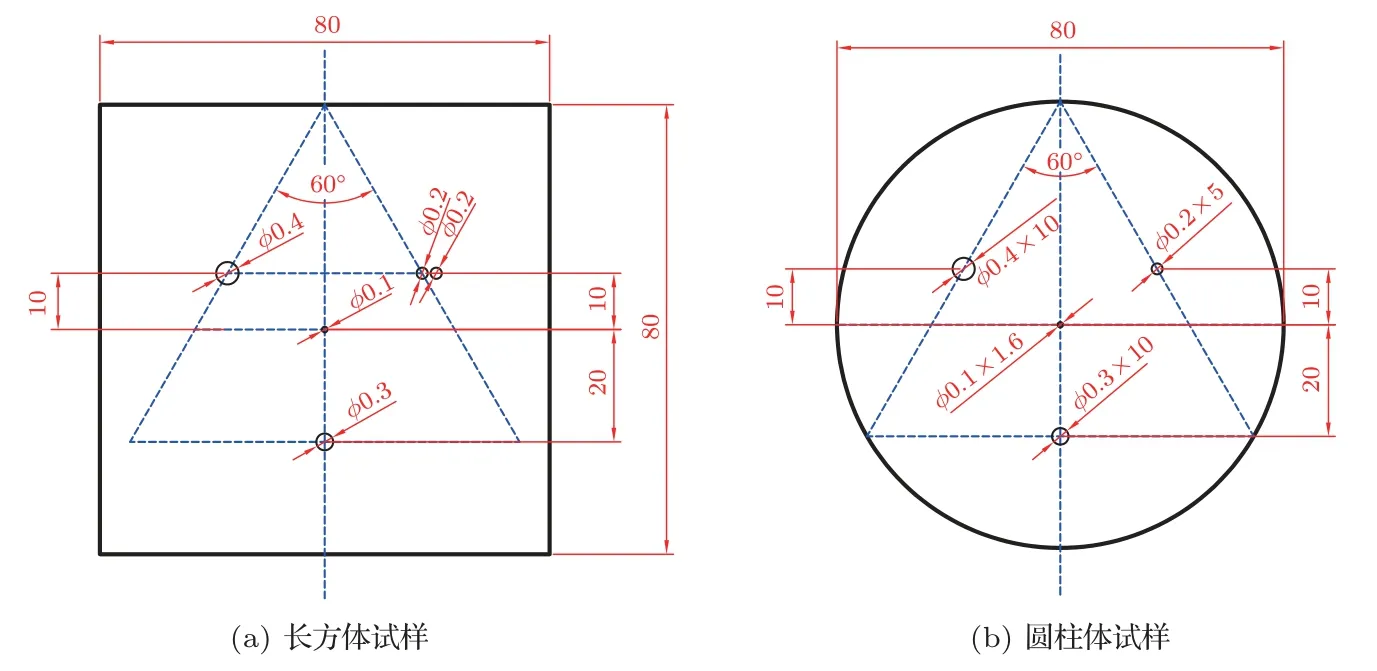
图6 试样缺陷分布设计图(单位: mm)Fig.6 Defect distribution design diagram of sample(Unit: mm)

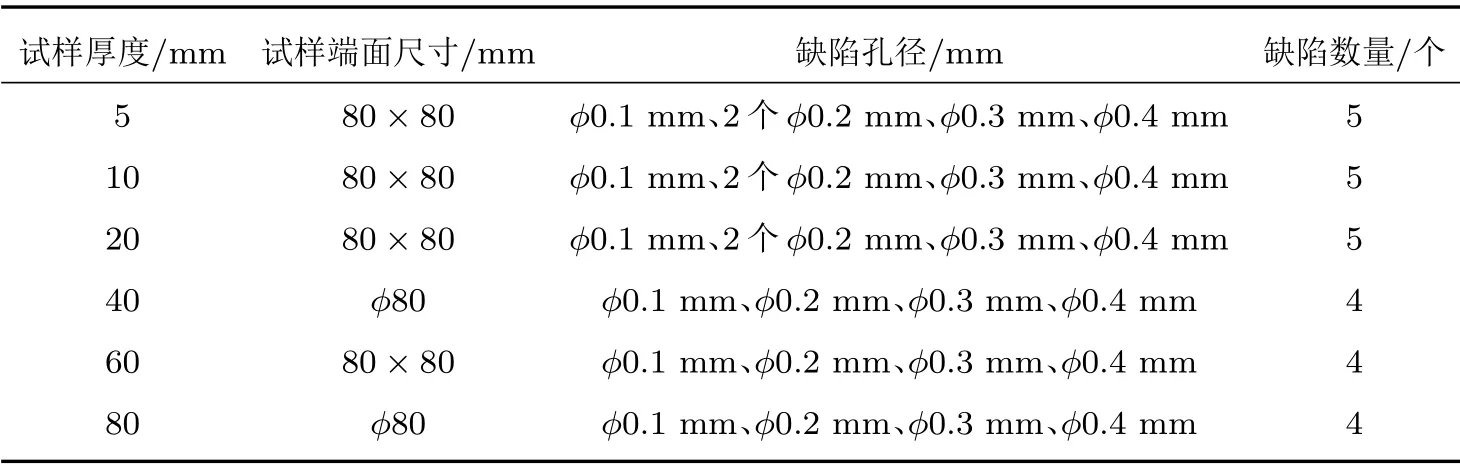
表1 试样具体参数Table 1 specific parameters of sample

3.2 特征扫描成像实验

本文采用超声特征扫描成像系统(F-scan)对上述试样进行检测。该系统的优势在于全波列采集完整的超声回波，并根据有无缺陷处的波形特征差异进行成像。实验采用5077超声发射接收仪进行信号发射和接收，探头选用频率为10 MHz 的水浸聚焦直探头。试样厚度为5～80 mm，跨度较大，为达到最佳检测效果，根据试样厚度的不同，使用了4个不同晶片尺寸和焦距的探头。探头参数如表2所示。

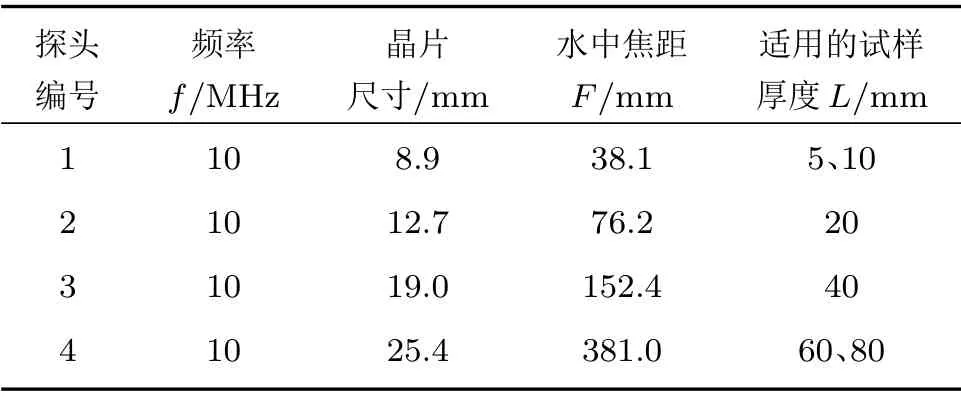
表2 探头具体参数Table 2 Specific parameters of probe

为了保证探头能量能聚焦到缺陷位置，获得较好的成像效果，需要计算水层厚度，计算公式为

式(9)中，L为试样的厚度，c2和c3分别为水和铝合金材料中的声速。

以5 mm厚度试样为例，具体实验步骤如下：将试样平整地摆放在超声水浸系统的水槽中，从表2可知，5 mm 厚度试样的检测应选择1 号探头，按公式(9)计算得到水层厚度为15.3 mm。打开超声脉冲发射接收仪，设置发射电压400 V 和激励频率10 MHz，同时调节增益使得底波尾部波列与噪声的信噪比达到最佳。扫查步进设为0.2 mm，扫查速度设为30 mm/s，为确保扫查范围覆盖整个试样，扫查范围设置为90 mm×90 mm。扫查完成后，框选底波尾部波列进行成像。

3.3 成像结果与分析

小厚度试样灰度成像如图7所示。从图7(a)～(c)可看出，试样中的无缺陷区域灰度值较低，底波尾部波列幅值较高；而有缺陷区域，灰度值较高，底波尾部波列幅值较低；由灰度差异构成的图像将孔径为φ0.1 mm～φ0.4 mm 的微小缺陷显现出来，且随着试样厚度增大，缺陷图像有被放大的趋势；5 mm 试样中的两个相距1 mm、φ0.2 mm 缺陷可以清晰分辨，而10 mm、20 mm试样中相距1 mm的φ0.2 mm 缺陷图像发生重叠，无法清晰分辨。因此，以底波尾部波列为特征参量进行成像，能够有效检出不同埋深的近表面缺陷，且当缺陷埋深小于5 mm 时，能够有效分辨相距1 mm、φ0.2 mm 的相邻平底孔微缺陷。

图7 小厚度试样灰度成像图Fig.7 The gray scale image of small thickness sample

大厚度试样灰度成像如图8所示。从图8可以看出，与小厚度试样相比，大厚度试样成像效果更差，因此将整体成像灰度值调高，从而提高对比度，使缺陷显示更清晰。试样厚度较大时，侧壁干涉会引起试样侧壁附近的底波尾部波列幅值降低，灰度值变大，调高整体成像灰度值后，侧壁附近部分影像缺失。由于缺陷位置不在侧壁附近，受侧壁干涉的影响小，不会影响检测结果。由图8可知，大厚度试样中孔径为φ0.1 mm～φ0.4 mm 的微小缺陷均可用干涉成像法检出，随着试样厚度增大，缺陷的放大作用更加明显，且缺陷周围出现明显的干涉条纹。分析认为产生缺陷放大现象的原因有二：一是大厚度试样检测使用的探头晶片尺寸较大，对微小缺陷有放大作用；二是散射波与底波尾部波列的干涉作用引起微小缺陷图像的放大，且随着厚度增大，超声波的扩散作用使得缺陷的放大得到加强。

图8 大厚度试样灰度成像图Fig.8 The gray scale image of big thickness sample

本文选择5 mm 试样的时域波形图分析近表面缺陷对底波尾部波列的影响，选择80 mm 试样的时域波形图分析大厚度工件中埋深较大的微缺陷对底波尾部波列的影响。80 mm 试样的厚度较大，全波列采集界面波至一次底波的完整波形会造成底波波列压缩，导致底波尾部波列无法被框选，故只采集底波尾部波列。5 mm 和80 mm 试样的时域波形如图9所示。

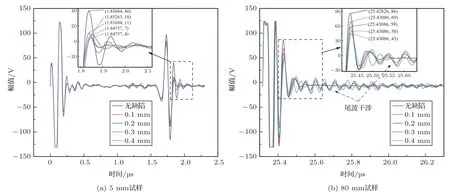
图9 时域波形图Fig.9 Time domain waveform

从图9可看出，5 mm和80 mm试样中的φ0.1 mm～φ0.4 mm 缺陷处的底波尾部波列幅值对比无缺陷处有所下降，且80 mm 试样的底波尾部波列下降幅度更小，原因是随着试样厚度增大，散射波的衰减增大，散射波干涉作用减弱，所以大厚度试样的底波尾部波列下降幅度更小。对比φ0.1 mm～φ0.4 mm 缺陷处的底波尾部波列幅值可知，底波尾部波列幅值大体上随缺陷尺寸的增大而减小，这一结果与仿真结果相符。从图9(b)可看出，无缺陷处的底波尾部较为平滑，而有缺陷处的底波尾部存在明显的“尾波干涉”现象，加剧了底波尾部的波形震荡，这一现象佐证了散射波干涉理论的准确性。