基于Polar码的水声通信信源信道联合译码方法
2022-03-05胡承昊台玉朋胡治国王海斌
胡承昊 台玉朋 汪 俊 胡治国 王海斌
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
随着人类海洋活动的日益增多,水声通信技术也受到越来越广泛的关注。一般来说,水声通信的可用带宽较窄,通信速率受限。同时,信道复杂、环境噪声高等特点也使水声通信提升可靠性较为困难。因此,如何在不降低通信速率的情况下提高系统可靠性一直是水声通信研究中的重要问题。传统水声通信系统中,信源译码和信道译码是分别独立设计的。然而,水声通信实际发送的信源符号之间通常具有相关性,这种相关性导致的信源冗余难以依靠传统信源编码压缩。此时,传统分离译码的方式会造成一定程度的带宽浪费。如果能够利用这部分残留冗余抵抗信道差错,则可进一步提高水声通信系统的可靠性。
早在20 世纪70年代便有学者在无线电通信领域提出利用信源残留冗余抵抗信道差错的思想[1]。1991年,Sayood 等[2]将信源建模为一阶马尔科夫模型,在信源编码网格图上进行信源译码,构建了早期的信源信道联合译码(Joint source-channel decoding, JSCD)方法。随后,Demir 等[3]和Park等[4]分别提出了符号约束和比特约束的信源编码网格图。在此基础上,文献[5–7]将信源译码与卷积码译码相结合,利用卷积码的纠错能力进一步提高通信系统的可靠性。随着Turbo码[8]和LDPC码[9]等近香农限信道编码的广泛应用,与之对应的JSCD 方法也得到大量研究。文献[10–12]研究了基于Turbo 码的JSCD 方法。文献[13–15]对基于LDPC 码的JSCD 方法展开了研究。研究表明,JSCD 方法能够在不降低通信速率的情况下提高系统可靠性。相比于无线电通信,水声通信提升通信速率和可靠性更为困难,因此在水声通信中研究JSCD方法有重要意义。但是,目前关于JSCD方法的研究主要集中在无线电通信领域,在水声通信中的研究较少。
受通信速率的限制以及信道时变等因素的影响,水声通信中的码块长度通常较短。目前,水声通信中常用的Turbo 码和LDPC 码等信道编码的短码性能并不理想。并且这类采用迭代译码方式的信道编码在信噪比达到一定值后,其误码率下降非常缓慢,即会出现所谓的“ 差错平台”效应。2009年,Arikan 等[16−17]提出了一种新的信道编码方法––Polar 码。该编码方法利用信道极化原理进行编译码,在理论上达到了香农极限。目前,Polar 码已被采纳为5G 通信协议中的编码标准之一。研究表明,相比Turbo 码和LDPC 码,Polar 码能够取得更好的短码性能[18−19],并且在较高信噪比下仍未观察到“ 差错平台”效应[20]。因此,本文考虑将Polar码应用于水声通信,并研究与其对应的JSCD方法,进一步提高水声通信系统可靠性。
不同于Turbo 码和LDPC 码,Polar 码采用了全新的编码结构,其常用的顺序消去列表译码(Successive cancellation list, SCL)[19]方法在计算软信息时利用了前序信息序列的判决结果,导致其软信息绝对值较大。若采用迭代的形式实现联合译码,容易放大信道译码的差错,降低译码性能[21]。这导致传统针对Turbo码和LDPC码提出的JSCD 方法无法直接应用于Polar 码。近年来,关于Polar码JSCD 方法的研究少有突破。2016年,Wang 等[22]在无线电通信中对Polar 码的JSCD 方法进行了初步尝试。该方法根据自然语言规则构建信源字典,在Polar码译码过程中利用信源字典对译码进行修正,在自然语言传输条件下,取得了优于传统分离译码(Separate source-channel decoding, SSCD)的性能。然而,该方法中的信源译码和信道译码在两个译码树上分别进行,译码的一体化程度有待进一步提高。另外,在传输语声和图像等信息的情况下,该方法难以利用信源符号间相关性导致的残留冗余抵抗信道差错。
本文根据Polar 码的译码结构,提出了一种基于Polar 码的水声通信信源信道联合译码(Polar codes based joint source-channel decoding, PJSCD)方法。在译码过程中综合信源转移概率和信道转移概率计算统一的序列后验概率,最终选择后验概率最大的信源序列作为译码结果。所提方法以信源状态转移关系为基础构建信源信道联合译码网格图,该联合网格图能够同时描述信源状态转移关系和信道状态转移关系,从而实现信源译码和信道译码的一体化联合优化,利用信源符号间相关性导致的残留冗余抵抗信道差错,在不降低通信速率的情况下提高水声通信系统可靠性。
1 Polar码基本原理
本节将简要介绍Polar 码的基本原理。在下文的论述中,采用xji表示向量(xi,xi+1,···,xj),当i>j时则表示空向量。
Polar 码的核心理论即信道极化。信道极化主要包括信道合并和信道分离两个过程,其中,信道合并对应着编码过程,信道分离对应着译码过程。假设待编码序列为uN1,则Polar码的码字可表示为xN1=uN1GN,其中,码长N= 2n, n= 1,2,···。生成矩阵GN=BNF⊗n,其中,BN为比特倒序置换矩阵,F⊗n表示的n次Kronecker幂。至此,将N个独立信道合并为了一个N阶合成信道其中,W(yi|xi)对应着实际的物理信道,表示发送xi接收到yi的概率。通过定义式(1)所示的子信道,可以将N阶合成信道分离为N个子信道。

译码方面,SCL 译码[19]是目前Polar码应用最广泛的译码方法之一。该方法逐信息比特地构建译码树搜索可能的信息序列,最终选择可靠性最高的作为译码结果。在译码树的扩展过程中,SCL 译码器每次仅保留最可靠的L条路径向下译码,以此达到降低算法复杂度的目的。文献[25]在假设各信息比特发送概率均为0.5 的情况下推导了Polar 码序列后验概率表达式,利用序列后验概率作为可靠性的度量,进一步提高了SCL译码的性能。
2 基于Polar码的信源信道联合译码方法
2.1 所提方法的通信系统模型
图1为所提方法的通信系统模型。发送端,长度为D的信源序列sD1经信源编码得到长度为K的信息序列cK1,信息序列经Polar 码编码得到长度为N的码字xN1,码字经交织和调制后发送至水声信道。接收端经过解调和均衡后得到接收序列yN1。信源信道联合译码器构建联合译码网格图,一方面,利用联合译码网格图中的信源状态转移关系和信源先验信息计算信源转移概率;另一方面,利用联合译码网格图中各译码路径所对应的信息序列和接收序列递归地计算各信息比特对数似然比,并在此基础上计算信道转移概率。将信源转移概率和信道转移概率按照一定规则合并可得各译码路径的序列后验概率。最终,选择后验概率最大的路径,将其对应的信源序列作为译码结果。

图1 所提方法的通信系统模型Fig.1 The transmission system
2.2 信源信道联合译码度量
将译码看作一个序列估计过程,采用最大后验概率准则译码,则译码结果可表示为

式(2)中:s′D1为一种可能的发送信源序列,cK1(s′D1)为对应的信息序列。由于待编码序列uN1(s′D1)和信息序列cK1(s′D1)是一一对应的, 因此有P(cK1(s′D1)|yN1)=P(uN1(s′D1)|yN1)。为方便表述,下文中采用uN1表示uN1(s′D1),则序列后验概率可表示为

当不考虑信源先验信息时,Polar 码的序列后验概率可表示为[25]

式(4)中:为第τ个子信道的对数似然比,Ki为ui1中包含的信息比特数。对比式(3)、式(4)可知实际的序列后验概率与PU(ui1|yN1)存在如下关系:

由于uN1与s′D1一一对应,因此有P(uN1)=P(s′D1)。为表示信源符号间的相关性,将其建模为马尔科夫模型,本文采用一阶马尔科夫模型进行说明,则有忽略常数2K,采用式(5)的对数形式作为译码度量,可表示为

一方面,由于Polar 码译码过程中使用了前序信息比特的判决结果,导致对数似然比的绝对值较大。为避免产生数值问题,同时降低算法复杂度,在计算对数似然比的过程中通常采用式(7)所示的近似。这使得信道转移度量的计算结果与真实值之间存在一定偏差。另一方面,由于水声信道的影响,导致来自信道信息的可信度相比高斯白噪声信道(Additive white gaussian noise, AWGN)降低。因此,在译码度量中加入参数α调节信源转移度量和信道转移度量在译码度量中所占比重。在本文的研究中,通过大量仿真选择使系统误码率最低的α作为经验参数,也可在实际应用中逐渐调节至最优值。一般来说,α的取值在一定范围内均可使译码性能接近最优。

2.3 基于联合译码网格图的译码方法
最大后验概率译码器搜索所有可能的信源序列并计算其对应的译码度量,最终选择译码度量最大的作为译码结果。为了更加高效地计算各信息序列的译码度量,以尽量低的算法复杂度实现接近最优的译码性能,构建信源信道联合译码网格图,在联合译码网格图上进行联合译码。
本文以信源状态转移关系为基础对Polar码译码树进行重组,构建信源信道联合译码网格图。图2为信源集合包含3 个符号时的一种联合译码网格图示例,其中,3个符号对应的信源编码分别为0、10和11。

图2 联合译码网格图示例Fig.2 An example of joint decoding trellis
图2中横轴为译码比特数,实线框表示译码节点,其内部数字为译码符号数,虚线框表示译码比特数相同且最后一个符号相同的译码节点集合,称之为集合节点。由根节点出发总是存在唯一的路径与网格图中的译码节点相连,称其为该译码节点所在的译码路径。在联合译码网格图中,译码节点之间的连线能够有效表示信源状态转移关系,从而为利用信源符号间相关性导致的残留冗余抵抗信道差错提供基础。同时,根据信源编码规则可以得到各路径对应的信息序列。因此,在联合译码网格图上能够同时进行信源译码和信道译码,在统一的网格图上实现信源译码和信道译码的一体化联合优化。
信源信道联合译码器从根节点出发,逐信息比特地构建联合译码网格图。对于网格图中的每个译码节点,根据其所在译码路径中的信源转移关系,可得与其对应的信源序列sD1′,其中,D′为当前译码节点对应的译码符号数。利用信源先验信息可得与之对应的信源转移度量:

式(8)中:M′source为当前译码节点母节点对应的信源转移度量。
另一方面,根据sD′所对应的信源编码cl1,可得当前译码节点对应的待编码序列片段ui1。结合接收符号序列yN1,利用Polar 码的编码结构可递归地计算当前译码节点对应的信道转移度量:

式(9)中:M′channel为当前译码节点母节点对应的信道转移度量,i为当前译码的信息比特数。对数似然比可采用式(10)、式(11)递归地计算[16]。

如果构建完整的联合译码网格图,搜索所有可能的信源序列,则算法复杂度为O(NlgN ·|S|D),其中,|S|为信源符号集合中包含的符号数量。算法复杂度随信息序列长度指数增长,难以实际应用。为了降低所提方法的复杂度,在译码过程中,对每个集合节点仅保留B个译码度量最大的译码节点继续向下译码,其余译码节点则被删除。当译码网格图进入稳态后,每译码一个信息比特,网格图中均包含|S|个集合节点,分别对应当前所有可能的信源符号。每个集合节点均包含B|S|个译码节点,分别对应前序译码节点所有可能的情况。因此,所提方法的复杂度为O(NlgN·B|S|2)。另外,对于译码网格图中的每一层,各译码度量增量的计算互不影响。因此,所提方法可以利用并行计算进一步提高运行效率。
3 仿真分析
3.1 仿真条件
为验证所提方法的有效性,利用数字图像处理中的标准测试图像––Lena 灰度图作为训练序列统计信源先验信息进行仿真,该灰度图如图3所示。首先,利用差分脉冲编码调制(Differential pulse code modulation, DPCM)对该灰度图进行编码。统计DPCM 编码结果中各符号的发送概率,并构建Huffman编码。经过DPCM 编码后,信源中仍然存在残留冗余[2]。为此,将信源建模为一阶马尔科夫模型,并统计各符号之间的一阶马尔科夫条件概率分布。将各符号的发送概率和一阶马尔科夫条件概率作为信源先验信息用于后续仿真。表1给出了各符号对应的发送概率和Huffman 编码。表2为条件概率分布P(Y|X)的统计结果。若利用R=(Y|X)表示信源冗余度,其中,为Huffman 编码的平均码长,H(Y|X)为信源的条件熵,则仿真所用信源的冗余度为0.494。

表1 各信源符号的发送概率和Huffman 编码Table 1 Transmission probability and Huffman codes of each source symbol

表2 信源符号条件概率分布Table 2 Conditional probability distribution of source symbols

图3 统计信源先验信息所用灰度图Fig.3 The grayscale image used to get source prior information
仿真过程中,按照信源先验信息随机地生成信源序列进行仿真。信息序列经码长N= 1024、码率R= 4/5 的Polar 码编码生成码字。Polar码采用高斯近似(Gaussian approximation, GA)法构造[24],构造参考比特信噪比为2.5 dB,冻结比特取值为0。码字经过二进制相移键控(Binary phase shift keying, BPSK)调制后发送至信道。
为了考察所提方法对系统可靠性的提升,接收端分别利用传统分离译码和所提方法进行译码。在所提方法中,令参数B= 4。对于传统分离译码方法,发送端采用与所提方法相同的方式发送通信信号。接收端,各比特对数似然比首先利用SCL 译码进行信道译码,再通过Huffman译码进行信源译码。仿真过程中令SCL译码的列表大小L=32。
3.2 仿真结果
首先在AWGN 信道下进行仿真。通过仿真选择使译码性能最优的参数α=1.5。图4为不同比特信噪比下传统分离译码方法和所提方法的误比特率(Bit error rate, BER)仿真结果。仿真结果显示,所提方法能够将系统BER 达到10−4所需比特信噪比由传统分离译码的4.16 dB 降低至3.16 dB,获得约1 dB 信噪比增益。可见,所提方法能够有效利用信源符号间相关性导致的残留冗余抵抗信道差错,在不降低通信速率的情况下提高系统可靠性。

图4 AWGN 信道下的仿真结果Fig.4 Simulation results in AWGN channel
文献[15]提出了一种基于LDPC 码的JSCD 方法,取得了优于传统分离译码的性能。为了对比该方法与所提方法的译码性能,在相同条件下对两种方法进行仿真,其中,LDPC 码采用渐进边增长(Progressive edge growth, PEG)算法构造[26],码长为1024,码率为4/5,仿真过程中令BP 译码器的迭代次数为10,联合译码器的迭代次数为5,其内部的译码参数α= 10。系统BER 和误帧率(Frame error rate, FER)的仿真结果分别如图5(a)、图5(b)所示。由仿真结果可见,当系统BER 达到10−4时,所提方法相比基于LDPC码的JSCD方法能够获得约0.34 dB 信噪比增益,当系统FER 达到10−3时,所提方法相比基于LDPC码的JSCD方法能够获得约0.50 dB信噪比增益。可见,所提方法在统一的译码网格图中实现信源译码和信道译码的一体化联合译码,有利于进一步提高通信系统的可靠性。

图5 所提方法与基于LDPC 的JSCD 方法BER与FER 仿真结果Fig.5 The BER and FER simulation results of the proposed algorithm and the JSCD based on LDPC codes
为验证所提方法在水声信道下的有效性,进一步在图6所示的实测时变水声信道下进行仿真。接收端采用判决反馈均衡器(Decision feedback equalization, DFE)对水声信道多途效应导致的码间串扰(Intersymbol interference, ISI)进行补偿,其中,自适应算法采用归一化最小均方算法,令前馈滤波器阶数为20,反馈滤波器阶数为65。通过仿真选择使译码性能最优的参数α= 4。图7为不同比特信噪比下传统分离译码和所提方法的BER仿真结果。

图6 仿真时域信道冲击响应Fig.6 Channel impulse response used in simulation

图7 实测水声信道下的仿真结果Fig.7 Simulation results in measured underwater acoustic channel
仿真结果显示,在复杂水声信道下,传统分离译码所需信噪比大幅提高,而所提方法的性能则更加稳定。此时,本文所提方法能够将系统BER 达到10−4所需比特信噪比由传统分离译码的18.5 dB降低至17.0 dB,获得约1.5 dB 信噪比增益,高于AWGN信道下的结果。在复杂时变水声信道下,受限于均衡器的性能,水声信道ISI 难以全部消除,即使信噪比很高,均衡器的输出结果中仍然存在一定干扰。相比之下,来自信源的信息不会受到复杂水声信道的影响。由于本文所提方法能够有效利用来自信源的信息抵抗信道差错,因此,在复杂水声信道下能够获得比传统分离译码方法更加稳定的译码性能,所取得的信噪比增益也比在AWGN信道下更高。可见,在水声通信中研究信源信道联合译码对提升水声通信系统的可靠性具有重要意义。
4 湖上实验
4.1 实验概述
为进一步验证所提方法在实际水声通信中的有效性,中国科学院声学研究所的相关工作人员于2020年12月在千岛湖开展了一次水声通信实验。实验采用单发单收模式,实验水域水深约为45 m。发射端通过在实验平台上吊放水声换能器的方式发射通信信号,吊放深度约为10 m。接收端利用摩托艇在预设通信距离处吊放水听器进行接收,接收深度约为15 m。实验期间的通信距离在200~4000 m之间。图8为实验整体示意图。
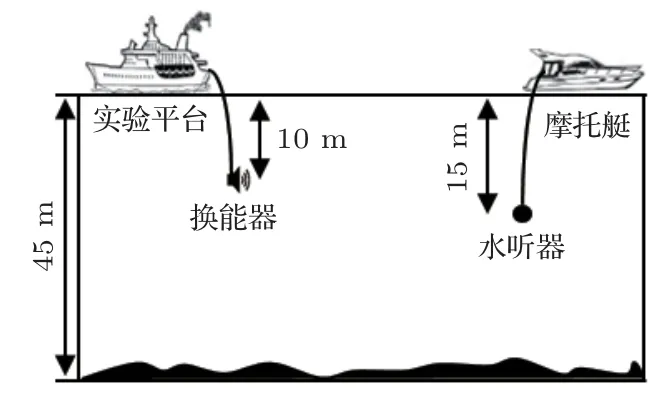
图8 实验示意图Fig.8 The experimental configuration
实验共发送两种类型的信号。第一种信号T1发送的信源为DPCM 图像编码序列。从USC-SIPI图像数据集中选取28张灰度图构建图像训练集。将训练集中的每张图像均拆分为若干个32×32 的子图,对每个子图分别进行DPCM编码并统计信源先验信息。取各子图信源先验信息的平均值用于后续的编译码。编码时,对图9所示的灰度图像以同样的方式进行DPCM编码,根据从训练集中获取的信源先验信息进行Huffman编码生成信息序列。第二种信号T2发送的信源为随机序列,采用与仿真相同的方式随机产生,其信源先验信息由图9统计得到。随机产生的信源序列经Huffman编码得到信息序列。

图9 实验发送的灰度图Fig.9 The grayscale image transmitted in the experiment
两种信息序列经过码长N= 1024、码率R=4/5的Polar码编码生成码字,其中,Polar码采用高斯近似法构造,构造参考比特信噪比为2.5 dB。码字经过交织后利用正交相移键控(Quadrature phase shift keying, QPSK)调制得到通信信号,并利用换能器发送,其中,发射中心频率为7.5 kHz,带宽为5 kHz,发送符号速率为2500 符号每秒,通信速率为4000 bit/s。在发射信号前端加入长度为600 bit的训练序列用于DFE抽头系数的训练阶段,分别占两种信号发送信息总数的1.5%和0.7%。
接收端,接收信号经过解调后利用DFE补偿水声信道ISI,采用递归最小二乘算法作为DFE 中的自适应算法。作为对比,对均衡后的结果分别利用传统分离译码和本文所提方法进行译码。在所提方法的译码过程中,令参数B= 4、α= 1.5。在分离译码过程中,令SCL 译码的列表大小L= 32。当传输图像序列时,译码结果再经过DPCM译码恢复出图像。
4.2 实验结果
为了更加清晰地展示发送图像序列时所提方法的性能,以通信距离277 m 处的接收信号为例进行分析,该信号对应的信号类型为T1。图10(a)、图10(b)分别展示了该接收信号的时变信道冲击响应估计结果和瞬时信道冲击响应估计结果。可见,该信号对应的信道响应长度可达50 个符号间隔以上,且存在时变性。在均衡过程中,令前馈滤波器阶数为80,反馈滤波器阶数为60,遗忘因子λ=0.998。图11(a)、图11(b)分别为传统分离译码和所提方法译码所恢复的图像,其对应的误比特率分别为2.7×10−2和0。此时,由于误码的产生,传统分离译码恢复的图像中存在大量噪点,而所提方法能够完整地恢复原始图像。

图10 实测信道冲击响应Fig.10 Measured channel impulse response

图11 译码结果Fig.11 Decoding results
对通信距离200~4000 m 处接收信号的误比特率进行统计,结果如表3所示。对于信号T1,所提方法在所有通信距离上实现了无误码通信,而传统分离译码方法的BER 仍然为3.7×10−3。对于信号T2,所提方法可将系统BER由传统分离译码方法的1.9×10−2降低至4.0×10−4,降幅可达一个数量级以上。可见,所提方法能够有效利用信源符号间相关性导致的残留冗余抵抗信道差错,在不降低通信速率的情况下提高水声通信系统可靠性。

表3 实测误比特率Table 3 Measured bit error rate
5 结论
本文根据Polar 码的译码结构提出了一种基于Polar 码的水声通信信源信道联合译码方法。该方法以信源状态转移关系为基础构建信源信道联合译码网格图,在联合译码网格图上同时进行信源译码和信道译码,综合信源转移概率和信道转移概率计算统一的后验概率,实现了信源译码和信道译码的一体化联合优化。仿真结果表明,所提方法能够利用信源残留冗余抵抗信道差错,在不降低通信速率的情况下,取得优于传统分离译码的误码率性能,并且在复杂水声信道下,所提方法能够取得比在AWGN 信道下更高的信噪比增益。湖上实验结果显示,所提方法能够将系统误码率由传统分离译码的1.9×10−2降低为4.0×10−4。当传输图像序列时,所提方法对全部接收信号均实现了无误码通信,而传统分离译码的误码率仍然为3.7×10−3。
在后续的研究当中,一方面,考虑继续细化分析译码参数α对译码性能的影响,研究效率和精度更高的参数选取方法,进一步提高水声通信系统的可靠性;另一方面,进一步优化信源先验信息的提取方法,提高信源符号间相关性的利用效率。
