非圆化磨耗激励下高速列车转向架区域噪声边频带产生机理及影响∗
2022-03-05高东璇
王 韬 高东璇 肖 健
(四川工程职业技术学院 德阳 618000)
0 引言
我国高速铁路技术不断发展,列车运行速度和运量不断提高,这极大地提高了我国国民的出行效率。然而,伴随而来的噪声问题也越发突出和明显。因此,高速列车的减振降噪一直以来都是研究热点。大量研究表明,轮轨表面的各类不平顺是高速列车噪声的主要根源[1]。其中,车轮非圆化磨耗作为一种常见的车轮表面异常磨耗,广泛地存在于我国的多类高速列车上。非圆化磨耗又被称为多边形磨耗,其特征表现为车轮半径沿着圆周方向呈周期性的变化,因此车轮在滚动的过程中会显著提高轮轨相互作用力,从而产生严重的轮轨异常振动和噪声,这对列车的安全性和乘客的乘坐舒适性带来了十分不利的影响[1−3]。
近年来,因车轮非圆化磨耗而导致的高速列车异常噪声问题时有发生,这引起了行业内相关技术人员的广泛关注。王兴宇等[4]采用阶次分析的方法,对列车运行时的车内噪声数据进行分析研究,从实验的角度阐述了车轮非圆化磨耗阶次和车内噪声主频之间的联系,即当列车运行速度和车轮直径给定时,车内噪声的主频和非圆化磨耗阶次存在一一对应的关系。在文献[4]的研究基础上,韩光旭等[5−6]扩大了实验样本数目和实验周期,针对我国某线路上的不同型号的动车组列车开展为期2年的振动、噪声和车轮非圆化磨耗跟踪测试,研究不同运营里程下的车辆振动噪声特性,并和车轮非圆化磨耗测试结果进行同步分析,研究车辆振动噪声和车轮非圆化磨耗之间的相互关系,除了得到和文献[4]类似的结论以外,还探明了车辆振动噪声水平和车轮非圆化磨耗幅值的之间的定性规律,即非圆化磨耗幅值越大,车辆振动噪声水平也越大。上述研究均集中在实验研究范畴,还未对机理开展深入研究。在上述研究的基础上,Zhang 等[7]针对非圆化磨耗产生的车辆噪声问题,开展了十分详尽的综合性研究,结合实验研究和仿真计算,初步分析了高速列车车轮非圆化磨耗状态对车内噪声的影响。建立了车内噪声预测模型,探明了车轮非圆化参数、车轮径跳和车内噪声之间的关系。其中,车内噪声预测模型主要分为两部分,首先是基于TWINS 轮轨噪声原理建立的轮轨噪声预测模型,以此模型计算所得的轮轨噪声为输入信号,输入到基于混合有限元-统计能量法的车内噪声预测模型[8]之中,最终可以计算得到车内噪声响应。此模型在一定程度上能够作为分析非圆化磨耗对车辆噪声影响的重要理论工具,然而当考虑更加复杂的移动条件下的轮轨耦合作用问题时,基于TWINS 轮轨噪声理论的轮轨噪声预测模型还不能满足研究需求,需要对模型进行完善。
总体上来说,通过大量的实验研究和理论分析,人们对车轮非圆化磨耗引起的车辆噪声问题已经有了一定程度的认识,得到的普遍结论是车轮非圆化磨耗会使得车辆噪声在非圆化磨耗激励频率处产生噪声峰值,从而显著增加车辆噪声水平。然而,本文作者团队在轮轨噪声测试中发现转向架区域噪声窄带频谱上出现了以非圆化磨耗激励频率为中心,等间距分布的噪声峰值,此现象和齿轮传动系统中的振动信号调制边频带类似[9−10]。这使得车轮非圆化磨耗不仅会影响其激励频率处的噪声,还会对其他频段的噪声产生重要影响。通过进一步分析,认为这是运行过程中,带有非圆化磨耗的车轮和轮轨系统的高频柔性特性耦合作用导致的。但是由于基于TWINS 理论的轮轨噪声预测模型无法考虑更加复杂的移动条件下的轮轨耦合作用问题,故还未见有文献对轮轨噪声边频带的产生机理进行理论研究。因此,本文针对非圆化磨耗激励下,转向架区域噪声频谱图上出现边频带这一现象,通过理论分析,探明其产生机理。并建立基于车辆-轨道刚柔耦合系统动力学模型和TWINS 轮轨噪声理论相结合的轮轨噪声预测模型,通过仿真再现轮轨噪声边频带这一现象,并对其影响因素开展研究。
1 转向架区域噪声特性实验研究
为测试高速列车运行时的转向架区域噪声,在转向架端部靠近车轮位置布置噪声传感器,如图1所示,同时,在车下安装GPS,并和噪声传感器用同一数采前端进行数据采集,保证列车速度、经纬度等信息和轮轨噪声信号具有同步性,便于后期的数据分析。另外,在进行噪声跟踪测试的同时,对相应车轮的表面状态也开展同步的跟踪测试。为了消除钢轨表面不平顺对测试的影响,在实验开始的时候对列车运行区间的钢轨进行打磨。测试车辆为拖车,无牵引电机和齿轮箱等动力装置。车辆运行速度约为300 km/h。

图1 噪声测点及传感器Fig.1 Noise test site and sensor
图2(a)给出了不同镟后里程下,转向架区域噪声的1/3 倍频程谱图。由图可知,刚进行完车轮镟修后,转向架区域噪声无明显显著的频段。而当运行里程提高至镟后6×104km 时,630 Hz 频段的噪声水平不断增加,并逐渐成为了主频。随着运行里程进一步提高,转向架区域噪声主频由630 Hz频段扩展至400~1000 Hz 频段。噪声主频变宽会增加噪声控制成本,因此需要重视此问题。为了对转向架区域噪声特性开展进一步研究,图2(b)给出了转向架区域噪声的快速傅里叶变换(Fast Fourier transform, FFT)谱图。由图可知,转向架区域噪声主要存在132 Hz、453 Hz、584 Hz、715 Hz和845 Hz频率峰值。其中132 Hz 是列车以300 km/h 速度运行通过0.625 m 间距的轨枕导致的,峰值大小不随运行里程改变。而453 Hz、584 Hz、715 Hz和845 Hz噪声峰值大小随着运行里程增加而不断增大。另外,还应当注意到,上述4 个噪声峰值为等间距分布,其频率间隔为130~132 Hz。
为了研究上述转向架区域噪声频谱中等间距分布的峰值来源,需要对转向架区域噪声成分展开讨论。一般情况下,转向架区域噪声主要包括轮轨噪声和气动噪声这两部分。对于气动噪声,其噪声频谱较宽,且往往不具有随运行里程增加而增加的特性。而对于轮轨噪声,主要是轮轨间相互作用导致的,受轮轨表面粗糙度影响。列车运行里程不断增加,车轮表面状态也随之恶化,这会导致其辐射噪声增大。显然,图2的转向架区域噪声测试结果和轮轨噪声的变化规律更接近。为了进一步探明转向架区域噪声峰值和轮轨噪声的关系,需要结合轮对轴箱的振动加速度进行分析。由于轮轨噪声是由轮轨激励引起的,那么轮对轴箱的振动特性可以在一定程度上表征轮轨噪声的特性。图3给出了车轮镟修后运行17×104km 时的轮对轴箱振动加速度频谱特性,并和相同镟后运行里程下的转向架区域噪声频谱进行对比。由图可知,转向架区域噪声频谱和轴箱振动频谱特征十分相似,且振动噪声的峰值也都能一一对应,故认为转向架区域噪声峰值主要来源于轮轨相互作用。

图2 轮轨噪声频谱特性Fig.2 Noise spectrum of wheel-rail noise

图3 振动噪声频谱特性对比Fig.3 Spectrum of the sound pressure level of bogie region and the acceleration of axlebox
影响轮轨噪声的主要因素为轮轨表面粗糙度水平,由于在测试之前,对运行区间的钢轨进行了打磨,所以认为钢轨表面状态良好,故需要重点关注车轮的表面状态。图4给出了不同镟后运行里程下的车轮非圆化磨耗测试结果,图中横坐标为阶次,纵坐标为粗糙度水平。由图可知,刚进行完镟修后,车轮表面状态良好。但是随着运行里程的提高,车轮的18 阶非圆化磨耗迅速发展,当镟后里程达到18×104km时,车轮的18阶非圆化磨耗的粗糙度水平接近30 dB,这表示车轮每转动一圈,会产生18次轮轨冲击。此测试车轮除了存在18 阶非圆化磨耗以外,无其他明显的高阶非圆化磨耗。因此,当列车运行速度为300~305 km/h、车轮直径约为0.83 m时,通过式(1)可以计算其激励频率:

图4 车轮表面粗糙度Fig.4 Surface roughness of the wheel

式(1)中,f为车轮非圆化磨耗的激励频率,v为列车运行速度,D为车轮直径。通过计算可知车轮非圆化磨耗的激励频率为575~585 Hz。按照普遍关于车轮非圆化磨耗引起的车辆噪声问题的相关结论[4−7],此车轮会产生575~585 Hz 的轮轨噪声,并且随着运行里程的增加,此频率处的噪声幅值也随之增加。因此,可以认为在转向架区域噪声频谱中584 Hz 频率峰值是由车轮非圆化磨耗激励导致的。
最后,应当注意到转向架区域噪声峰值具有等间距分布的特征,这是一种在齿轮传动系中较为常见的异常信号问题,称之为信号边频带。各个轮轨噪声峰值间隔约为130~132 Hz,恰好在噪声频谱上存在131 Hz 的峰值,这是列车以300 km/h的速度运行于轨枕间距为0.625 m 的线路上而产生的过轨枕冲击导致的。因此,初步推测导致非圆化磨耗激励频率两侧出现轮轨噪声边频带的原因或许和过轨枕冲击有关。为了进一步开展转向架区域噪声边频带产生机理的研究,需要借助理论计算。
2 轮轨噪声边频带产生机理
2.1 轮轨耦合作用理论模型
为探明轮轨噪声在多边形磨耗激励频率两侧出现的等间距的边频带是否和过轨枕冲击有关,需要建立轮轨耦合系统动力学模型进行理论分析。一般情况下,轮轨耦合系统可以简化为如图5所示的动力学分析模型,认为车轮和钢轨之间由一个Hertz非线性弹簧连接。

图5 轮轨耦合系统动力学模型Fig.5 Dynamics model of wheel-rail coupling system
图5中,Zw为车轮的位移,Zr为钢轨的位移,Zoor为因轮轨接触面不平顺而引起的位移,在此文中主要为车轮多边形磨耗导致的位移。其动力学方程可以表示为

式(2)中,M为等效质量;C为等效阻尼;K0为Hertz弹簧静刚度;K1为Hertz 弹簧动刚度,当车轮存在多边形磨耗时,Hertz 弹簧动刚度受多边形磨耗激励主导;Z(t)则为轮轨间的刚性位移量;Zs(t)则为钢轨的弯曲变形量,其频率为过轨枕频率。
方程右边可以理解为多边形磨耗激励下系统的外力输入,第一部分记为Fs1(t),其表达式为式(3),表示和钢轨的弯曲变形相关的惯性激励力、阻尼激励力和弹性激励力对系统共同作用的结果;Fs1(t)的傅里叶变换为F′s1(f),表达式见式(4)。Fs1(t)产生的响应信号频率包含了过轨枕频率fs及其二倍频,如图6(a)所示。
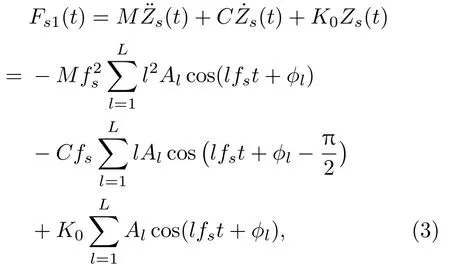
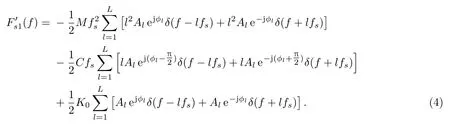
第二部分记为Fs2(t),其表达式见式(5),表示轮轨间弹性压缩量和Hertz弹簧动刚度相乘产生的弹性激励力作用的结果。Fs2(t)的傅里叶变换为F′s2(f),表达式见式(6)。Fs2(t)产生的响应信号频率主要为车轮多边形磨耗的激励频率,如图6(b)所示。

第三部分记为Fs3(t),其表达式见式(7),表示钢轨弯曲变形量和Hertz弹簧动刚度相乘产生的弹性激励力作用的结果。Fs3(t)的傅里叶变换为F′s3(f),表达式见式(8)。Fs3(t)产生的响应信号频率为车轮多边形磨耗激励频率两侧间隔分别为过轨频率fs及其倍频的调制边频带,如图6(c)所示。

将这3 部分进行叠加,得到图6(d)。从图6(d)中可以看出,系统存在过轨枕频率、多边形磨耗激励频率以及多边形磨耗激励频率两侧的调制边频带,这些频率和测试结果相吻合。因此,可以认为轮轨噪声存在边频带主要是过轨枕激励和多边形磨耗激励下的Hertz弹簧动刚度耦合作用导致的。另外,由于系统的等效阻尼以及相位差等参量未知,且难以计算,这些参量主要对幅值有影响,而不会对频率产生影响,故图6中的各图仅讨论各个频率之间的关系,在此进行统一说明。

图6 轮轨力频率特性Fig.6 Frequency characteristics of wheel-rail force
2.2 轮轨噪声仿真计算模型
通过上文分析可知,轮轨噪声存在边频带主要是过轨枕激励和多边形磨耗激励下的Hertz 弹簧动刚度耦合作用导致的,但是传统的基于TWINS 理论的轮轨噪声预测模型无法考虑此关系,需要对模型进行改进和优化。按照传统的基于TWINS 理论的轮轨噪声预测模型计算流程,需要先分别计算单位轮轨力激励下车轮、钢轨和轨道板的振动响应,进而求得单位轮轨力激励下车轮、钢轨和轨道板的辐射噪声。然后将车轮和钢轨粗糙度进行叠加,并通过滤波传递函数对粗糙度波长小于接触斑长轴的部分进行处理,求得联合粗糙度谱。接着可以通过公式(9)计算得到因轮轨不平顺激扰而产生的轮轨力。最后,将轮轨联合粗糙度谱激励下轮轨力频谱的平方与单位轮轨力作用下的声功率频谱相乘可得到实际声功率频谱[9]。事实上,运用TWINS轮轨噪声理论计算轮轨力时,主要采用移动粗糙度谱来对系统进行激扰,而车轮在轨道上的相对位置是不变的。显然,这无法表征在实际运行时,车轮和钢轨每时每刻不断变化的相对位移,不能考虑运行时轮轨之间的相互耦合作用,这一点从公式(9)中也可以看出。所以,采用此理论进行轮轨噪声预测时,一般无法考虑过轨枕冲击引起的噪声,而通过上文分析可知,轮轨噪声出现调制边频带和过轨枕冲击密切相关。因此,传统的TWINS轮轨噪声理论不再适用,需要对模型进行改进和优化。

式(9)中,r为联合粗糙度谱,αW为车轮轮轨接触点垂向位移导纳,αT为钢轨轮轨接触点垂向位移导纳,αC为轮轨垂向接触弹簧导纳(在TWINS 模型中,将Hertz弹簧视为线性)。
为更加准确地表征实际运行时的轮轨相互耦合作用,本文对传统的TWINS 轮轨噪声预测模型进行改进,建立时域下的车辆-轨道耦合动力学模型来代替原模型中对于轮轨力的求解方法。时域下的车辆-轨道耦合动力学模型虽然计算效率较低,但是能真实准确地表征车辆在运行过程中,轮轨间每时每刻的耦合作用,满足本文的研究需要。
本文轮轨噪声的计算流程如图7所示。首先,通过建立的车辆-轨道耦合动力学模型,计算当车轮表面存在非圆化磨耗时轮轨力随时间变化的曲线,接着对时域下的轮轨力曲线进行FFT变换,得到频率下的轮轨力。将此频域轮轨力输入TWINS 轮轨噪声计算模型,按照上文所述流程计算轮轨辐射噪声。故总体来说,本文的计算模型可以分为车轮-轨道耦合动力学模型和轮轨辐射噪声计算模型这两部分。

图7 轮轨噪声计算流程Fig.7 Wheel-rail noise calculation process
在车辆-轨道耦合动力学模型部分,将高速列车车辆系统简化为由一个车体、两个构架和4 个轮对组成的35 自由度的多刚体动力学系统,其中每个刚体考虑垂向、横向、点头、摇头和侧滚这个5 个方向上的自由度。连接车体、构架和轮对之间的一系、二系悬挂系统用弹簧阻尼系统模拟。对于轨道系统,采用整体混凝土道床轨道,由钢轨、扣件系统、轨道板及路基组成。其中左右钢轨被视为连续弹性离散点支承基础上的Timoshenko 梁,轨道板用三维实体有限元单元模拟,扣件系统用三维黏弹性弹簧-阻尼单元拟,路基支撑层简化为均匀分布的弹簧-阻尼单元连接。
采用迹线法来寻找轮轨接触点,在确定接触点之后通过插值计算得到接触点位置处的轮轨接触角。进一步的,利用Hertz接触理论可以计算得到轮轨法向力。利用Kalker线性理论和沈氏修正理论计算蠕滑率及力矩。
在整个计算过程中,涉及到大量的车辆-轨道系统动力学微分方程,采用显示积分方法对其进行求解(翟方法[11])。最终可以得到每一时刻下各个部件的位移、速度和加速度以及轮轨相互作用力。
此部分涉及内容较多,具体流程可以参考文献[11],故不在此赘述。
在轮轨辐射噪声计算模型部分,需要分别获取单位激励下的车轮、钢轨和轨道板的声辐射特性,再以通过车辆-轨道耦合动力学模型计算得到的轮轨力为输出,两者相乘得到实际轮轨力激励下的车轮、钢轨和轨道板的辐射噪声,最终将这三者求和得到轮轨辐射噪声。因此,对于此部分,关键是计算单位力激励下的上述子系统的辐射噪声特性。本文采用三维边界元方法对其进行求解,具体计算流程可以参考文献[12],故不在此赘述。
2.3 机理验证
通过实验研究,初步推测导致非圆化磨耗激励频率两侧出现轮轨噪声边频带的原因或许和过轨枕冲击有关。基于2.1 节中建立的轮轨噪声预测模型,分别计算以下3种工况下轮轨噪声的频谱特性。
工况1 存在非圆化磨耗的车轮运行于离散支撑轨道;
工况2 无非圆化磨耗的车轮运行于离散支撑轨道;
工况3 移动非圆化磨耗不平顺谱对轮轨系统进行激励,车轮和钢轨不发生相对运动,即不存在过轨枕冲击。
其中,车轮非圆化磨耗阶次为18 阶,列车运行速度为300 km/h,车轮直径为0.83 m,轨枕间距为0.625 m。
图8给出了上述3 种工况下计算得到轮轨噪声的频谱特性。图中,黑色实线、红色虚线和蓝色实线分别为工况1~3 条件下,轮轨噪声的频谱特性计算结果。

图8 轮轨噪声频谱特性计算结果Fig.8 Simulation results of wheel-rail noise spectrum
由工况1 条件下的轮轨噪声频谱特性可知,其噪声峰值频率为133 Hz(过轨枕频率)、578 Hz(非圆化磨耗激励频率)和445 Hz、710 Hz、842 Hz(调制边频带)当存在车轮非圆化磨耗的车轮运行于离散支撑的轨道上时,由于过轨枕激励和非圆化磨耗激励耦合作用,使得轮轨噪声产生了调制边频带。而由工况2 计算结果可知,轮轨噪声峰值频率为133 Hz(过轨枕频率),而无非圆化磨耗激励频率,也不存在调制边频带。由工况3 计算结果可知,轮轨噪声峰值频率为578 Hz(非圆化磨耗激励频率),而无过轨枕频率,也不存在调制边频带。因此,轮轨噪声边频带的产生是车轮非圆化磨耗激励和过轨枕激励耦合作用导致的,二者缺一不可。
3 轮轨噪声边频带影响因素研究
本小节基于上文所建立的轮轨噪声预测模型,在研究轮轨噪声边频带的影响因素的前提下,重点从列车运行速度、非圆化磨耗幅值、扣件刚度等方面开展研究。
3.1 列车运行速度
为研究列车运行速度对轮轨噪声调制边频带的影响,分别计算列车以160 km/h、200 km/h、240 km/h、300 km/h 和360 km/h 速度匀速运行时的轮轨噪声频谱特性,车轮直径为0.83 m,存在18阶非圆化磨耗,轨枕间距为0.625 m,计算结果如图9所示。
由图9可知,当列车以160 km/h 速度运行时,过轨枕频率为72 Hz,非圆化磨耗激励频率为309 Hz,无频率调制现象产生;当列车速度增加到200 km/h 时,过轨枕频率为89 Hz,非圆化磨耗激励频率为386 Hz,仍然无频率调制现象产生;当列车速度继续增大至240 km/h 时,过轨枕频率和非圆化磨耗激励频率也随之增大,并产生了轻微的频率调制现象;当速度继续增大至300 km/h 和360 km/h 时,在非圆化磨耗激励频率两侧出现明显的频率调制现象,且在300 km/h 时,频率间隔为133 Hz;在360 km/h 时,频率间隔为160 Hz,这和相应速度下的过轨枕频率相一致。总体来说当列车运行速度高于240 km/h 时,轮轨噪声频率调制现象才会发生。其原因在于,速度较小时,轮轨振动能量较低,难以激发其他频段的振动,随着运行速度地提高,振动能量也随之增大,进而导致轮轨噪声频谱中出现了调制边频带。

图9 运行速度的影响Fig.9 Spectrum of the wheel-rail noise at different speed levels
3.2 非圆化磨耗幅值
为研究车轮非圆化磨耗幅值对轮轨噪声调制边频带的影响,分别计算当列车存在非圆化磨耗幅值为0.001 mm、0.002 mm、0.003 mm、0.005 mm、0.008 mm、0.01 mm、0.02 mm 和0.03 mm 时的轮轨噪声频谱特性,车轮直径为0.83 m,非圆化磨耗阶次为18阶,列车运行速度为300 km/h,轨枕间距为0.625 m,计算结果如图10所示。其中,图10(a)为0~1000 Hz频段内的轮轨噪声频谱特性,由于图中曲线较多,为了便于比较规律,图10(b)~(e)分别给出了578 Hz(非圆化磨耗激励频率)、133 Hz(过轨枕频率)、455 Hz(边频)和710 Hz(边频)处的轮轨噪声峰值。
由图10 可知,随着车轮非圆化磨耗幅值的增加,在非圆化磨耗激励频率处的轮轨噪声峰值也明显增大,而过轨枕频率处的峰值则基本不变。对于非圆化磨耗激励频率峰值两侧的边频峰值,当非圆化磨耗幅值为0.001 mm 时,基本上不存在边频峰值,随着非圆化磨耗幅值的增加,其边频峰值也随之增大。可以认为当非圆化磨耗幅值超过0.005 mm 时,轮轨噪声会产生明显的频率调制现象。

图10 非圆化磨耗幅值的影响Fig.10 Influence of the amplitude of polygonal wear
3.3 扣件刚度
为研究扣件刚度对轮轨噪声调制边频带的影响,分别计算当扣件刚度为20~100 kN/m 时的轮轨噪声频谱特性,车轮直径为0.83 m,非圆化磨耗阶次为20 阶,幅值为0.01 mm,列车运行速度为300 km/h,轨枕间距为0.625 m,计算结果如图11所示。其中,图11(a)为0~1000 Hz 频段内的轮轨噪声频谱特性,由于图中曲线较多,为了便于比较规律,图11(b)~(e)分别给出了578 Hz(非圆化磨耗激励频率)、133 Hz(过轨枕频率)、455 Hz(边频)和710 Hz(边频)处的轮轨噪声峰值。
由图11 可知,随着扣件刚度的增大,非圆化磨耗激励频率处的轮轨噪声峰值减小,而过轨枕频率处的轮轨噪声峰值增大。对于非圆化磨耗激励频率峰值两侧的边频峰值,随着扣件刚度地增大也呈增大的趋势。

图11 扣件刚度的影响Fig.11 Influence of the rail pad stiffness
4 结论
本文通过实验分析、理论推导和数值仿真,对车轮非圆化磨耗激励下轮轨噪声频谱上产生调制边频带这一现象展开研究。主要得到以下结论:(1)当带有非圆化磨耗的车轮运行时,轮轨噪声窄带频谱上出现了以非圆化磨耗激励频率为中心,以过轨枕频率为间隔,等间距分布的噪声峰值(即存在边频带);(2)轮轨噪声存在边频带主要是过轨枕激励和非圆化磨耗激励下耦合作用导致的;(3)列车运行速度、非圆化磨耗幅值和扣件刚度等因素均对轮轨噪声边频带有影响;(4)通过仿真分析并结合实际情况可知,严格控制车轮多边形磨耗水平是抑制轮轨噪声边频带产生的最有效方法。
