基于遗传算法的传声器阵列位置有源校正研究∗
2022-03-05邵祚桪郑成诗李晓东
邵祚桪 厉 剑 郑成诗 李晓东
(1 中国科学院声学研究所 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
传声器阵列具有丰富的空时信息,能够降低噪声,抗干扰,进行灵活波束控制,实现声源定位、识别、增强与分离等功能。传声器阵列按照几何结构,可以分为一维线性阵列、二维平面阵列以及三维阵列,其中二维平面阵列广泛应用于设备故障检测、鸣笛检测、远距离拾声等应用场景[1−2]。在应用过程中,传声器阵列的机械加工与安装会导致位置不精确,产生平移与旋转误差等问题,使得传声器阵列相关算法在高精度定位应用场景达不到预期效果,因此需要研究阵列位置校正方法,从而提高定位性能。
针对传声器阵列位置校正问题,相关学者提出了一系列解决方法。文献[3–5]使用已知位置的校正信号源,利用特定形状传声器阵列的到达方向(Direction of arrival, DOA)信息,建立代价函数,通过迭代算法求解出各阵元的位置。文献[6]利用阵列的到达时间(Time of arrival, TOA)建立模型,对阵列形状和幅度进行校正。文献[7–9]对到达时间模型的代价函数进行改进,并采用不同的改进优化算法,提高了位置校正的准确性,并提高了收敛速度。上述基于TOA 方法需要将声源与测量设备进行时钟同步,实际应用中对于设备性能要求较高。文献[10]通过建立最大似然方程,实现了阵元位置与声源DOA信息的联合估计。文献[11]利用特征值分解法建立矩阵方程,利用最小二乘法,实现了阵元位置和幅相误差的联合估计,在高信噪比(Signal-noise ratio, SNR)下有较好的性能。文献[12]利用多元变量分析对阵元几何结构进行校正,并分析了算法对于阵列孔径与位置的敏感度,验证了较大的阵列尺寸可以保证校正准确性。在室内场景应用场景中,文献[13]考虑晚期混响的影响,在多元变量分析的基础上,引入多通道线性预测(Multi-channel linear prediction, MCLP)方法,提高了阵列位置估计的准确性。但是,上述方法在信号模型时均假设各阵元位置误差彼此独立,不能直接应用于形状固定的阵列位置校正问题。
本文针对形状固定的阵列位置校正问题,提出了一种基于遗传算法的位置参数有源校正方法。首先,在校正声源坐标已知的情况下,利用广义互相关函数法(Generalized cross-correlation, GCC)估计每对传声器的到达时间差(Time difference of arrival, TDOA)并利用线性插值方法进行修正,构造均方误差代价函数,再通过遗传迭代算法最小化代价函数,得到全局最优解。仿真及实验结果表明,本方法校正误差更小,且鲁棒性较强,在阵列的各种应用场景具有普适性和实用性。
本文的主要内容如下:第1 节介绍了阵列与信号的模型;第2 节介绍了校正算法的具体原理与详细步骤;第3 节给出阵列校正算法的仿真及结果分析;第4 节介绍了实验及结果分析;第5 节为本文结论。
1 阵列模型介绍
考虑三维空间中一个由K个阵元组成的二维平面阵列,当存在J个时域或频域可分的校正声源时,第j个声源向该阵列的第k个阵元入射,则该阵元接收到的信号频域模型可表示为

其中,j=1,2,···,J,k=1,2,···,K,Sj(ω)表示第j个声源的输入信号,Hkj(ω)表示空间内第j个声源到第k个阵元的传递函数,Wkj(ω)表示加性噪声。
本文以阵列相对坐标对阵列传声器分布进行描述,以阵列所在平面为相对坐标yOz平面,以yOz平面内某点为坐标原点并由原点定义坐标轴,如图1所示。设该阵列的相对坐标下第k个阵元的坐标为rin,k= [xin,k,yin,k,zin,k],其中k= 1,2,···,K。以Tait-Byrne 角[14]的标准形式对该阵列进行旋转变换,先后绕着相对坐标中的z轴、y轴、x轴旋转角度α、β和γ,再将此阵列按照相对坐标中心在全局坐标中的位置平移rm= [x0,y0,z0],则坐标变换后各阵元的全局坐标为

图1 阵列的相对坐标模型Fig.1 The relative coordinate model of array
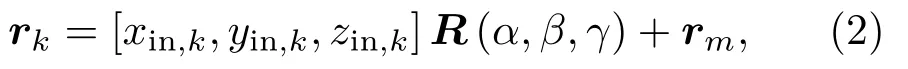
其中,
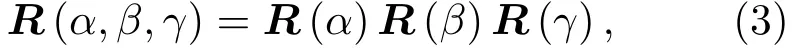
表示阵列分别绕z轴、y轴、x轴旋转角度α、β和γ方式下的旋转矩阵,其中,

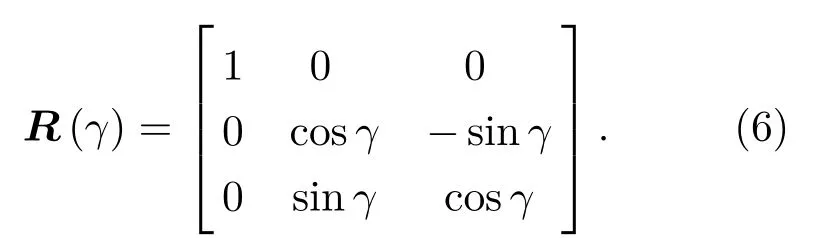
因此描述该阵列在三维空间内平移与旋转的待求未知参数集u可表示为
2 基于遗传算法的阵列校正
使用迭代算法可对阵列参数集u各变量进行估计,本文提出采用遗传算法[15]进行迭代求解,下面对校正算法的步骤进行阐述。
2.1 代价函数
遗传算法需要设定代价函数表示适应度,针对本文的阵列校正问题,代价函数设为该阵列的每对阵元TDOA均方误差函数。
本文阵列模型考虑阵列与校正源的三维坐标,因此将校正声源视作球面波。由于阵列中各阵元位置不同,声源到各阵元存在到达时间差。当第j个声源信号入射时,对应的第l个阵元与第k个阵元(k≠l)接收信号分别为Xlj(ω)与Xkj(ω),可利用GCC 函数估计两路信号的到达时间差[16]。两路信号的广义互相关函数为
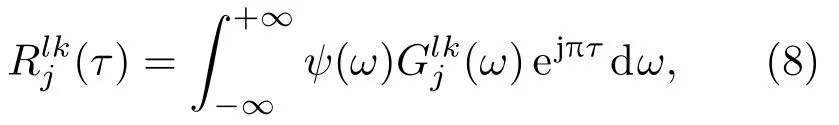
其中,ψ(ω)为GCC 的加权函数,Glkj(ω)为通道l和通道k信号的互功率谱。对广义互相关函数进行峰值检测可得到TDOA的估计值。由于使用GCC估计TDOA的精度受制于传声器的采样率,为提高TDOA 估计的精度,可对互相关函数进行线性插值再进行峰值检测。通过各阵元到声源距离的几何关系,可得到TDOA的理论值为

其中,rl和rk表示阵元l和阵元k的全局坐标,rj= [xj,yj,zj]表示第j个声源的全局坐标,c为声速。
将该阵列内每对阵元TDOA 的均方误差相加,由此可得关于声源j的均方误差表达式:
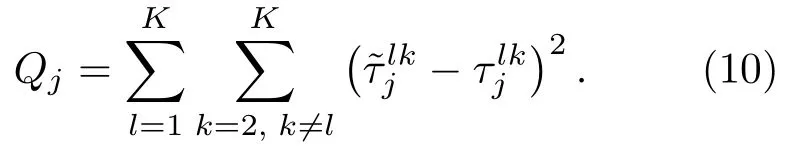
再将所有J个声源均方误差相加,得到总体代价函数:

迭代过程中,代价函数越小,表明该个体适应度越高,该函数为遗传算法筛选种群的唯一准则,代价函数对应的全局最优解为

依据以上步骤,可得到迭代算法使用的代价函数,从而估计出各位置变量。
2.2 校正步骤
遗传算法模拟生物学中的遗传规律,对一个种群中的个体进行选择、交叉、变异等过程进行概率化寻优,求解全局最优解。基于遗传算法的阵列位置校正大致步骤如图2所示,具体包括:
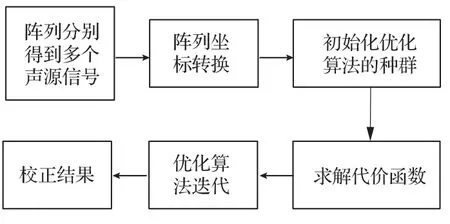
图2 本文提出的阵列校正算法步骤Fig.2 The procedure of the proposed array calibration algorithm
(1)精确测量多个校正声源的位置,使用阵列采集声源信号,要求声源时域或频域可分。
(2)利用初步预计的阵列参数进行阵列坐标转换,对阵列的TDOA 进行估计,作为遗传算法的输入变量。
(3)初步测量阵列各位置参数[x0,y0,z0,α, β,γ],设置其中各变量的上下限,创建个体数为N的遗传算法最初种群U=[u1,u2,···,uN],种群中每个个体u1,u2,···,uN各位置参数由高斯分布产生,参数均值为初步测量所得数值,若超出预定上下限则重新生成,将每个个体的所有位置参数作为遗传算法中的基因。设置遗传算法的遗传代数(及即迭代次数)。
(4)对种群每个个体进行适应度(即代价函数Q)的计算。记录种群最佳适应度、平均适应度与最佳的染色体。
(5)使用轮盘赌准则,对父代选出合适的染色体传入下一代。
(6)使用单点交叉法,在基因中随机寻找某个交叉点,使得某一对个体的基因进行彼此交换。
(7)对于个体的基因进行随机的基本位变异。
(8)依据适应度选出上一次最佳与最劣适应度的染色体及其在种群的位置,新一次迭代最佳的染色体替代上一次最劣的位置,并记录此时的平均适应度与最佳适应度。
(9)若达到最大遗传代数,则停止迭代并输出最佳染色体;若未达到则产生新的种群,编码并进入步骤(4)继续迭代,直至迭代结束。遗传算法输出结果即为阵列位置参数的全局最优解。
3 仿真结果与分析
3.1 阵列位置校正方法比较
本文将上述方法与文献[3]、文献[17]中的方法进行比较,本文方法与其他文章方法均采用迭代算法求解目标变量,本文主要比较各方法代价函数的性能,优化算法均使用2.2节所述的遗传算法步骤。
文献[3]为DOA-Based 方法,对特定形状阵列接收到校正源j的信号,使用广义互相关函数估计部分传声器对之间的TDOA,从而计算出相对坐标下的方位角与俯仰角,再利用阵列各阵元与声源距离的几何关系,计算出方位角与俯仰角θj与φj的理论值,其中j=1,2,···,J。每个声源对应的角度均方误差求和可得到代价函数:
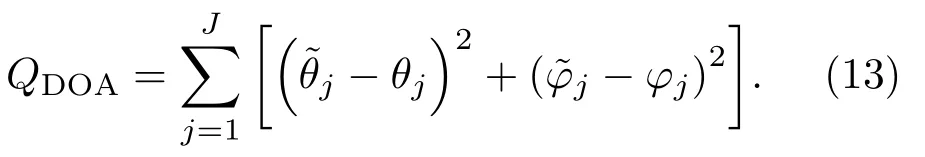
文献[17]为特征空间ES-Based(Eigenstructure-Based)方法,该方法利用多信号分类(Multiple signal classification, MUSIC)算法得到代价函数。设Rs,j(ω)为阵列各通道接收到校正源j的信号在频率ω下的协方差矩阵,将协方差矩阵进行特征值分解,得到特征向量矩阵Uj= [uj,1,uj,2,···,uj,K],其中uj,1为信号子空间的特征向量,uj,2,uj,3,···,uj,K为噪声子空间的特征向量。由此得到噪声子空间矩阵Un,j(ω)= [uj,2,uj,3,···, uj,K]。通过估计出的噪声子空间矩阵ˆUn,j(ω)得到MUSIC 空间谱在声源j对应的代价函数,将所有声源对应的值相加得到总代价函数:
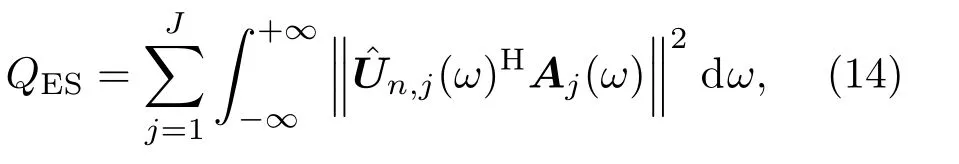
其中,Aj(ω)表示在频率ω下阵列各阵元到声源j的导向矢量,符号“(·)H”表示矩阵的共轭转置,符号“‖·‖”表示矩阵的F-范数。
为比较本文方法与上述文献方法的性能,本文选取二维平面传声器阵列的应用场景之一的鸣笛声定位场景[18]进行校正仿真,使用4×8 的平面均匀矩形阵列,阵元共32个,相邻阵元相距0.04 m,将该阵列角上的阵元位置定义为该阵列的相对坐标原点。
校正源使用信号为时长2 s 的鸣笛信号,对应语谱图如图3所示。本文仿真中在各传声器加入互不相关的白噪声,测试不同信噪比下的各种算法的校正性能。本文考虑全频带定位方法下的阵列校正问题,在仿真测试中公式(8)中ψ(ω)在所有频率上均取1。

图3 鸣笛的语谱图Fig.3 The spectrogram of the whistle
鸣笛的户外场景应用以环境噪声为主而混响较低,本文在仿真中只考虑直达声模型,即公式(1)中的传递函数Hkj(ω)取1。面阵原始位置(即上述阵元的相对坐标原点的位置)[x0,y0,z0,α,β,γ]参数分别为(1 m, 1 m, 8 m, 0°, 0°, 0°),坐标参数搜索范围为原位置±0.1 m,角度参数搜索范围为原位置±5°。声源坐标分别为(10 m, 5 m, 1 m)、(10 m,0 m, 1 m)、(20 m, 5 m, 1 m),阵列与校正源位置的示意图如图4所示。按照全局信噪比30 dB、20 dB、10 dB 三种情况仿真,每种信噪比情况进行20 次Monte-Carlo测试,其余仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters
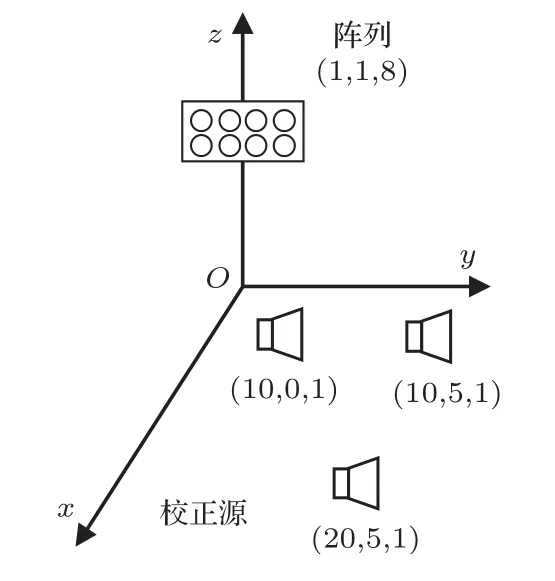
图4 仿真场景示意图(单位:m)Fig.4 The schematic diagram of the simulation scene(unit: m)
图5给出了本文方法(Proposed)、DOA-Based方法、ES-Based 方法对于阵列坐标参数与阵列旋转角度参数的平均校正误差。图5(a)~(c)结果表明,在信噪比10 dB 及以上的多数情况下,对坐标参数的估计,本文方法误差小于DOA-Based算法与ES-Based 算法,最大误差限制在0.016 m 以内。图5(d)~(f)结果表明,在各信噪比下,本文方法对角度参数的估计误差也总体小于其他两种算法,最大误差限制在0.08°以内。
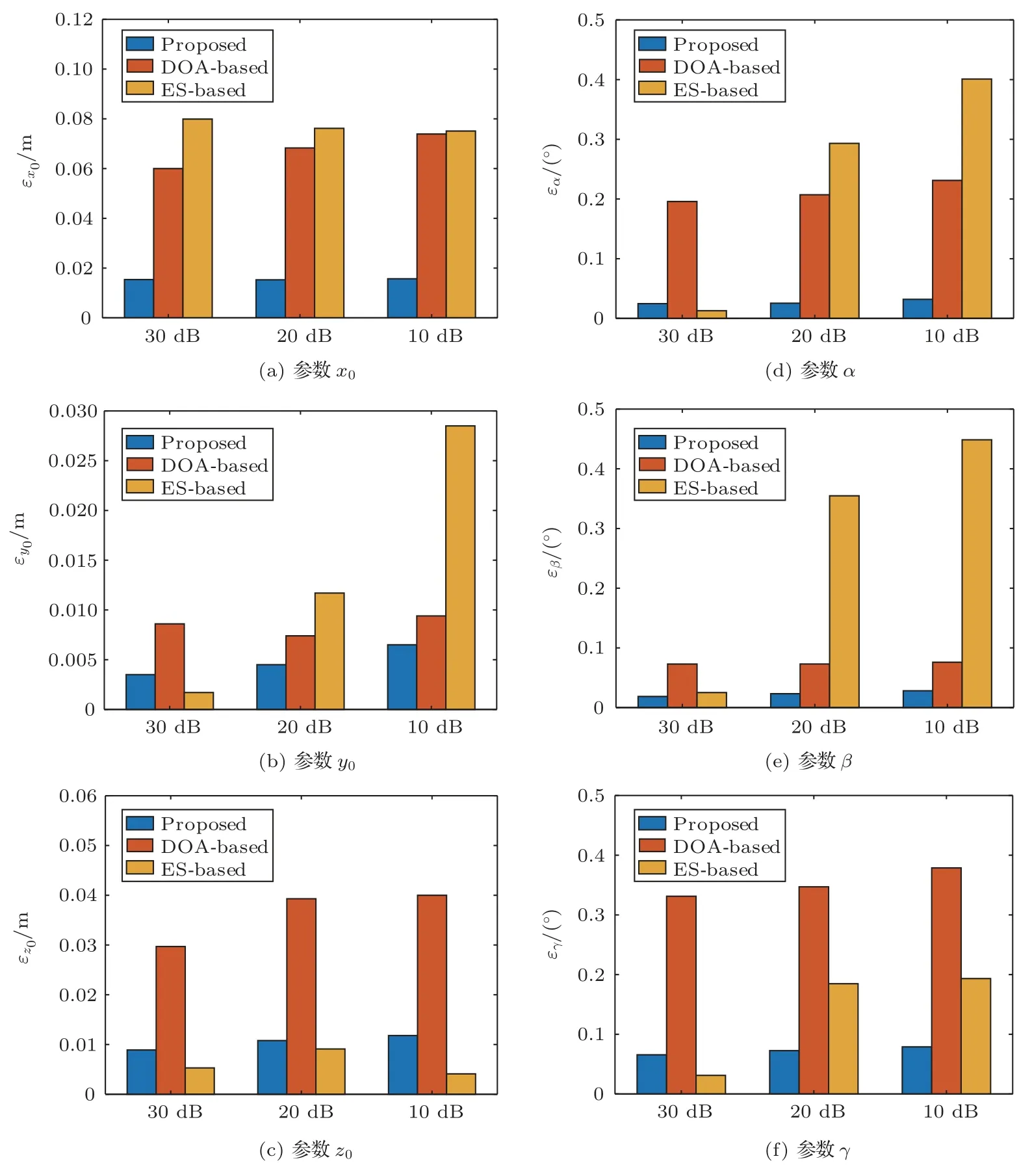
图5 不同信噪比下各方法阵列参数校正平均误差Fig.5 The average calibration errors of array parameters with different SNRs
经分析,DOA-Based 算法使用远场模型,仅考虑角度变量,未考虑各阵元至声源的距离变量,影响了代价函数的准确性。ES-Based 方法中MUSIC 算法空间谱在特定方向上可形成极高的谱峰,但该方法对噪声较敏感,噪声环境下声源方向空间谱的实际值与理论值存在偏差,影响迭代中全局最优解的搜索。本文方法采用近场模型,考虑阵列与声源的三维坐标,同时在GCC 函数中引入线性插值,提高了低信噪比下TDOA估计的准确性,使得迭代过程中阵列各位置参数更容易收敛至预期位置。
综上所述,相比于传统的DOA-Based 和ESBased 方法,本文提出的方法可以获得更加准确的阵列位置参数的估计性能。
3.2 阵列存在不一致时的校正性能
传声器阵列在制造或使用的过程中会产传声器之间幅度响应或相位响应不一致的情况,为验证传声器不一致情况下本文算法的鲁棒性,本文进行如下对比仿真,其中阵元不一致的情况包括:
(1)假设各个传声器阵元的幅度存在−1~1 dB均匀分布的误差;
(2)假设各个传声器阵元的相位存在−3° ~3°均匀分布的误差;
(3)假设各个传声器阵元的相位存在−3° ~3°均匀分布的误差,且幅度存在−1~1 dB 均匀分布的误差。
仿真中其他参数条件、遗传算法参数均与3.1节所述相同。表2~4 分别给出了情况(1)、(2)、(3)对应的位置参数校正平均误差,其中误差最小的数据进行了加粗处理便于显示。由仿真结果可知,与其他两种算法相比,本文提出的校正算法在绝大多数情况下的参数误差均为最小,因此本文算法在传声器阵列幅度与相位不一致的情况下具有更好的鲁棒性。

表2 传声器阵列幅度不一致时参数校正平均误差Table 2 The average calibration errors of array parameters when the amplitudes of different microphones are inconsistent
3.3 声源位置对校正性能的影响
在实际应用中,声源位置的选取会影响到传声器阵列位置校正的准确性,为研究声源位置本文所提出校正方法性能的影响,本节采取不同的声源位置组合分别进行仿真。
本节仿真假设仿真场景模型为直达声模型。阵列原始位置(1 m, 1 m, 8 m, 0°, 0°, 0°),坐标参数搜索范围为原位置±0.1 m,角度参数搜索范围为原位置±5°,仿真参数与表1相同。仿真在50 m×20 m的矩形区域进行3 个声源的放置,这里将x轴方向定义为主要的距离方向,x轴数值越大代表距离阵列越远,位置组合包括:
(A)近距离集中布放:(1 m, 1 m, 1 m),(1 m,2 m, 1 m),(2 m, 1 m, 1 m);
(B)远距离分散布放:(50 m,10 m,1 m),(50 m,15 m, 1 m),(50 m, 20 m, 1 m);
(C)远距离集中布放:(50 m, 1 m, 1 m),(50 m,2 m, 1 m),(50 m, 3 m, 1 m);
(D)中距离分散布放:(20 m,10 m,1 m),(25 m,10 m, 1 m),(30 m, 10 m, 1 m);
(E)不同距离分散布放:(1 m,1 m,1 m),(20 m,10 m, 1 m),(50 m, 20 m, 1 m)。
表5给出了不同声源位置组合下各参数的平均校正误差,在6 个位置参数在3 种信噪比条件下共有18 种情况。由仿真结果可知,校正声源位置的选择会影响各个参数的估计误差结果。对比5 种布放组合的18个校正结果可知,组合(E)在11个变量上平均误差小于其他组合,且多数情况为旋转角度校正误差较小。这是因为声源位置分布较为分散的情况下,阵列微弱的角度偏转对TDOA 的影响较大,使得以TDOA 均方误差作为代价函数的校正算法对旋转角度的估计更准确。此外,当声源布放在x轴方向较远情况时(即组合(B)和组合(C)),平移坐标的估计误差总体大于其他情况,这是因为声源距离阵列较远的情况下,阵列TDOA值的变化量对阵列的平移不敏感,导致错误阵列位置对应的代价函数与正确位置相差较小,因此迭代算法容易收敛错误。
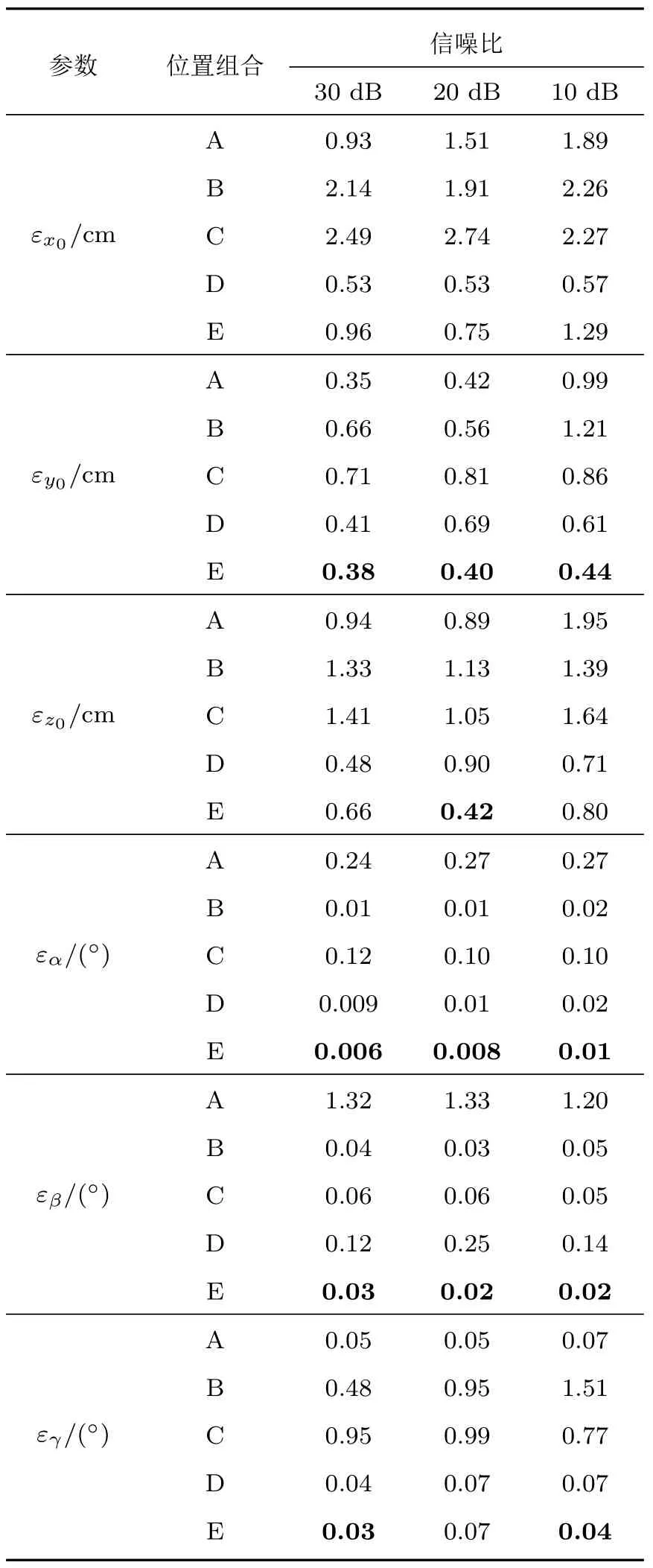
表5 不同声源位置组合下的参数校正平均误差Table 5 The average calibration errors of array parameters when using different combinations of sound sources with different positions
基于上述仿真结果,在声源个数有限的情况下使用本文方法进行阵列校正时,应采用声源位置较为分散布放方式提高参数校正精度。
3.4 其他形状阵列校正
为验证本文方法适用于不同形状阵列的位置校正,本文另选取3 种形状的阵列进行校正算法仿真,阵列形状包括:
(a)十字阵列,阵元共32个,每一分支上相邻阵元间距0.04 m;
(b)螺旋阵列,阵元共32个,螺旋每层半径相距0.04 m;
(c)随机阵列,阵元在坐标范围x ∈[−0.2,0.2]、y ∈[−0.2,0.2]内均匀分布产生,阵元共32个。
图6给出了3 种阵列在相对坐标下各阵元的位置。

图6 不同阵型示意图Fig.6 The schematic diagrams of arrays with different formations
仿真条件与3.1 节相同,假设仿真场景模型为直达声模型。阵列原始位置(1 m, 1 m, 8 m, 0°, 0°,0°),坐标参数搜索范围为原位置±0.1 m,角度参数搜索范围为原位置±5°。声源位置(10 m, 5 m,1 m),(10 m, 0 m, 1 m),(20 m, 5 m, 1 m)。信噪比按照30 dB、20 dB、10 dB 三种情况仿真,每种信噪比情况进行20 次Monte-Carlo 测试,其余仿真参数如表6所示。
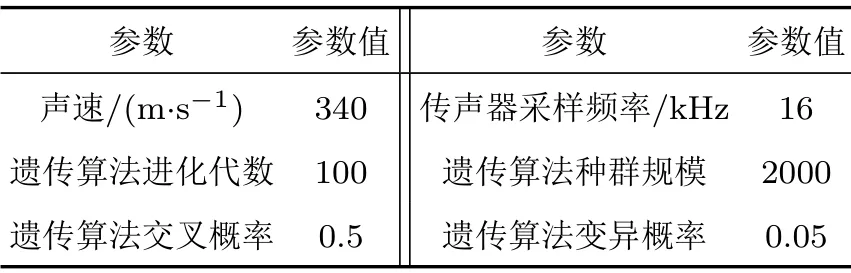
表6 仿真参数Table 6 Simulation parameters
表7给出了十字阵列(a)、螺旋阵列(b)、随机阵列(c)的平均校正误差。仿真结果表明,在10 dB及以上的信噪比情况下,本文方法在多数物理量估计的误差都小于DOA-Based方法与ES-Based方法,本文提出的方法适用于多种类似阵列,且阵列位置的估计性能优于其他两种方法。
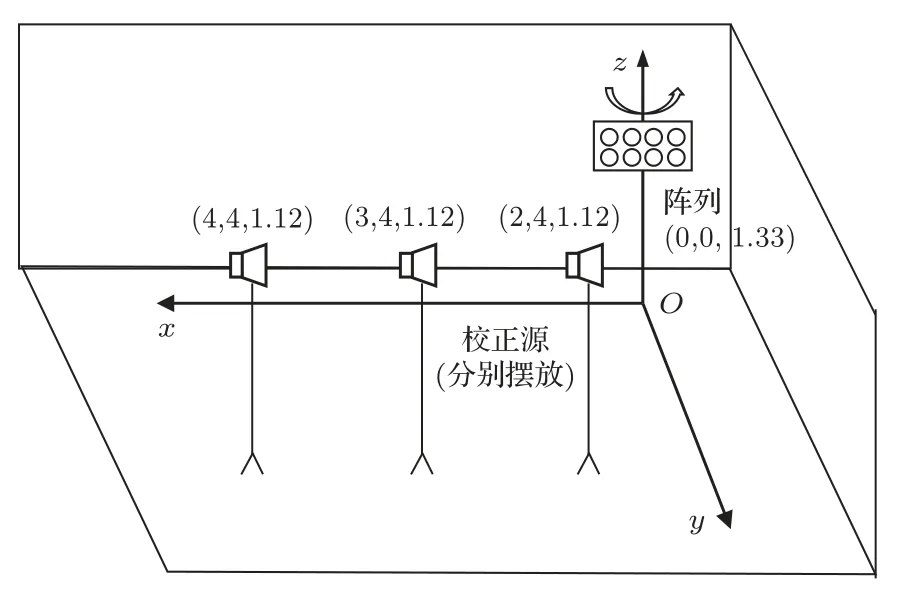
同时由表7可知,在使用本文方法情况下,坐标参数平均误差满足a 表7 不同信噪比下各形状阵列参数校正平均误差Table 7 The average calibration errors of array parameters for the arrays of different formations with different SNRs 本节利用矩形阵列分析上述各个阵列位置校正算法在半消声室中的性能。测试所使用的半消声室长宽高尺寸为14.8 m×8.8 m×7.2 m。实验使用的阵列为4×8的矩形均匀面阵,阵元间距为0.04 m,采样率为16 kHz。录声使用专用系统综合测试软件控制采集板。校正声源为惠威H4 扬声器播放的鸣笛声,信号源与图3所示相同。阵列中心位置(2 m,4 m, 1.33 m),校正源位置(2 m, 4 m, 1.12 m),(3 m,4 m, 1.12 m),(4 m, 4 m, 1.12 m),声源与采集板摆放位置的示意图如图7所示,场景实际拍摄图片如图8所示。 图7 实验场景示意图(单位:m)Fig.7 The schematic diagram of the experiment scene(unit: m) 图8 实验场景图片Fig.8 The photo of the experiment scene 实验步骤如下: (1)建立空间直角坐标系,确定坐标轴方向,设置3个声源,准确测量声源位置; (2)摆放阵列,使得采集板大致与y轴方向垂直,大致测量其位置,定义此时其绕着z轴的偏转角度为0°; (3)在预定声源位置先后分别播放2 s 鸣笛,使用采集板进行录声; (4)将阵列绕z轴分别旋转5°、10°、15°,重复步骤(3)。 利用4种阵列角度下阵列分别接收到的校正源信号,估计出每次的α角度,以第一轮实验位置为基准0°,后3 次阵列旋转情况下估计出的α与原始位置的α做差,得到Δα,每次角度重复估计5次,求出角度估计的均值与标准差。实验所使用参数如表8所示。 表8 实验参数Table 8 Experiment parameters 该实验对本文提出方法、文献[3]所述DOABased 方法及文献[17]所述ES-Based 方法的性能进行测试。图9的误差棒图给出了本次实验中3 种校正方法对Δα的估计结果,其中点线与符号“o”代表真实的旋转角度(True),实线代表本文方法下旋转角度估计的平均值与标准差,虚线代表DOABased方法估计结果,点划线代表ES-Based 方法估计结果。 图9 阵列旋转角度估计结果Fig.9 The estimated results of array rotations for different angles 由实验结果可知,在不同旋转情况下的角度估计中,本文方法估计误差总体低于其他方法,最大误差仅0.76°,具有较高的准确性。此外,本实验在不同α角度上多次重复估计下的标准差也明显小于其他两种方法,最大标准差仅为0.32°,这说明利用遗传算法进行校正,在相同参数与迭代次数的情况下,本文方法所使用代价函数更易收敛至全局最优解。综上,该实验的结果证明了本文方法具有更好的校正性能。 本文提出了一种对二维平面传声器阵列的坐标参数与旋转角度参数校正的方法。首先利用TDOA估计值与理论值构造均方误差代价函数,再使用遗传算法搜索全局最优解使得代价函数最小,由此求解阵列的位置参数。本文在不同信噪比情况下,对不同形状的阵列进行了位置参数估计的仿真,并进行半消声室的实测数据验证。仿真与实验结果表明,使用该代价函数并使用遗传算法进行优化可得到较为准确的位置参数,该方法在不同信噪比情况下校正误差总体小于DOA-Based 算法与ES-Based 算法,并且适用于不同形状的传声器阵列,收敛结果稳定,鲁棒性更强。
4 实验验证



5 结论
