基于准弹性修正法计算道岔区轮轨接触关系

2022-08-06罗燕陈嵘袁钰雯徐井芒钱瑶

铁道建筑 2022年7期

罗燕陈嵘袁钰雯徐井芒钱瑶

1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.西南交通大学土木工程学院，成都 610031

轮轨磨耗影响轮轨间的相互作用，进而影响列车运行时的平稳性和安全性［1］。相较于区间线路，道岔区结构复杂，列车过岔时，轮轨磨损更加严重［2］。

国内外专家对轮轨接触几何展开了大量研究。王开文［3］提出了迹线法求解任意车轮踏面和钢轨廓形的轮轨接触几何参数。倪平涛等［4］利用迹线法和钢轨廓形分区法求解钢轨不同区域与车轮的最小间隙差，以此判断单点或多点接触。曹洋［5］对岔区控制断面进行插值得出任意计算断面，结合迹线法计算不同断面的轮轨接触参数。Sugiyama 等［6］提出一种可用于道岔区轮轨两点接触几何分析的数值计算方法，并讨论了尖轨变截面廓形对道岔区轮轨接触几何的影响。钱瑶［7］提出求解道岔区轮轨接触接触几何的法向切割法，此法能准确求解在不同横移量和摇头角下岔区轮轨接触点的位置，并在此基础上分析了车轮磨耗对岔区轮轨接触几何的影响。上述方法均假设钢轨和车轮为刚体，为刚性接触法。此类方法计算速度快，但对于不光滑的车轮踏面和钢轨顶面，计算出的接触点会有较大的跳跃。

因此，Arnold［8］提出了一种准弹性接触法，对刚性接触法计算出的接触点进行修正和优化，求解一定轮重下的实际轮轨接触点，并将此方法用于动力学仿真软件SIMPACK 的轮轨接触关系计算中［9］，但在SIMPACK 的轮轨关系模块中未考虑轮对横移时的侧滚。干锋等［10］结合轮轨刚性接触法和准弹性接触模型研发了TPLWRSim 软件，用于计算磨耗后车轮踏面的轮轨接触关系。

上述研究大多针对区间钢轨，未针对道岔区钢轨的特殊结构。研究考虑弹性的道岔区轮轨接触算法可以为求解道岔区轮轨接触力学、轮轨动力学提供理论基础。因此，本文运用法向切割法结合准弹性接触模型计算磨耗前后地铁列车LM 型踏面和9 号道岔匹配的轮轨静态接触参数，对比分析准弹性修正前后轮轨接触点及轮轨接触几何参数的差异。

1 钢轨和车轮廓形

1.1 钢轨廓形

9 号道岔转辙器区基本轨侧钢轨廓形沿纵向不变。对于尖轨侧尖、基本轨组合廓形，首先通过CAD软件离散并提取控制断面廓形坐标，再利用控制断面进行线性插值得到中间任意计算断面。在进行插值时需将尖轨和基本轨分开离散和插值。图1为尖轨侧控制断面和插值得到的不同顶宽尖轨和基本轨的组合廓形。

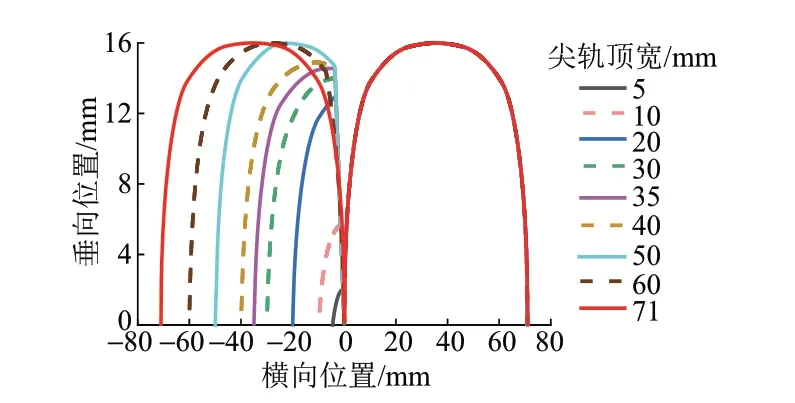
图1 道岔尖轨断面

1.2 车轮廓形

采用Miniprof 测量了上百组服役状态下的地铁车轮踏面，并对实测廓形数据进行处理，除去噪声点并进行拟合和平均化，得到磨耗车轮踏面，进行坐标变换后与标准LM 踏面对比，结果见图2。可知，磨耗车轮踏面和轮缘均有一定磨损，其中踏面主要发生垂向磨耗，最大磨耗量为1.32 mm，轮缘发生侧面磨耗。

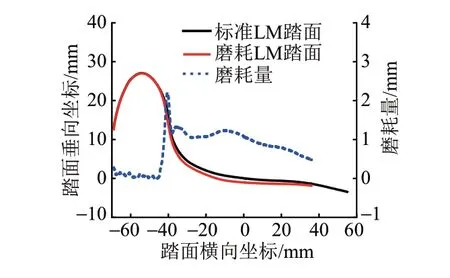
图2 磨耗车轮踏面与标准车轮踏面对比

2 法向切割法及准弹性修正法

2.1 法向切割法

法向切割法［7］是一种考虑道岔变截面特点的轮轨静态几何接触点算法。假设轮对和钢轨均为刚体，且左右轮轨同时接触，接触点处轮轨间垂向间隙最小。

计算时把车轮表面看作是由一条车轮廓形线绕车轴中心线旋转360°得到的曲面，车轮底部垂直于轮轨坐标系中x= 0 平面的轮廓线称为主轮廓线，其上任意一点坐标为[0，y0，z0]，车轮上其他任意轮廓线所在二维平面与主轮廓线所在平面间的夹角为α，称为法向切割角。该轮廓线上任意一点坐标可表示为

求解轮轨接触点时，给定初始的法向切割角为[αa，αb]，在此范围内把车轮曲面等分为n+1 条车轮廓形线。在轨道坐标系中任一轮廓线坐标为

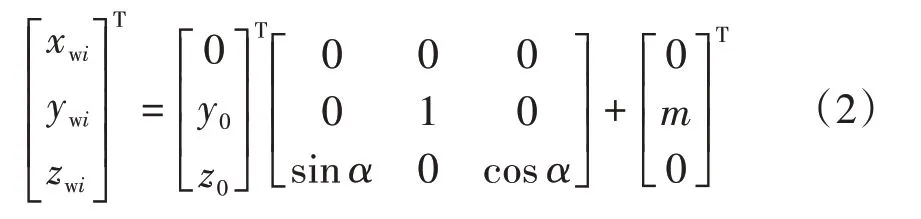
式中：m为轮对中心到名义滚动圆位置的距离。

已知轮对摇头角为δ，横移量为yw，假设轮对初始侧滚角为θ，则计算时任一车轮廓形线坐标为

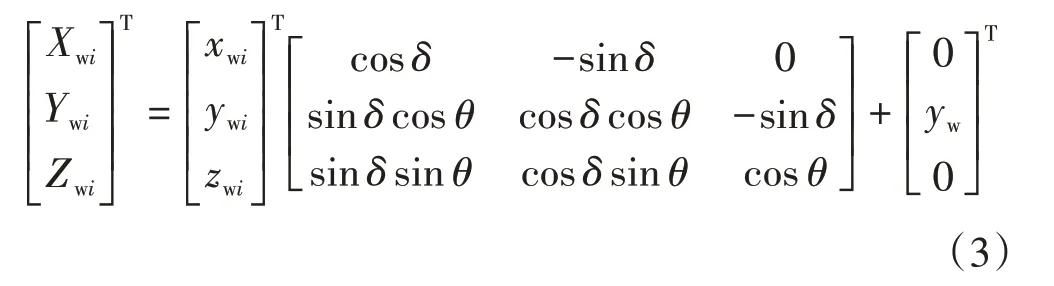
获得法向切割角范围内车轮廓形线离散点坐标后，插值得到尖轨侧尖轨和基本轨组合廓形在相同坐标系中的离散点。根据最小距离法求在初始侧滚角下左侧最小距离d0L，min和右侧最小距离d0R，min的差值d0，min=d0L，min-d0R，min及对应的车轮线法向切割角α0。在新的法向切割角范围[α0-(αa+αb)/(2n1)，α0+(αa+αb)/(2n1)]内，对车轮重新法向均分切割成n1份，再计算得新的最小距离差d1，min与对应的车轮线法向切割角α1。如果|d1，min-d0，min| ≤Δ（Δ 为计算需满足的精度），则最小距离点在法向切割角为α1的车轮线上，否则应继续在新的法向切割角范围内进行最小距离差的求解，直到第k次计算满足|dk，min-dk-1，min| ≤Δ，此时的法向切割角为αk，即在初始侧滚角θ下的最小距离差为f(θ) =dk，min。在该车轮线上考虑侧滚角的影响，根据经验给出侧滚角范围[θc，θd]，θm=（θc+θd）/2，若f(θm)= 0，则当侧滚角为θm时轮轨刚好接触，否则用二分法对f(θ)进行迭代，直到|θc-θd| ≤Δ，满足精度要求。由此求得在摇头角为δ、横移量为yw时轮轨接触的侧滚角及接触点坐标。

2.2 准弹性修正法

在对轮轨接触参数进行计算时，刚性接触法计算速度快，但计算结果不够准确。弹性接触法考虑轮轨实际材料特性，计算精度高，但计算过程繁琐，计算效率低。准弹性接触法［11］计算速度快，同时计算结果准确性较高。

车轮与轨道静态接触时，接触条件与基本特征为：左右轮与钢轨同时接触，且接触位置轮轨垂向距离最小；轮对横移时会产生侧滚运动；在名义滚动圆附近的轮轨常接触区域，轮轨接触点位置不会产生大的跳变。

假设车轮与钢轨轮廓线上垂向两点间对应的位置矢量为q，横向坐标为s，两点间的垂向距离为d(s，q)，轮轨接触几何条件为

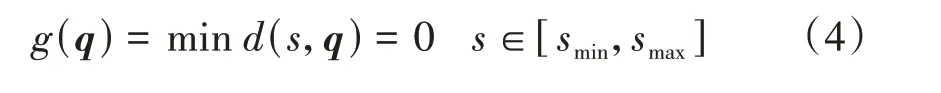
式中：[smin，smax]为车轮与钢轨廓形横坐标重合区域。

根据弹性力学原理，用数学方法将刚性接触模型的加权最小二乘近似与平滑项相结合得近似函数［10］，即准弹性接触条件为

式中：ε为对数应变系数，轮轨接触中取1 × 10-5～5 ×10-5，本文计算中取4 × 10-5；w(s，q) 为权重系数，w(s，q) = e-d(s，q)/ε，由d(s，q) ≥0可得w(s，q) ∈[0，1]。

准弹性修正后横向上的位置坐标为

刚性接触点经准弹性修正后即为准弹性接触点。

3 轮轨接触几何分析

3.1 轮轨接触点分布

利用法向切割法分别计算地铁标准和磨耗LM 踏面与9号道岔尖轨尖端及尖轨顶宽20、35、50 mm 断面匹配且轮对横移量b从-12.0 mm 变化到12.0 mm 时的轮轨接触点分布，不考虑摇头角。结果见图3。

图3 LM踏面与9号道岔不同断面匹配时轮轨接触点分布

由图3可知：

1）与尖轨尖端匹配时，磨耗LM 踏面刚性接触点跳跃明显，准修正后接触点更平滑连续，最大修正量为3.18 mm；标准LM 踏面在车轮向负方向发生横移时，准弹性接触点相较于刚性接触点有明显修正，b=-12.0 mm时最大修正量为2.60 mm。

2）与尖轨顶宽20 mm 断面匹配时，随轮对横移量增大，轮轨接触点由基本轨过渡到尖轨上。①对于标准LM 踏面，准弹性接触点与刚性接触点相比，由基本轨跳跃至尖轨前后有明显修正。跳跃前，b= 7.5 mm时，准弹性接触将基本轨上接触点向尖轨方向修正，修正量为7.30 mm；b=8.0 mm 时接触点跳跃至尖轨，尖轨上接触点向基本轨方向修正，修正量为6.62 mm。②对于磨耗LM 踏面，b= 9.5 mm 时刚性接触点已过渡到尖轨上，而准弹性接触点还在基本轨上，准弹性接触点较刚性接触点更晚发生轮载过渡。

3）与尖轨顶宽35 mm 断面匹配时，标准LM 踏面所有接触点已转移至尖轨上；而磨耗LM 踏面接触点在b= 6.0 mm 时才从基本轨跳跃至尖轨上。对于标准LM 踏面，准弹性接触点较刚性接触点更为平滑，在b= 5.0 mm 时最大修正量为2.47 mm。对于磨耗LM踏面，发生跳跃前，b=5.5 mm 时，准弹性接触将基本轨上接触点向尖轨方向修正，修正量为6.62 mm；b=6.0 mm 时，接触点跳跃至尖轨，尖轨上接触点向基本轨方向修正，修正量为12.81 mm。

4）与尖轨顶宽50 mm 断面匹配时，标准及磨耗LM 踏面轮轨接触点已经全部转移至尖轨上，且准弹性修正前后变化规律与尖轨尖端类似。

标准LM 踏面与9 号道岔匹配时轮轨接触点随轮对横移量的变化较均匀。磨耗后LM 踏面与9 号道岔匹配时，轮对横移向左时，轮轨接触点向非工作边偏移，且轮轨接触点跳跃较大，车轮磨耗明显改变轮轨接触点状态，使轮轨接触点向外侧移动，并加剧轮轨接触点的跳跃性和不连续性。经过准弹性修正后的接触点，由于考虑了一定轴重下轮轨接触区域的弹性变形，能在一定程度上改善轮轨接触点的跳跃性，使接触点更加均匀连续，甚至会改变轮载过渡的位置。

3.2 道岔转辙器的结构不平顺

道岔转辙器区由于尖轨和基本轨的组合廓形随纵向里程不断变化，存在固有结构不平顺。计算时选取的特征断面顶宽间隔约3 mm。标准车轮与磨耗车轮过道岔转辙器时，准弹性修正前后钢轨接触点结构不平顺随尖轨顶宽的变化曲线见图4。

图4 钢轨接触点结构不平顺随尖轨顶宽的变化曲线

由图4可知：

1）在轮载过渡前，钢轨横向不平顺随尖轨顶宽增大而增大，最大可达31～38 mm；在轮载过渡时横向不平顺产生突变，突变后在0 附近波动。对中状态下过岔，标准LM 踏面在尖轨顶宽32 ～ 35 mm 实现轮载过渡。磨耗LM 踏面横向不平顺的最大值较标准LM 踏面大，其突变位置的尖轨顶宽也变大。这是由于车轮磨耗后，对中状态下轮轨接触点位置发生变化，轮载过渡位置也向后偏移。对标准LM 踏面，准弹性修正后横向不平顺在达到最大值后有一定程度的降低，而后产生突变；对于磨耗LM 踏面，修正前后横向不平顺变化趋势基本一致，轮载过渡后，修正后的横向不平顺波动值趋近0。

2）钢轨竖向不平顺较小，不超过1.3 mm。在轮载过渡前钢轨接触点位置在竖向上变化不大，轮载过渡时轮轨接触点位置突然降低，然后又迅速升高，磨耗前后车轮踏面均在顶宽50 mm后维持较小波动。

3.3 轮轨接触角差

轮轨接触角会影响轮轨蠕滑力的分配，进而影响轮轨磨耗、接触疲劳伤损等。轮轨接触角差随轮对横移的变化曲线见图5。

图5 接触角差随轮对横移量的变化曲线

由图5可知：

1）与尖轨尖端匹配时，踏面接触时接触角差随轮对横移量的变化相对较小；轮缘接触后接触角差急剧增至1.2～1.3 rad；随着轮对横移量继续增大，接触角差降至0.9 ～ 1.0 rad。踏面接触时，准弹性修正后的接触角差略小于修正前，轮缘接触后基本一致。

2）与尖轨顶宽20 mm 断面匹配时，轮载过渡前接触角差随轮对横移量的变化相对较小。轮轨接触点由基本轨转移至尖轨时，对于刚性接触，接触角差会发生台阶式跳跃，增至0.33 rad左右，之后随轮对横移量增大而小幅增大，直到发生轮缘接触，接触角差迅速增至1.20 rad以上。在刚性接触角差随轮对横移量出现台阶式变化位置，准弹性修正后的接触角差明显更平滑连续。

3）与尖轨顶宽35 mm 断面匹配时，对于标准LM踏面，轮轨接触角差随轮对横移量的变化规律与尖轨尖端工况类似。这是因为在顶宽35 mm 处轮轨接触点已完全从基本轨转移至尖轨，随着轮对横移量增大，由车轮踏面接触转变为轮缘接触。对于磨耗LM踏面，轮轨接触角差随轮对横移量的变化规律与尖轨顶宽20 mm工况类似。

4）与尖轨顶宽50 mm 断面匹配时，两种车轮踏面轮轨接触点均已过渡到尖轨上，轮轨接触角差变化规律与尖轨尖端工况类似。

3.4 滚动圆半径差

轮轨接触的滚动圆半径差是求解等效锥度的重要参数，能在一定程度上反应轮对的动态特性。轮对横移量从0变化到12 mm 时滚动圆半径差的变化曲线见图6。可知：轮缘接触前，随轮对横移量增大，滚动圆半径差增幅较小；发生轮缘接触后，滚动圆半径差迅速增大；在尖轨顶宽20 mm 处，随轮对横移量增大，轮载过渡前滚动圆半径差变化较小，轮载过渡处刚性滚动圆半径差出现跳跃，经准弹性修正后滚动圆半径差更连续；在尖轨顶宽35 mm 处，对磨耗LM 踏面，滚动圆半径差变化规律与尖轨顶宽20 mm处类似。

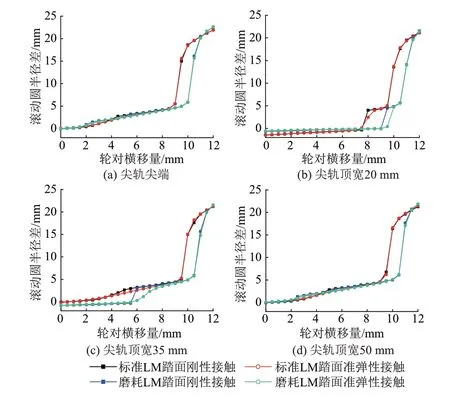
图6 滚动圆半径差随轮对横移量的变化曲线

3.5 等效锥度

等效锥度是表征轮轨接触几何特征的重要参数，直接反映轮轨之间的匹配程度。目前常用的等效锥度计算方法有简化法、谐波法、UIC519 法等。UIC519法采用随机运动假设，在对磨耗车轮进行计算时更准确［12］，所以本文采用UIC519标准计算等效锥度。

等效锥度随轮对横移量的变化曲线见图7。

图7 等效锥度随轮对横移量的变化曲线

由图7可知：

1）标准LM 踏面和磨耗LM 踏面与尖轨尖端、尖轨顶宽50 mm 断面匹配时，在轮对横移量较小情况下，准弹性修正后的等效锥度略大于刚性等效锥度；轮对横移量增至一定值后，准弹性等效锥度明显小于刚性等效锥度，且等效锥度随轮对横移量的变化率更小。

2）与尖轨顶宽20 mm 断面匹配时，等效锥度最大值出现在横移量较小的情况下；随横移量增大，等效锥度总体呈减小趋势；准弹性修正后的等效锥度最大值比刚性等效锥度的最大值要小，变化更平缓。

3）与尖轨顶宽35 mm 断面匹配时，标准LM 踏面修正前后的等效锥度变化规律与尖轨尖端工况类似；磨耗LM 踏面的等效锥度随横移量的增大先大幅降低，而后平缓增大。准弹性修正后的等效锥度最大值明显低于刚性等效锥度，准弹性等效锥度变化曲线更平缓。这是因为准弹性接触是考虑了轮轨间弹性变形的简化算法，能在一定程度上修正刚性接触算法下轮轨接触的跳跃性，使准弹性接触法下等效锥度反映出的轮轨匹配特性更好。