汽车后雨刮器齿轮连杆机构非线性动态性能分析

聂子枫，陈燚涛*，苏工兵，陈俊宇，胡继文

汽车后雨刮器齿轮连杆机构非线性动态性能分析

聂子枫1，陈燚涛*1，苏工兵1，陈俊宇1，胡继文2

(1. 武汉纺织大学 机械工程与自动化学院，湖北 武汉 430200；2.武汉思凯精冲模具有限公司，湖北 武汉 430000)

为解决汽车后雨刮齿轮连杆机构运行不稳定、噪音大等问题，建立了齿轮连杆机构系统非线性动力学模型，并以齿侧间隙、外部动态激励等为控制参数，利用MATLAB/SIMULINK对连杆齿轮非线性动力学模型进行数值仿真。结果表明，随着齿侧间隙不断增大，系统由2周期响应过渡到4周期响应，系统动载荷幅值先减小后增大，机构系统也趋于不平稳状态；随着输入转矩不断增大，系统由2周期响应逐渐过渡到混沌，系统动载荷幅值增大，当输入转矩过大时，机构系统变为混沌状态。由此在控制齿侧间隙、外部动态激励在某一范围，能有效的控制齿轮系统的非线性振动响应。该研究成果为齿轮连杆机构设计制造和安装以及参数优化提供了理论支撑。

汽车后雨刮器；齿轮连杆机构；齿轮啮合动态特性

0 引言

齿轮连杆机构是汽车后雨刮传动组件的关键传动装置，其主要作用是实现运动转换和刮擦角度的放大，其力学行为和工作性能直接影响了汽车后雨刮器的整体性能。一旦齿轮连杆组件齿轮设计不合理或者装配过程存在较大误差时，会导致后雨刮器运动状态不平稳，甚至产生运动卡滞以及较大运动噪音，最终可能导致后雨刮器性能不稳定、寿命降低。特别是在新能源电动汽车里，运动噪音在安静环境下会进一步放大，引起客户投诉。因此需要从理论上对齿轮连杆机构进行动态特性的分析。

齿轮连杆机构运动性能是一个非线性动力学问题，国内外学者已对齿轮非线性动力学模型建立及计算方法已经展开了大量的研究工作[1-4]，Kahraman等[5]基于谐波平衡方法对时变啮合刚度、齿侧间隙和误差激励之间的相互作用及其对齿轮系统动态性能进行研究。Li等[6]建立了含新的间隙函数的齿轮动力学模型，并研究了该系统的动态特性。Huang等[7]考虑了动态响应与表面粗糙度的间接关系，研究了齿轮系统动态性能，这些研究为解决齿轮连杆机构不平稳运行的问题奠定了基础。

本文在对一种汽车后雨刮器齿轮连杆机构分析建模的基础上，采用MATLAB/SIMULINK仿真分析了在外部动态激励作用下的不同齿轮间隙、激励幅值对连杆齿轮系统动力学特性的影响，为汽车后雨刮器齿轮连杆机构的优化设计奠定了基础。

1 对象分析及模型简化

1.1 对象分析

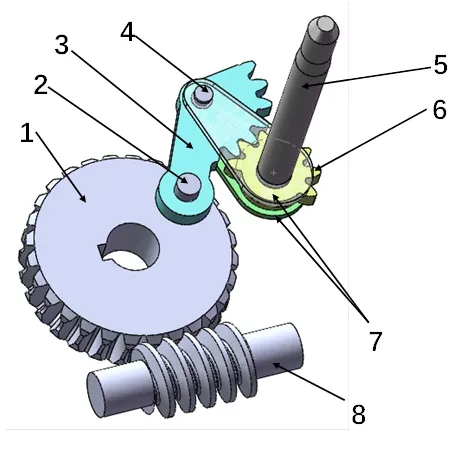
1蜗轮；2圆柱销；3大齿轮；4台阶销；5输出轴；6小齿轮；7连接板；8蜗杆

图1是汽车后雨刮器传动机构简图，蜗轮蜗杆作为一级传动，可以得到较大的传动比，其次由涡轮带动大齿轮转动，大齿轮和小齿轮为二级传动，齿轮传动实现换向和角度放大作用，最后由输出轴输出转矩和转角。

四连杆机构能实现机构的往复运动从而实现雨刮器的功能，在连杆机构上增加齿轮副为了实现刮擦角度放大。增加齿轮副后，机构运行过程中可能出现运动不平稳和噪音过大现象，产生此问题的原因是机构由四连杆驱动，四连杆具有急回特性，不完全齿轮副在换向的两个极限位置（如图2所示）因齿隙、外部激励、啮合刚度等综合因素，会导致齿轮相互冲击，最终导致机构运动不平稳，齿轮啮合冲击力变大而产生噪音。

图2 齿轮连杆机构极限位置

1.2 模型简化

通过分析，可以将汽车后雨刮器齿轮连杆机构简化成如图3的机构模型。

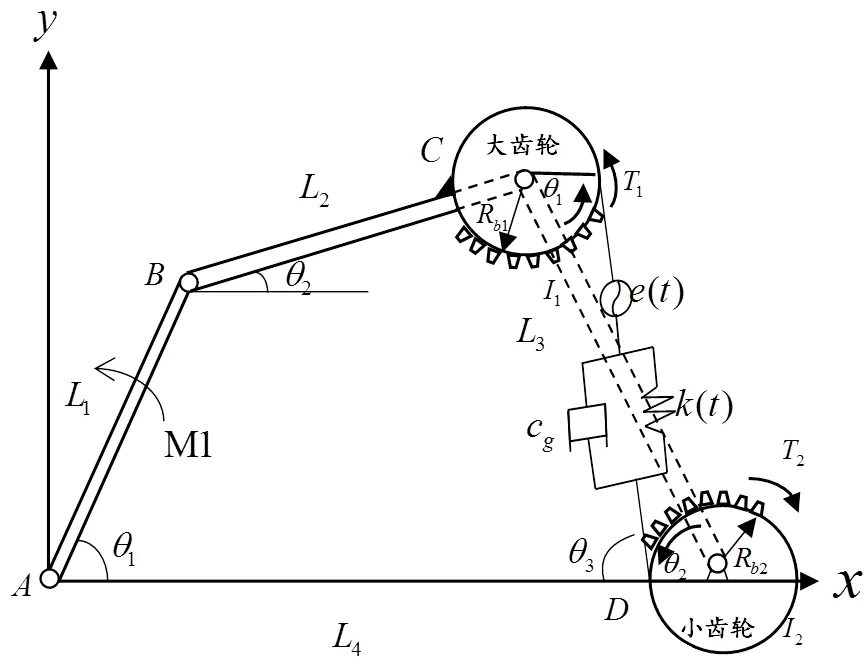
图3 汽车后雨刮器齿轮连杆机构简化示意图

简化示意图中，AB、BC、CD杆分别对应齿轮连杆机构中的蜗轮、大齿轮、连杆，杆BC与大齿轮为同一个构件，M1为电机提供的驱动力矩，M2为机构受到的负载力矩，其中M2的方向始终与CD杆的方向相反，且转动副C处的约束反力作为齿轮的外部激励，杆CD的长度为齿轮啮合中心距。

汽车后雨刮器传动机构是否稳定运行取决于大、小齿轮非线性接触是否平稳。而影响齿轮非线性接触有几个主要因素：外部激励（原动机输入扭矩）、内部激励（齿轮间隙）等。在此机构中蜗轮提供外部激励带动大齿轮转动，表1给出了一种汽车后雨刮器齿轮连杆机构的齿轮副设计参数。在连杆机构中，杆CD长度决定齿轮间隙大小，表2给出了该雨刮器各连杆机构的设计尺寸。

表1 一种汽车后雨刮器齿轮连杆机构齿轮副设计参数

表2 齿轮连杆机构设计尺寸参数

2 齿轮连杆机构非线性动力学建模

2.1 机构运动学分析

如图3所示，曲柄AB（L1），连杆BC（L2），摇杆CD（L3），机架AD（L4）。建立直角坐标系。

闭环矢量方程为：

则角位移方程的分量为：

相应得到角速度与角加速度方程并整理为矩阵形式：

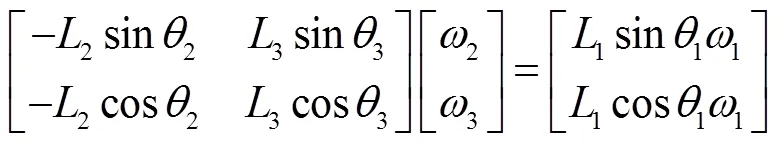
2.2 机构动力学分析

2.2.1 连杆系统动力学

对齿轮连杆机构中各连杆进行受力分析如图4.

图4 连杆机构各连杆受力分析

AB杆：

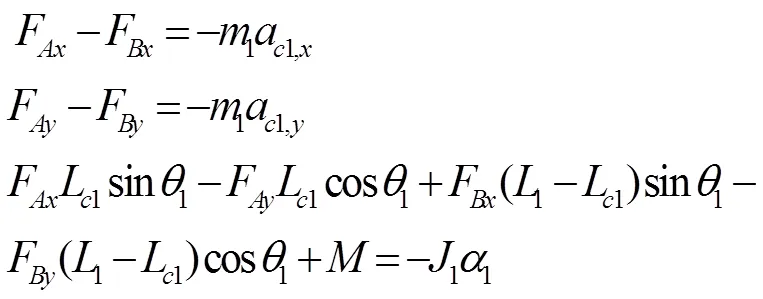
BC杆：

CD杆：

将式（5）、（6）、（7）整理成矩阵形 ：

其中：

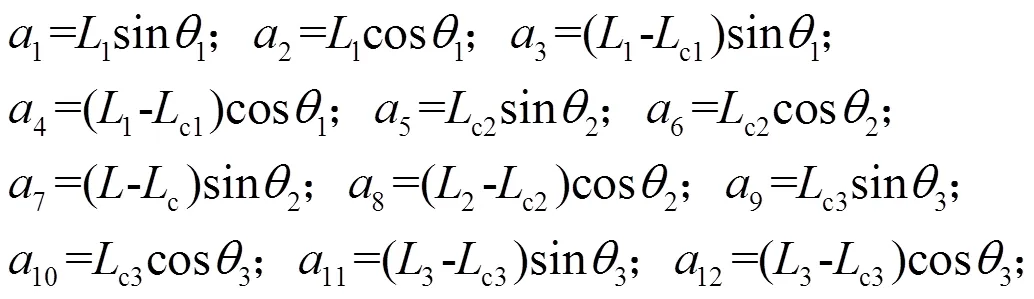
将式（8）中各杆的质心加速度的分量与机构的运动状态包括连接件位移、速度和加速度联系起来，矩阵形式为

2.2.2 齿轮系统动力学

对应动力学方程为：

由于齿轮啮合时，刚度的量纲为109，误差和间隙的量纲为10-6，量纲数量级相差较大，数值求解会产很大的误差，因此需要对系统进行量纲一化处理，引入齿轮啮合线上的相对位移作为广义坐标：

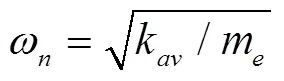
间隙非线性函数：

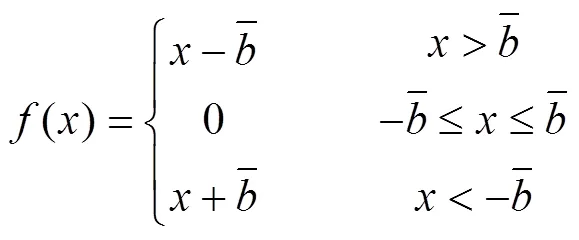
式（10）的量纲一化方程：

若刚度和轮齿综合误差均取一阶谐波分量，则有：

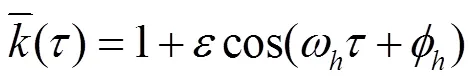
将式（11）转化为状态方程如下：

3 齿轮副换向点状态分析

图5 齿轮副换向点啮合状态简图

4 齿轮连杆机构SIMULINK建模

在Matlab/SIMULINK系统环境下，机构运动学仿真的时候各个模块均以正向关系为联接关系，但是在动力学仿真的时候各个板块是逆向联结关系。在图6中，仿真模型主要由4个函数模块、5个积分模块、2个输入模块和2个输出模块等组成。其中4个函数模块M_1.m、M_2.m、M_3.m分别是根据式（4）、式（9）和式（8）编写，M_4函数模块的作用是在连杆仿真后的输出信号里面取最大值，然通过量纲一化处理作为齿轮系统的外部激励进行齿轮系统仿真，所有机构参数必须定义在这个4个函数中。

图6 齿轮连杆机构SIMULINK仿真模型

5 参数对系统非线性振动特性的影响

5.1 齿侧间隙对系统非线性振动的影响

齿侧间隙计算公式：

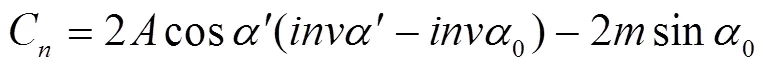
如图7所示为系统动载荷幅值随齿侧间隙的变化图，从图7可知：

图7 动载荷随尺侧间隙2b变化图

图8 2b=14系统动态响应

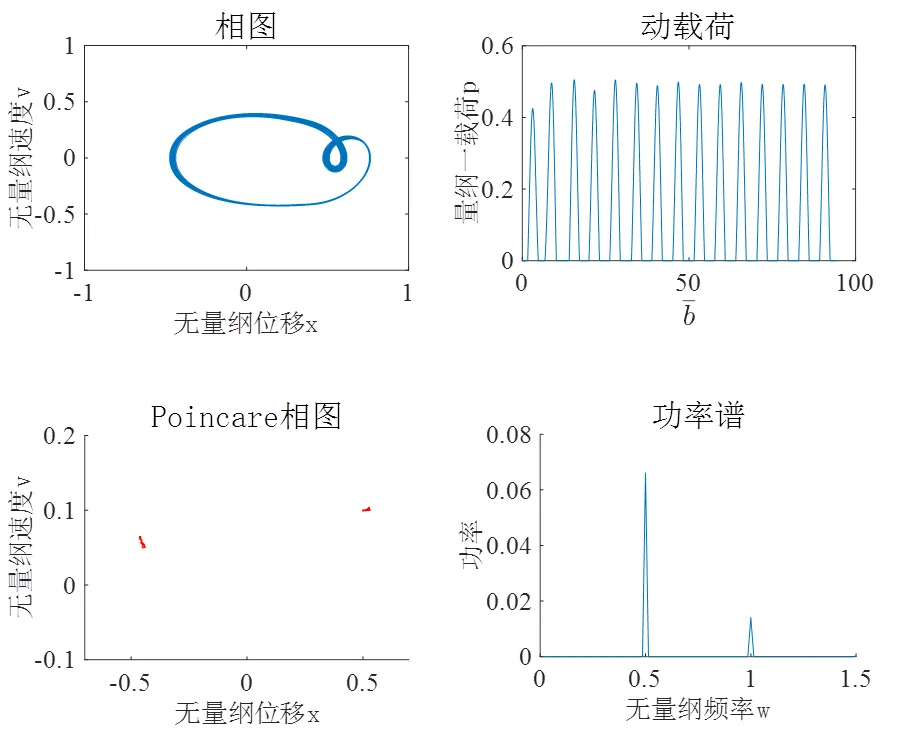
图9 2b=10.88系统动态响应

图10 2b=15.68系统动态响应

5.2 输入转矩对系统非线性振动的影响

如图11所示为系统动载荷幅值随输入转矩变化图，从图中可知:

图11 动载荷随电机输入转矩变化图

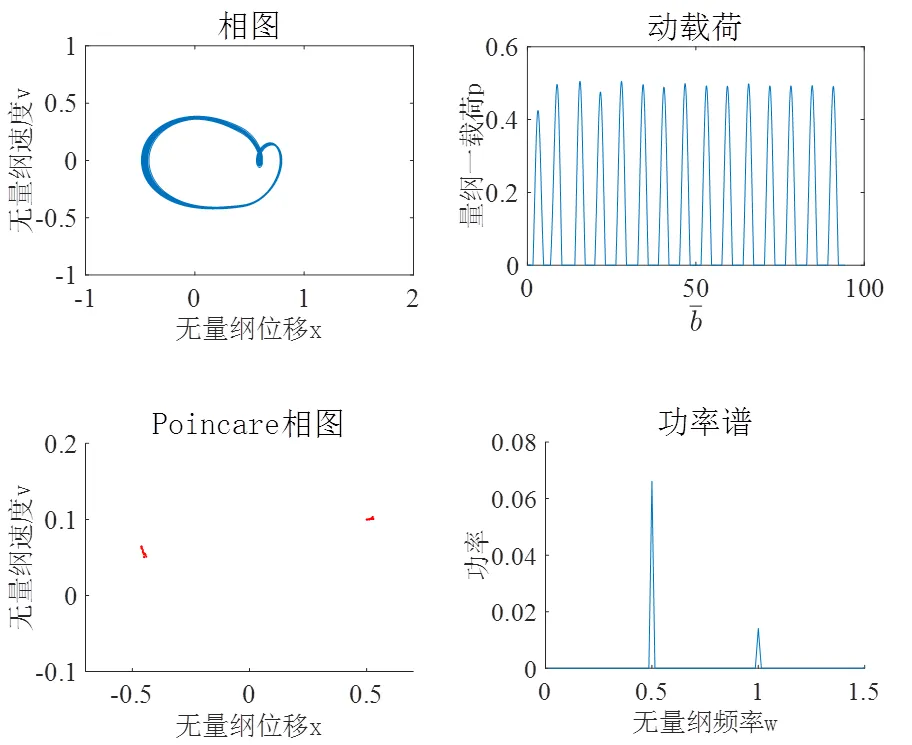
图12 转矩=2系统动态响应

图13 动载荷随电机输入转矩变化图

6 结论

（1）综合考虑外部激励、齿侧间隙等因素，建立齿轮连杆机构非线性动力学模型。

[1] 王建军, 李其汉, 李润方. 齿轮系统非线性振动研究进展[J]. 力学进展, 2005, (01): 37-51.

[2] Han L, Xu L, Qi H. Influences of friction and mesh misalignment on time-varying mesh stiffness of helical gears[J]. Journal of Mechanical Science and Technology, 2017, 31(7): 3121-3130.

[3] Yang B, Feng S, Tian J,et al. Investigation on the Nonlinear Dynamic Characteristics of the Air Lubricated Bearing Conceming Frequency of Perturbation Effect[C]. IEEE International Conference on Mechatronics and Automation (ICMA). IEEE, 2019.

[4] Ouyang T, Su Z , Li S, et al. Experimental and numerical investigations on dynamic characteristics of gear- roller- bearing system[J]. Mechanism and Machine Theory, 2019, 140:730-746.

[5] Blankenship G W , Kahraman A. Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type non-linearity[J]. Journal of Sound & Vibration, 1995, 185(5):743-765.

[6] Li Z, Peng Z. Nonlinear dynamic response of a multi- degree of freedom gear system dynamic model coupled with tooth surface characters: a case study on coal cutters[J]. Nonlinear Dynamics, 2015, 84(1):1-16.

[7] Xiong, Yangshou, Huang, et al. Research on the dynamic response of high-contact-ratio spur gears influenced by surface roughness under EHL condition[J]. Applied Surface Science A Journal Devoted to the Properties of Interfaces in Relation to the Synthesis & Behaviour of Materials, 2017，392: 8-18.

Analysis of the Nonlinear Dynamic Performance of the Gear-Link Mechanism of Automobile Rear Wiper

NIE Zi-feng1, CHEN Yi-tao1, SU Gong-bing1, CHEN Jun-yu1, HU Ji-wen2

(1. School of Mechanical Engineering; Wuhan Textile University, Wuhan Hubei 430200, China；2. Wuhan Sikai Fine Blanking Mould Co., Ltd., Wuhan Hubei 430000, China)

In order to solve the problems of unstable operation and loud noise of the rear wiper gear linkage mechanism of the automobile, a nonlinear dynamic model of the gear linkage mechanism system was established. And take the side clearance and external dynamic excitation as control parameters, and use MATLAB/SIMULINK to numerically simulate the nonlinear dynamic model of the connecting rod gear. The results show that with the continuous increase of the tooth side clearance, the system transitions from a 2-period response to a 4-period response. The dynamic load amplitude of the system first decreases and then increases, and the mechanism system also tends to be unstable; as the input torque continues to increase. The system gradually transitions from a 2-period response to chaos, and the dynamic load amplitude of the system increases. When the input torque is too large, the mechanism system becomes chaotic. Therefore, when controlling the tooth backlash and external dynamic excitation within a certain range, the nonlinear vibration response of the gear system can be effectively controlled. The research results provide theoretical support for the design, manufacture, installation and parameter optimization of the gear linkage mechanism.

car rear wiper; gear linkage; gear mesh dynamic characteristics

陈燚涛（1972-），男，教授，硕士生导师，研究方向：精冲技术与精冲模具.

U463.212

A

2095－414X(2022)01－0020－06