卵形弹丸对混凝土侵彻动力响应数值研究
2022-03-05朱少平王志亮
朱少平, 王志亮, 熊 峰
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
混凝土作为当今最主要的土木工程建筑材料,其在安全与防护领域应用广泛,混凝土结构在高速冲击下的动力响应是当前研究的热点。
文献[1]通过高速弹体对混凝土拱形靶体的侵彻数值模拟,分析不同拱形靶体的侵彻效应;文献[2]基于LS-DYNA有限元软件对混凝土靶空腔响应区域进行识别划分,获得了侵彻过程中混凝土各响应区的区域大小;文献[3-4]研究混凝土中自由水含量对靶体侵彻性能的影响,指出自由水含量提高会提升靶体抗侵彻性能;文献[5]进行C60混凝土侵彻试验,并与已开展的C35混凝土侵彻试验结果对比,认为随混凝土强度等级提高,混凝土表面破坏越大,弹丸过载及侵蚀程度越高;文献[6-7]开展不同厚度混凝土靶体侵彻试验及数值模拟,得到靶板单位耗能和靶背影响区与靶板厚度成正相关的规律;文献[8]通过控制子弹速度为800~900 m/s侵彻中等强度混凝土,发现子弹侵彻斜角越大,越不利于侵彻,且弹丸延性导致的侵彻变形是造成侵彻失效的主要原因。
以上研究工作主要集中于混凝土结构形式、强度、自由水含量及子弹打击角度等因素对混凝土侵彻性能的影响,且主要涉及对最终结果的讨论,而对于混凝土侵彻中弹丸形状系数效应研究较少,且测量结果往往只包含初始和最后状态数据,对于整个侵彻过程的分析缺乏有效的数据验证。本文基于AUTODYN有限元软件,运用SPH-Lagrange耦合方法,对不同弹丸形状系数及速度下靶板侵彻损伤与动力响应开展分析,并设计正交实验探究混凝土本构模型参数对贯穿剩余速度的敏感性,力求得出具有参考价值的结论。
1 混凝土损伤RHT本构模型
根据文献[9]的研究,混凝土的抗压和抗拉强度与应变率密切相关。文献[10]在Holmquist-Johnson-Cook (HJC) 本构模型基础上提出了Riedel-Hiermaier-Thoma (RHT) 本构模型,除了考虑屈服面的压力依赖性外,RHT本构模型还考虑了压力硬化、应变硬化、应变速率硬化、偏应力第三不变量及应变软化。RHT本构模型已广泛应用于混凝土材料在冲击载荷作用下的动力特性分析[11],包括强度模型和损伤模型,通常与p-α状态方程一起使用。
1.1 状态方程
p-α状态方程[12]可用于详细描述材料在低应力下的压实过程以及高应力下所表现出来的符合实际情况的性能,其方程式如下:
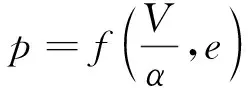
(1)
(2)
其中:V为多孔材料的比容;α、αp分别为孔隙度及弹性屈服孔隙度;e为初始内能;ps、pe分别为孔隙压实对应的压力和材料弹性屈服对应的压力;n为孔隙度指数。
1.2 强度面方程
RHT模型有3个与压力相关的强度面,分别为弹性极限面、失效强度面及残余强度面。失效应力、弹性极限应力及残余应力具体表达式[13]如下:
(3)
(4)
σr=B(p*)M
(5)
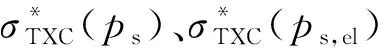
1.3 损伤模型
损伤变量D为累积等效塑性应变增量与最终失效等效塑性应变的比值(0≤D≤1),即
(6)
其中:D1、D2为材料的损伤参数;Δεp为等效塑性应变变化量;εfmin为最小失效应变;T*为材料归一化拉伸强度,T*=T/fc,T为材料拉伸强度。
2 侵彻试验结果模拟验证
混凝土在冲击作用下表现的性质十分复杂,主要原因在于在此过程中通常会涉及3类非线性问题:几何非线性、材料非线性及边界非线性[14]。本文采用混凝土RHT本构模型,运用SPH-Lagrange耦合方法,对文献[7]所做的试验进行模拟和比较。
2.1 模型介绍
数值分析采用的侵彻模型尺寸与试验尺寸相同。其中混凝土为圆柱靶体,fc=45.5 MPa,直径D=1 800 mm,厚度H分为3种,即600、800、1 000 mm ;弹丸长度L=300 mm,长径比为5,卵形弹丸形状系数为3。考虑模型的对称性,数值模拟中取1/2模型进行计算。
根据文献[15]的研究,子弹侵彻岩石类介质材料,当子弹速度小于900 m/s,子弹可视为刚体;混凝土在冲击作用下局部产生大变形,采用Lagrange算法时,其网格随着子弹的侵彻产生严重的畸变,会使计算时间增大,部分情况可能导致计算不收敛。因此,本文模拟时针对子弹采用Lagrange算法,针对混凝土靶板采用光滑粒子流体动力学(smoothed particle hydrodynamics, SPH) 方法。由于SPH计算耗时长,且在小变形
时,采用Lagrange算法的网格精度可满足要求且计算效率高,因此在侵彻影响较大区域使用光滑粒子,在影响较小区域使用Lagrange算法。
试算后侵彻影响较大区域范围取5倍弹丸半径,对于影响较小区域,网格大小依据文献[16]给出的网格取值划分,即靶板网格尺寸为弹丸半径的1/6,靶板粒子与网格大小一致,均为5 mm。
2.2 RHT参数
根据文献[17],取混凝土剪切模量G=13.8 GPa,混凝土抗拉强度ft依据美国混凝土协会提出的关系式[18]进行计算,即
(7)
压缩应变率指数βc和拉伸应变率指数βt按RHT理论公式进行计算,计算公式为:
βc=4/(20+3fc)
(8)
βt=2/(20+fc)
(9)
其余参数在原始参数基础上调整,并以第1组试验的剩余速度为标准通过大量数值计算进行标定,最终RHT主要参数取值见表1所列。

表1 RHT模型主要参数
强度比;BQ为脆韧转变系数;gt*、gc*分别为拉伸、压缩屈服面参数。
2.3 模拟验证
文献[7]开展的3组试验中,前2组混凝土靶体厚度分别为600、800 mm,子弹穿靶后仍有剩余速度;第3组靶体厚度为1 000 mm,子弹最终未能穿透而留在靶内。本文以厚度H=600 mm靶体贯穿试验为例分析混凝土的侵彻过程。质量为4.15 kg的弹丸以试验弹速vi=639.9 m/s对混凝土靶进行冲击,其损伤演化过程如图1所示。
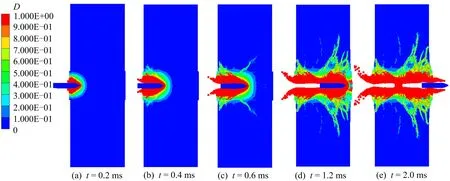
图1 H=600 mm靶体损伤演化过程
子弹高速冲击靶体,与靶体接触瞬时形成高压区,当接触时的应力大于混凝土动态强度时,混凝土主要受到压剪作用,形成“前坑区”,t=0.2 ms时子弹弹头完全侵入混凝土中;随着子弹侵彻深度增加,逐渐形成稳定的“隧道区”,此时冲击波不断向前传递,当冲击波传递到靶板背面时,经自由面的反射形成拉应力,由于混凝土抗拉强度远低于其抗压强度,t=0.6 ms时混凝土在拉应力作用下开始形成拉伸破坏裂纹,且其裂纹随着侵彻深度增加不断扩大;最终在t=2.0 ms时混凝土靶体形成完整的贯通隧道,此时“后坑区”的损伤范围已经趋于稳定。
为了评价数值模拟的准确性,选择子弹剩余速度和侵彻深度作为与试验对比的标准,剩余速度和侵彻深度相对误差δ1、δ2计算公式分别为:
(10)
(11)
其中:vr为试验剩余弹速;h为试验侵彻深度;vrs、hs分别为模拟的剩余弹速、侵彻深度。
H=1 000 mm靶体侵彻破坏状态与模拟损伤对比如图2所示。

图2 H=1 000 mm靶体破坏损伤试验与模拟情形对比
剩余速度和侵彻深度数据及误差分析见表2所列。
由表2、图2可知,SPH-Lagrange耦合方法能较好地对混凝土侵彻与贯穿进行模拟,其模拟最大误差不超过15%,损伤模拟结果与实际破坏状态基本相符。因此,本文采用SPH-Lagrange耦合方法模拟混凝土侵彻及贯穿是可行且有效的。

表2 靶体损伤模拟误差分析结果
3 混凝土侵彻动力响应
国内外的混凝土侵彻试验中子弹多为卵形弹,卵形弹形状系数(caliber radius head)定义为弹丸头部的曲率半径s与弹丸直径d的比值(一般为3~5)[19],即
(12)
为了研究混凝土在不同ψ下的动力响应,控制不同弹速使得子弹贯穿或留在靶体内,以此分析子弹的剩余速度分布规律及混凝土的动力响应。
3.1 不同ψ下混凝土非贯穿动力响应分析
根据子弹最终是否穿透靶体可以将侵彻分为贯穿和非贯穿过程。控制子弹的初始侵彻速度为vi=400 m/s,以使其打击时不穿透靶体,据此分析不同ψ下靶体非贯穿动力响应。数值模拟使用的子弹半径为30 mm,长度为300 mm,其ψ取值分别为3、4、5;混凝土靶半径为900 mm,厚度为600 mm。
混凝土靶体网格大小及粒子大小均为5 mm。侵彻过程结束时损伤的最终状态如图3所示,模拟侵彻深度hs及底部径向裂纹分布最大直径d′见表3所列。

图3 不同ψ下侵彻损伤分布状态
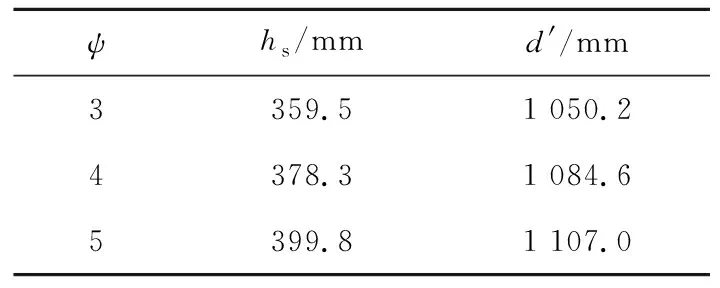
表3 vi=400 m/s时不同ψ下侵彻损伤对比
从表3可以看出:随着ψ增加,在不考虑子弹变形及质量损失情况下,hs增加,这与文献[20]的试验结果一致;d′与ψ成正相关。
为了详细研究侵彻过程中混凝土的动力响应,以ψ=3为例,在混凝土侵彻模拟过程中设置5个测点(1#~5#)观察混凝土内部动力响应,1#测点设置在靶体厚度1/2处,距对称轴100 mm,其他相邻测点间距为100 mm,测点布置如图4所示。
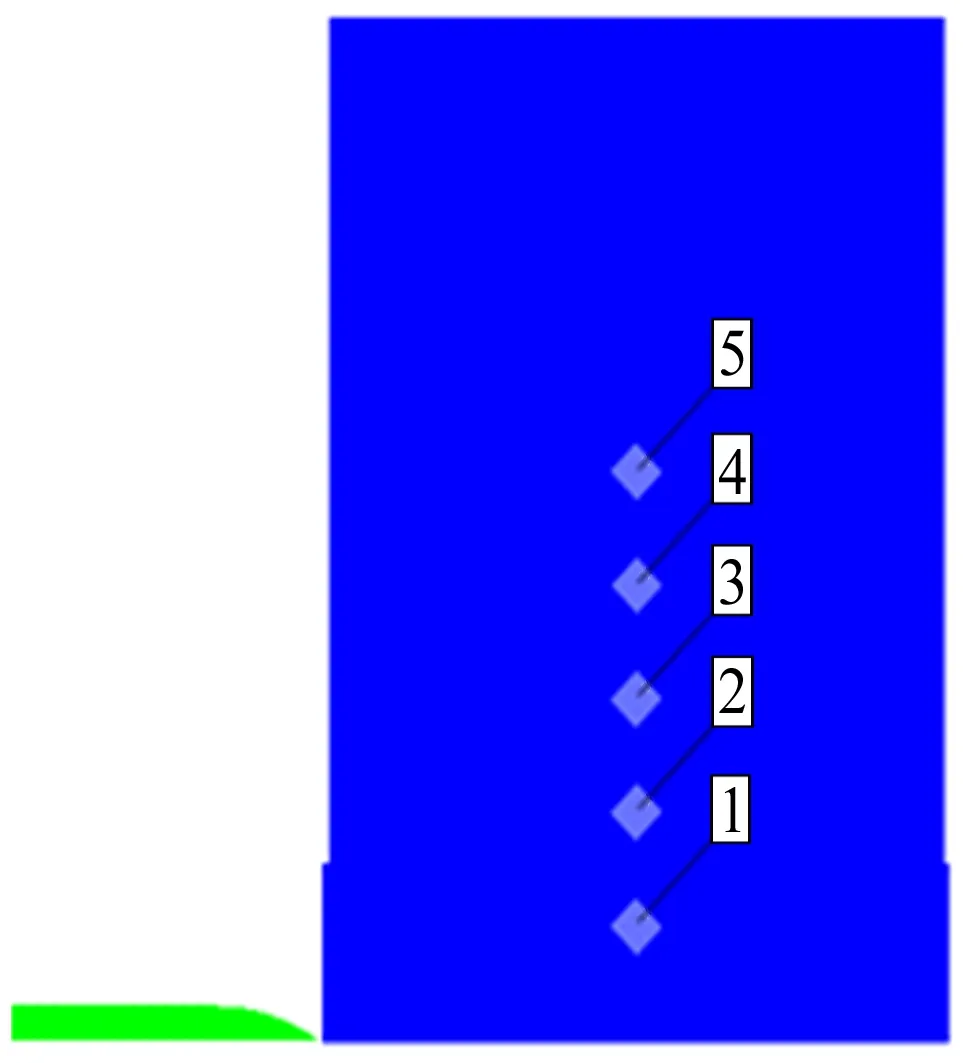
图4 测点示意图
5个测点在侵彻过程中速度、加速度变化时程曲线如图5所示。从图5可以看出:由近及远,最大速度依次减小,且1#、2#测点间振速之差远大于其他相邻测点差距,这说明侵彻过程中,近区混凝土受到的扰动很大,而距离稍远(如距中心点200 mm处后)所受到的扰动较小,混凝土振速在100~200 mm区间衰减最快;加速度曲线中,1#测点加速度最大值为14 468g,而2#测点加速度最大仅为7 005g,其最大加速度衰减1/2,这也印证了在2#测点后混凝土产生的动力响应较小。本文的耦合范围取150 mm,这既能反映混凝土在此范围产生的较大动力响应,又可以减小SPH粒子的布置区域,在保证模拟精度的条件下大大提高了计算效率。
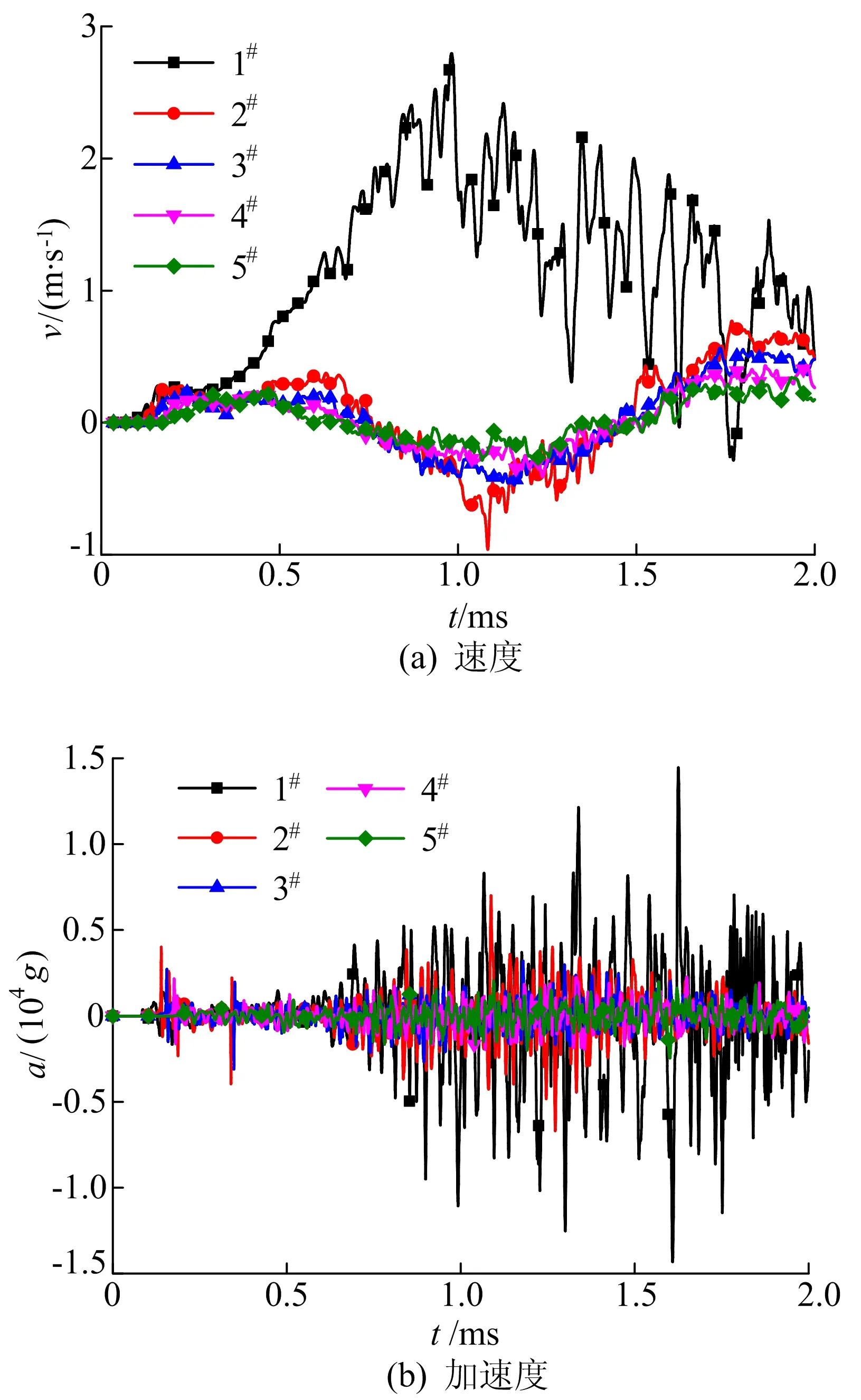
图5 5个测点速度、加速度变化时程曲线
3.2 不同ψ下混凝土贯穿动力响应分析
保持子弹及混凝土尺寸与上述侵彻分析一致,调整vi=600 m/s,使得子弹在冲击时贯穿混凝土靶体后仍具有一定的剩余速度,从而分析剩余速度分布规律及混凝土的动力响应。
由前述分析可知,随着ψ增大,尖端部分越长,相应子弹质量越小,相同速度下,子弹的初始动能也越小。vi=600 m/s时不同ψ下子弹速度时程曲线如图6所示。虽然ψ=3对应的初始动能最大,但从图6可以看出,其最终贯穿混凝土的剩余速度最小。其原因主要是ψ=5子弹整体形状最尖,在子弹冲击混凝土过程中,由于作用面积小导致其产生的应力更大,弹体在侵彻过程中更容易排开混凝土材料,因此侵彻过程也发展较快,最终子弹贯穿后剩余速度最大。
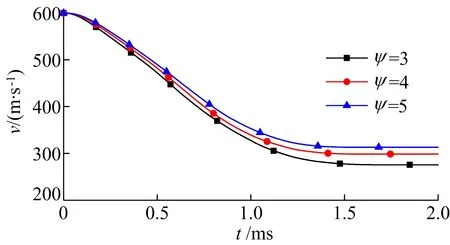
图6 vi=600 m/s时不同ψ下子弹速度时程曲线
不同ψ下混凝土1#测点的振速时程曲线如图7所示。
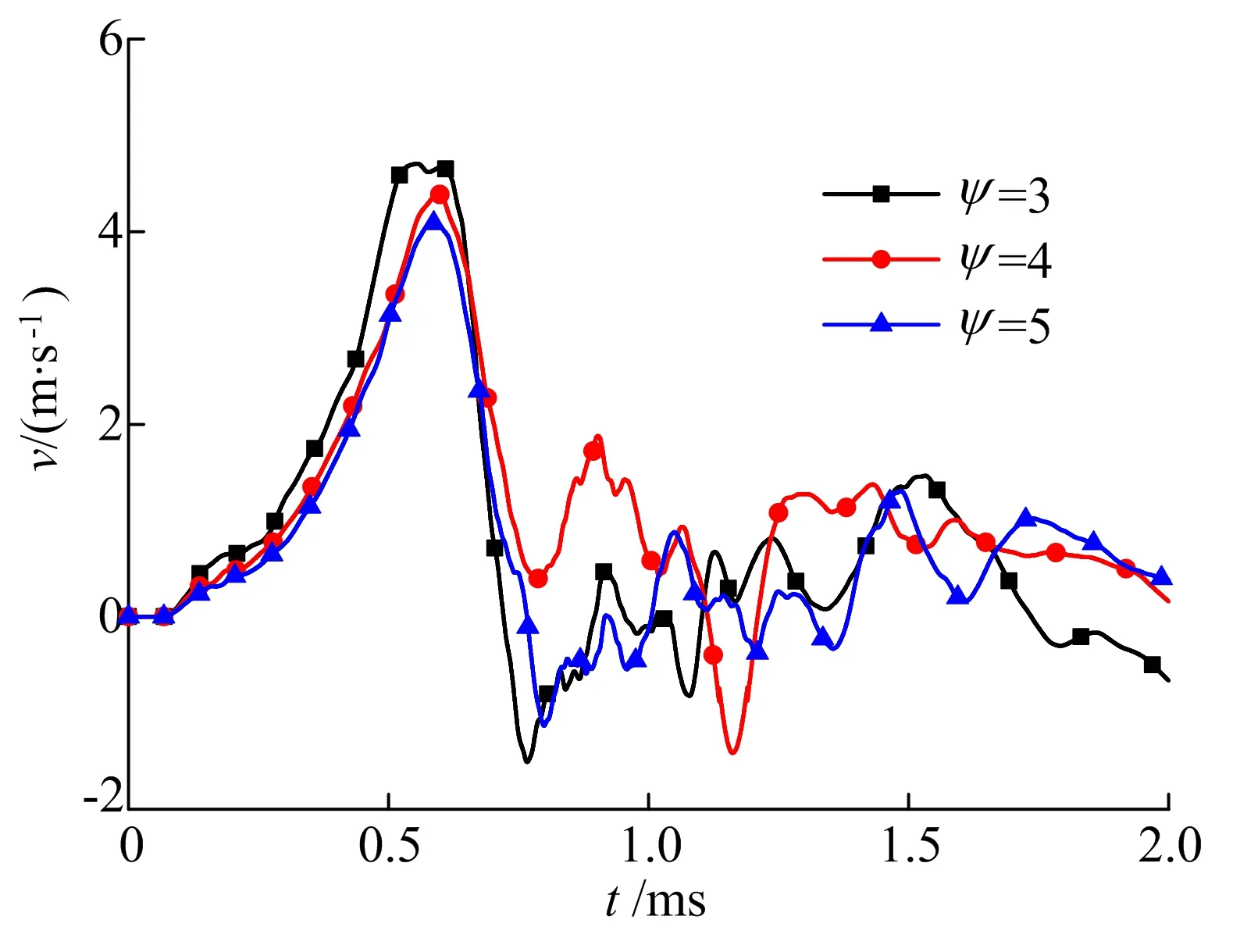
图7 不同ψ下混凝土1#测点的振速时程曲线
由图7可知,ψ为3、4、5引起1#测点最大振速分别为4.70、4.39、4.09 m/s。由前述分析可知,ψ=3弹丸在侵彻过程中损失动能最大,其次为ψ=4弹丸,而弹丸损失的动能用于贯穿混凝土,并在此过程中引起混凝土的动力响应。从1#测点最大振速及振速时程曲线可以看出,ψ=3引起混凝土动力响应最大,也因此耗散较多的动能。
4 RHT本构模型参数敏感性分析
影响数值模拟结果的原因主要分为模型简化的正确性和材料参数的准确性2个方面。其中,材料本构模型参数的选取影响模拟结果的精度。本构模型参数的敏感性分析是指研究单个或部分参数改变引起模拟结果变化大小。本文通过正交实验设计对选用的混凝土RHT本构模型参数敏感性进行分析。
4.1 正交实验设计方案
正交实验设计目的是考察多个因素对实验指标影响程度以及如何有效地减小实验次数,同时获取足够多的信息,进而对实验数据进行有效分析[21]。由于RHT本构模型参数多,采用正交实验进行分析,能够有效提高计算效率。
本文选取考察的因素指标数总计13个,设为3个水平,其中水平2为本文使用的部分参数取值,水平1和水平3的参数取值在水平2基础上遵循正交实验设计原则进行调整,符合常用混凝土RHT本构模型参数取值,具体参数水平取值见表4所列。

表4 RHT本构模型参数正交实验3种水平下的取值
由因素数和水平数选择正交设计表L27(313),此次正交实验结果以子弹贯穿时的剩余速度为评判标准。
子弹长径比和质量与前述一致,ψ=3,vi=600 m/s;混凝土靶体厚度为600 mm,半径为900 mm;弹体及靶体网格划分和前述一致,靶体仍使用SPH-Lagrange耦合方法。正交实验设计及子弹剩余速度见表5所列。

表5 正交实验设计方案及实验结果
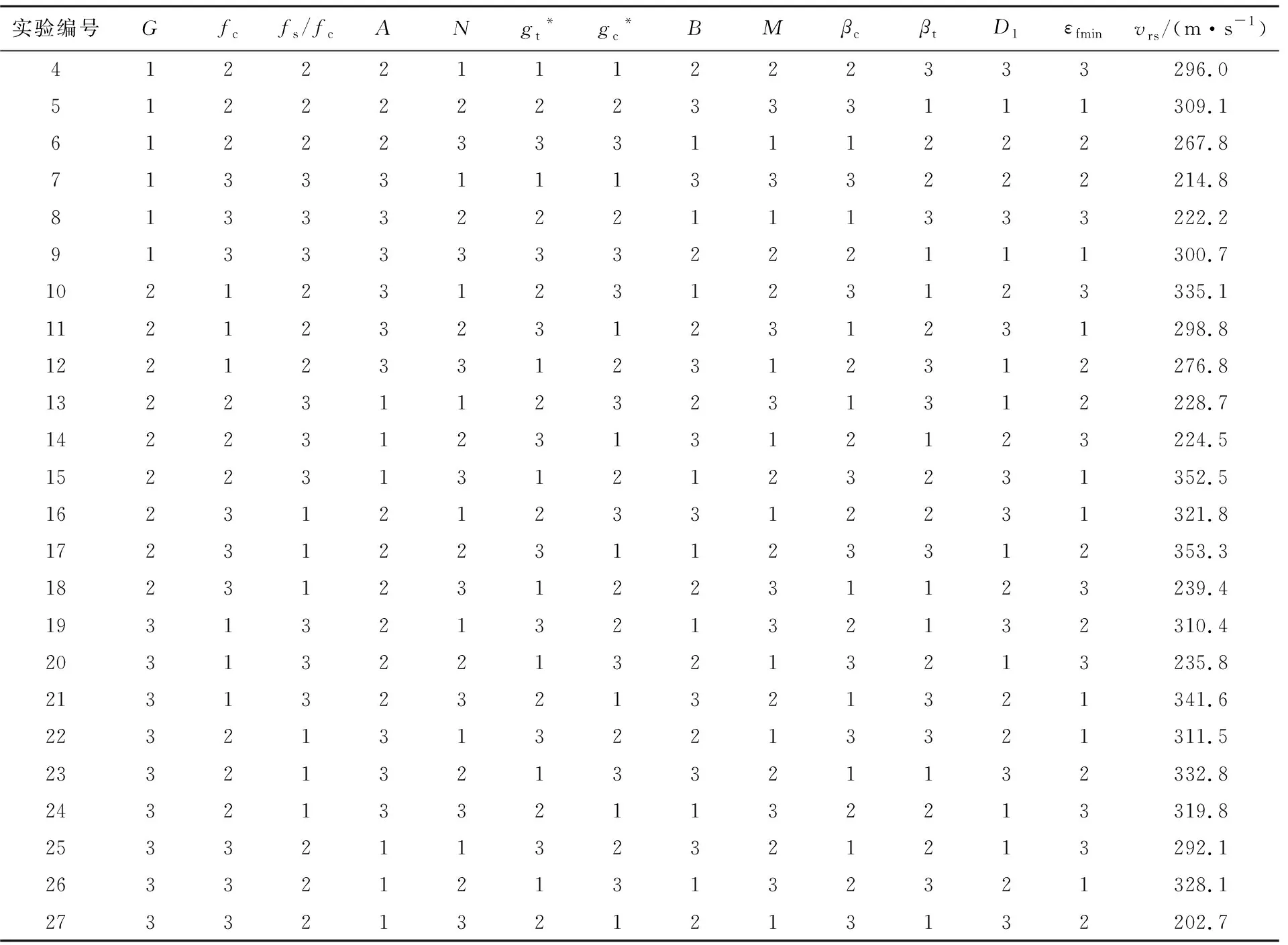
续表
4.2 仿真计算结果分析
在进行27组试验后,获得在相同子弹和靶体模型下,不同混凝土本构模型参数下的剩余速度,并以此为标准进行直观分析。
最后得到各参数在不同水平下vrs平均值和极差,见表6所列。

表6 各参数3个水平下vrs均值和极差分析结果 单位:m/s
极差指标的大小反映各因素水平改变对实验结果的影响程度,即参数敏感性。从表6可以看出,fc、fs/fc、B、M和εfmin参数极差均超过40.0且远大于其他参数极差。因此,fc、fs/fc等强度指标在混凝土侵彻中敏感性高,且残余强度面参数B、M敏感性均高于失效强度面参数A、N;εfmin对最终的实验结果影响也较大。根据上述分析,将参数敏感性分为2个等级,较为敏感参数为fc、fs/fc、B、M、εfmin,相对不敏感参数为G、A、N、gt*、gc*、βc、βt和D1。各因素指标效应曲线如图8所示。
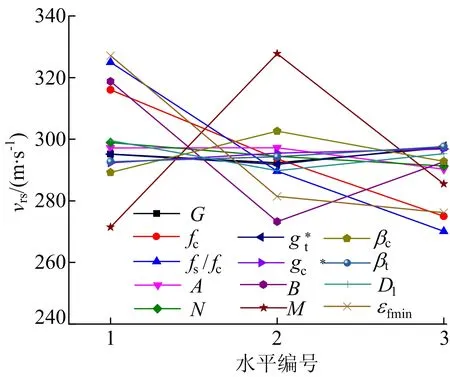
图8 各因素指标效应曲线
5 结 论
本文使用RHT本构模型和SPH-Lagrange耦合方法对混凝土侵彻试验进行模拟,对不同卵形弹丸形状系数下混凝土侵彻过程进行数值分析,并分析RHT本构模型参数的敏感性,得出以下结论:
(1) RHT本构模型和SPH-Lagrange耦合方法适用于大变形的混凝土侵彻模拟,并能够很好地表征混凝土在冲击作用下的压剪及拉伸破坏行为。
(2) 随着弹丸形状系数增加,混凝土非贯穿试验中侵彻深度、损伤范围增加;贯穿试验中子弹剩余速度与弹丸形状系数成正相关,而混凝土动力响应与之成负相关。
(3) RHT本构模型参数中敏感性较高的为fc、fs/fc、B、M和εfmin,相对不敏感的参数为G、A、N、gt*、gc*、βc、βt和D1,在标定参数时根据其敏感性强弱进行分类,可更准确地确定模型参数。
