基于时空多维的VMD-GAT-Attention短时交通流量组合预测模型

田帅帅, 殷礼胜, 何怡刚

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

近年来,智能交通领域的建设日益凸显,交通规划和交通诱导成为智能交通领域的研究热点,而准确的交通流量预测更是交通规划和诱导的前提,其中,短时交通流量预测精度逐渐被作为交通领域的关键性问题[1-3]。面对复杂交通环境的预测精度要求不断提高,使用单一模型难以应对具有时空特性、非线性等多特性的短时交通流量预测,学者们针对此交通领域,研究了众多的组合模型。文献[4]通过使用图卷积网络和门控递归单元相结合的组合模型方法,同时捕获交通流量的时空特征,但忽略了交通流量序列的非线性特点,难以预测剧烈变化的交通流量;文献[5]使用变分模态分解(variational mode decomposition,VMD)算法处理非线性、非平稳交通领域的客流量数据,并通过构建的神经网络进行组合模型的预测,但是并未对VMD算法的分解参数进行分析,容易造成数据分解不够充分,同时忽略了预测节点周边的空间特性;文献[6]利用集成经验模态分解算法将原始序列分解为多个模态,再使用双向长短期记忆神经网络和注意力机制进行交通流量的预测,细化交通流量预测的需求,提取交通流量的时间特征,同样并未考虑到预测交通节点的空间特征,没有更进一步探索交通流量中时间与空间的内在依赖性。

从交通流量序列的时空依赖性、非线性的内在规律角度来看,以上研究忽略了交通流量中的时空依赖性的内在规律或者序列的非线性、非平稳性特点,没有充分挖掘交通流量的内在规律,各有其缺点。综上所述,本文提出一种基于改进粒子群优化的VMD、结合图注意力网络(graph attention networks,GAT)与注意力机制相结合的组合预测模型。首先,在时间维度上,利用改进粒子群算法(improved particle swarm optimization,IPSO)优化VMD,将非线性的交通流量时间序列分解为不同频率的相对平稳的时间序列信号,确保VMD算法能够充分而有效地挖掘交通流量时间序列的信息;利用分解后的每组序列与原始序列的相关性系数,构建有效的分解模态;其次,在空间维度上,针对有效的分解模态的相关性系数来构建不同的GAT,提取相对稳定的交通流量数据中的空间特征;同时,利用注意力机制共同构建深度学习模型,以提取时空信息,通过计算每个时空特征注意力权重,使交通流量预测的精度进一步得到提升;最后,使用PeMS现实数据集进行交通预测模型的搭建,并与子模型GAT模型、VMD-GAT模型、VMD-GAT-Attention和PSO-VMD-GAT-Attention,以及长短期记忆网络(long short-term memory,LSTM)、差分自回归移动平均模型(autoregressive integrated moving averaga model,ARIMA)等多个模型的拟合效果以及预测精度进行对比,以验证组合预测模型的可行性和优越性。

1 交通流量预测组合模型相关理论

1.1 交通流量预测问题的形式化描述

交通路网中的短时交通流量具有非线性、时空依赖性特点,其中,路网中的节点更是具有典型的空间拓扑关系。交通路网中车流量通过预测节点的变迁示意图如图1所示,其中,{1,2,…,n}为预测节点,箭头的指向表示道路车辆行驶方向,由此车辆行驶过程中通过预测道路节点,使相邻道路节点共同组成动态交通路网,路网上车流量的变化构成了相应的时空交通流量,即Q(t)=(q1[t-Δt,t],…,q1[t-mΔt,t-(m-1)Δt],q2[t-Δt,t],…,q2[t-mΔt,t-(m-1)Δt],…,qn[t-Δt,t],…,qn[t-mΔt,t-(m-1)Δt])。其中:Δt为交通流量采样时间间隔;n为交通路网连接节点个数;m为时间间隔个数。本文通过以上时空数据Q(t),预测交通路网未来n个节点交通流量(q1[t,t+Δt],q2[t,t+Δt],…,qn[t,t+Δt])。

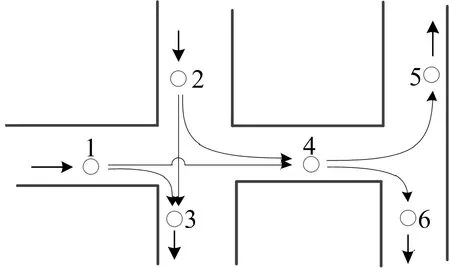
图1 交通路网中车流量通过预测节点的变迁示意图

为了有针对性地解决交通预测问题，首先利用IPSO优化VMD算法,将交通流量分解为相对平稳的交通流量信号;然后利用GAT提取平稳交通信号下的路网空间特征;最后利用注意力机制将各个模态提取到的空间特征节点进行融合,进而提高模型预测精度。

1.2 粒子群算法的改进

粒子群算法(particle swarm optimization,PSO)属于一种仿生算法,具有收敛速度快,所需调整参数少的特点[7],但PSO有易陷入局部最优解以及收敛速度慢的缺点,本文提出改进粒子群算法IPSO。

(1) 算法在搜寻过程中,粒子速度的权重系数w一般为常数,易陷入局部最优值。因此为动态地调整搜寻空间,以保证更有效地收敛到全局最优解，设置自适应权重,即

w=

(1)

其中:wmax、wmin分别为初始惯性权重的最大值和最小值;f(xj)为当前迭代中的第xj个粒子的适应度值;fave、fmin分别为当前所有粒子适应度的平均值和最小值。

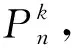
(2)

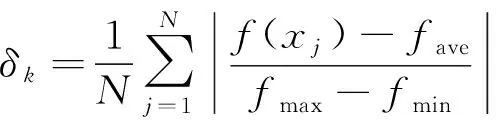
(3)

(4)

其中:N为粒子的个数;fbest为当前全局最优粒子对应的适应度;fmax为当前粒子群中最大适应度值;s为2～4的随机数。

利用变异结果与当前迭代中全局最优位置结合的变异方法,保证粒子变异优异性。

(5)

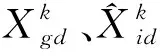
1.3 VMD算法

VMD是一种自适应、非递归的新型提取信号特征的方法[8]。本质上属于维纳滤波,在处理含有噪声的信号中具有更好的鲁棒性,VMD算法详细分解推导过程参见文献[9]。

通过VMD算法将交通流量时间序列Q(t)分解为K个平稳的交通流量模态分量。核心求解是通过约束条件,即分解的K个交通流量模态之和等于原交通流量,不断迭代更新交通流量分解模态的中心频率wk和带宽,由此分解得到K个本征模态函数(intrinsic mode function,IMF)。

(1) 将交通流量Q(t)模态分解的约束性变分问题转化为非约束性变分问题。引入拉格朗日乘法算子λ(t)和二次惩罚因子α,以求解交通流量序列分解的最优解。其中,非约束性变分问题模型为:

L({Qk(t)},{wk},λ(t))=

(6)

其中:Qk(t)为第k个交通流量分解模态;∂t为对t求偏导;δ(t)为狄克拉函数;*为卷积运算符。

(2) 采用乘法算子交替法,以不断搜寻增广拉格朗日函数鞍点的方式,迭代得出交通流量分解模态Qk(t)、wk及λ(t),寻找交通流量分解的最优交通流量分解模态集合。

(3) 在频域范围内,利用在范数下的傅里叶等距变换求解交通流量分解的变分问题，即

(7)

(8)

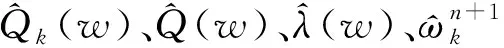
VMD算法的求解实际上是将分解的K个交通流量模态在频域中求解,然后利用傅里叶变换到时域,得到分解模态{Q1(t),Q2(t),…,Qk(t)}。

1.4 交通路网下的GAT

GAT是在图卷积网络的基础上引入注意力机制,对图结构中每个节点的临近节点进行特征线性变换与加权求和[10]。核心思想是通过关注每个图节点的邻接节点特征来更新每个节点的特征向量的表示,隐式地为一个邻域内的不同节点指定不同的权重。

在交通路网当中,预测节点在实际空间中相互连接,构成了相应的图结构。将图1交通路网转化为有向图结构,如图2所示。路网中预测节点用图节点表示,车辆在道路上沿节点行驶的路线用有向边表示。

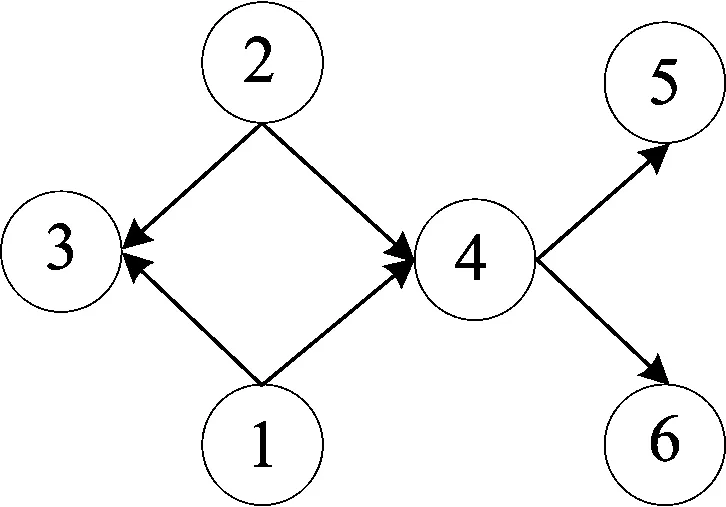
图2 交通路网转换的图结构

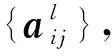
(9)

(10)

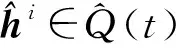
1.5 注意力机制

注意力机制应用场合广泛,在自然语言处理领域与交通领域效果十分显著[11-12]。核心思想是从大量信息中有选择地筛选出重要信息,计算不同信息的权重系数。

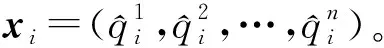
图3 注意力机制模型结构

2 短时交通流量组合预测模型构建

为解决短时交通流量非线性、时空依赖性,构建针对性的IPSO-VMD-GAT-Attention组合模型挖掘深层特征,总体框架如图4所示。

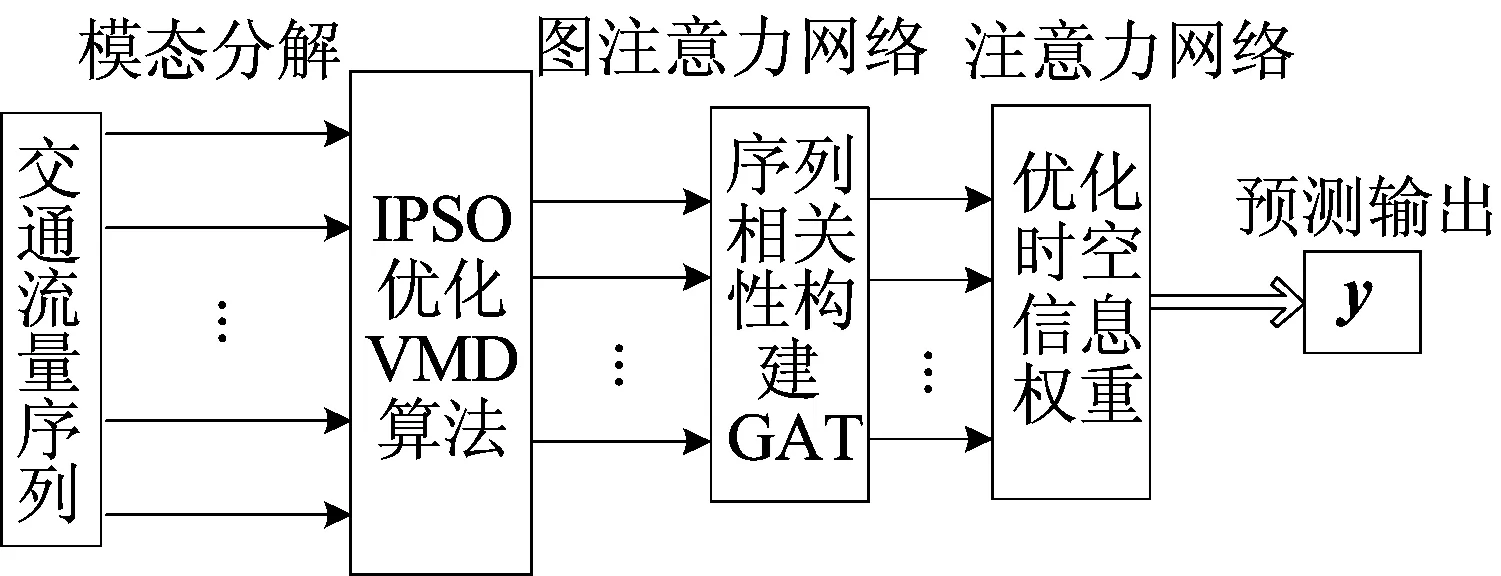
图4 IPSO-VMD-GAT-Attention组合模型总体框架

VMD算法作为一种改进模态分解算法,在频域上能自适应分解出相对平稳的时序模态;同时,使用IPSO优化VMD算法选取适当参数,保证交通流量的充分分解;其次使用图注意力网络提取空间特征信息,以及注意力机制聚焦主要信息权重和降低次要信息权重。

2.1 短时交通流量分解的IPSO-VMD算法

VMD算法能分解出相对平稳的模态分量,但VMD算法分解结果又受到分解模态个数K和二次惩罚项系数α的影响[13-14]。改进粒子群算法优化的变分模态分解(IPSO-VMD)算法结构如图5所示,对此,使用IPSO-VMD算法结构进行组合参数寻优。

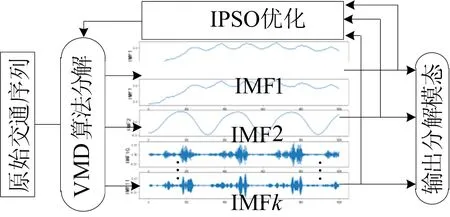
图5 IPSO-VMD算法结构

IPSO-VMD算法分解交通流量步骤如下:

(1) 选取1.1节构建的交通流量数据Q(t)为VMD分解的序列,作为算法输入数据。

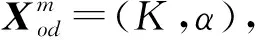
(11)

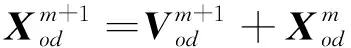
(12)

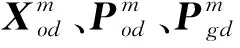
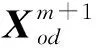
(5) 利用步骤(4)产生的(K,α)粒子信息,使用VMD算法的分解,得到K个相对平稳的交通流量子序列{Q1(t),Q2(t),…,Qk(t)}。

(6) 对VMD算法分解后的K个交通流量分解模态,计算对应的包略熵[14],即

(13)

其中:Qj为分解后的第i个交通流量分解模态;pj为Qj归一化数据;Ej为分解模态Qj对应的包略熵,即Qj对应的适应度值,以此更新全局最优值与个体局部最优值。

(7) 若尚未达到最大迭代次数或仍有下降趋势,返回步骤(3)继续执行,否则利用全局最优粒子信息(K,α),通过VMD算法分解输出K个交通流量模态分量。

2.2 基于相关性改进的深度学习模型

通过VMD算法分解后的相对平稳交通流量模态,是包含有噪声的分解模态。而利用相关性系数可有效分析分解模态与原交通流量的相关性,进而选择有效分解模态;同时,采用不同GAT来提取不同的相对平稳时间序列的空间特征;但是,由于不同的分解模态包含信息量是不同的,若提取特征维度数设置不当,会影响模型体积的增大以及预测精度,导致训练困难。本文采用有效分解模态的相关性系数,确定GAT的输出维度,以针对不同分解模态构建基于短时交通流量的深度学习模型。

2.2.1 利用相关性改进的深度学习模型

通过上述有关模型相关性的分析,本文将相关性系数应用于如下2个方面:① 利用分解模态与原交通流量相关性系数大于0.1的条件,筛选出有效的分解模态;② 使用有效分解模态对应的相关性系数搭建各自的GAT。

计算交通流量分解模态{Q1(t),…,Qi(t),…,Qk(t)}与原交通流量Q(t)的相关性系数ρ(Q(t),Qi(t)),即

(14)

其中:x、y分别为原交通流量与交通流量分解模态序列;ρ(x,y)为序列x与y的相关性系数;E(x)为序列x的数学期望[15]。

通过计算得到的K个交通流量分解模态与原交通流量两者相关性系数{ρ1,ρ2,…,ρk},选择相关性系数大于0.1的v个分解模态{Q1(t),Q2(t),…,Qv(t)}作为有效分解模态。

利用有效分解模态的相关性系数{ρ1,ρ2,…,ρv}来确定GAT的特征输出维度，即以最小相关性系数ρmin作为基值,计算相应GAT的特征输出维度,计算公式为:

(15)

其中:计算得到的ρ0为原交通流量的自相关系数;Ni为第i个交通流量模态分量对应GAT的特征输出维度;ρi为第i个交通流量模态分量与原交通流量序列的相关性系数。

为构建深度学习的总体结构框架,利用相关性改进的深度学习模型如图6所示,框架中对VMD算法分解的有效模态分量分别构建不同的GAT,挖掘了平稳交通流量的空间信息;其次引入注意力机制对GAT输出的空间特征赋予不同的权重系数,加强了对主次信息的提取与辨别能力,从而实现交通流量的预测。

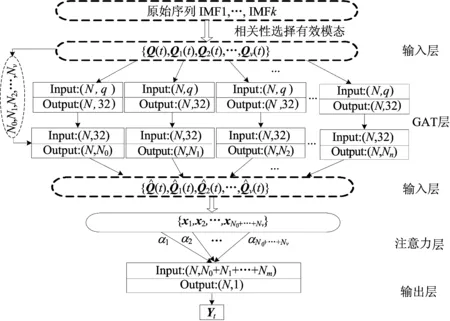
图6 利用相关性改进的深度学习模型

2.2.2 基于短时交通流量的深度学习模型

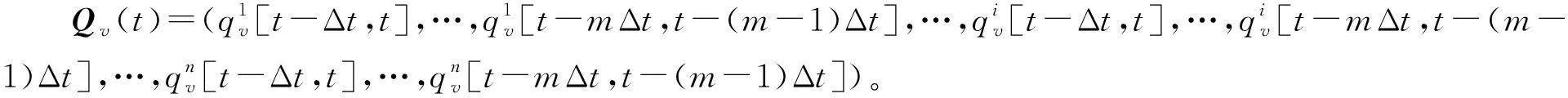
(16)

(2) GAT层。 对分解后的相对平稳时间序列与原交通序列进行空间特征的提取。

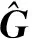
(17)

(18)

(3) 注意力层。以时间的角度,提高主要空间特征xi的权重,降低次要空间特征权重。由(19)～(21)式针对不同的空间特征计算得出注意力权重系数αi和输出矩阵Pt,即

σi=tanh(waxi+ba)

(19)

(20)

(21)

其中:σi为xi与Pt的关联程度;wa为注意力层连接权重矩阵;αi为注意力权重系数;softmax函数为对σi进行归一化处理。

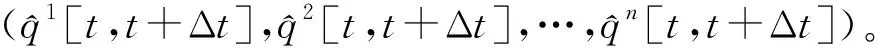
Yt=σl(wlPt+bl)

(22)

其中:σl为激活函数;wl为权重矩阵;bl为偏置。

(5) 损失函数与优化算法。本文深度学习模型选择均方误差(mean square error,MSE)函数作为优化目标,其中目标函数计算公式为:

(23)

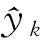
对于优化算法,选择Adam算法更新模型中的偏置与权值,采用mini-batch进行训练,batch-size设置为64,学习步长初始设置为0.001,从第30个epoch开始,每隔10个epoch学习率衰减为原来的1/5,dropout设置为0.4。

2.3 基于交通流量的组合预测算法

本文为解析交通流量的时空依赖性、非线性的特征,针对性地提出了短时交通流量IPSO-VMD-GAT-Attention组合预测模型,模型框架如图7所示。

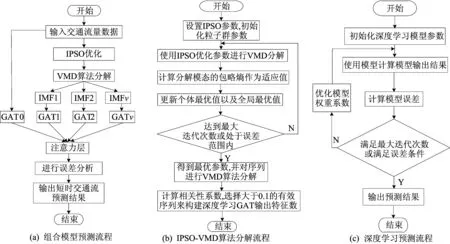
图7 短时交通流量的IPSO-VMD-GAT-Attention组合预测流程图

具体步骤如下。

(1) 将实际预测路网按照1.1节道路节点进行连接,构成时空数据Q(t)作为VMD算法输入数据。

(2) 使用IPSO算法搜寻VMD最优参数,然后分解时空数据Q(t)得到k个IMF序列。

(3) 分别计算分解模态的相关性系数,将相关性系数大于0.1的模态作为有效模态,并计算对应GAT特征输出维度数,构建的相关性与GAT特征维度见表1所列。

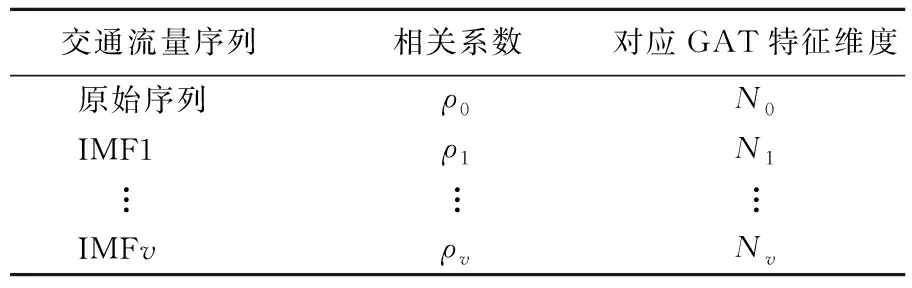
表1 交通序列间的相关性系数及GAT特征维度

(4) 利用相关性系数构建GAT,并与注意力机制搭建如图6所示的深度学习模型。将步骤(3)提取的有效模态分量与原始数据作为深度学习模型的输入数据,并进行训练,设置参数。

(5) 训练组合模型。判断误差是否处于最大误差范围内且一定范围内没有变化,以及是否在最大迭代范围内利用训练好的模型进行预测。

3 工程应用

3.1 短时交通流量数据选取

实验数据取自于加州高速路网PeMS交通流量数据集,交通数据集采集点分布地图如图8所示。交通数据采集自2018年1月1日至2月14日之间共31个交通节点且间隔为5 min的数据信息。将前36 d数据作为训练数据,其余作为测试数据,同时使用前6个时刻交通流预测下一时刻的交通流。

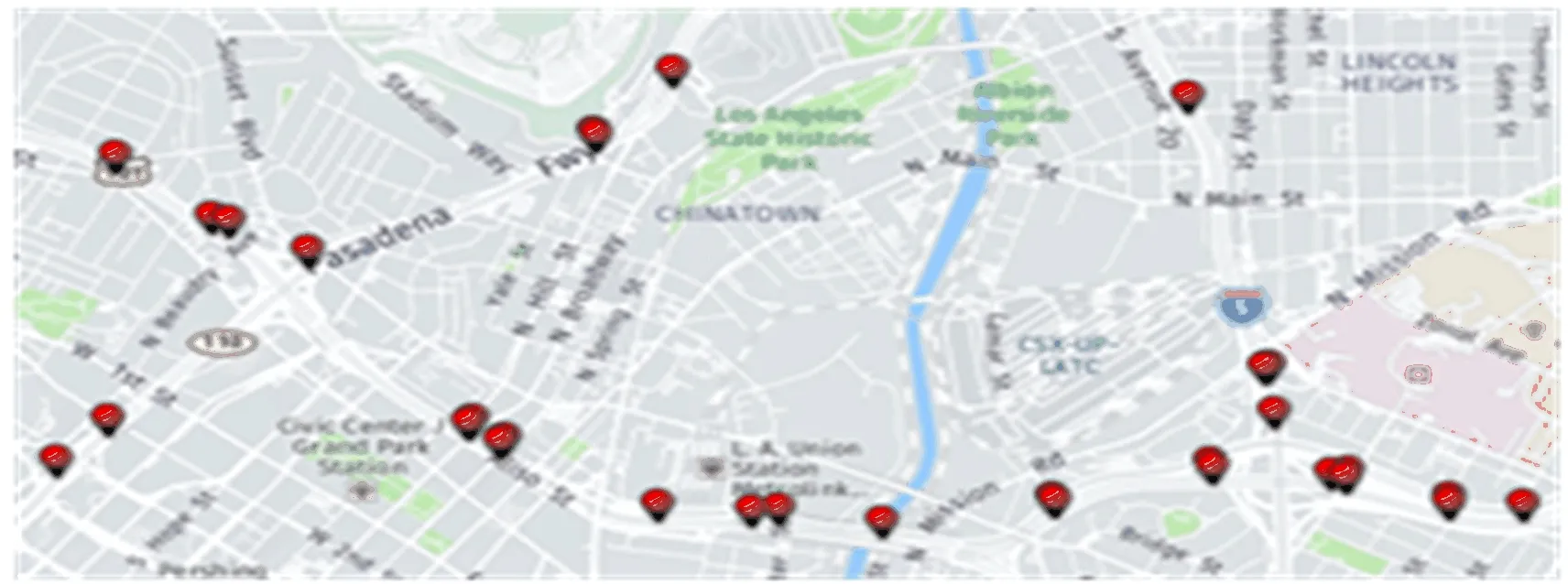
图8 交通数据集采集分布点

采用线性函数归一化原始数据,归一化后的部分交通流量原始数据如图9所示,图9中，横轴为每5 min采样得到的数据。由图9可知，交通流量在大趋势上是一致的,但是具体到细微之处,是完全不一样的,需深层次挖掘交通流量特征。

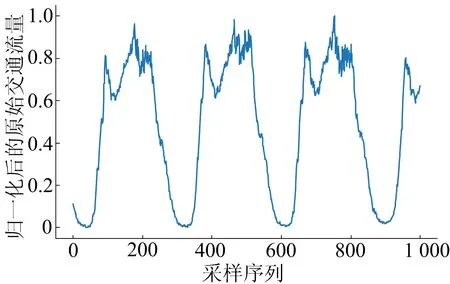
图9 部分原始交通流量数据曲线

3.2 基于PeMS数据组合预测模型应用实现

利用IPSO算法搜寻VMD算法最优分解参数,IPSO和PSO寻优迭代曲线如图10所示。

图10 IPSO和PSO迭代曲线

由图10可知,IPSO-VMD算法寻优能力更好且收敛速度快,而PSO-VMD算法陷入局部最优解中。最终得到的最优参数组合为(1 324,9),输出IMF1～IMF9共9个分解模态。计算相关性系数大于0.1,得到IMF1～IMF5有效分解模态,有效模态的部分序列如图11所示。

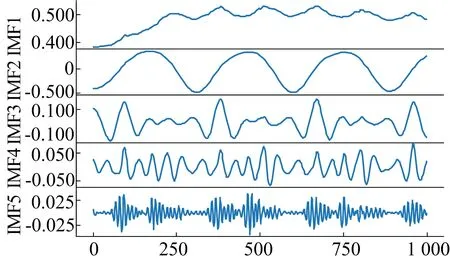
分解后采样序列图11 有效模态的部分序列图

计算有效模态与原交通流量的相关性系数及GAT特征输出维度数，见表2所列。

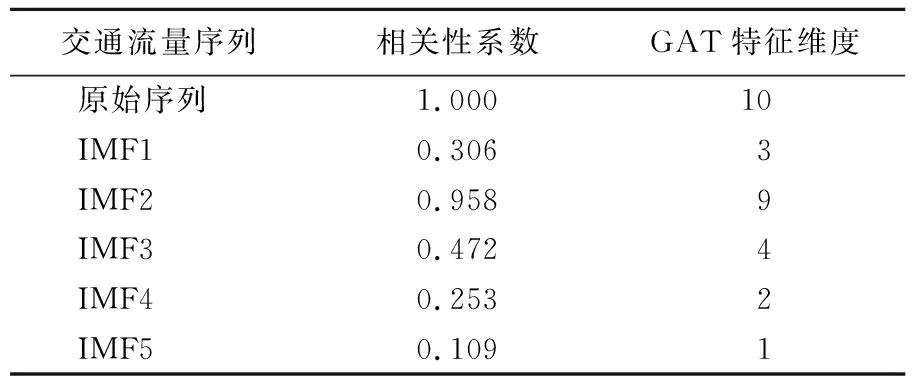
表2 相关性系数及GAT特征维度数

在实际中GAT注意力的个数在不同深度学习任务中选取是不同的。通过实验得到注意力个数与预测误差如图12所示,由图12可知,注意力个数为3时是合适的。

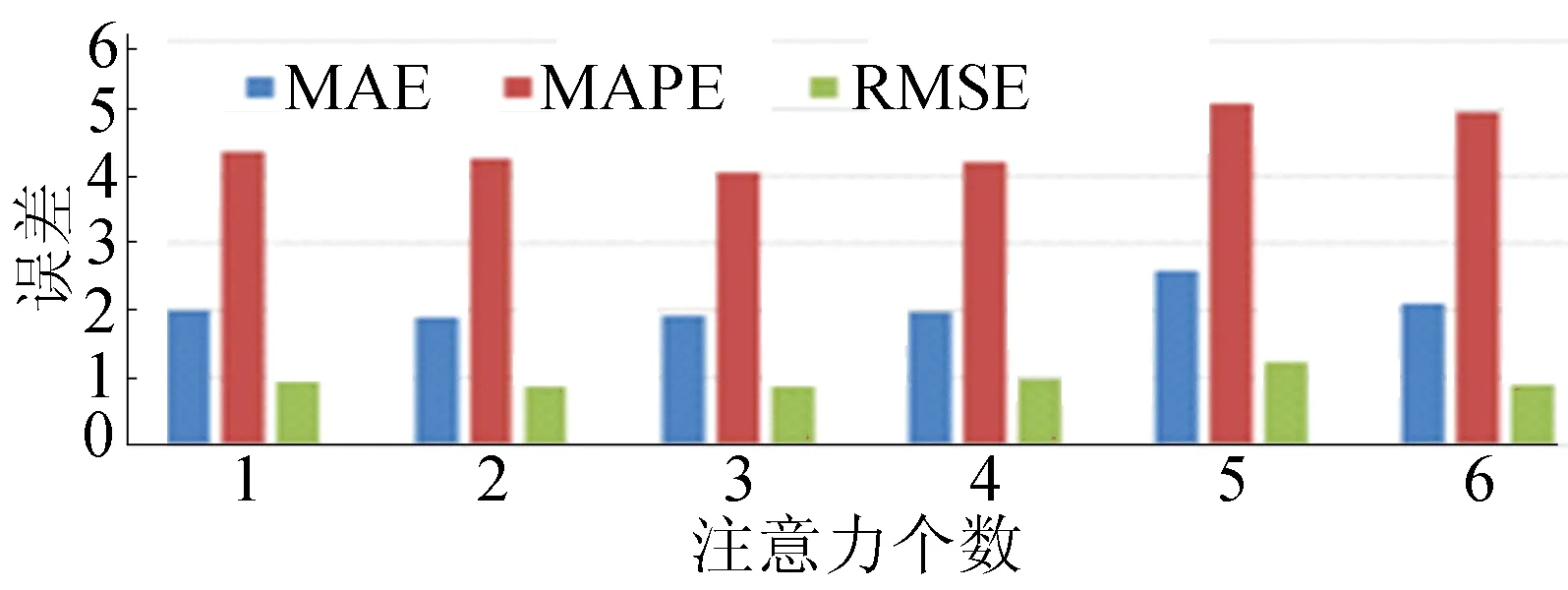
图12 不同注意力数下的误差柱状图

构建图6结构模型进行预测,交通路网下的交通流量拟合图如图13所示。

图13中交通流量的单位为每5 min通过的车辆总数。由图13a可知,各交通节点预测值与真实值的拟合曲线比较接近;由图13b可知,单节点交通流量总体上十分接近,即使在变化剧烈的12:30—13:00时刻也有较好的拟合效果。

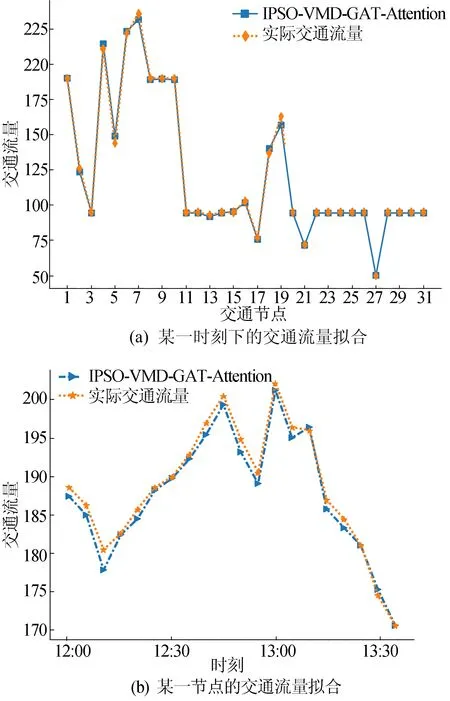
图13 交通路网下的交通流量拟合

3.3 实验结果分析

为更全面评价模型的有效性与优越性,选择预测值与原始值的平均绝对误差EMA、均方根误差ERMS和平均百分比误差EMAP评价模型。

(25)

(26)

(27)

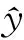
不同交通流预测方法的误差对比见表3所列,预测结果与实际值在某一节点的变化拟合图和某一时刻所有节点的拟合图如图14所示。

由表3可知,本文提出的预测模型与未考虑空间特征的时间序列模型LSTM深度学习网络以及ARIMA算法相比,预测误差都低,说明从空间维度考虑交通路网问题是有效的,能够提高预测精度;同时,本文从时间维度将VMD算法进行交通流量时间序列分解,使非线性交通流量序列得以转为平稳序列;而且IPSO算法能够更快地寻找到全局最优值,同时注意力机制的应用提高模型对交通特征的分析能力,也进一步提升了预测精度。

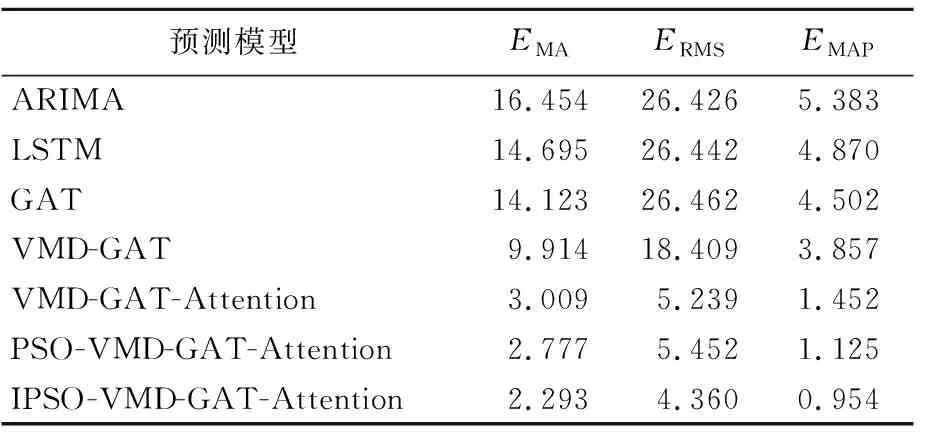
表3 不同交通流预测模型误差对比

由图14a可知,在12:30—13:00之间交通流量剧烈变化的时间段内,只考虑时间特性的LSTM与ARIMA模型与只考虑空间特性的GAT模型相比,也说明了从空间角度分析交通流量效果比从时间角度分析较好。

图14 多个模型下交通路网下交通流量拟合对比

同时,观察VMD-GAT时空交通流量拟合效果有些偏差,说明简单地从时空角度分析,预测效果一般,而具有时空特征且进一步使用注意力机制模型的VMD-GAT-Attention与PSO-VMD-GAT-Attention模型,却有很好的交通流量预测精度;同时,使用IPSO算法优化的IPSO-VMD-GAT-Attention模型拟合效果又有所改善。由图14b可知,对于IPSO-VMD-GAT-Attention模型拟合效果最好,且该模型在交通路网上的所有预测节点有更高的拟合,而其余预测模型在不同预测点有较大的差别、预测精度不一。由此可知,IPSO-VMD-GAT-Attention组合预测模型不仅在总体上提高了短时交通流量的预测精度,而且各个预测点的值与实际值拟合程度较高。

4 结 论

根据交通流量的时空依赖性、非线性特点,本文提出了一种基于IPSO优化的VMD算法,并与GAT以及注意力相结合的组合预测模型。通过仿真对比结果可知,在交通流量预测精度方面,使用GAT提取空间特性与LSTM、ARIMA等时间序列预测模型相比,从空间角度分析交通流量,对于预测精度有较大提升;同时,使用VMD算法将非线性交通流量序列转化为平稳时间序列是有效的;对于提取的交通流量时空特征,不能简单地组合,应灵活地运用注意力机制,将时空特征很好地融合在一起,在一定程度上能提高短时交通流量的预测精度。但是,本模型没有考虑假期、天气、事故等对交通流量的影响,即没有考虑更高维度的影响,此类问题将是下一步的研究方向。