基于Fly-back变压器模块化均衡方法

刘征宇, 尤 勇, 朱诚诚, 姚利阳

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230009)

0 引 言

锂离子电池因高能量密度、高电压、循环寿命长、低放电率和无记忆效应等优越的性能在电动汽车领域得到广泛应用[1]。实际应用中,需要很多锂离子电池串并联驱动电动汽车,而随着电池包反复充放电次数增多,电池组的不一致性不断扩大，导致各单体电池截止电压差增大。当电池组中任一单体电池电压达到充放电截止电压时就必须停止充放电,因此大部分单体电池能量均不能充分利用[2-3]。在安全的前提下,设计电池组均衡电路是提升电池组容量利用率的有效途径。

过去的十几年中,电池组均衡器已经有了长足的发展,但仍有很多不足。例如:电阻分流器[4]结构简单,但是能量利用率非常低;开关电容器[5]均衡速度快,但是开关的电压应力大、易损坏;降压升压转换器[6-7]均衡效率较高且易扩展,但控制难度高且均衡时间长;反激转换器[8]能实现电气隔离，均衡控制简单,但是成本高;正激-反激转换器[9-10]均衡效率高且变压器磁化率低,但是均衡精度低。其中基于变压器的均衡方案具有易于隔离、效率高、控制简单等固有优点。

利用多绕组变压器作为均衡器的均衡方法,是将一组单体电池通过单个多绕组变压器正向耦合,在此电池组中任意单体之间能够交换能量,并且能量利用率高。文献[11]提出了一种使用基于正向转换的多绕组变压器的均衡器,这种拓扑电路的最大优点是通过脉冲宽度调制(pulse width modulation,PWM)信号驱动金属-氧化物半导体场效应晶体管(metal-oxide-semiconductor field-effect transistor,MOSFET),可以将能量从任何较高电压的电池直接传输到较低电压的电池;但当电池组是由数百个单体电池串联连接的长电池串时,变压器会产生体积大、复杂性高以及难实现的问题。上述问题可以通过模块化来解决。文献[12-13]提出了一种将Fly-back变压器进行模块化的方法,实现模块内与模块间同时进行均衡,能够解决实际应用问题。另外采用多绕组变压器作为均衡器时,由于客观原因,变压器磁芯上各绕组有效匝数比不均匀的问题会影响最终均衡结果。为了解决此问题,文献[14]提出增添通用滤波器进行调整,根据设置适当的滤波器参数和开关频率,减小绕组匝数不同带来的影响。但是文献[12-13]的方法在均衡后精度还有一定的提升空间,文献[14]的均衡方法不能实现模块化均衡。因此,以Fly-back变压器为基础的均衡器多数不能实现模块化设计，并且均衡器体积庞大,均衡精度低,不易于实际使用。

本文提出一种改进的变压器作为均衡器,不仅可以实现模块化均衡,还能有效提升均衡精度,减小均衡器体积,有利于实际应用。

1 均衡拓扑结构

本文提出的基于多绕组反激式变压器的模块化均衡电路整体均衡结构如图1所示。整个模块化均衡结构中n个串联的电池被分成x个模块,每个模块中有y个单体电池、1个多输入单输出变压器、y个MOSFET开关、y个电容、y个电感。

图1 基于多绕组Fly-back变压器模块化拓扑图

本文提出的均衡方案由初级侧电路和次级侧电路2个部分组成。初级测电路包括每一个模块的初级侧,并通过相同的电路与电池相连。对于利用多输入绕组变压器的正向功能实现模块内y个电池电压均衡。为表示与图1中非特定模块相关,选取第m(m=1,2,…,x)个模块,电路结构如图2所示。每一个模块内均包含y个相同的电路结构,且y个绕组并联缠绕在磁芯Tm上。能量间接地从较高电压电池转移到较低电压电池,实现模块内电池电压均衡。次级侧电路包括所有模块的次级侧,并且所有模块次级侧并联,因此可以利用变压器的反向功能实现电压均衡。利用反向变压器来实现模块之间能量传递,进而达成电池串所有电池的电压均衡,并且无需去磁电路即可实现变压器的去磁。

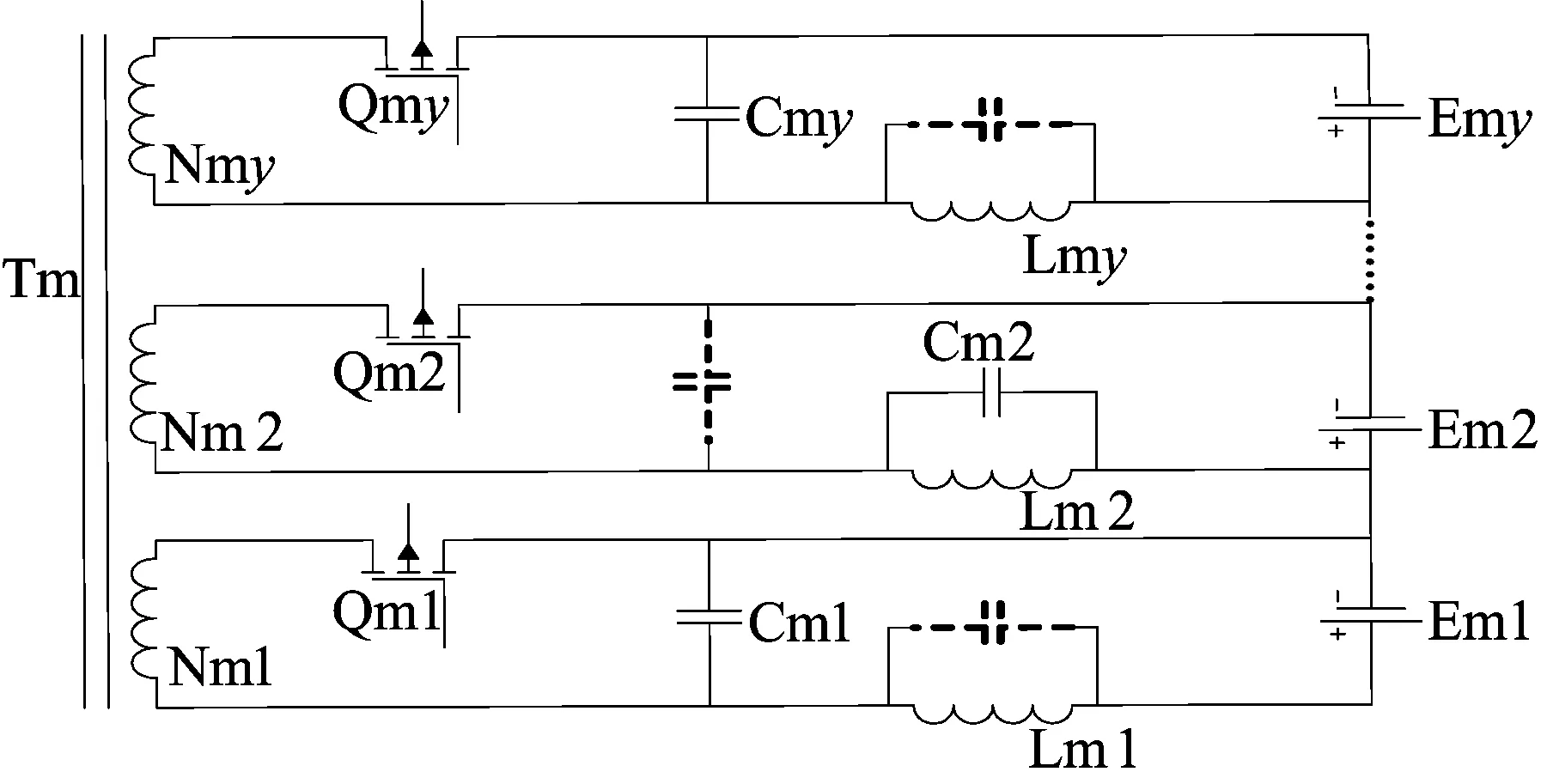
图2 模块内电池电压均衡图

本文主要创新点是根据每个单体电池的单元电路设计均衡拓扑,并配合均衡策略降低多绕组变压器自身绕组匝数比不均匀对最终均衡结果产生的不利影响,从而提升均衡精度,降低各单体电池之间的电压差。以电池Em1为例的单元电路,Nm1是多绕组变压器的一个初级侧绕组,在电池单元Em1和绕组Nm1之间插入开关装置Qm1,通常是MOSFET。并且所有的MOSFET仅由隔离的PWM驱动。对于第m个模块而言,Nm1、Nm2……等N个初级侧绕组匝数比不均匀,设计单元电路中电感 L11、电容C11与电池E11串联形成滤波电路,并设计以一对互补的变频PWM信号(PWM+,PWM-)为基础的均衡策略,降低单元电路中绕组匝数不均匀带来的不利影响。

2 均衡过程

2.1 模块化均衡整体流程

本文提出利用多绕组变压器构成模块化自动同步均衡器,通过变压器正向功能实现每个模块内单体电池电压均衡,反向功能实现模块之间电压均衡。通过一对互补的PWM信号分别控制偶数模块和奇数模块的MOSFETS开关,实现电池电压自动均衡,并且无需变压器去磁电路。为了简化模块均衡的分析,选择具有8个单体电池的串联电池组,并通过模块化将其分成M1、M2 2个模块,每个模块包括4个电池,如图3所示。

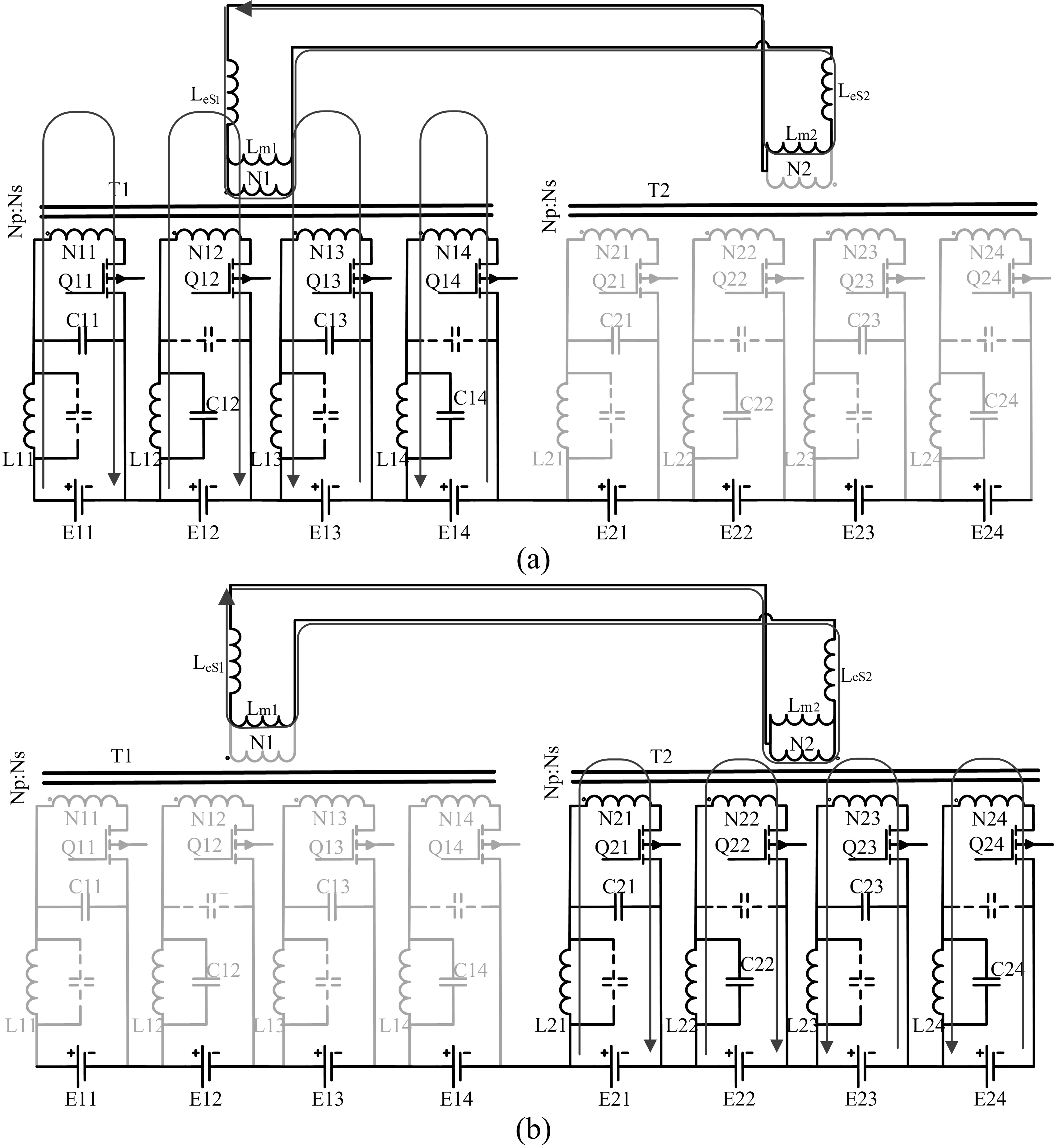
图3 均衡操作模式

单体电池的初始电压满足:

VE21>VE11>VE22>VE12>

VE23>VE13>VE24>VE14

(1)

显然,M2的电压(VM2=VE21+VE22+VE23+VE24)比M1的电压(VM1=VE11+VE12+VE13+VE14)高。流进电池正极的电流为正向,其他为负向;对于变压器次级绕组,电流逆时针为正向,其他为负向。若要通过滤波器消除转换器绕组匝数不均匀现象,则需假定转换器所有初级绕组匝数相同,并且转换器有相同的参数,包括磁化电感、漏电感。模块内绕组电阻忽略不计。

2.2 模块化均衡阶段

稳定状态下,一个开关周期内有2个操作模式,即模式Ⅰ和模式Ⅱ,其理论波形图如图4所示。

图4 均衡波形

(1) 模式Ⅰ,即模块化均衡第一阶段(t0-t1)。t0时刻,M2的控制开关Q21～Q24断开,同时M1的所有开关Q11～Q14接通。

M2初级侧的均衡电流在t0时刻变为0,同时次级侧感应电流也截止。M1初级侧的各单体电池基于转换器的正向功能,其模块间均衡电流可实现自动流动,见图3a。已知初始电压VE11>VE12>VE13>VE14,假设iE11、iE12负向流动,iE13、iE14正向流动,且满足|iE11|>|iE12|、|iE14|>|iE13|。所有初级绕组具有相同的匝数,根据法拉第定律,M1内任一初级绕组电压VP1k(k=1,2，…，4,下同)与初级绕组平均电压VP1v相等。

此时,模块Ⅰ内初级绕组电压VP1k可以表示为:

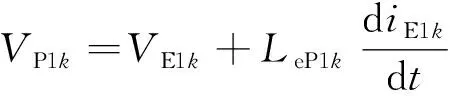
(2)

并得出均衡电流iE1k(t)的表达式为:

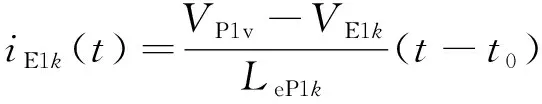
(3)

其中:VE1k、iE1k分别为M1中E1k的单元电压和均衡电流;LeP1k为M1中第k个初级绕组的漏电感。

VP1k和VE1k之间的电压差施加到漏电感LeP1k上,均衡电流iE1k从0线性上升,如图4所示。

模块中转换器的初级侧和次级侧绕组匝数分别为NP、NS,且匝数比n为NS/NP。模式Ⅰ的次级侧电压环路方程为:

(4)

模块Ⅰ和模块Ⅱ中转换器的初级绕组与次级绕组电压关系方程分别为:

(5)

(6)

其中:iTS为次级均衡电流;LeS1、LeS2和VS1、VS2分别为变压器Ⅰ、变压器Ⅱ次级绕组漏电感和电压;VP2k、VP2v分别为M2内任一初级绕组电压和初级绕组平均电压。

在t0时刻,次级均衡电流iTS(t)的方向由负向瞬间变为正向,使M2变压器消去磁芯能量。求解(4)式可以得出iTS(t)表达式为:

(7)

由于VP2v>VP1v,iTS(t)会以一固定斜率递减。根据(5)式、(6)式推导出M2初级侧绕组电压表达式为:

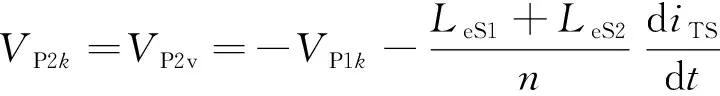
(8)

在上一周期存储在电感Lm1和Lm2的能量基于反向转换被传送到M1中的单元,实现了2个模块之间的均衡。

M1的次级电压反向作用于电感Lm1,磁化电流iLm1(t)以一固定斜率递减,即

(9)

iLm1(t)减至0之后,以相同斜率负向增加,直至t1时M1结束。当控制开关Q11～Q14关断后,此反向电流能为M1中变压器退磁提供前提条件。

M2的磁化电流iLm2(t)等于次级均衡电流iTS(t),因此M1内2个电流波形图完全一致。

(2) 模式Ⅱ,即模块化均衡第二阶段(t1-t2)。t1时刻,M1的控制开关Q11～Q14断开,同时M2所有开关Q21～Q24接通。M1初级侧的均衡电流在t0时刻变为0,同时次级侧感应电流也截止,见图3b。

此时,模块Ⅰ内初级绕组电压VP2k的表达式为:

(10)

并得出均衡电流iE2k(t)的表达式为:

(11)

VP2k和VE2k之间的电压差施加到漏电感LeP2k上,均衡电流iE2k从0线性负向增加,如图4所示。

在t1时刻,由于iLm1连续流动,迫使次级电流iTS(t)瞬间上升,使M1变压器磁芯复位而不使用任何额外的去磁电路。同样求解(4)式可以得出iTS(t)的表达式为:

(12)

由于VP2v>VP1v,iTS(t)会以一固定斜率递减。根据(5)式、(6)式推出模块Ⅰ的初级侧绕组电压表达式为:

(13)

t1时刻iLm2(t1)=0,M2的次级电压反向作用于电感Lm2,磁化电流iLm2(t)以一固定斜率递增,即

(14)

iTS(t)减至0之后,以相同斜率反向递增,直至t2,模式Ⅱ结束。

从iTS(t)=0开始,通过电流iLm1和iLm2,M2中的能量逐渐存储在磁化电感Lm1和Lm2中。这为控制开关Q21～Q24关断后2个模块之间的均衡提供了前提条件,并且无需额外的均衡电路。由原理图3b可知,iLm1(t)与iTS(t)在模式Ⅱ均衡过程中大小相同、方向相反,因此波形图完全相反。

2.3 单元均衡过程

事实上,变压器制造时由于工艺上的原因总会造成绕组匝数比的不均匀。变压器作为本文中设计均衡器的核心元器件,降低变压器均衡时带来的误差是本文的主要工作之一。为了补偿多绕组变压器中的非均匀匝数比,设计一种通用滤波器配合开关频率进行微控制多绕组变压器的均衡电压,降低系统本身带来的误差。模块内电池电压均衡时,这些不均匀的绕组匝数产生的不相等二次电压会干扰均衡结果,导致最终模块内电池电压差值偏大。本文采用通用滤波器来解决上述问题。

电路中第k个通用滤波电路结构如图5所示。通用滤波器可以通过去除电容C1k作为频带放大CL滤波器,解决二次电压偏低的问题,也可以通过去除电容C0k作为频带衰减LC滤波器,解决二次电压偏高的问题,从而实现模块内电池电压更好的均衡。

图5 通用滤波器结构

对任一个绕组，仅会出现上述情况的一种。若某一绕组数偏多,则会产生偏高的正向输出电压。对于这种情况,通用滤波器当作频带放大功能,其传递函数经拉普拉斯变换后为:

A=L0kL1kC0kC2k,

B=L0kC0k+L0kC2k+L1kC2k

(15)

其中:下标k表示拓扑结构中第k个电池的均衡电路;V2k为施加到电池单元的电压;V0k为次级绕组的电压;L1k、C0k、C1k为通用滤波器的电感和电容;L0k、C2k分别为次级绕组的漏电感和电池的电容。

滤波器产生的增益幅度随开关频率的变化而变化,在一定频率范围内增益有2个峰值频率ωp1、ωp2,其表达式为:

(16)

由于电池单元的电容远高于其他值,第1峰值频率仅受单元电容的影响,第2峰值频率仅受滤波器电容的影响。

若另一种绕组数偏少,则会产生偏低的正向输出电压。对于这种情况,利用通用滤波器与上述相反的特性,经拉普拉斯变换后其传递函数公式为:

A=L0kL1kC1kC2k,

B=L1kC1k+L1kC2k+L0kC2k

(17)

滤波器产生的增益随开关频率的变化而变化,在一定频率范围内滤波器的增益有3个峰值频率,其中ωP1′和ωP2′与通用滤波器频带放大功能具有相似的特性,则ωP1′和ωP2′与公式(16)相同,ωP3值的表达式为:

(18)

ωP3的值是传递函数二阶零点,该频率处的增益幅度表示与其他峰值频率相比的相反特性。随着频率的变化，滤波器增益受电容器等效串联电阻(equivalent series resistance,ESR)和电感器的直流电阻(directive current resistance,DCR)的限制。

除电容值不同外,这些滤波器其他参数均相同。由于电池电容值相近,各滤波器的第1峰值频率相似;而由于滤波器的电容值不同,第2峰值频率是不相等的。

根据滤波器的电容值大小,每个滤波器在特定频率下显示不同的增益。

3 均衡策略

3.1 滤波器设计

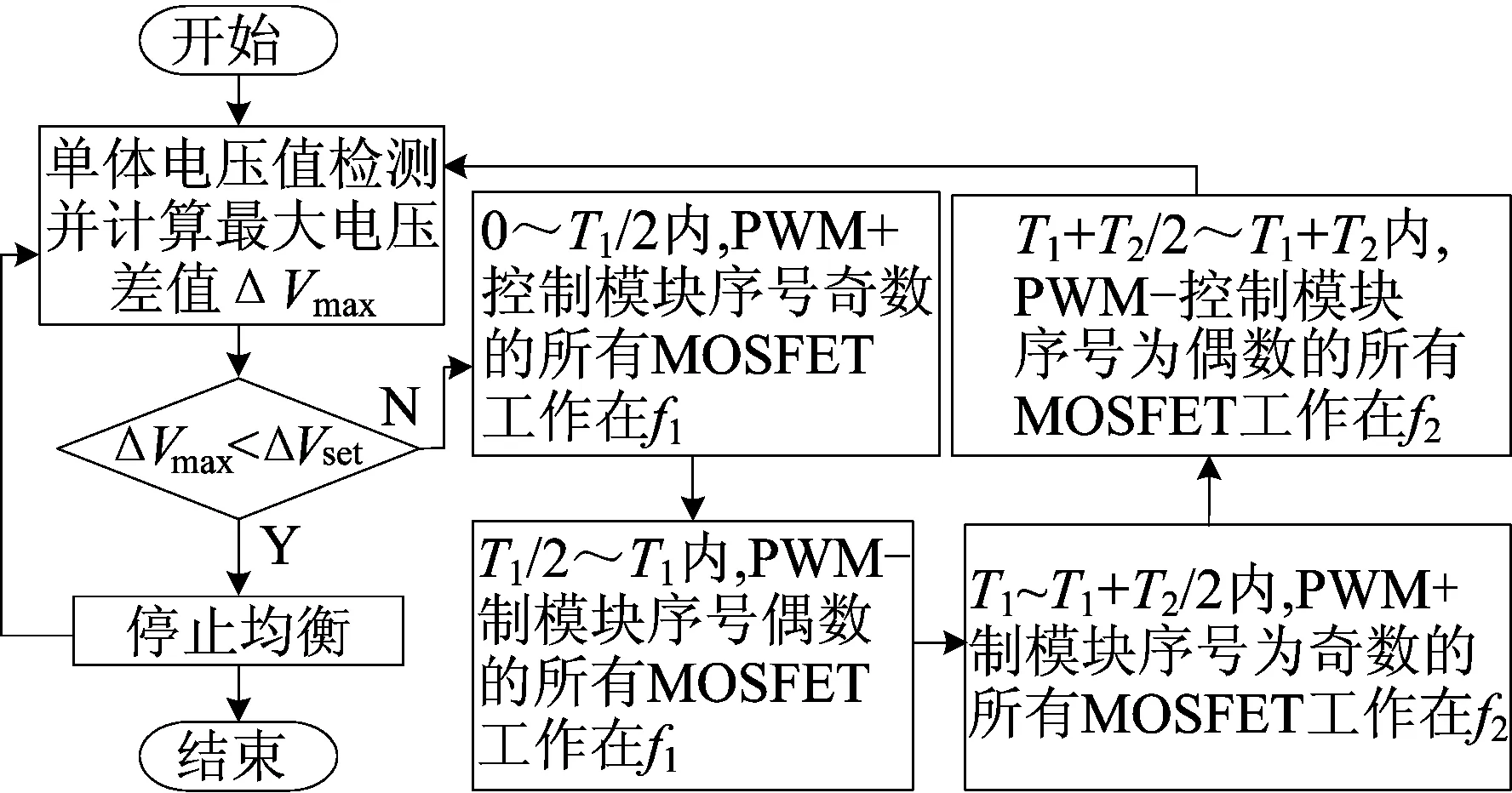
理论上,本文所提出的电池组均衡器可以通过给每个单元电路中通用滤波器设计特定信号发生器,使均衡电路中所有的MOSFET能以固定的占空比、不同的频率进行工作,从而完全消除变压器绕组不均匀现象。而实际上,为均衡电路增加设计N个信号发生器,不仅会使均衡策略变得难以实现,而且拓扑也更加复杂。因此本文考虑现实情况,提出近似消除法来降低变压器绕组匝数比不均匀带来的不利影响。

近似消除法是通过设计2个信号发生器形成一对互补的PWM控制信号(PWM+,PWM-),通过变频来实现高通滤波器和低通滤波器的功能。具体步骤如下:

(1) 整个均衡电路中所有模块的初级侧绕组从上至下依此进行标号i(i=1,2,…,N),测量每一个初级侧绕组正常运作时的直接输出电压，记为Vi,并求出所有绕组电压均值Va,即

(19)

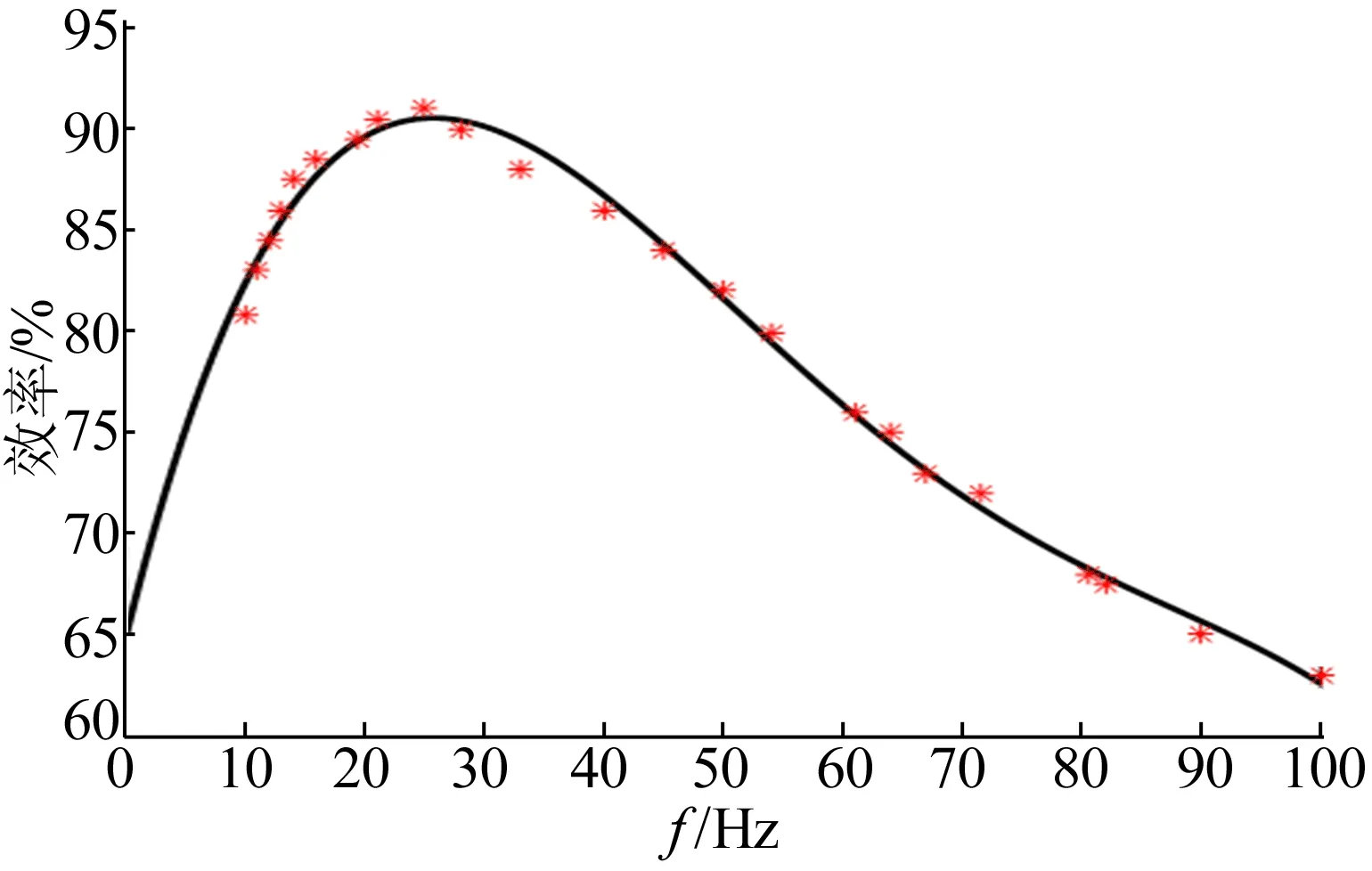
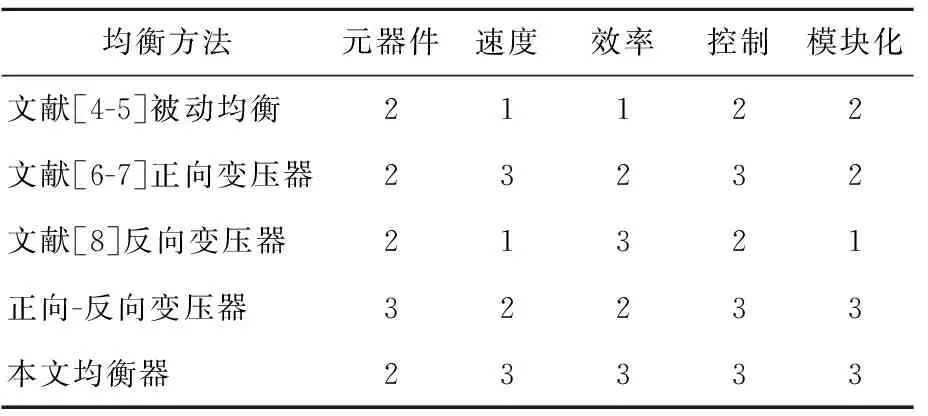
(2) 整个均衡电路中，所有模块的初级侧电路分为2类：第1类为衰减型电路,第2类为放大型电路。若Vi

(3) 上述电路划分完毕后,设计电路均衡器时,为第1类电路的单元电路设计放大型CL滤波器,为第2类电路的单元电路设计衰减型LC滤波器。

3.2 控制策略

本文提出的均衡器控制电路与传统的均衡控制方法不同,通过电压检测电路检测均衡电路中所有单体电池电压,并计算出最大的单体电池间电压差ΔVmax。

若最大单体电池电压差ΔVmax大于预先设定的停止工作电压差值ΔVset,则停止均衡;否则均衡器继续工作。

均衡的整体流程如图6所示。

图6 均衡整体流程

每个均衡周期具体的均衡过程如下:

(1) 将均衡电路中的模块按照序号1、2、3、……、n依次进行标号,使互补控制信号中PWM+以高频f1(放大型滤波器工作频率)控制均衡电路中模块序号为奇数的所有MOSFET开关接通,并开始均衡。

(2)T1/2周期,PWM+信号控制的MOSFET开关关断,使互补控制信号中PWM-以高频f1控制均衡电路中模块序号为偶数的所有MOSFET开关接通,并开始均衡。

(3)T1～T1+T2/2周期,PWM-信号控制的MOSFET开关断开,使得PWM+以低频f2(衰减型滤波器工作频率)控制均衡电路中模块序号为奇数的所有MOSFET开关接通,并开始均衡。

(4)T1+T2/2～T1+T2周期,PWM+信号控制的MOSFET开关断开,使PWM-以低频f2控制均衡电路中模块序号为偶数的所有MOSFET开关接通,并开始均衡。T1+T2周期后返回步骤(1),循环执行。

4 实验与分析

为了验证本文所提出的均衡器对电池组均衡的效果,将该拓扑结构集成到课题组自行研制的电池测试平台台架进行实验,实施8个串联锂离子电池模型,并分为2个模块[15]。实验实施的原型和相关仪器如图7所示。

图7中:(a)为无纸记录仪;(b)为电子负载;(c)为信号发生器;(d)为可编程电源;(e)为电池组;(f)为均衡器。

图7 电池原型及相关仪器

本次实验在25 ℃恒温条件下进行,选择经过循环充放电500次的24节标称容量1 500 mA·h的18650磷酸铁锂电池作为均衡实验对象,并分成A、B、C 3个组。使用特殊信号发生器,它可以产生一对互补的变频PWM信号(PWM+,PWM-),且分别控制2个模块中的MOSFET。一般来说,占空比设计为50%,匝数比n为4,所有模块初级侧与次级侧绕组数分别为15、60 匝,初级侧磁化电感为150 μH,次级侧磁化电感为2 400 μH[12-13]。

本文均衡器均衡效率与工作频率之间的函数关系曲线如图8所示。

图8 效率与频率函数曲线

由图8可知,本文均衡器能实现在宽频率范围内均具有较高的均衡效率,频率范围在20～35 kHz内,效率均能保持在88%以上。

因此,在保证高效率的同时,结合本文提出的滤波器需要的2种工作频率控制,选定放大型滤波器工作频率为32 kHz,衰减型滤波器工作频率为24 kHz。

利用实验验证本文均衡器动静态均衡的有效性。M1、M2实验过程中关键电气量波形如图9所示。

从图9可以看出,M1、M2关键电气量的实验波形与理论波形相同。

图9 关键电气量波形

以A组8节串联电池进行静置均衡过程实验,实验结果如图10a所示。以B组8节串联电池进行充电均衡过程实验,实验结果如图10b所示。以C组8节串联电池进行放电均衡过程实验,实验结果如图10c所示。

图10 8节串联锂离子电池均衡实验

A组、B组、C组电池分别在大约5 500、3 000、5 500 s后达到均衡停止条件。每组电池均衡前、后各单体电池电压和各电池组最大电压差见表1所列。

表1 各单体电池均衡前、后电压及差值对比 单位:V

由表1可知,A组、B组和C组电池的最大电压差分别由均衡前495、356、193 mV减小到均衡后3、2、2 mV。因此,本文均衡器能将处于任何状态下的串联电池包的所有电池电压收敛在一起,以确保电池组具有最大的可用容量。

相较于文献[9-10]所提出的均衡电路,本文均衡器充电、放电及静置均衡后的电池组最大电压差分别由7、5、3 mV降至3、2、2 mV,说明通过改进Fly-back变压器实现了均衡精度的提升。因此,本文所提出的均衡器能极大地改善电池组在静置、充电和放电期间的一致性和可用容量,具有良好的动静态均衡性能。

将本文均衡方法与几种典型的均衡方法进行对比,结果见表2所列。

表2从均衡拓扑和均衡策略的角度考虑,选用元器件数量、均衡速度、均衡效率、均衡控制难易度、均衡模块化5个同等重要的均衡指标进行量化比较,为了简化对比过程,将各均衡指标通过“1、2、3”量化表示优劣等级,数字越大代表性能越好。

从表2的对比结果可以看出，本文提出的均衡器具有成本低、效率高、平衡速度快、易于模块化的明显优势[16]。

表2 电池均衡方法对比

5 结 论

本文基于多绕组变压器结构,提出了一种提升均衡精度且易扩展的任意单体到单体的电路结构。该方法在保证锂电池组充放电安全的前提下,在电池组动静态期间进行均衡,能良好地改善单体电池间的不一致,同时提高了电池组的充放电容量,并实现了所有功率器件上的低电压应力,提高了均衡电路的可靠性。此均衡电路应用在耗能大的电动公交车、运输车上具有很大优势,不仅能保证运行安全,而且能提升续航能力。

本文提出的均衡器在提高均衡精度方面仍有一定的提升空间。今后的研究分为2个方向:一是在所提出的均衡拓扑基础上,改进通用滤波器实施策略,进一步改善电池组间的不一致性;二是从电池组的热均衡入手,尤其是热均衡的集成管理方面,进一步提高均衡效率缩短均衡时间。