基于改进PFV策略的双车道连续元胞自动机模型*

赵子翔，彭勇，沙晓宇

(1.重庆交通大学 交通运输学院，重庆 400074；2.华设设计集团，江苏 南京 210002)

微观交通流仿真模型是研究交通问题的重要手段，元胞自动机模型能有效描绘交通流运转机理，探究道路中存在的交通问题。1992年，Nagel K.等将微观交通流仿真与元胞自动机相结合，提出经典的NaSch模型。随后大量学者在此基础上进一步展开研究。但传统元胞自动机模型将跟弛行为离散化，难以精细刻画道路交通流状态。为此，Öznur Yeldan等提出采用连续元胞自动机模型研究高速公路随机交通流，探究道路的连续性动态变化情况。基于该方法，彭勇等考虑多车影响的跟驰策略，构建了单车道连续元胞自动机模型。但现实中的道路由多条车道组成，行驶过程中车辆并非一直沿同一车道行驶，会出现换道行为，车辆跟弛不仅受到前后车的影响，还受到相邻车道车辆的影响，不宜将单车道连续元胞自动机模型直接应用于多车道交通流仿真分析。对于多车道跟弛策略，Ge H.X.等提出一种结合反馈控制的双车道跟驰策略，在跟驰策略中引入换道规则；夏冬雪等综合考虑各种因素对驾驶行为的影响，提出考虑相邻车道车辆和前方多辆车辆影响的双车道跟驰策略；Ou H.等提出一种考虑车间通信的双车道跟弛策略跟车模型。但在实际跟弛行为中，驾驶员通常会根据前后及相邻车道多车信息进行跟弛决策。该文考虑多车信息的跟驰策略，结合换道规则，构建双车道连续元胞自动机模型，并利用实际道路交通流数据对模型进行验证。

1 双车道连续元胞自动机模型

假设跟驰车队在一条双车道道路上行驶，将道路上的车辆视作元胞，车道路段长度L，元胞长度(车辆长度)l，路段的车辆承载力Nz=L/l。模型采用周期性边界条件。双车道元胞自动机模型仿真流程见图1。

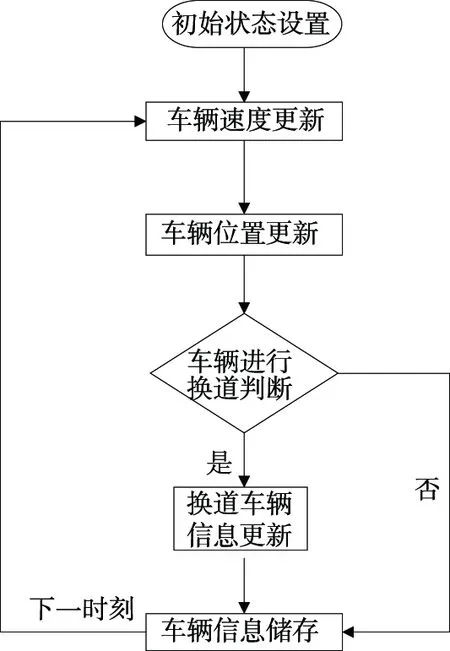
图1 双车道连续元胞自动机模型仿真流程

(1)初始车辆设置。每条车道车辆的初始位置和速度表达式如下：

xi,j(0)=(L/Na-l)rand(1)+

(L/Na)(i-1)+l

(1)

vi,j(0)=min(vmaxrand(1),di+1,j)，

vi,j(0)>0

(2)

式中：xi,j(0)为每条车道上车辆的初始位置；i为车辆编号；j为道路编号；Na为道路上初始车辆数；rand(1)表示生成0-1的随机函数；vi,j(0)为每条车道上车辆的初始速度；vmax为最大速度；di+1,j为当前车辆与前车的距离。

(2)速度更新。车辆速度更新规则如下：

vi,j(t+1)=min(vmax,di+1,j,vi,j(t)+

ai,j(t+1))

(3)

式中：vi,j(t+1)为车辆在t+1时刻的行驶速度；vi,j(t)为车辆在t时刻的速度；ai,j(t+1)为车辆在t+1时刻的加速度。

(3)车辆位置更新。更新规则如下：

xi,j(t+1)=xi.j(t)+vi.j(t+1)

(4)

式中：xi,j(t+1)为车辆在t+1时刻的位置信息；xi.j(t)为车辆在t时刻的位置信息；vi,j(t+1)为仿真步长为1 s时车辆行驶的距离。

(4)车辆换道。按换道策略进行换道决策。

2 跟驰和换道策略

2.1 跟驰规则

在PFV策略的基础上，综合考虑多车最优速度和前后车最优速度差的影响建立新的跟驰策略，表达式如下：

φV(Δxi+1,j(t))-vi,j(t)]+σΔvi,j(t)+

κ(V(Δxi+1,j(t))-V(Δxi,j(t)))

(5)

式中：V(·)为t时刻车辆i在车道j上的最优速度；Δvi,j(t)为t时刻车辆i在车道j上与前车的速度差；α、β、γ、φ、σ、κ为敏感系数。

采用Bando M.等提出的最优速度函数，表达式如下：

tanh(hc)]

(6)

式中：hc为安全距离。

选取文献[9]中NGSIM高速公路数据，采用遗传算法对跟驰策略参数进行标定。遗传算法种群规模为50个，交叉概率为0.9，变异概率为0.2，迭代次数为200次。目标函数Fobj如下：

(7)

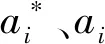
参数标定结果如下：α=0.521 4；β=0.542 3；γ=0.231 7；φ=0.123 1；σ=0.118 6；κ=0.098 4；Fobj=0.857 1。实测加速度与计算加速度对比见图2，标定计算出的加速度与实际加速度有较好的拟合度，跟弛策略能较好地反映跟弛行为。

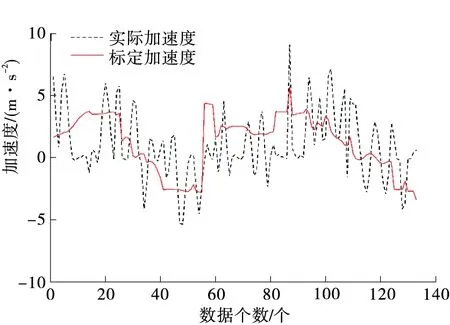
图2 标定加速度与实际加速度对比

2.2 换道规则

实际道路中有强制换道和非强制换道2种换道行为。当车辆与前方车辆的距离几乎小于安全距离时，车辆必须根据安全需要采取换道措施，这是一种强制换道行为。当车辆与前方车辆保持安全距离，但相邻车道车辆较少时，可选择是否换道，属于非强制换道行为。据此制定变道策略(见图3)如下：

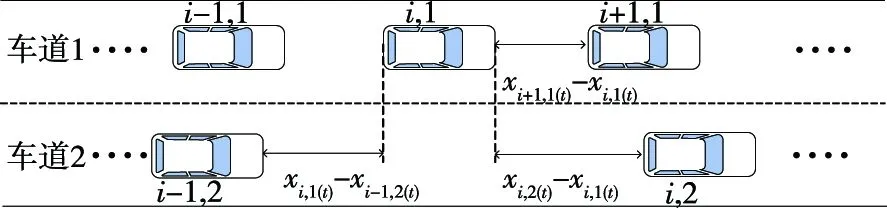
图3 车辆换道示意图

(1)车道1上车辆i与车辆i+1间距小于在时间步长Δt内车辆i行驶的距离时，车辆i产生换道意愿，即：

Dn<(vi,1(t)+ai,1(t)·Δt)·Δt

(8)

式中：Dn为车辆i与前车i+1之间的距离(m)；vi,1(t)为车辆i当前的速度(m/s)；ai,1(t)为车辆i当前的加速度(m/s2)；Δt为单位时间。

(2)车道1上车辆i产生换道意愿后，当满足车辆i与相邻车道上前车的间距大于在时间步长Δt内车道1上车辆i行驶的距离与安全距离dsafe之和，且车辆i与目标车道上后车的间距大于在时间步长Δt内目标车道上后车行驶的距离与安全距离dsafe之和时，产生实际换道行为，即：

DQ>(vi,1(t)+ai,1(t)·Δt)·Δt+dsafe

DH>(vi-1,2(t)+ai-1,2(t)·Δt)·Δt+dsafe

(9)

式中：DQ为换道车辆与目标车道前车之间的距离(m)；dsafe为车辆之间的最小安全距离(m)；DH为换道车辆与目标车道后车间的距离(m)；vi-1,2(t)为目标车道后车的速度(m/s)；ai-1,2(t)为目标车道后车的加速度(m/s2)。

(3)根据2种换道行为的情况，加入换道概率ps，如果车辆与前方车辆保持相当大的安全距离，仍有可能产生换道意图，然后重复第二步判断是否存在换道条件进行换道。符合换道条件的车辆换道至目标车道，不符合换道条件的车辆不换道。当车辆横向移动时，保持换道前的速度和加速度，然后根据跟驰规则更新行驶状态。

3 仿真分析

3.1 仿真设置

仿真时长为5 000 s，2条车道初始车辆数相同(Na=100辆)，车辆长度l=5 m，最大车速vmax=30 m/s，最大加速度amax=6 m/s2，换道概率ps=0.6。

3.2 仿真结果分析

如图4所示，当交通流密度小于0.05 veh/m时，仿真结果较好；当交通流密度大于0.05 veh/m时，仿真结果比实际数据略高。总体来讲，仿真结果与实际数据的拟合程度较好，说明基于上述跟驰-换道策略建立的双车道连续元胞自动机模型合理，能用于交通流仿真。

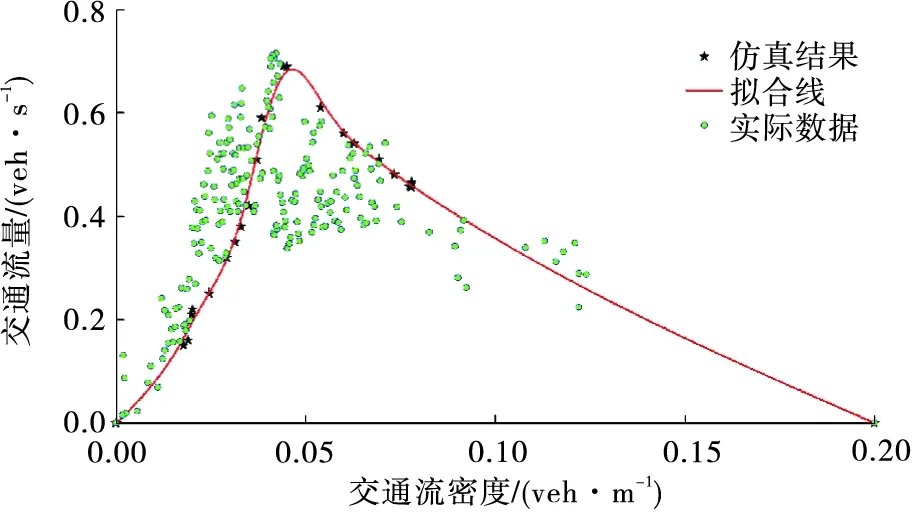
图4 实际数据与仿真结果对比

图5为车辆平均速度仿真结果。车辆根据跟驰策略和换道规则进行车速更新与调整，车道1与车道2车速相差不大，车速在26 m/s上下波动，道路总体情况较通畅，仿真效果与模型设置情况相符。

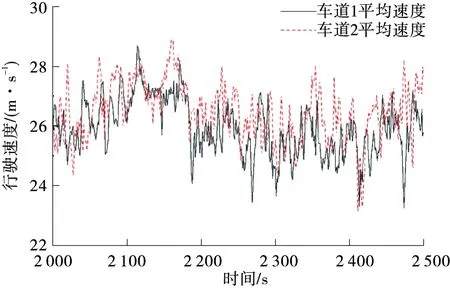
图5 双车道连续元胞自动机仿真平均速度

根据图4仿真结果，分别选取交通流密度0.02、0.06 veh/m，比较分析在交通状况良好和交通状况较拥堵情况下双车道交通流情况。图6、图7为不同交通流密度下仿真时空图，图中的点代表当前时刻车辆所处位置，可通过点的密集程度判断道路的拥堵情况。

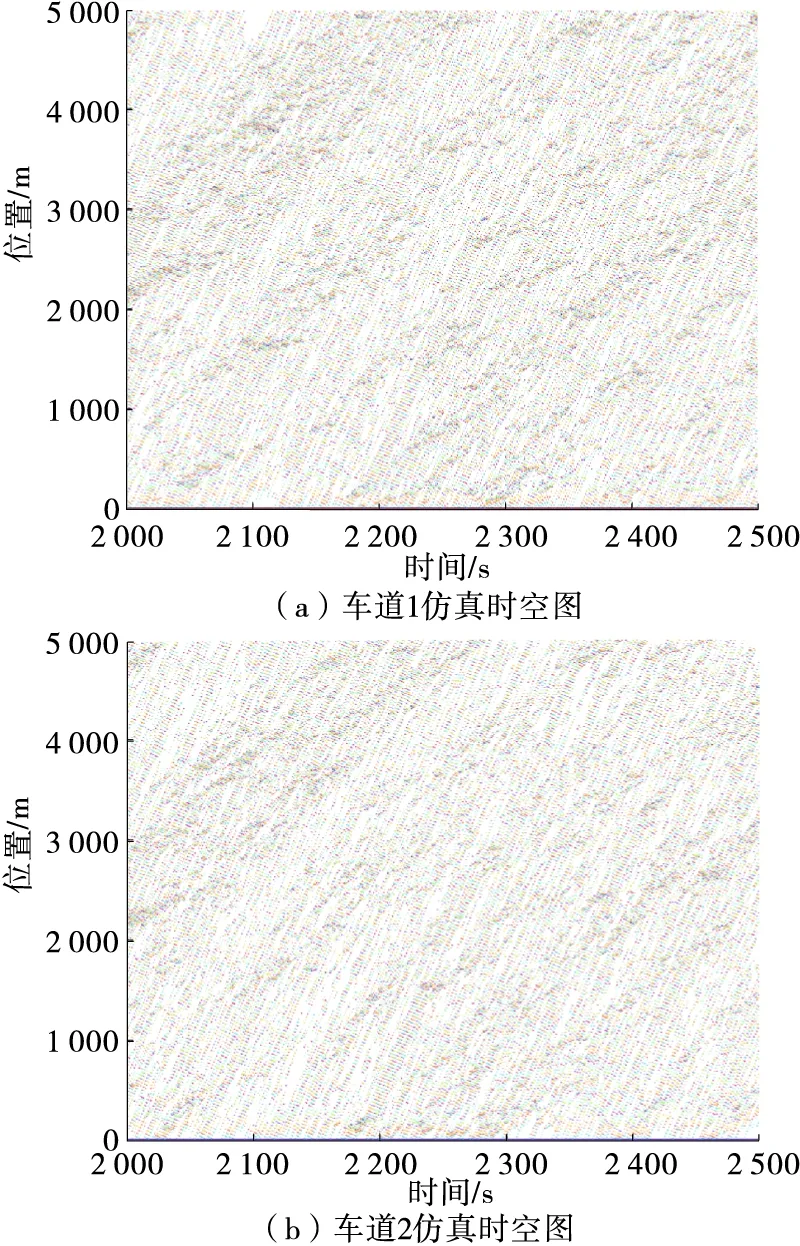
图6 交通流密度为0.02 veh/m时双车道时空图

由图6可知：交通流密度为0.02 veh/m时，车辆具有良好的行驶条件，车辆换道条件充分。仿真结束，统计2条车道通车情况，共有5 145 辆车通过路段终点。车辆换道会对目标车道上车辆造成一定影响，使目标车道上车辆出现一定减速，且减速情况向车流下游传递。车道1和车道2上车辆的平均速度分别为24.98、25.56 m/s，平均速度没有发生明显变化，整体通行较顺畅。考虑跟驰与换道策略的仿真结果更符合实际情况。

由图7可知：由于交通流密度增加，道路行驶状况较差，换道条件不充足，极大减少了非强制换道次数，同时由于交通流密度较大，系统整体运行速度有所降低。在总仿真时长内，车道1、车道2上车辆的平均速度分别为11.82、11.51 m/s，与交通流密度为0.02 veh/m时相比，道路通行效率明显下降，且由于车辆换道造成拥堵和延误。在交通流密度较大的情况下，车辆的通行效率和换道次数都明显下降，仿真结果与实际道路运行规律较相符。

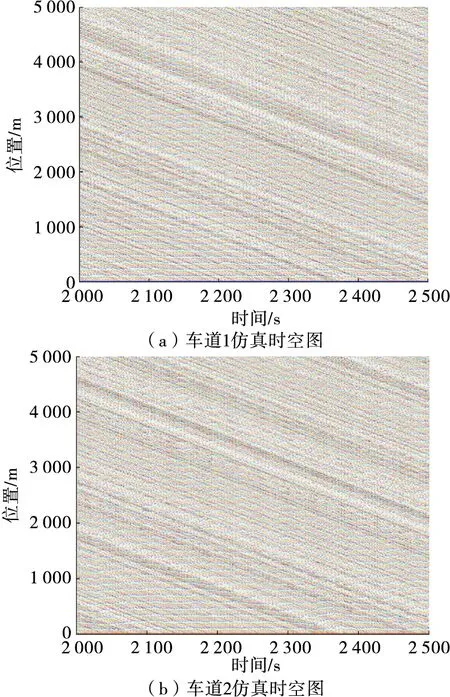
图7 交通流密度为0.06 veh/m时双车道时空图

平均速度与交通流密度的关系见图8。由图8可知：速度-交通流密度关系曲线的趋势与现实交通情况相符。交通流密度小于0.02 veh/m时，道路上的车辆行驶状况很好，车辆可在本车道上以最大速度行驶，不需要通过换道就可获得更好的速度，故车辆的平均速度无明显变化。密度为0.02～0.08 veh/m时，3条曲线存在明显差别，此时交通流密度适中，道路中具备一定换道条件，车辆会通过换道来获得更优的行驶速度，故车辆会有较多的换道行为，导致两车道平均速度存在差异，与仿真设置的双车道模型行驶条件相符。密度大于0.1 veh/m时，3条曲线基本重合，平均速度与密度关系基本没有变化。在交通流密度过大时，行驶在道路上的车辆没有足够的换道条件，大部分车辆不发生换道行为。

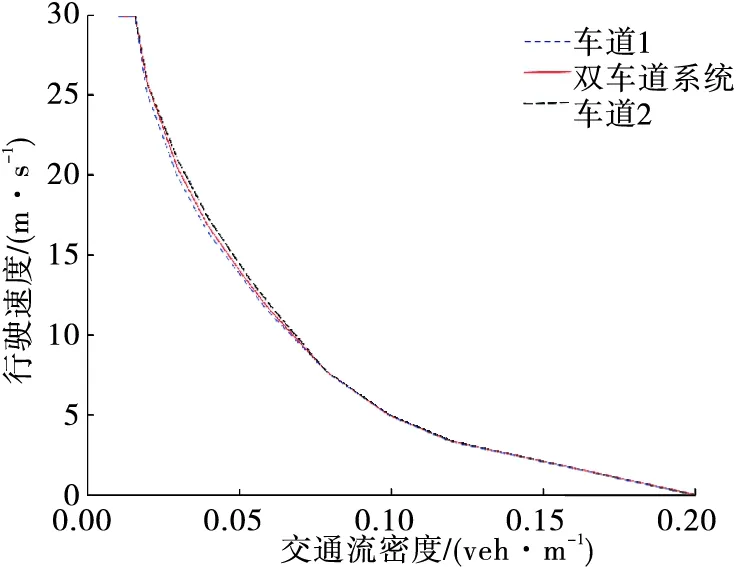
图8 单条车道与系统整体的速度-密度关系

4 结语

将考虑多车信息的跟驰策略与换道策略相结合，建立双车道连续元胞自动机模型，通过对模型进行模拟仿真，验证模型的适用性和合理性，并探究交通流特性。通过仿真对比不同交通流密度下车辆时空变化，描绘不同密度下双车道上车辆换道情况；通过分析对比双车道的交通流三要素指标，证明所建双车道连续元胞自动机模型与实际道路情况相符，能应用于实际交通流问题研究。