快速路上交通事件所致延迟的实时预测*
2022-03-04李翠张春雨
李翠,张春雨
(江西交通职业技术学院 信息工程系,江西 南昌 330013)
为保证快速路的正常通行能力,路上发生的各种交通事件(如车辆刮蹭、货物洒落、车辆抛锚等)应得到及时处理。除交通事件的及时侦测外,交通延迟的实时预测也是交通管理部门的重要需求。交通延迟的预测方法大致分为波动法和队列法。波动法引入冲击波、扰动清除时间和最大队列长度等构造由交通事件引起的交通流时空变化模型,其理论模型较精细,需要大量数据支撑。队列法通过计算到达曲线和离开曲线围合的面积得到总的交通延迟,意义明确、计算简单。队列法又可分为确定性队列法和随机性队列法,前者参数(如到达曲线、交通事件持续时间、离开曲线等)均为已知常数,而后者将各种参数视作随机变量。确定性队列法只给出确定的交通延迟预测结果,预测精度往往较差,且只能用于事后评估分析。随机性队列法能给出具有一定保证率的交通延迟预测结果,可用于实时预测,但计算较复杂。因此,有必要开发可兼顾预测实时性和计算简便性的交通延迟预测新方法。为实时预测快速路上由交通事件引起的交通延迟,该文提出改进队列法,并通过算例分析验证其有效性和实用性。
1 队列法的基本原理
如图1所示,S1表示交通事件被清除后的通行能力,S2表示输入事件地点的平均速率,S3表示事件持续时间内道路的通行能力,T1表示交通事件从发生到被清除(或称结束)所持续的时间,T2表示交通事件从发生到道路通行恢复正常所经历的时间,dmax表示个体车辆的最大延迟。S2对应到达曲线,表示交通需求;S1和S3对应离开曲线,表示通行能力(或服务能力)。
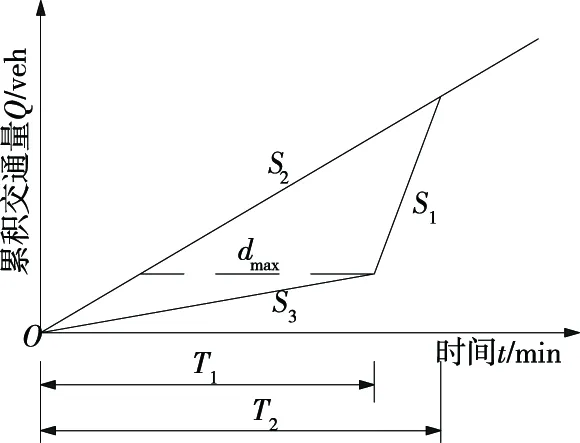
图1 队列法计算交通延迟示意图
到达曲线、离开曲线和事件持续时间均为已知常量,到达曲线和离开曲线围合的面积即为交通总延迟,其数学表达式为:
(1)
对于在时刻t流入事件地点的个体车辆,其时间延迟为:
(2)
式中:T2按式(3)计算。
(3)
根据图1,当个体车辆在时刻t=S3T1/S2到达事件地点时,其离开事件地点的延迟最大,为:
(4)
式(1)~(4)描述的是确定性队列法。该方法计算简单,但要求各参数均为已知,故只适用于交通事件被清除后的评估分析。如果对以往积累的交通事件数据进行统计分析,可考虑事件持续时间的随机变化对交通延迟的影响,也可进一步考虑到达曲线和离开曲线的随机变化,从而构成完整的随机性队列法。随机性队列法引入概率思想对交通延迟进行分析,计算较复杂。
2 改进队列法
为实时预测快速路上交通事件所致延迟,对传统队列法进行改进。基本思路为:1)基于上游监测断面采集的交通量信息,利用K近邻法对到达曲线进行预测;2)利用线性回归方法估计交通事件的持续时间;3)将下游监测断面采集的交通量信息和路段的最大通行能力相结合对离开曲线进行拟合;4)参照确定性队列法预测交通延迟。
图2为改进队列法计算交通延迟示意图。与图1相比,到达曲线不再为直线,而是呈波浪上升的曲线。到达曲线可根据上游监测断面采集的交通量信息,利用K近邻法(或其他预测方法)进行预测得到。离开曲线依然为2段折线,第1段折线根据下游监测断面短时采集的交通量信息进行平均处理后得到,第2段折线为路段的正常通行能力。在利用线性回归方法预测事件持续时间的基础上,将2段折线相连便得到拟合的离开曲线。S2仍然对应到达曲线,但为不断变化的速率;S1和S3对应离开曲线,均为平均速率。此外,到达曲线并非直线,而是由离散的多个采样点相连而成。
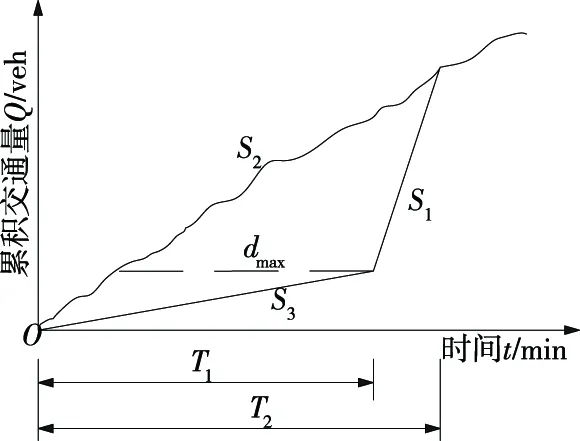
图2 改进队列法计算交通延迟示意图
对式(1)~(4)进行修改以获得准确的交通延迟计算结果。通过寻找到达曲线和离开曲线的交点(此时到达曲线的累积交通量为QT2),得到T2:
(5)
由于到达曲线由离散采样点连接而成,到达曲线与离开曲线的交点可能在2个采样点之间。因此,采用简单的线性插值法在2个采样点之间的交点处增加1个虚拟采样点,对应QT2和T2。
通过计算到达曲线和离开曲线围合的面积,得到交通总延迟:
T1)2-S3T1(T2-T1)
(6)
式中:N为0~T2时段内采样点数量(包括虚拟采样点);Qi为第i个采样点对应的累积输入交通量;Δti为到达曲线第i个采样点对应的采样间隔。
同理,作1条累积交通量等于S3T1的水平线,在该水平线与到达曲线的交点处采用线性插值法新增1个虚拟采样点,该虚拟采样点对应的累积交通量和时刻分别记为QT3、T3,则对于在时刻t流入事件地点的个体车辆,其时间延迟为:
(7)
式中:Q(t)为到达曲线在t时刻的累积输入交通量。
由于到达曲线不再为直线,不能直观判断个体车辆的最大延迟。可基于式(7)计算的所有采样点延迟按式(8)提取个体车辆的最大延迟。
dmax=max(di);i=1,2,3,…,N
(8)
改进队列法参照确定性队列法进行计算,但引入到达曲线、事件持续时间和离开曲线的预测结果,既可参照确定性队列法进行简单计算,又能保证实时预测功能。若以若干分钟为间隔进行更新,随着时间的增长,即可提供更准确的实时预测结果。
3 算例分析
假设某快速路上发生交通事件并被及时发现,定义此时为零时刻。根据交通事件的性质、天气状况等,经线性回归得到交通持续时间预测值T1=30 min。假设采样间隔Δt=3 min,S1=6 000 veh/h,S3=2 000 veh/h。上游监测断面的预测交通流量及其他相关数据见表1。
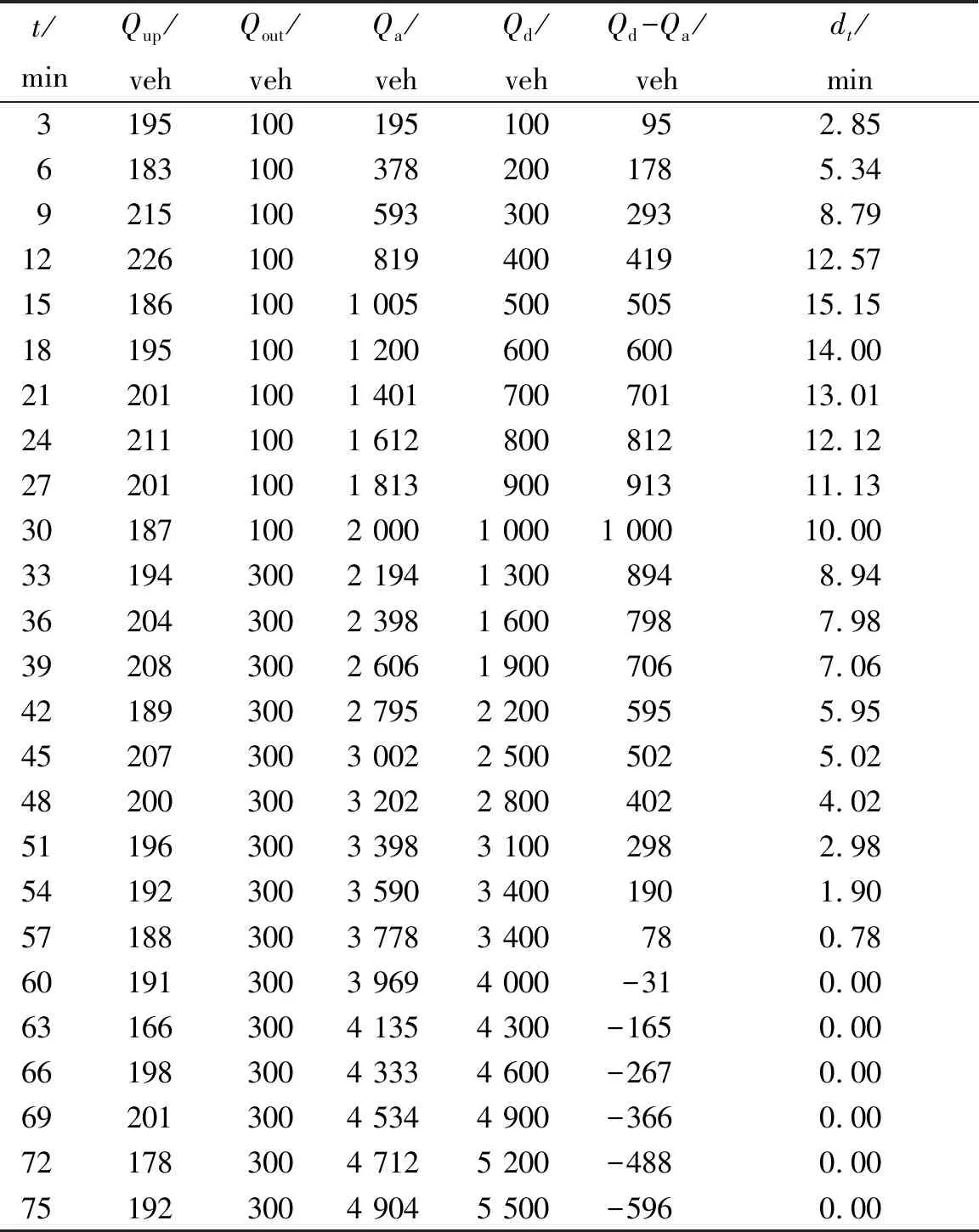
表1 上游监测断面的预测交通流量及其他相关数据
根据表1中积压交通量数据,在57~60 min存在1个虚拟采样点(即到达曲线与离开曲线的交点)。经线性插值得到T2=57.15 min。根据式(6)得到总延迟Dtotal=30 837 veh·min,根据式(7)得到个体车辆在各输入时刻的个体延迟dt,根据式(8)得到个体车辆最大延迟dmax=15.15 min。
1个采样间隔后,根据上游监测断面采集的输入交通流数据更新Qup和Qa,根据下游监测断面采集的输入交通流数据更新S3、Qout和Qd,并更新交通事件影响消散时间T2、总延迟Dtotal、个体车辆延迟dt及个体车辆最大延迟dmax。以此类推,不断实时更新交通延迟的预测值。
4 结语
确定性队列法计算简单,但只能用于事后的评估分析。随机性队列法能给出具有一定保证率的交通延迟预测结果,但计算较复杂。改进队列法引入到达曲线、事件持续时间和离开曲线的预测结果,既可参照确定性队列法进行简单计算,又能提供实时预测功能,其实用性强,具有较大的应用潜力。
