纳米MgO掺杂聚乙烯微观特性的分子动力学模拟研究
2022-03-04李亚莎胡豁然李光竹刘清东
李亚莎, 胡豁然, 夏 宇, 李光竹, 刘清东
(三峡大学 电气与新能源学院,宜昌 443002)
1 引 言
聚乙烯电缆因其具有优异的导电性能、机械性能以及耐环境应力而备受关注,自问世以来就广泛应用于高压输电线路和配电网中.然而随着现代电力工业的急速发展,日益增加的用电需求迫使电力电缆的传动性和安全性需要有高度保障,聚乙烯材料易变形、不耐热的缺点也随之放大[1].长时间的热老化作用以及水分子的渗透会使聚乙烯内部产生缺陷或结构性破坏,降低聚乙烯材料的绝缘性能[2-4].
为了解决这一系列问题,人们提出聚合物无机纳米复合材料,借助纳米颗粒的某些优良特性来改善聚合物的性能[5].纳米颗粒本身具有独特的小尺寸效应、表面界面效应以及量子效应而使得其不仅能提高复合材料的耐直流击穿能力,同时也能提高复合材料的力学性能等特性[6-8].赵等人[9]将硅烷偶联处理后的MgO与LDPE共混制得MgO/LDPE纳米复合材料,通过测试发现质量分数为4%的纳米MgO填料能有效抑制空间电荷的注入,且复合介质可以抑制电树枝的引发和生长.王有元等采用MgO、ZnO、SiO2三种纳米氧化物颗粒为填料对LDPE进行改性[10].结果表明,掺杂MgO使得LDPE具有最佳的抗氧化性和热氧老化防护效果.然而因为纳米颗粒尺寸过于微小,且绝缘材料的诸多优异性能由纳米复合材料的界面结构[11]决定,复合材料的微观理化过程无法通过实验从分子层面获取,分子模拟技术相比而言在微观研究方面有得天独厚的优势与潜力[12].
在高电压与绝缘技术领域内,常利用分子模拟技术仿真计算绝缘体系在特定温度或电场等状况下的反应过程,从微观机制角度去揭示绝缘材料的劣化与损坏过程.以分子动力学(MD)为依据对聚乙烯/蒙脱土纳米复合材料的研究发现,蒙脱土改性聚乙烯会产生氢键作用,使材料结构更加稳定,同时力学性能也有所改善[8].王等人[10]同样在实验的基础上进一步借助分子动力学模拟计算纳米颗粒和材料分子链之间的相互作用,并研究纳米颗粒对材料内部氧气扩散速率的影响,发现纳米颗粒通过抑制重结晶和氧气扩散的作用延后了热氧老化反应发生的时间,起到了热氧老化防护的效果.凡等人[13]研究了LDPE、纳米SiO2以及水分的复合模拟模型,结果表明水分会降低材料的玻璃转化温度,纳米SiO2的加入则会提升其玻璃转化温度,增强复合材料热稳定性.然而对于低密度聚乙烯掺杂MgO后,其热稳定性以及水分子渗透能力变化的研究鲜有报道.
本文基于MD模拟方法对比研究了不同纳米颗粒半径的MgO团簇改性LDPE复合体系的玻璃化温度、分子链运动以及水分子的渗透系数,研究结果可为LDPE的热老化实验和抑制水树枝等方面提供参考.
2 计算模型和方法
高压电力电缆的主要绝缘材料为聚乙烯,聚乙烯则是由结晶区和无定形区两种存在形式构成的两相结构.结晶区的微晶因排列紧密,相互之间结合力大,从而具有较高的机械强度,相对于无定形区更为稳定不易被破坏,故建立纳米氧化镁掺杂聚乙烯模型时优先考虑无定形区.一般而言,聚乙烯因为吸水性小的特性,水分子不易渗透到聚乙烯绝缘层中,然而无定形区是最容易吸水和融入杂质的地方,在潮湿的环境中,水分在电场的作用下会经材料的无定形区渗入到材料内部的自由体积空穴中逐渐形成水树枝,导致电力设备尤其是高压电力电缆绝缘破坏.因此本文在构建模型时,为了对比研究MgO纳米团簇和水分对聚乙烯的性能影响,分别建立了不同种类的复合体系.
2.1 模型的构建
为了对比研究MgO纳米团簇和水分对聚乙烯的影响,综合考虑实际情况和模拟需要耗费的时间,本文采用Materials Studio 17.1构建和计算了不同类型的聚乙烯无定形区模型,分别为纯聚乙烯(PE)模型、MgO/PE模型、含有相同水分含量的PE模型和MgO/PE模型.不失一般性,为了计算方便,基于一个聚合度为120的聚乙烯分子单链利用Amorphous Cell模块构建无定形区复合模型.综合考虑构建模型的尺寸以及MgO纳米团簇在模型中所占的质量分数和自由体积,同时为了对比分析不同纳米颗粒半径的MgO对复合模型微观特性的影响,纳米MgO的颗粒半径分别设置为3 Å和5 Å.为使模拟结果不仅能反映真实聚乙烯的性质,并尽量减少链端作用,遂以5条聚乙烯单链构建的基体进行掺杂.在实际中,初始制备的纳米MgO表面存在不饱和的化学键,置于空气中会与O2和H2O发生反应,从而处于稳定状态.为了接近实际情况,需要对纳米团簇进行氧化处理,即对纳米团簇表面不饱和的O原子进行H处理,不饱和的MgO原子进行-OH处理.有相关研究表明,聚乙烯材料内的水分含量可达1%以上[14].因此在构建模型时考虑水分子在模型中所占的自由体积和质量分数,并且为了避免因水分含量不同而造成的影响,需要确保每个含水的复合模型中水分所占的质量分数均约为1%左右,即在复合模型中分别加入10个水分子.则构建PE、PE-10H2O、PE-MgO(3 Å)、PE-MgO(3 Å)-10H2O、PE-MgO(5 Å)、PE-MgO(5 Å)-10H2O六个复合体系模型,如图1所示.
2.2 MD模拟
为了使建立的六个模型达到最稳定的初始状态,首先,使用Forcite模块中的Geometry Optimization对复合模型进行结构优化以及能量最小化计算,选择正则系综(NVT)和等温等压系综(NPT)依次对体系进行一次分子动力学弛豫使其处于平衡状态,2次模拟的时长为200 ps,温度为300 K,压强为0.1 MPa.在此工况下对复合体系进行从100 K到600 K的5次循环退火处理,温度间隔为50 K,每个循环周期的模拟时间为100 ps,系综为NVT,并在每一步退火处理中都进行模型能量最小化.经过以上处理,使得构建的无定形模型中产生的局部最小值的势阱得以消除,使材料构型更加合理,并为进行下一步分子动力学模拟提供了比较合理的平衡几何构象.然后提取退火处理后能量最小的结构构象,先进行200 ps的NVT系综下的动力学模拟,将模型升温至600 K,再进行200 ps的NPT系综下的动力学模拟获取此温度下的参数,随后以50 K为梯度使用NVT系综按100 ps的模拟时长将模型的热力学温度依次降温至100 K,并在相同的目标温度下又进行200 ps的NPT模拟.在以上过程中,积分步长均设置为1 fs,压强设置为0.1 MPa,体系内各原子的动力学信息每隔200 fs收集一次.考虑体系在新温度点下需要重新平衡的问题,遂提取NPT系综下后100 ps的模拟数据用于分析.
整个模拟采用COMPASS力场[15],此力场是把以往分别处理的有机分子体系的力场与无机分子体系的力场统一的分子力场,已被证实非常适合有机分子和无机分子构成的体系.温度控制采用Anderse热浴法[16],压强控制采用Berendsen压浴法[17],牛顿运动方程的求解采用Velocity Verlet跳蛙算法.对于非键相互作用,范德华作用采用Atom Based方法[18],静电作用采用Ewald法[19].
3 仿真结果及分析
3.1 玻璃化温度分析
很多高分子材料都存在着结晶区和无定形区,其无定形区就属于玻璃态物质.玻璃化转变温度(Tg)是指非晶区中聚合物由“玻璃态”转变为“高弹态”的一个转折温度,也是无定形聚合物大分子链段自由运动的最低温度.一旦聚合物开始由平衡转变为链段运动,其多项性质也会发生显著变化,例如自由体积、膨胀系数、弹性模量、介电常数等,因此玻璃化转变温度是高聚物材料稳定性的重要评判指标.微观分子动力学模拟中确立玻璃化温度Tg最常用的可靠方法是比体积-温度曲线法,该方法采用NPT模拟取得各温度点下体系的比体积对温度数据作散点图,然后以拐点两侧的数据作分段线性拟合分别得到两条直线,直线交点的横坐标即为Tg,分析得到模型中的玻璃化温度如图2所示.
由图2可知,纯聚乙烯的Tg值比文献[20]低8 K,这主要是模拟时间和力场不同造成的,且与聚乙烯建模时初始构象的随机性有关,但并不影响对所有体系的对比分析.随着温度的升高,模型中比体积均在增大,且在玻璃转化温度附近出现跳变现象,即玻璃态向高弹态转化,分子链段开始运动的过程.其中不含水分的模型,即PE、PE-MgO(3 nm)、PE-MgO(5 nm)的Tg值分别为247 K、292 K、301 K,往模型中添加质量分数为1%的水分后,其Tg值分别变为232 K、274 K、282 K.对比各体系的Tg值可知水分会降低复合模型的玻璃转化温度,而掺杂MgO纳米颗粒则会提高PE的玻璃转化温度.玻璃转化温度的变化对应材料热稳定工作温度的变化,因此从这个意义上讲,水分会降低聚乙烯体系的热稳定性,而MgO则很好的提升了聚乙烯的热稳定性.
高分子材料内部的体积分为自由体积(VFV)和占有体积(VOV),被高分子材料自身原子或分子占据的体积是占有体积,具有原子尺寸的缺陷和由于原子无规则堆砌而产生的空穴的体积是自由体积.正是由于自由体积的存在,分子链才可能通过转动和位移而调整构象.根据Fox和Flory的自由体积理论[21]和分子运动理论可知,空穴是材料中微观粒子运动的重要原因之一,因此可以采用自由体积理论来解释绝缘材料内部分子的热稳定性和机械性能的变化.本文通过Material Studio软件中atom volumes & surfaces工具采用硬球探针法计算复合体系中介质即聚乙烯的自由体积分数(FFV),以PE+H2O为例,如图3所示.由于原子、分子之间具有相互作用,在此利用范德华半径为硬球探针,其具体数据如表1所示.
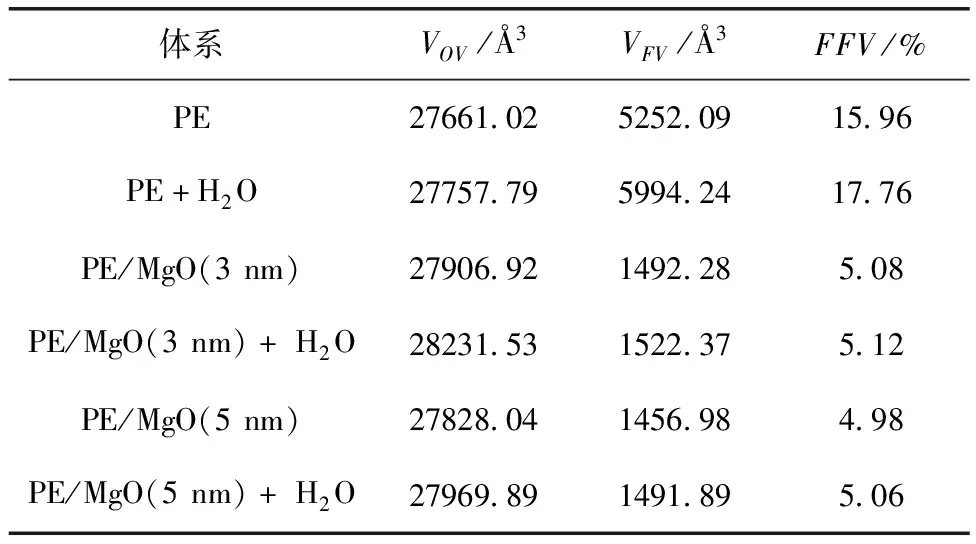
表1 300 K下各体系模型的VFV、VOV和FFV
表1为不同复合模型介质的占有体积VOV、自由体积VFV和自由体积分数FFV.从自由体积分数可以看出,水分子的加入使得聚乙烯的自由体积和自由体积分数均增大.自由体积的增大,必然会给聚乙烯的的链运动增加空间,水分子体积很小,对聚乙烯分子的链运动造成的空间阻碍也很小,并且因为聚乙烯分子链结构无羟基等亲水性集团,水分子与聚乙烯之间无法产生氢键,因此水分的加入会降低聚乙烯的玻璃化温度,起到增塑剂的作用.而MgO纳米团簇掺杂到聚乙烯中后,会填补聚乙烯原有的自由体积空隙,从而减小复合体系的自由体积,同时MgO与聚乙烯分子之间存在着一定的相互作用,都会减弱聚乙烯分子链的运动,并且氧化镁表面羟基与水分子之间形成氢键,水分子的运动强度得到抑制,使得复合体系的结构更加稳定,从而提高了体系的玻璃转化温度.
3.2 聚乙烯链运动
聚乙烯在玻璃化转变之前呈玻璃态,玻璃转变后呈高弹态,在高弹态阶段,链与链之间的阻碍作用减小,高分子链开始发生整体运动.聚乙烯的机械性能及热稳定性与聚乙烯的链运动有很大关系.聚乙烯链运动越强烈,聚乙烯的机械性能及热稳定性则越差.均方位移(MSD)能够描述链的整体运动情况,其计算公式如下所示:
MSD=〈|ri(t)-ri(0)|2〉
(1)
式中,ri(t)和ri(0)分别代表t时刻和初始时刻i分子或原子的位置向量,其中〈〉表示系综平均.
图4所示为不同温度下PE模型和PE-MgO(3 nm)模型中聚乙烯链的均方位移曲线.由图4可知随着温度的升高,两个体系聚乙烯链的MSD都在逐渐增大,说明温度的升高使得PE分子链的整体运动开始活跃起来.同时由图4可知,两个体系的MSD均出现了两次较为明显的跳变.对于纯PE模型第一次跳变出现在300~350 K之间,对于PE-MgO(3 nm)模型第一次跳变出现在350~400 K之间,均高于前述各体系的玻璃化转变温度,这正好说明模型从玻璃态向高弹态转变后聚乙烯分子链之间的相互阻碍作用减小,自由体积增大,链运动的自由度增加,整体移动加剧,从而导致模型的稳定性变弱.此外,两个体系分别在350~400 K和500~550 K出现第二次跳变,这可能对应着聚乙烯从高弹态到粘流态的转变.从整体来看,PE-MgO(3 nm)模型的均方位移数值明显小于PE模型中的均方位移的值,而且前者的均方位移出现一次跳变和二次跳变的温度范围均大于后者,进一步说明掺杂MgO纳米团簇能减弱聚乙烯的链运动强度,从而提升聚乙烯材料的热稳定性.模拟体系中分子链的运动和玻璃化转变过程之间的密切联系正好反映两者所具有的一致性.
3.3 水分子渗透
3.3.1基础理论
水分子在复合模型中的渗透能力可以通过计算水分子的溶解系数及扩散系数来进行表征.为了定量表征水分子在聚合物中的渗透系数,并且将溶解性及扩散速度定量化,渗透系数为
P=D×S
(2)
式中,P为渗透系数,表征水分子通过高分子膜难易度的一个重要参数,D为分子的扩散系数,反映渗透分子与聚合物体系的动力学特性,S为溶解度系数,反映渗透分子与聚合物相互作用的热力学特性.
(1)溶解度系数S是一个热力学参数,表示在渗透达平衡时,溶质在聚合物膜中渗透的物质量.分子在聚合物膜中的渗透过程一般采用溶解扩散理论来描述,聚合物膜的分离性能则由扩散系数和溶解度系数共同表征.在计算机模拟中,溶解系数通常通过蒙特卡洛统计力学方法[22]求得,有两种等效的方法进行计算.文中采用吸附等温线法,吸附等温线法是通过在一定的压力范围内进行一系列的巨正则蒙特卡洛(GCMC)模拟,得到吸附分子的浓度随压力变化的曲线,通常表现出非线性行为,可以通过dual-mode模型来描述[23]:
(3)
式中,C是偏压p下高分子中的平衡渗透物的浓度,其单位是cm3(STP)/cm3(聚合物),kD是Henry常数,CH是Langmuir容量参数,b是Langmuir亲和参数,表示气体分子吸附/解吸的能力.通过求出压力为零时的极限斜率,得到溶解系数S,即:
(4)
(2)分子动力学中水分子的扩散系数可以通过Einstein关系式[24]求解得到,公式为
(5)
由于模拟过程中已经对N个扩散原子数的MSD值作了平均,因此当模拟时间足够长时,扩散系数可以简化为如下形式:
D=m/6
(6)
其中m为MSD对t的曲线通过最小二乘拟合得到的直线的斜率.
3.3.2渗透机理分析
(1)图5是298 K时水分子在各个复合膜中的吸附等温曲线,由图可以看出,水分子在3种复合膜中的吸附等温线趋势相同.压力较低时,水分子以单分子形式优先在聚合物微孔区域被吸附,吸附速度较快;随着压力升高,水分子开始聚集成簇,且微孔区趋于饱和,水分子吸附在聚合物稠密区进行,速度变慢,并逐渐达到吸附平衡.分析图中各曲线可以看出,当压力相同时,纯聚乙烯膜内吸附的水分子个数最多,掺杂3 nm MgO的聚乙烯膜次之,5 nm MgO的最少.压力不同时,吸附在各个复合膜上的水分子个数随着压力的增大而增多,当压力增大到一定程度时,吸附分子的个数随压强的变化几乎不变,逐渐达到吸附平衡,且达到吸附平衡时在不同膜中的浓度值也有很大差别.
对其所得的数据采用最小二乘法进行拟合,结果如表2所示.表2给出了水分子在3种复合膜中的双重吸附模型参数及计算所得的溶解度系数.水分子在膜中吸附溶解过程受高分子链自由体积、水分子与高分子链相互作用等多种因素的共同影响.水分子在不同复合膜中的扩散系数和溶解度系数值差别较大,且溶解度系数大小顺序与复合膜自由体积分数大小顺序基本相同.

表2 300 K时水分子的双重吸附模型参数及溶解度系数
(2)以PE+H2O在不同温度下的水分子扩散为例,作出均方位移如图6所示,从图6中可以发现水分子在体系中的运动比较稳定,均方位移曲线与时间呈很好的线性关系,且随着温度的升高,水分子的均方位移和绝对值斜率均逐步上升.
对各体系水分子MSD曲线进行拟合求出不同温度下水分子在各模型中的扩散系数,如表3所示.

表3 不同温度下各模型中水分子的扩散系数(10-6cm2·s-1)
由表3中的数据可知,随着温度的升高,水分子热运动加剧,分子间的碰撞越强烈,所以扩散系数变大.水分子在聚合物体系中是不断随机运动的,但在大多数情况下作小幅度的振动,只有在合适的时候从一个自由体积空穴跳跃到另一自由体积空穴.由此可见体系内自由体积的大小、分布都对渗透分子的扩散有影响.自由体积分数越大,体系内的自由体积空穴越多,则渗透分子在体系内空穴间的跳跃所需的距离越小,扩散越快.这恰好是添加MgO纳米团簇会使水分子扩散系数降低的原因之一,另一个原因则是MgO纳米团簇能与水分子形成氢键从而抑制其扩散运动.由图6还可看出PE体系中水分子的均方位移在250 K~300 K之间有一个跳变,这与其玻璃化温度有关,也从侧面证明了玻璃化温度结果的准确性.
(3)对所得的水分子的扩散系数及溶解度系数进行运算,可得相应的渗透系数,如表4所示.表4给出了300 K时水分子在各体系中的溶解度系数、扩散系数及渗透系数.由表中可以看出,在相同温度下,水分子在三个体系中渗透系数的大小依次为PE、PE/MgO(3 nm)和PE/MgO(5 nm),渗透系数的变化趋势与溶解度系数和扩散系数的变化趋势是一致的,说明在水分子渗透过程中,渗透系数的大小主要由水分子对聚合物膜的溶解度系数和扩散系数值共同决定.水分子在掺杂纳米MgO的聚乙烯中的渗透能力小于纯聚乙烯,这是由于纳米MgO的加入占据了聚合物体系中的部分自由体积,变相减弱了水分子在聚乙烯体系内的溶解性与扩散能力,从而导致其渗透能力的减弱.

表4 300 K时水分子在3种模型中的溶解度系数、扩散系数及渗透系数
4 结 论
(1)利用经典的比体积-温度曲线法确定了各个聚乙烯复合模型的玻璃化温度.对于PE体系而言,掺杂水分使得其玻璃化温度下降了15 K,而MgO纳米团簇的加入则使得其玻璃化温度有所提升,且纳米MgO的颗粒半径越大,则复合模型的玻璃化温度提升的也越高,反映出水分会减弱聚乙烯的热稳定性,降低聚乙烯的热稳定温度工作点,纳米MgO则可以增强聚乙烯体系的热稳定性.
(2)聚乙烯分子链的均方位移随着温度的升高逐渐增大,并且随着温度的增加,分子链的均方位移增加的幅度也越大,并在不同的温度范围内均有两次明显的跳变,说明温度的升高不仅能使聚乙烯分子链的运动加剧,并且能引起聚乙烯分子结构从玻璃态向高弹态转变,进一步破坏聚乙烯结构的稳定性.添加MgO纳米团簇则能占据聚乙烯体系中的部分自由体积,有效抑制聚乙烯分子链的运动,从而提高聚乙烯体系的热稳定性.
(3)随着温度的升高,复合体系中水分子的扩散系数也逐渐增大,复合体系的自由体积越大,越有利于水分子的扩散.水分子在复合体系中的渗透能力由模拟得到的扩散系数和溶解度系数共同表征,纳米MgO的加入使得复合体系的自由体积分数变小,从而使其扩散系数和溶解度系数减小,因此导致水分子对聚乙烯的渗透能力减弱.
