不同潮汐水位下深厚滩涂软土路基长期沉降规律及预测研究

2022-03-04雷华阳万勇峰冯双喜

天津大学学报(自然科学与工程技术版) 2022年6期

雷华阳，万勇峰，冯双喜

(1. 天津大学建筑工程学院，天津 300354；2. 天津大学中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300354；3. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300354；4. 天津大学前沿技术研究院，天津 301700)

保护与开发并举是实现地区经济可持续发展的重要手段，滩涂作为沿海地区重要的土地后备资源受到广泛关注．《福建省海岸带保护与利用规划》中提到要加快沿海高速公路建设及城市轨道交通网络的发展，提升海岸带滩涂建设开发质量和综合效益，因此越来越多交通基础设施工程在我国东南沿海滩涂地区开始兴建[1-2]．滩涂区广泛分布着具有高含水量、高孔隙比、高压缩性、低强度、低渗透性软土地基．路基两侧赋存环境差别迥异，一侧邻接陆地(背水面一侧)，水位较低，一侧邻近大海(迎水面一侧)，长期受到潮汐水位影响．研究发现，在长期潮汐水位作用下，软土路基应力场和渗流场不断发生变化，容易引发工后沉降过大等工程事故[3-4]，甚至会直接影响工程的安全和正常使用，因此亟需研究潮汐水位下深厚滩涂软土路基长期沉降规律及预测，研究成果可为类似工程提供借鉴和指导．

与大型物理模型试验和现场试验相比，数值模拟具有计算效率高和计算成本低等优点，受到了广大学者的青睐．大部分学者利用数值模拟对路基沉降规律开展了系统的研究．宋金华等[5]利用ABAQUS阐述了路堤分层填筑过程中各点沉降随分层填筑高度增加而增大的变化规律．Kim等[6]采用应力-孔隙压力耦合模型的有限元分析方法，分析了地下水位变化对路基沉降的影响，提出了在设计中应考虑由于地下水位变化而引起的沉降．

潮汐水位下滩涂软土路基与浸水路堤类似，浸水路堤每年会遭受短期或长期的淹没．当水位上升时，水从边坡的一侧或两侧渗入路堤内，当水位降低时，水从堤内向外渗出．诸多学者通过室内试验和数值模拟开展了浸水路堤性能的研究．例如，陈伟志等[7]利用人工浸水方式开展了不同高度等尺寸路基现场浸水试验，研究了地基浸水后的变形特性，结果表明从路基填筑开始到人工浸水结束，地基的变形曲线呈现“S”型分布．付宏渊等[8]通过开展模拟路堤边坡外水位升高的室内模型试验，采用千分表测定坡顶的竖直及水平位移，研究了浸水条件下分层填筑路堤变形规律，结果表明路堤在水平方向的位移表现为先向坡内方向发展，后向坡外方向不断增大，竖直方向的变形表现为向下不断增大．李应涛[9]针对浸水路段的高填方路基开展了模型实验，提出水位高低和路基高度是影响浸水路堤变形与稳定的主要因素．张俊荣等[10]以两侧有水的浸水路堤为研究对象，采用有限元软件Geo-studio分析得到不同水位高度下路堤侧向位移主要集中在路堤中部，且随着水位高度增加而增大的结论．

针对路基沉降预测方法，根据其应用原理可以分为两类：一类是理论计算方法[11]，包括传统的分层总和法及根据固结原理结合土体本构模型的数值分析方法；另一类是基于实测数据的系统工程沉降预测方法[12-13]，如曲线拟合法、灰色理论法和神经网络法等.杨光华等[14]将基于e-p曲线和Duncan-Chang本构模型求取的非线性割线模量Ep应用于分层总和法，以此考虑软土侧向变形的非线性沉降计算．袁宇等[15]建立了反映时间效应的滨海软土三维非线性黏弹性蠕变本构模型，有效模拟了不同施工阶段路堤沉降量的非线性发展过程与沉降速率的变化规律．崔凯等[16]通过引入最小均方差法和最大关联度法判定最优拟合曲线，提高了沉降预测精度．Wei等[17]采用Newton-Cotes正交公式对背景值进行优化，提高了非等距灰色模型的适应性和拟合精度约30%．尹利华等[18]建立了考虑处理方法的地基沉降预测BP神经网络模型，证明了模型拟合精度可达95%以上．

综上所述，关于软土路基沉降规律的研究，大多数学者集中在未考虑潮汐作用的无潮汐水位或常水位工况，对潮汐水位下深厚滩涂路基长期沉降规律及长期沉降预测方法开展研究相对匮乏．本文基于福建某路基处理工程，结合现场沉降监测数据，通过数值计算对潮汐水位下深厚滩涂软土路基的长期沉降规律开展了系统研究，提出了一种综合考虑潮幅和周期的路基长期沉降预测公式，并研发了预测程序用来快速计算潮汐水位下路基的长期沉降，研究成果可用于指导类似工程实践．

1 工程概况

本路基工程位于福建省霞浦县境内，主线全长62.594km，软土路段分布范围广泛，约占全路段的49.2%．通过4组钻孔取样得到典型工程地质剖面如图1所示．从图1中可以看出，软土层厚度范围为9.8～12.0m，其物理力学性质参数如表1所示．从表1中可以看出，地层为具有高含水量、高孔隙比、高压缩性、低强度和低渗透性的呈流塑状态的海积淤泥．

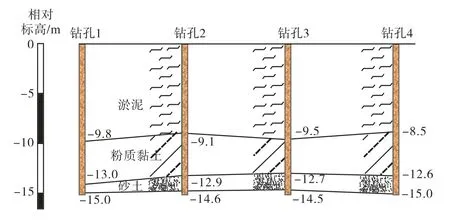
图1 典型工程地质剖面Fig.1 Typical engineering geological profile

表1 海积淤泥物理力学性质参数Tab.1 Physical-mechanical properties of the marine silt

软土路段主要为冲、海积滩涂地貌，地表多为滩涂和养殖区，多数软土路段承受潮汐水位影响，部分为正常路段，无水位变化．周期和潮幅是描述潮汐变化的两个特征指标，海水完成一次涨潮所用的时间称为潮汐周期，在一个潮汐周期内，相邻高潮位与低潮位间的差值称为潮幅．结合国家海洋信息中心发布的港口潮汐曲线图[19]，统计了30d内沿线路段各观测点高、低潮数据，得到该工程沿线路段水位最大潮幅可达2m，最小潮幅为0m，周期范围为0～5d．潮汐观测点位置及潮幅周期数据如图2和表2所示．截至目前本路基工程各沿线路段均获得2年的工后沉降监测数据，尚未完成5年内工后沉降的沉降监测，为保障路基的安全稳定，亟需对软土路基沉降进行预测研究．根据施工合同和设计要求，路基5年内工后沉降不超过150mm．

图2 潮汐观测点位置Fig.2 Location of tide observation points

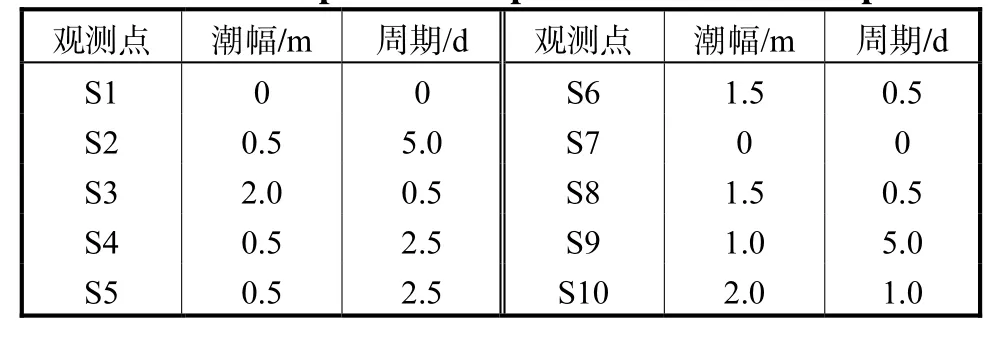
表2 沿线路段各观测点潮幅、周期统计Tab.2 Tidal amplitude and period of observation points

2 数值模型及计算方案

2.1 无潮汐水位下数值模型建立与参数选取

选取无潮汐水位影响的典型工程地质剖面，采用有限元软件PLAXIS2D进行计算分析，模型选择“平面应变”模型．路面宽度为10m，路基平均填方高度为6m，地基尺寸为100m×15m，坡度为1∶1.5，模型如图3所示．

图3 无潮汐水位下路基模型Fig.3 Subgrade model without tidal level

路堤施工前采用塑料排水板联合堆载预压对软土地基进行加固处理，排水板打设深度为9.8m．为了弥补有限元软件进行塑料排水板简化分析的局限性，提高计算效率，本文结合Chai等[20]提出的等效渗透系数方法对塑料排水板处理区进行等效分析，如式(1)和式(2)所示，相关简化模型计算数据见表3．

表3 简化模型计算数据Tab.3 Simplified model calculation data

式中：kve为等效竖向渗透系数；l为塑料排水板打设深度；De为单井等效范围直径；kh和kv分别为水平渗透系数和竖向渗透系数；ks为涂抹区土的渗透系数；qw为塑料排水板的通水性能；井径比n＝De/dw；涂抹比s＝ds/dw，ds为涂抹区直径，dw为塑料排水板等效直径．

地层中粉质黏土、砂土和路堤采用“土体硬化”本构模型，可模拟土体在主压缩条件下的不可逆压缩变形，并可以考虑土体刚度的应力相关性，属于二阶的双曲线弹塑性本构模型．淤泥采用“软土蠕变”本构模型，可反映高压缩性软土的黏性效应，即蠕变和应力松弛．该本构模型基本参数包括修正膨胀指数κ*、修正压缩指数λ*和修正蠕变指数其计算公式如式(3)～式(5)所示．

式中：e为孔隙比；Cr为膨胀指数；νur为卸载-再加载泊松比；Cc为压缩指数；Ca为次固结系数．结合Lei等[22]研究结果，次固结系数Ca约为0.00921，修正蠕变指数为0.004．结合室内三轴试验和现场勘查试验结果，土层材料参数取值如表4所示．

表4 土层材料参数Tab.4 Material properties of the soil

模型位移边界条件：约束模型xmin和xmax水平向位移竖向自由，ymin水平向和竖向均固定，地基和路堤表面自由；渗流边界条件：模型xmin、xmax和ymin均设置为不排水边界，ymax设置为排水边界，即水可通过模型上边界自由排出．为了考虑路基长期沉降规律，数值模拟方案为：①初始地应力平衡；②蠕变分析，计算类型采用“渗流与变形完全吻合”(流固耦合)．该分析基于比奥固结理论，孔隙水压力随时间消散的同时计算有效应力改变引起的土体变形．需要说明的是本文沉降预测结果集中在模拟步骤②阶段，即工后沉降预测．

2.2 监测数据与模型预测结果对比分析

对比分析了路基中心O点、背水面一侧路肩B点沉降及距离背水面一侧坡脚5m位置D1点水平位移监测数据和模型预测结果差异共3方面内容以说明模型参数的正确性，结果如图4和表5所示．从图4可以看出，模型预测结果和监测数据误差在0～1年内均达到最大值，在1～2年内随时间的增加其误差整体上呈现逐渐减小的趋势．从图4和表5可以看出，O点在第0.5年的沉降监测结果与模型预测结果误差最大，为12.55%，B点在第0.75年左右沉降监测结果与模型预测结果误差最大，为10.81%，D1点在第0.3年左右水平位移监测结果与模型预测结果误差最大，为13.67%．但在2年末，监测结果与模型预测结果误差均在0.04%～7.10%，监测结果和模型预测结果具有较好的一致性，满足工程误差控制在15%以内的要求，验证了模型的有效性．

时域自适应滤波抗干扰能够较好地抑制平稳的窄带干扰信号，但是如果干扰信号是时变的，由于存在收敛时间问题，其性能就会大大降低。由于频域滤波抗干扰具有收敛时间短、设计简单直接等优点，因此，我们引入了将频域与时域相结合的抗干扰技术[6]。

图4 模型预测结果与监测数据曲线Fig.4 Curves of prediction results and monitoring data of model

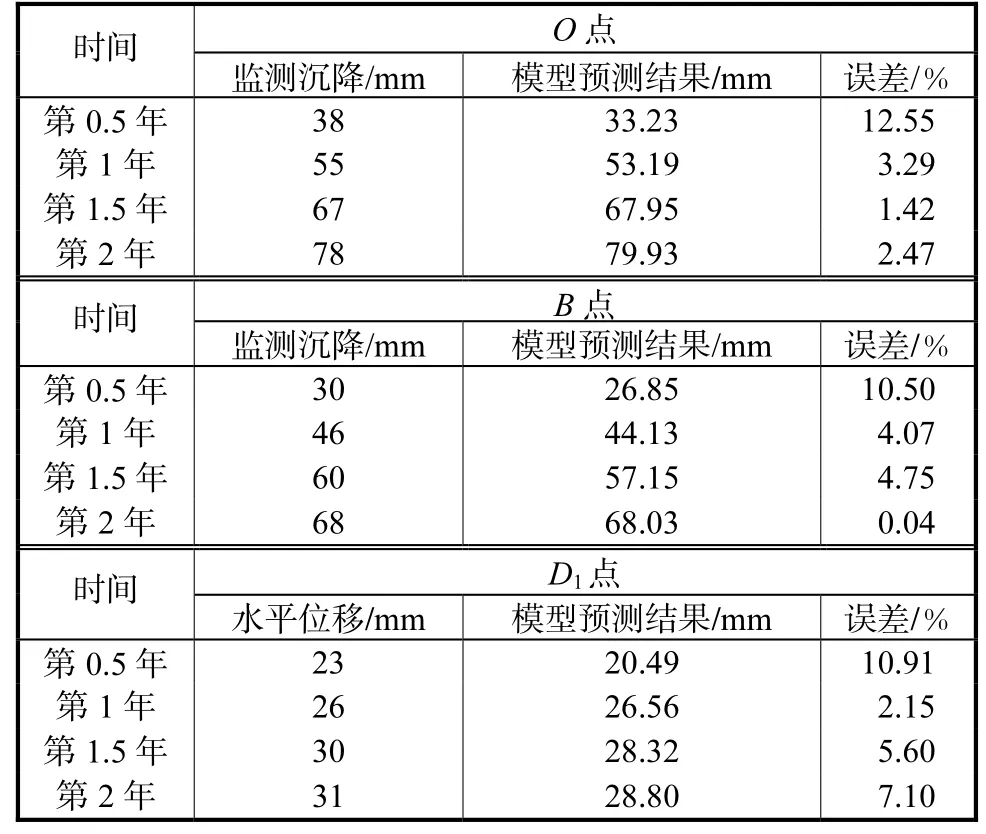
表5 预测结果与监测数据误差Tab.5 Error between prediction results and monitoring data

2.3 考虑潮幅和周期影响因素的数值模拟方案

考虑潮幅和周期的路基模型尺寸、本构模型和土体参数选取与无潮汐水位下路基模型基本一致，仅需根据实际情况设置渗流边界条件，在路基迎水面一侧添加潮汐水位流函数，路基背水面一侧水位保持地下水位不变，潮汐水位下路基模型如图5所示．根据潮汐变化规律将潮汐水位简化为余弦函数施加在路基迎水面一侧，作用时间为5年(1825d)，见图6．

图5 潮汐水位下路基模型Fig.5 Subgrade model under tidal level

图6 潮汐水位变化Fig.6 Tidal water level changes

结合工程实践中水位潮幅(0.5m～2.0m)和水位周期(0.5d～2.5d)变化范围，提出16种模拟工况，如表6所示．

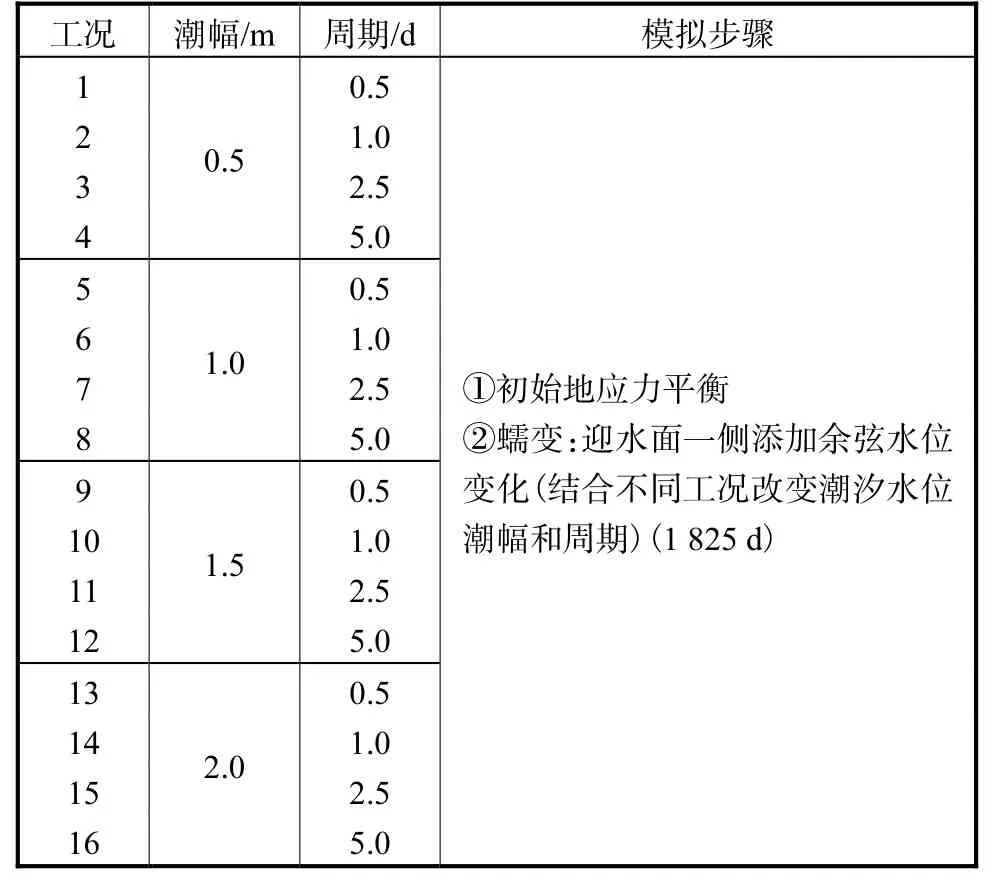
表6 模拟工况Tab.6 Simulation working conditions

3 数值模拟结果分析

3.1 路基沉降规律

图7为不同潮幅沉降和沉降速率随时间变化曲线．从图中可以看出，O点沉降随时间增加逐渐增大，沉降速率随时间增加而逐渐减小，呈现两阶段变化．初始阶段沉降较大，沉降速率范围为0.09～0.57mm/d，后期沉降逐渐趋于稳定，沉降速率范围为0.06～0.09mm/d．同一周期O点沉降随潮幅的增大而增大，在第5年末不同潮幅沉降分别为116mm、127mm、142mm、161mm，无潮汐水位下O点沉降为107mm，增加范围为9～54mm．

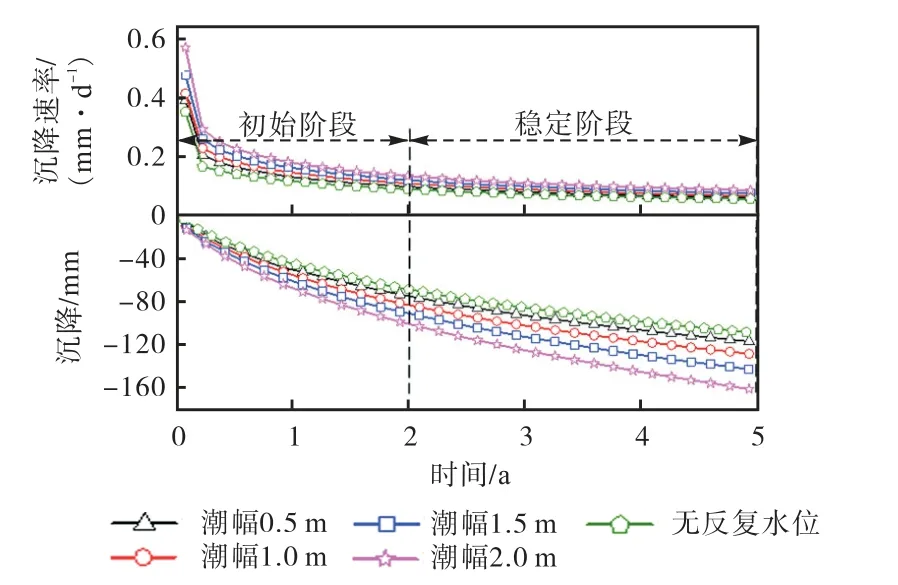
图7 不同潮幅沉降和沉降速率随时间变化曲线Fig.7 Curves of settlement and settlement rate with time under different tidal amplitudes

图8为不同周期沉降和沉降速率随时间变化曲线．从图中可以看出，O点沉降在周期0.5～1.0d内随周期增大而增大，在周期1.0～5.0d内随周期增大而减小，沉降随周期增大总体呈现先增大后减小的趋势，存在临界周期为1.0d时沉降最大，在第5年末不同周期沉降分别为127mm、131mm、129mm、125mm，对比无潮汐水位下O点沉降增加范围为18～24mm．同一潮幅不同周期沉降速率随时间变化不明显，同样呈现两阶段变化，初始阶段沉降速率范围为0.12～0.42mm/d，稳定阶段沉降速率范围为0.07～0.12mm/d．

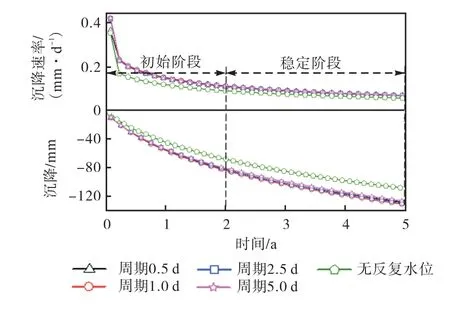
图8 不同周期沉降和沉降速率随时间变化曲线Fig.8 Curves of settlement and settlement rate with time under different tidal periods

3.2 路基水平位移分析

图9为不同潮幅坡脚两侧C、D点水平位移随时间变化曲线．从图中可以看出，在潮汐水位作用下，潮幅的增加增大了路基坡脚C点向迎水面一侧的水平位移，且潮幅越大，水平位移增加速率越快，在第5年末不同潮幅水平位移分别为13mm、39mm、69mm、99mm．相较于无潮汐水位，坡脚D点水平位移在潮幅0.5～1.0m内随潮幅增大其水平位移变化不明显，潮幅1.0～2.0m内随潮幅增大向路基背水面一侧的水平位移急剧增加，第5年末不同潮幅水平位移增加值分别为57mm、65mm、87mm、120mm．

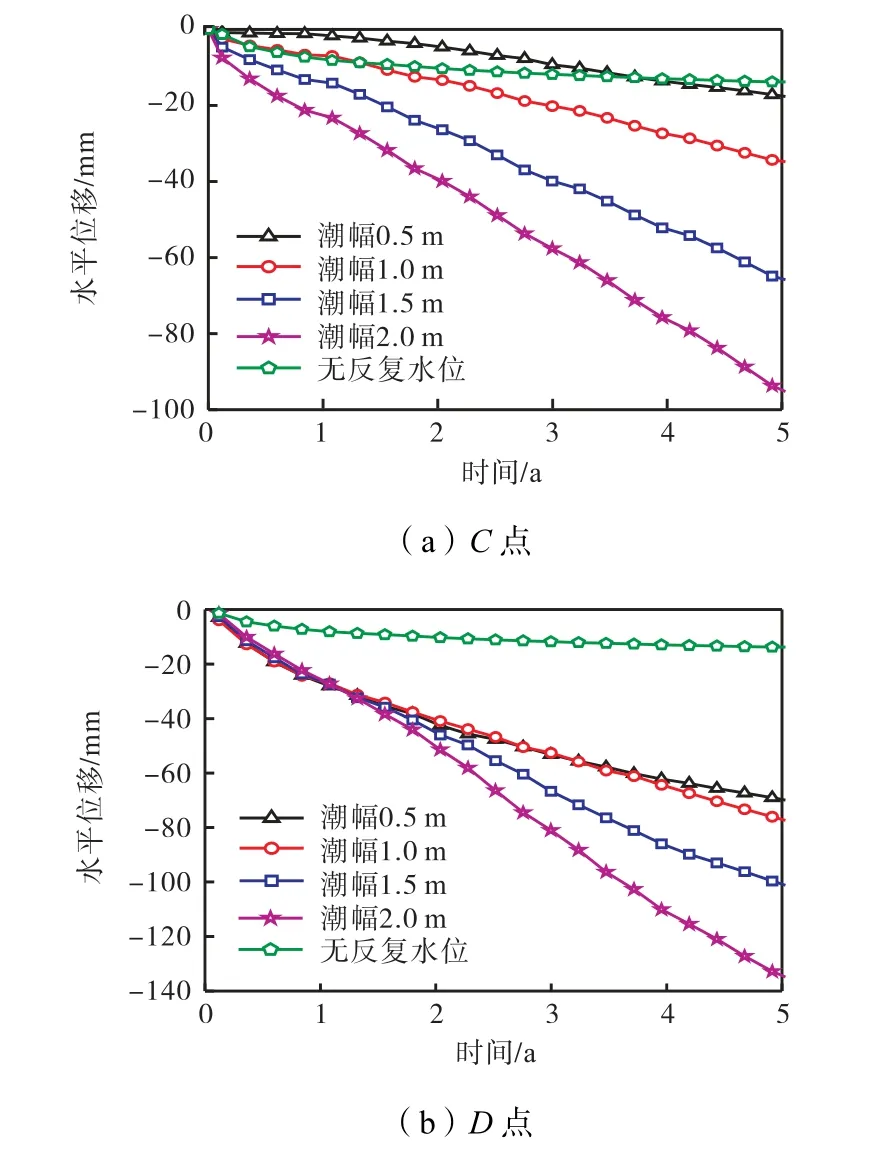
图9 不同潮幅C、D点水平位移随时间变化曲线Fig.9 Curves of the horizontal displacement of points C and D under different tidal amplitudes

图10为不同周期水平位移随时间变化关系曲线．从图中可以看出，坡脚C点水平位移随周期增大呈现先增大后减小的趋势，在周期为1.0d时水平位移最大，第5年末不同周期水平位移分别达到94mm、101mm、79mm、65mm．与无潮汐水位相比，坡脚D点在周期0.5d～1.0d内其水平位移明显增加，在周期为0.5d时其水平位移最大，周期2.5d～5.0d内随周期增大其水平位移逐渐趋于稳定，第5年末不同周期水平位移增加值分别为57mm、59mm、72mm、94mm．

图10 不同周期C、D点水平位移随时间变化曲线Fig.10 Curves of the horizontal displacement of points C and D under different tidal periods

3.3 路基剖面沉降差异规律分析

图11为不同潮幅路基剖面沉降差异与位置关系曲线，图中沉降差异是指路基剖面任意位置处沉降量与迎水面一侧坡脚C点的沉降量的差值．从图中可以看出，沉降差异沿路基位置从左至右先增大后减小，呈现出“U”形发展模式；最大沉降差异位置随潮幅增大逐渐向路基迎水面一侧移动；随着潮幅的增大，背水面一侧坡脚D点的沉降差异逐渐减小；潮幅0.5～2.0m内最大沉降差异分别为97mm、103mm、116mm、136mm，相比与无潮汐水位下路基剖面最大沉降差异增加值分别为2mm、8mm、21mm、41mm．

图11 不同潮幅路基剖面沉降差异与位置关系曲线Fig.11 Curves between the settlement difference and location of the subgrade under different tidal amplitudes

图12 不同周期路基剖面沉降差异与位置关系曲线Fig.12 Curves between the settlement difference and location of the subgrade under different tidal periods

4 潮汐水位下路基长期沉降预测研究

4.1 沉降预测公式建立

对比分析了分层总和法、Terzaghi固结理论、双曲线拟合法和灰色预测法对无潮汐水位下路基中心沉降预测值与监测数据的差异，结果如图13所示．各沉降计算方法相关参数取值如表7所示．

图13 沉降计算方法结果对比Fig.13 Results obtained using different settlement calculation methods

表7 沉降计算方法参数取值Tab.7 Parameter selection for different settlement calculation methods

从图13可以看出，预测误差大小顺序为：分层总和法(规范法)＞Terzaghi固结理论＞灰色预测法＞双曲线法，双曲线拟合方法拟合精度最高，其相关系数R2高达0.99．由于双曲线预测公式无法反映潮幅和周期对路基沉降的影响，本文对其公式进行修正，已知双曲线法的表达式[23]为

式中：St为t时刻累积沉降量；S0为初始时刻沉降；t0为初始时间；α、β为模型待定参数．

从式(6)中可以看出，当t→∞时，S∞→1/β，由于β的取值很小，为提高拟合公式的准确性，选取1/β的值对16种工况按照双曲线法的函数形式进行拟合，结果如表8所示，通过表8可以得到潮幅A、周期T与参数α和1/β关系如图14～图16所示．

表8 双曲线公式拟合结果Tab.8 Hyperbolic formula fitting results

图14为潮幅A与参数α拟合结果，从图中可以看出，参数α随周期T变化幅度很小，相对于参数β对沉降的影响可以忽略，可近似认为参数α仅与潮幅A有关，其关系可以用一次函数来表示，参数α拟合结果位于(-0.734A＋5.08)～(-0.734A＋5.27)区间范围内，取拟合精度最高R2＝0.991的拟合结果作为潮幅A与参数α的拟合关系表达式．

图14 潮幅A与参数α 拟合结果Fig.14 Fitting result of the tidal amplitude A and parameter α

为增加拟合结果的准确性，补充计算当周期为0.25d，潮幅分别为0.5m、1.0m、1.5m、2.0m 4种工况下的沉降数据，结果如图15所示．从图中可以看出，在周期T小于1d时，周期T与参数1/β关系可以用二次函数表示，在周期T为1～5d时用以e为底的对数函数来表示，通过构造分段函数表达式如式(7)所示，且满足a＋b＋c＝m．

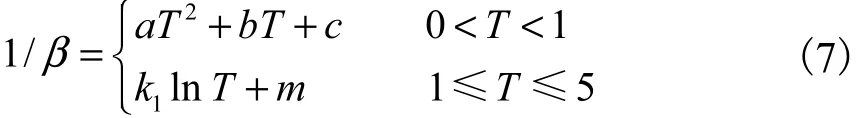
根据拟合结果化简得到

图15给出了周期T与参数1/β拟合结果，从图15中可以看出其拟合结果相关系数R2可达0.761以上，满足精度要求，参数拟合结果见表9．为了建立潮幅A与参数m之间的关系，采用如式(9)函数形式进行拟合，结果如图16所示，相关系数R2可达0.968．

图16 潮幅A与参数m拟合结果Fig.16 Fitting result of the tidal amplitude A and parameter m

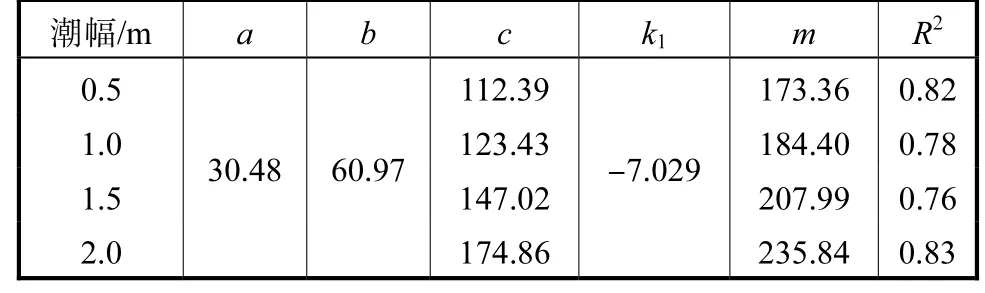
表9 参数拟合结果Tab.9 Parameter fitting results

图15 周期T与参数1/β 拟合结果Fig.15 Fitting result of the tidal period T and parameter 1/β

式中d为模型间接参数．

结合式(6)～(9)提出综合考虑潮幅A和周期T两个参数的沉降预测公式为

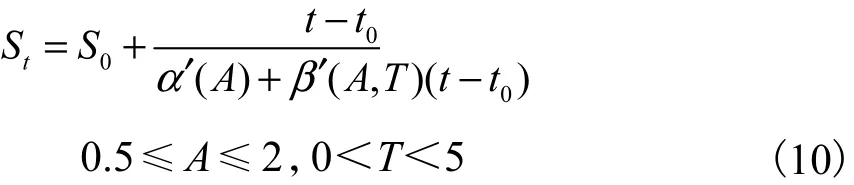
且α′(A)，β′(A，T)满足以下关系式：

4.2 公式验证

基于工程实际选取潮幅2m、周期1d验证公式的预测结果．图17为沉降监测数据与公式计算结果对比，从图中可以看出，第0.5年的沉降计算值和实测值误差最大，实测沉降45mm，计算值为40.6mm，误差达9.78%．第2年沉降计算值和实测值误差最小，为1.39%(见表10)，主要是因为预测公式为双曲线函数，无法反应沉降在初始时刻的快速衰减规律，但可以保证公式计算结果与沉降监测数据的误差控制在15%以内，满足工程计算要求．

图17 沉降监测数据与公式计算结果对比Fig.17 Comparison of the monitoring settlement and formula calculation result

表11为5年内沉降预测值，从表中可以看出，路基在第4.5年时的沉降预测值将超过150mm(不满足施工合同和设计要求)，建议提前采取减小长期沉降的控制措施．

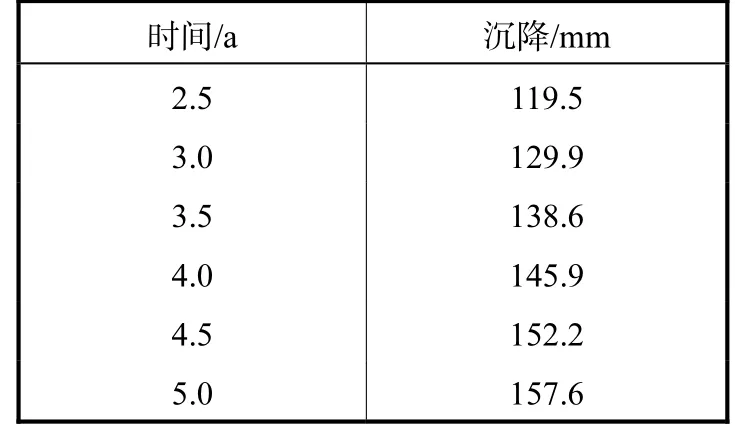
表11 工程5年内沉降预测值Tab.11 Prediction of the settlement of the project in 5 years

4.3 MATLAB-GUI沉降计算程序研发

为了实现潮汐水位下路基沉降的快速计算并应用于工程实践，基于提出的考虑潮幅和周期影响因素的路基长期沉降预测公式，利用MATLAB软件提供的用户可视化交互式工具 GUI(graphical user interface)，研发了潮汐水位下软土路基长期沉降计算程序．

该程序界面如图18所示，通过选取3个Edit Text控件，用于输入潮幅和周期以及输出最终沉降量的计算结果，选择两个Push Button控件，其String属性分别为“计算/导出数据”和“退出”，插入一个Axes坐标轴控件用于绘制时间-沉降曲线并输出相应的数据文件．程序增加Menu Bar菜单栏，分别为“文件”、“编辑”、“工具”、“帮助”，用于快速对绘制曲线进行“保存”、“另存为”、“复制图像”、“导入实测数据”等操作，Context Menus菜单方便用户在图像显示区域右击鼠标实现对沉降曲线“颜色”和“线宽”的更改．

图18 长期沉降计算程序示意Fig.18 Schematic diagram of the long-term settlement calculation program

为了验证沉降计算程序的准确性和实用性，将16种工况对应的不同潮幅和周期输入到编写的计算程序中，获得了相应的时间-沉降数据并与数值模拟结果进行对比得到误差汇总如表12所示．从表中可以看出，误差最大为6.65%，满足工程要求．此外程序新增加沉降监测数据输入接口，方便对程序计算和现场实测沉降结果进行快速对比，可以为滩涂区类似工程的施工决策提供数据参考．