高海拔复杂艰险山区铁路隧道在火灾场景下的行人疏散仿真

李 聪，孙会君，薄 颖，任玥璇，康柳江

（1.北京交通大学 交通运输学院，北京 100044；2.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081)

0 引言

随着我国铁路路网逐渐向西部山区扩展，高海拔隧道工程得到前所未有的发展，而隧道防火安全是贯穿工程项目设计、施工和运营的关键问题。尤其在隧道施工期间，一旦发生火灾，将造成较大的人员伤亡、经济损失和环境污染，不仅延误工期，而且对隧道结构造成损坏。针对隧道火灾，国家出台了《铁路隧道防灾救援疏散工程设计规范》《建筑防火设计规范》《铁路工程施工安全技术规程》等规范标准[1-3]，但这些技术成果都是基于平原隧道的火灾研究所得。

受高海拔地区特殊的气候环境和复杂的地形条件影响，火灾燃烧的特性和烟气扩散规律不同于低海拔地区。陈汉波[4]发现与平原隧道相比，高海拔隧道火源点处的最高温度高，但远离起火点区域的温度低，且火灾稳定阶段的烟气扩散速度快。陈绍华[5]提出在高海拔隧道内采用均衡分散式竖井排烟技术可以控制烟气的扩散和下沉。王明年等[6]研究了高海拔大纵坡铁路隧道的火灾特性，发现大纵坡能够抑制烟气往火灾上游扩散。

隧道施工期间的火灾危险程度与整个隧道运营期间的危险程度不同。施工隧道一端封闭的狭长空间结构会打断烟气的分层规律，使得烟气提前充满整个隧道。同时，人们对疏散通道、排烟方案和消防设施的选择也各不相同。加之高海拔地区低温、低压、低氧、强紫外线的自然环境，导致机械设备的工作效率下降、污染物排放增多。在这些不利因素的影响下，施工人员的活动范围和运动能力受到限制。因此，研究高海拔隧道施工过程中的火灾特征及人员疏散能力，对隧道消防和人员疏散管理具有重要意义。

国内外学者常采用微观模型描述行人疏散特征和运动规律，典型代表有社会力模型、元胞自动机模型、智能体(Agent)模型等[7]。随着计算机技术的发展，计算机仿真人群疏散得到越来越多学者的关注，主要的行人交通仿真软件有AnyLogic，Legion，STEPS，EXODUS 等30 多种，国际上比较权威的紧急疏散建模方式都可以用AnyLogic 实现[8]，因而研究采用AnyLogic 软件对行人疏散仿真建模。

研究将利用火灾模拟软件模拟在高海拔施工隧道环境下的火灾动态发展，获得监测点烟气、温度、CO 浓度的时空分布数据。为了使行人速度随火灾产物动态变化，利用火灾产物对疏散速度的影响公式，计算疏散速度综合折减系数，修正社会力模型中行人期望速度，模拟行人在火灾场景下的疏散速度及疏散人数随时间的变化情况。

1 高海拔施工隧道FDS 火灾数值模型建立

以海拔3 500 m、坡度0°的主洞作为研究对象，采用火灾动力学模型(FDS)建立施工隧道火灾模型。马召辉[9]在研究高海拔特长隧道烟气蔓延规律时，建立的单洞单线铁路隧道模型长和宽都为10 m，考虑到普通旅客列车宽3.1 m，高4.1 m，因而研究将隧道横截面的半径设为5 m。由于模型为在建隧道，长度仅表示施工距离，考虑到火灾模拟时间为420 s，行人在火灾条件下的平均速度约0.7 m/s，所以取隧道长度为300 m。隧道三维模型示意图如图1 所示，隧道长300 m，宽10 m，拱顶高5 m。假设隧道一端封闭，忽略平行导洞，当掌子面发生火灾，火灾规模20 MW，火源尺寸2 m×2 m，无机械通风条件下，模拟隧道火灾、烟气自然发展情况。

图1 隧道三维模型示意图Fig.1 3D model of tunnel

为方便观察火灾产物和人员疏散的空间分布，沿隧道中轴线按100 m 等间隔划分为A 区、B 区、C 区，起火点与监测设备示意图如图2 所示。监测器可测得不同地点的温度、能见度以及CO 浓度的数值变化，考虑到距离起火点越近，火灾产物的变化幅度越明显，故监测器的设置在A 区每10 m一个，在B 区与C 区每50 m 一个，沿隧道中轴线排列，特征高度设置为2 m。

图2 起火点与监测设备示意图Fig.2 Fire point and monitoring equipment

火灾模拟结果的精确程度直接取决于热释放速率。一般情况下，认为火灾的热释放速率随时间的平方呈非线性变化，因而采用t2火灾模型模拟火灾发展，设置火灾增长类型为快速火，火灾增长系数为0.046 9 kW/s2。

网格是用来记录火灾模拟数据的最小单位。由火灾直径计算公式[10]可知，每平方米热释放速率为5 000 kW 的火焰在3 500 m 海拔下，火焰高度约2.5 m。一般情况下，网格尺寸为火焰高度的1/16～ 1/4。因此，网格尺寸在[0.15 m，0.625 m]范围内即可，研究设置网格尺寸为0.5 m×0.5 m×0.5 m，整个模型共计120 000 个网格。

不同海拔高度下的环境参数不同，对火灾特性的影响也不同。综合考虑高海拔特殊的气候条件，如大气压强、氧含量、温度、空气密度、重力加速度、相对湿度等对火灾的影响，设置不同海拔高度的环境参数对比如表1 所示。

表1 不同海拔高度的环境参数对比Tab.1 Comparison of environmental parameters at different altitudes

2 人员疏散模型

2.1 社会力模型

社会力模型是Helbing 等[11]提出的连续型微观仿真模型，该模型以牛顿力学为基础，通过自驱动力、行人之间的相互作用力，以及行人与障碍物之间的排斥力来描述行人在复杂环境中的运动过程。社会力模型如公式 ⑴、公式 ⑵ 所示。

通过改变社会力模型中的参数或添加其他影响因子，可以实现模拟不同灾害场景下的仿真效果。研究在社会力模型的基础上，通过改变行人期望速度改变自驱动力，使行人运动速度受火灾产物影响。

2.2 火灾产物对疏散速度的影响

在真实火场环境下，人员疏散速度和疏散方向受到火灾产物的影响，会出现疏散速度降低、无法辨别方向等现象。根据现有研究[12]，火灾条件下行人疏散速度如公式 ⑶、公式 ⑷ 所示。

式中：v表示当前速度，m/s；v0表示人员初始速度，m/s；σ表示疏散速度综合折减系数；f1(ks)表示能见度影响系数；f2(ρ)表示CO 浓度影响系数；f3(Ts)表示烟气温度影响系数。

（1）能见度影响系数。能见度是指人眼在大气中所能观察到的最远距离，假设正常情况下人眼特征高度处的能见度为30 m。为使人员危险程度与影响因素呈正相关分布，引入减光系数的概念，减光系数与能见度成反比，与人员危险成正比。在建筑火灾中常用的减光系数与能见度的换算如公式 ⑸所示，能见度影响系数计算如公式 ⑹[13]所示。

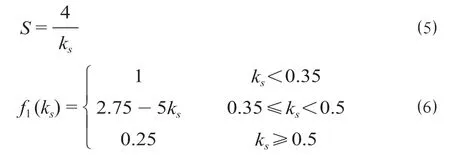
式中：S为能见度，m；ks表示减光系数，m-1。

（2）CO 浓度影响系数。CO 浓度影响系数计算如公式 ⑺ 所示。

式中：ρ表示CO 体积分数，%；t为暴露时间，min。

（3）环境温度影响系数。美国学者Milke 通过研究环境温度与乘客行走速度的数据，得出不同温度范围内温度对乘客速度的影响系数[14]，如公式 ⑻ 所示。

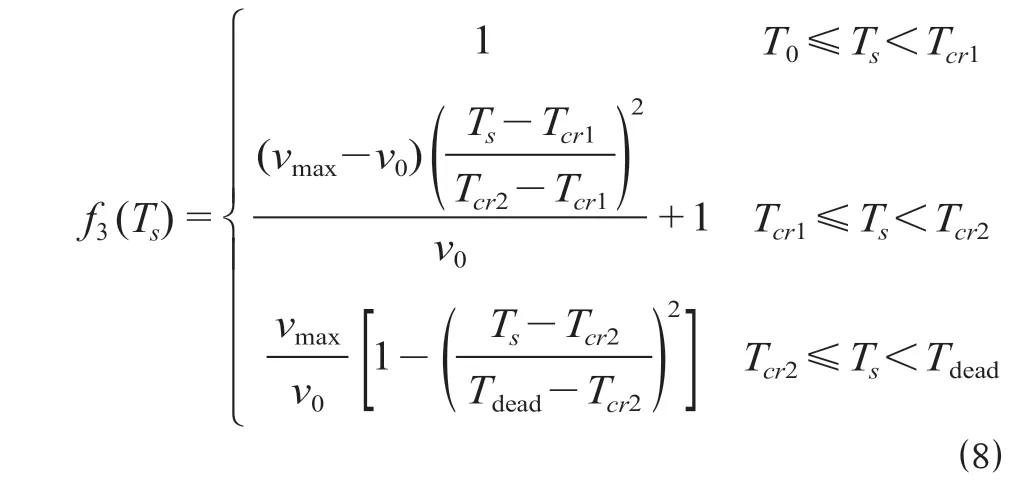
式中：Ts表示火场温度，℃；v0表示人员初始速度，m/s，取1 m/s；vmax表示最大逃生速度，m/s，取1.27 m/s；Tcr1表示人员感到不适的温度，取30 ℃；Tcr2表示对人员造成伤害的温度，取60 ℃；Tdead表示致死温度，取120 ℃。

2.3 行人疏散仿真建模

假设在同一尺寸的隧道模型中随机分布100 名施工人员，紧急出口只有洞口一个。模型启动时行人开始疏散，当行人速度衰减为0，表示疏散失败。

考虑到高原缺氧和寒冷环境的影响，人员疏散速度会随海拔高度上升出现折减。根据调查，平原地区青壮年男性的紧急疏散速度约2.0～ 2.5 m/s，而高海拔地区施工人员的劳动能力比平原降低40%～ 50%，跑步能力下降75%～ 80%[15]。因此，研究设置行人初始疏散速度服从1.5～ 2 m/s 的均匀分布。

为了完成火灾影响下行人速度设置，将仿真时间按1 s 等间隔划分为420 个阶段，同时按照火灾监测器布局，将隧道空间沿纵向划分为14 个区域，空间划分如图3 所示。根据疏散速度影响公式分别计算得到各阶段火灾产物监测器所在位置的影响系数，并在AnyLogic 中使用420×14 的二维数组存储。

图3 空间划分Fig.3 Space division

3 仿真结果分析

根据《铁路隧道防灾救援疏散工程设计规范》[1](以下简称《设计规范》)规定，隧道内特征高度2 m 处的温度超过60 ℃、能见度低于10 m (减光系数大于0.41 m-1)、CO 浓度超过400 ppm[9]，以上任意一项指标超过临界值，都会对人员造成致命伤害。

3.1 温度

不同地点温度随时间变化曲线如图4所示。图4展示了特征高度2 m 处不同地点温度随时间的变化。由图4 可知，仿真时间内，隧道内最高温度约45 ℃，明显低于《设计规范》中要求的临界值。因此，温度对作业人员的生命安全暂未构成威胁。

图4 不同地点温度随时间变化曲线Fig.4 Curves of temperature variation with time at different locations

3.2 能见度

不同地点能见度随时间变化曲线如图5 所示。图5 展示了特征高度2 m 处不同地点能见度随时间的变化。假设正常情况下能见度为30 m，由图5可知，距离起火点约100 m 处，能见度最先到达临界值。在起火点100 m 范围内，距离起火点越远，能见度从开始变化到达到临界值的时间越短。火灾发生100 s 后，特征高度2 m 处的能见度才出现明显变化。

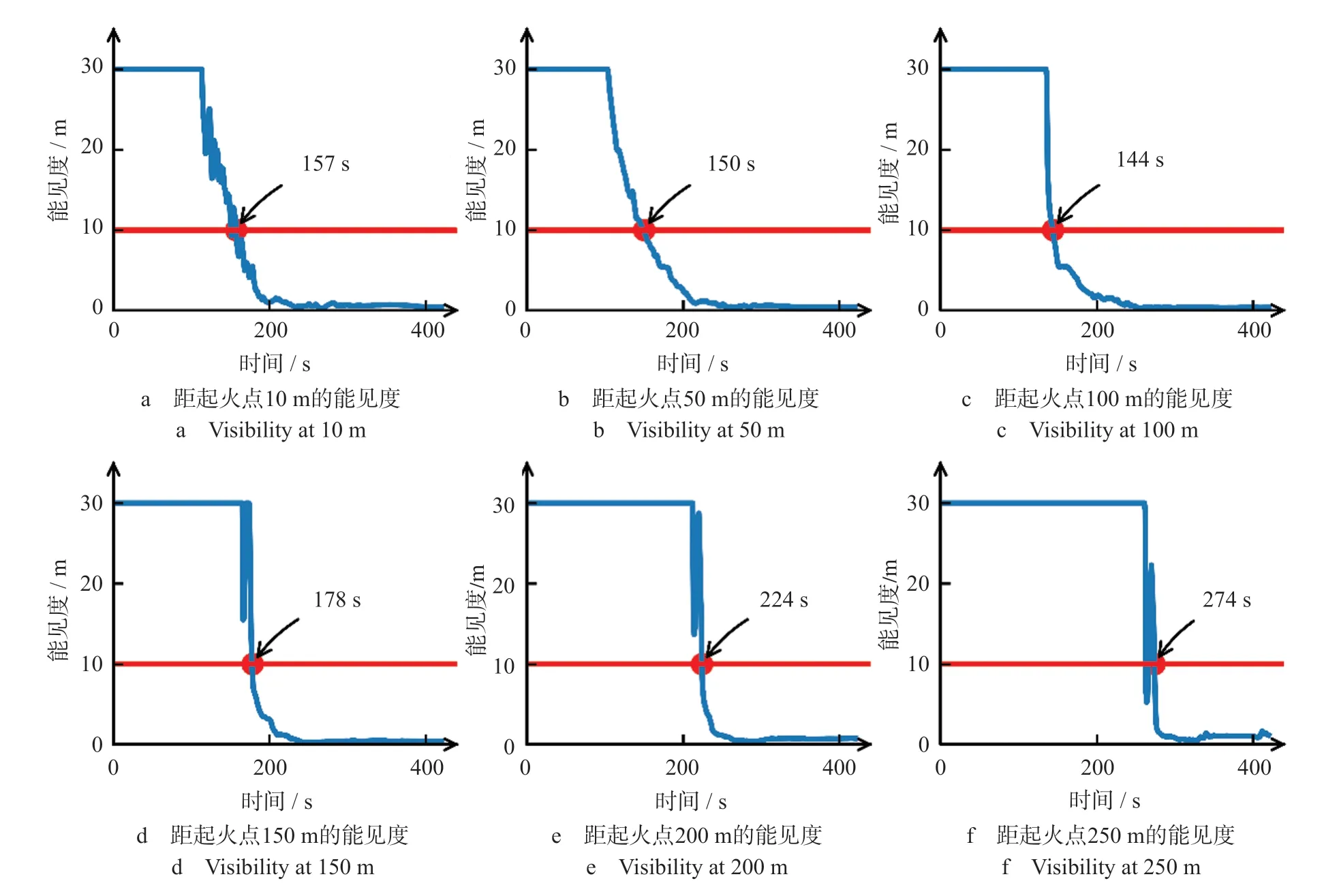
图5 不同地点能见度随时间变化曲线Fig.5 Curves of visibility variation with time at different locations

3.3 CO 浓度

不同地点CO 浓度随时间变化曲线如图6 所示。图6 展示了特征高度2 m 处不同地点CO 浓度随时间的变化。由图6 可知，CO 浓度变化不稳定，时高时低呈锯齿形增长，原因是CO 密度比空气小，容易受到其他气流的干扰。因此，制定合理的通风排烟方案可以阻碍CO 扩散，为行人疏散争取宝贵时间。图6 显示，距离起火点越近，CO 所能达到的浓度越高，洞口附近虽然通风条件好，利于稀释CO 浓度，但整体来看，CO 浓度始终处于较高水平。

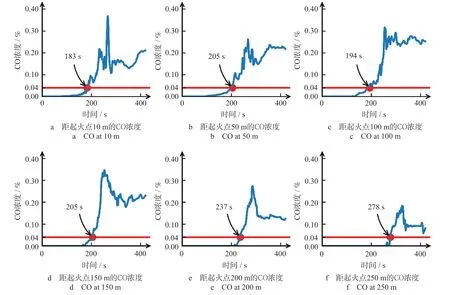
图6 不同地点CO 浓度随时间变化曲线Fig.6 Curves of CO concentration variation with time at different locations

3.4 烟气蔓延

烟气蔓延示意图如图7 所示。图7 展示了30 s，60 s，90 s，120 s 时刻的烟气蔓延情况，结合上述火灾产物随时间的变化规律可知，火灾发生100 s后，特征高度2 m 处的能见度和CO 浓度才出现明显变化，而此时烟气已扩散80 m 左右。因此，火灾发生初期，烟气以上升和纵向扩散为主，下沉现象不明显。

图7 烟气蔓延示意图Fig.7 Smoke spread

3.5 可用安全疏散时间

结合火灾模拟数值分别确定14 个监测点温度、能见度和CO 浓度到达临界值的时间，取这些时间的最小值，得到各个监测点的可用安全疏散时间。不同地点的可用安全疏散时间如图8 所示。由图8可知，能见度最先到达临界值，虽不能对人体造成直接损害，但制约行人的疏散速度。CO 浓度超标是造成人员伤亡的主要原因。火灾发生后的150 s 之内，人员能够迅速逃生是相对安全的。隧道中间区域的可用安全疏散时间最短。原因是在热气压带动下，烟气蔓延速度加快，同时受烟囱效应影响，烟气纵向扩散一段距离后，开始出现沉降。采用二次曲线拟合，相关系数R2等于0.992，表示模型具有参考价值。

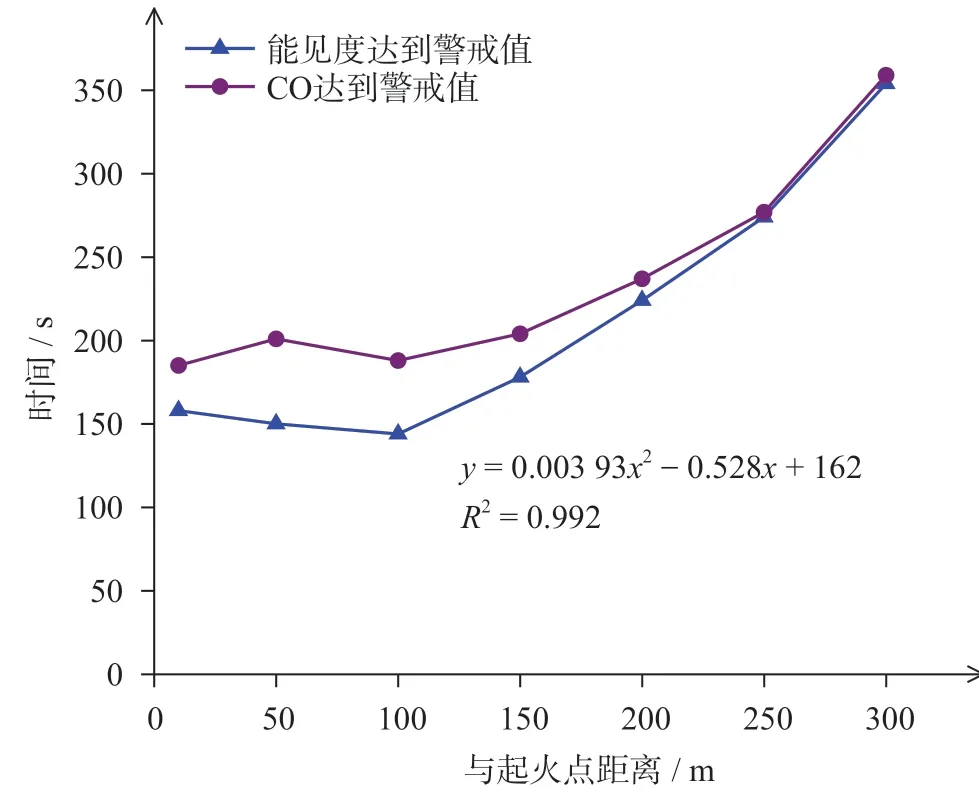
图8 不同地点的可用安全疏散时间Fig.8 Available safe evacuation time at different locations

3.6 不同响应时间下的疏散情况

在真实的火场中，探测器和人员对火灾信息的掌握有一定的延迟，为了使仿真效果更加真实，在模型中添加响应时间。不同响应时间下的疏散情况如图9 所示。图9 中，总疏散时间表示起火时刻到人员疏散至安全区域的时间，包含响应时间和人员的疏散时间。当响应时间小于90 s 时，所有人员可以安全疏散，行人平均疏散时间大致相同，总疏散时间随响应时间线性增长。

当响应时间处于90～ 150 s 时，A 区死亡人数增加，平均疏散时间下降，总疏散时间出现明显波动，原因是在火灾产物影响下，行人疏散速度降低，虽然能保证在速度降为0 m/s 前逃出隧道，但使总疏散时间变长。由图9 可知，伤亡人数随响应时间的增加呈阶梯型增长，A 区作业人员最容易受到火灾产物的影响。因此，在火灾风险高的地方应配置足够多的防毒面罩，以保证人员顺利逃生。

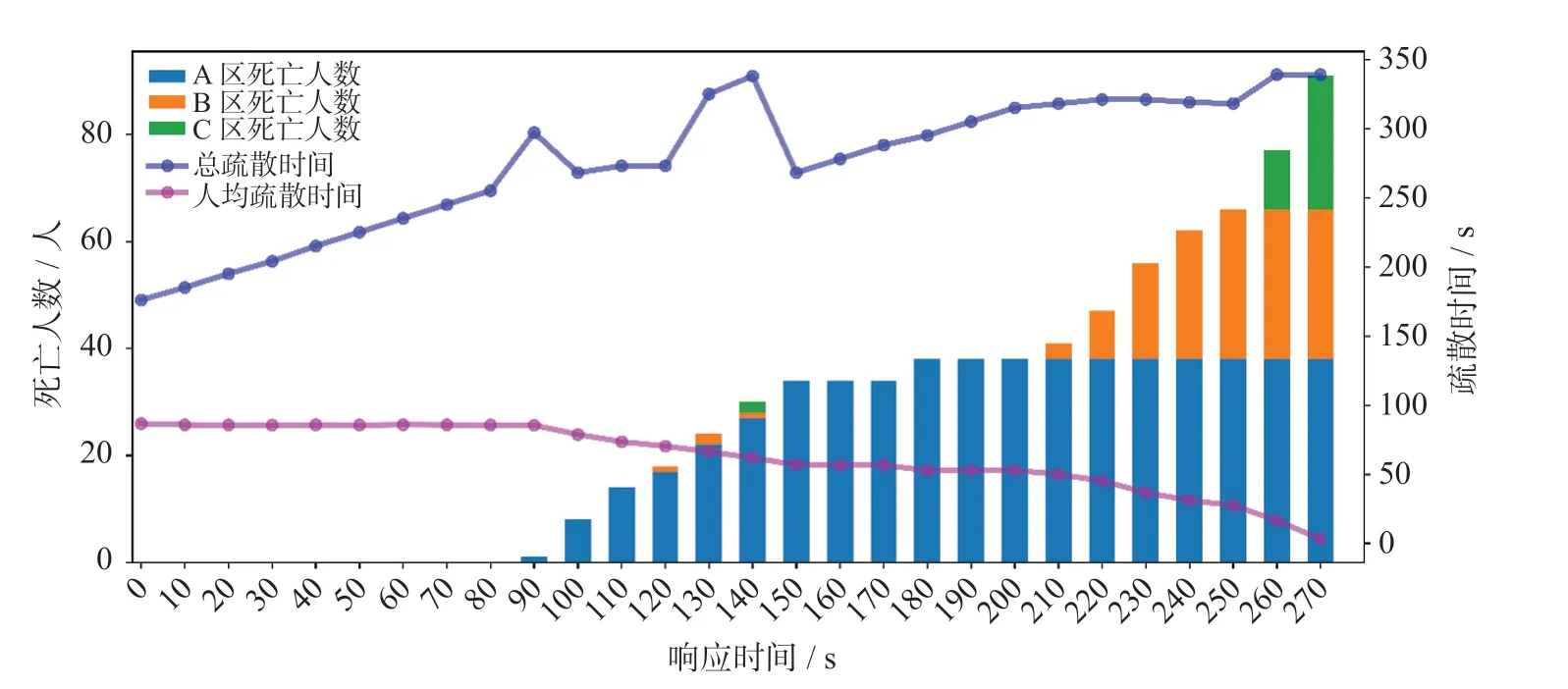
图9 不同响应时间下的疏散情况Fig.9 Evacuation under different response time

4 结论

在高海拔复杂艰险山区修建铁路隧道，不仅要克服低温、低压、低氧、冻土环境带来的施工难题，还要考虑人员运动能力受环境影响等因素。研究通过火灾模拟得到该场景下温度、能见度、CO 浓度随时间的变化规律以及烟气的蔓延情况，结合火灾产物对疏散速度影响公式，研究不同响应时间对总疏散时间和伤亡人数的影响，仿真结果如下。

（1）温度对人员的生命安全暂未构成威胁，起火点附近的烟气扩散以上升和纵向扩散为主，烟气下沉不明显，故火灾报警装置应安装在拱顶位置。

（2）伴随火灾发展，行人体感温度升高，心理压力增大，迫使行人加快疏散速度，综合考虑温度、能见度和CO 浓度等因素可知，火灾发生后的150 s 之内，人员迅速逃生是相对安全的。

（3）伤亡人数随响应时间的增加呈阶梯型增长，火源点附近的伤亡人数最多；CO 浓度在整个仿真时间内都处于较高水平，是造成人员伤亡的主要因素。因此，应在有火灾风险隐患的地方配备足够的防毒面罩。