浅析ETA物理认知模型在中学物理习题教学中的应用*

黄志鹏

(喀什大学教育科学学院 新疆 喀什 844000)

周向玲 郭 亮

(喀什大学物理与电气工程学院 新疆 喀什 844000)

物理习题教学是教师指导学生运用理论解决实际问题的起点[1].习题教学能够帮助学生更好地掌握物理观念和物理原理，用科学的思维观察自然界的现象，养成以科学方法探究问题的习惯，提高学生分析问题、解决问题的能力，形成科学的态度来看待周围的事物，发展学生的物理学科核心素养，其意义和作用不言而喻.

文献[2]将习题教学提升为物理问题解决教学，列举了物理问题解决的形式、作用，重点探讨了物理计算题的解题策略和习题教学的要求和程序.文献[3]主要分析和总结了物理习题教学的规律.文献[4]详细介绍了物理解题的全过程，包括解题步骤、解题策略、解题方法以及影响解题成功的因素.国内对习题教学的研究一般侧重习题解题方法研究.本文尝试基于ETA物理认知模型从认知角度对习题教学进行讨论.教师可以通过不同类型题目的评讲，帮助学生克服从实践到物理模型的跨越困难，完善理论物理认知，发展应用物理认知，最终收获良好的习题教学效果.

1 ETA物理认知模型

物理是一门观察和实验为基础的学科[5]，在探究事物运动规律本质过程中，物理学家运用许多物理方法，通过归纳出简洁的公式对事物的运动规律概括描述，从而构筑完整的物理知识体系，完善物理认知.物理教育就是通过学习，使学生懂得物理的真谛，为我所用.

穆良柱教授通过前人的物理实践探究过程总结归纳出一套物理认知模型[6]，即ETA物理认知模型.ETA物理认知模型是研究物理认知规律的一种模型，该认知模型中的E，T，A分别指实验物理(Experimental Physics)、理论物理(Theoretical Physics)、应用物理(Applying Physics).模型主要包含11个认知步骤，大致分为3个认知阶段.概括为实验物理认知、理论物理认知、应用物理认知，具体如表1所示.

2 ETA物理认知模型在习题教学中的作用

习题教学是物理认知在物理问题上的应用，教师自身需要对物理认知有清楚的认识，拥有完备的理论体系，并且能够从实际问题出发，获得实验物理认知，将其抽象为物理模型进行解题，获得理论物理认知.根据ETA认知模型可以将物理习题大致分为3类题型：

第一类为理论物理认知题型，该题型仅用到理论物理认知，题目本身提供了一个现成的物理模型，只需要用现有的物理概念或原理即可解决问题；

第二类为实验物理认知到理论物理认知题型，与实际生产生活联系密切的问题，首先需要对问题进行分析，获得实验物理认知，再将其抽象为物理模型，实现从实践到物理模型的认识，再运用相关物理原理进行解题；

第三类为应用物理认知题型，在获得足够的理论物理认知后，可以将此理论进行合理外延演绎推理，来解决实际问题.

需要注意，不是每一道习题解决中都涉及实验物理认知、理论物理认知及应用物理认知这3类认知.

2.1 理论物理认知题型的习题教学

对于理论物理认知题型的习题，主要考查学生对物理规律、物理概念、物理公式的熟悉程度.在实际中只要根据题目明示信息利用现有的物理模型演绎推理就可解决实际问题.

【例1】(2017年高考新课标Ⅲ理综卷第14题)2017年4月，我国成功发射的天舟一号货运飞船与天宫二号空间实验室完成了首次交会对接，对接形成的组合体仍沿天宫二号原来的轨道(可视为圆轨道)运行.与天宫二号单独运行时相比，组合体运行的( )

A.周期变大 B.速率变大

C.动能变大 D.向心加速度变大

习题解析：这道题目中提示组合体仍按圆轨道运行，可知组合体受万有引力作用做圆周运动，只需根据万有引力提供向心力的理论物理认知解决本题即可.根据题意，由运动周期

可知周期不变，选项A排除；因为

所以速率也不变，选项B排除；由于组合体的质量大于天宫二号的质量，所以整体上动能增大，选项C正确；根据

轨道半径不变，速率不变，所以向心加速度也不变，排除选项D.

第一种类型题目的特点主要是物理模型已经给出，如本题中直接给出天宫二号和组合体的运动轨道模型，无需学生自己再另外构建或者只需根据题目中已给定的物理规律、定律演绎推理解题.在这类题型的习题教学策略上，教师需要帮助学生构建完善的理论物理认知，虽然部分题型综合度不高，仅考查了某一单元某一部分的知识点，但学生如果对相关知识点不清楚，也会在此类习题解答上遇到不小的困难，所以需要教师不断复习巩固知识点，知识点再小也不能忽略，强化学生基本知识的掌握，为学生以后更深层次的学习夯实基础.

2.2 实验物理认知到理论物理认知题型的习题教学

实验物理认知到理论物理认知是指由实践中复杂的实际问题抽象出物理模型，再利用相关理论知识进行解题.相当多的学生遇到第一类题型解决起来得心应手，游刃有余，然而遇到第二类题型，往往会束手无策，一筹莫展，无法实现从实践认识到物理模型的跨越.本文重点讨论此类题型的习题教学.

【例2】如图1所示运动员持网球拍托球跑.开始加速时运动员用水平力推球拍，问网球拍偏离水平多大角度，网球相对球拍静止[5].

图1 运动员手持球拍图

习题解析：本题立足于生活实际，属于力学的练习题，是典型的从实践到物理模型的习题，归属第二类题型，涉及的相关知识属于高中生的知识体系.根据人托网球的实际情况，利用主次法，抓住人对网球拍的作用、网球拍对球的作用等主要因素，忽略人的手、托球时的体态等次要因素，将其抽象为一定的物理模型.人对网球球拍的力促使球拍向前水平运动，并使得网球拍保持在一个水平面移动不至掉落地面，因此可将人对网球拍的合力根据力的效果分解为竖直方向和水平方向的分力.根据上述分析构建如图2所示的物理模型(斜劈在光滑的地面上，地面对其有向上的支持力，水平外力作用在斜劈上)，在构建物理模型时要注意模型一定要与题中给出的条件严格对等.

图2 球拍与网球物理模型

设网球拍质量为m1，网球质量为m2，如图2建立直角坐标系xOy,网球拍与水平方向的角度为α，然后运用隔离法分别对网球拍与球进行受力分析，如图3和图4所示.其中FN1为球对球拍的压力，FN2为球拍对球的支持力，FN为支撑面弹力.

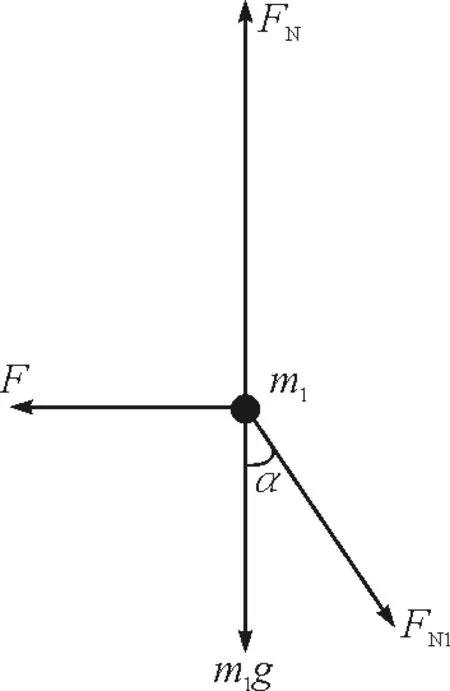
图3 球拍受力示意图

图4 网球受力示意图

根据牛顿第二、三定律，抓住关键词“网球相对球拍静止”可知两者具有相同的加速度，综上，可列出下式.

对于球拍，有

-F+FN1sinα=-m1a

(1)

对于网球，有

-FN2sinα=-m2a

(2)

-m2g+FN2cosα=0

(3)

由式(1)、(2)、(3)解方程得

由上面习题可知，解题的关键点在于实际问题到物理模型的转化.遇到这类复杂的实际问题，学生需紧扣题中关键题点，理解背后隐藏含义.教师在评讲本类型题时可以让学生预先独立思考，认真审题，在构建物理模型过程中，不断提出问题对学生加以引导.在分析实际问题中，找出关键条件后，教师需引导学生将关键条件与物理模型相匹配，不能少一个条件也不能多一个条件.

【例3】(2009年高考理综全国卷Ⅱ第26题)如图5所示，P和Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为ρ；石油密度远小于ρ，可将上述球形区域视为空腔.如果没有这一空腔，则该地区重力加速度(正常值)沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象.已知引力常量为G.

图5 P，Q所在地区石油分布图

(1)设球形空腔体积为V，球心深度为d(远小于地球半径)，PQ=x，求空腔所引起的Q点处的重力加速度反常.

(2)若在水平地面上半径为L的范围内发现：重力加速度反常值在g与kg(k>1)之间变化，且重力加速度反常的最大值出现在半径为L的范围中心，如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积.

习题解析：本题联系具体实际活动探测石油，同样是从实践到物理模型，也属于第二类题型.由题可知若地下有石油，则会出现重力加速度反常，获得实验物理认知.接下来是将实际问题转化为物理模型，根据题中提供的条件，可以构建如图6(a)、(b)所示的模型.

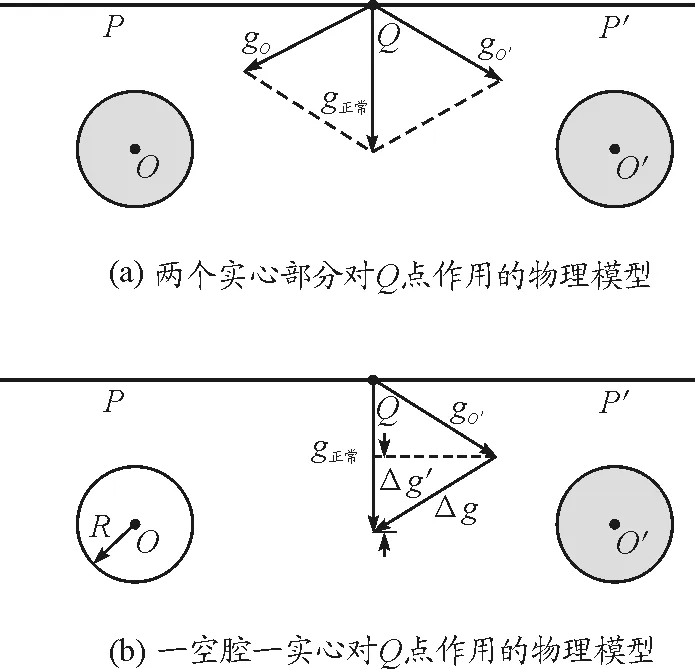
图6 对例3构建模型

根据题中所给条件可将储藏石油的球形区域看作空腔，假设地下没有石油即空腔部分为岩石时，建立如图6(a)所示的物理模型，物体在Q点时的实际重力加速度等效于与O点对称的球形空腔O′与球形空腔O对Q点物体作用的效果.当地下有石油即存在空腔部分，则可建立如图6(b)所示的模型，空腔部分对Q点物体的吸引力消失，只存在球形区域O′对Q点物体的吸引力，则Q点物体所受重力加速度如图(b)表示，Δg为实际重力加速度相对正常重力加速度的偏离，Δg′为Δg在竖直方向上的投影.物理模型构建一定要与题中条件严格等效，构建完模型后可检查一遍是否符合题意.

根据万有引力提供重力，可列出下式

(4)

M=ρV

(5)

r2=x2+d2

(6)

由式(4)、(5)、(6)可得

(7)

又因为

由式(7)可得

(8)

由式(8)可知

(9)

(10)

由式(9)、(10)可得

从以上两题可看出，第二类题型的特点是与日常生活联系密切，没有直接提示物体的运动模型，因此无法直接套用公式定律解题，需要学生思维上转个弯.解决这类题型关键在于将实践抽象为物理模型，认真审题，理解关键词，接下来进行演绎推理便可顺利解题.

教师面对第二类题型时，要对实际问题进行分析，留给学生足够的思考时间进行消化理解，做好从实践到物理模型的过渡，构建过程中条件一定要考虑全面，模型要符合题目要求，这样能促进学生掌握从实验物理认知到理论物理认知的能力，有利于提高学生的科学素质，培养以物理视角看待问题、解决问题的习惯.

2.3 应用物理认知题型的习题教学

基于应用物理认知进行解题，即根据已有的理论体系解题后，并对解题结果结合实践进行讨论或结果进行外延推理，得出新的结论.其结果对实际生活有指导意义.

【例4】(人教版高中物理课本选择性必修二2019版P19第4题)回旋加速器两个D形金属盒分别和一高频交流电源两极相接，两盒放在磁感应强度为B的匀强磁场中，磁场方向垂直于盒底面，粒子源置于盒的圆心附近.若粒子源射出的粒子电荷量为q,质量为m，粒子最大回旋半径为R，求：

(1)粒子在盒内做何种运动；

(2)所加交流电源的频率；

(3)粒子加速后获得的最大动能.

习题分析：本题由已有理论认知体系得出结论并将其应用于生产实践中，属第三类题型.前两问较为简单，着重讨论第(3)问.

根据洛伦兹力提供向心力，同理可得

当磁场与入射粒子确定时，速度与轨道半径成正比

所以最大动能

接下来进行合理外延推理，若要使质量为m，电荷量为q的粒子达到确定速度v0，则需要加多大频率的交流电？在此基础上还可增加条件：设交流电源的电压为U,则可以思考粒子运动了多长时间.

由题中条件得，电场加速粒子的次数为n，依据动能定理，可列

求得

则粒子运动的总时间

通过在一道习题上进行拓展思考，基于理论物理认知外延推理得出新的结论帮助拓宽学生思路，不拘泥于某一道题的解法，养成勤于思考的好习惯.将大大提高学生解决物理实际问题的能力，发展学生的物理学科核心素养.

教师要注重启迪学生做好理论在实际中的应用，鼓励学生进行合理的外延推理，发展学生的发散思维，培养学生的质疑创新精神.

3 结论

运用物理认知模型进行习题教学过程中，可将习题大致分为理论物理认知、从实验物理认知到理论物理认知和应用物理认知3类题型.对第一类题型，教师需要强化基本概念和基本理论知识的掌握；对第二类题型，教师需要留给学生一定的思考时间，做好从实践到物理模型的过渡，构建模型时一定要做好条件类比符合；对第三类题型，教师需要注意启迪学生发散思维，合理外延推理.

3类题型的作用，立足于生活生产实际，能够有效锻炼学生运用理论解决实际问题的能力.第一类题型主要强化巩固学生基础知识，是学生理论联系生活的前提.第二类题型可以培养学生的创新能力.第三类题型有助于学生的创新思维发展.基于ETA物理认知模型对习题教学的分析，为中学物理习题教学提供一定的参考.