带电粒子在匀强磁场中做匀速圆周运动的单元教学思路与框架

李 芳 涂 杰

(广东肇庆中学 广东 肇庆 526060)

单元教学设计是发展核心素养的重要途径，抓住大概念、大思路、大情景与大问题是可行的也是必要的[1].按照科学大概念理念可得出，大概念是有组织、有结构的知识和模型[2].带电粒子在匀强磁场中的运动所涉及的物理知识较少，只有洛伦兹力提供向心力的公式和周期公式，该部分内容一直是高考重点考查对象，且难度较大.经统计近些年有关带电粒子在匀强磁场中运动的文献，以分类解题类居多，也有对带电粒子在磁场中运动的模型进行分类研究[3]，但模型之间缺乏关联，不能形成有组织、有结构的模型.因此在大概念教学理念背景下，对该内容的教学研究非常有意义.

1 教学内容分析

1.1 带电粒子在匀强磁场中运动的特点

(1)忽略重力，带电粒子只受洛伦兹力，且洛伦兹力提供向心力，做匀速圆周运动.

(2)轨迹为圆，任一点切线方向即为速度方向.

(3)带电粒子在磁场中的绕行方向由磁场方向和带电粒子的带电性质共同决定，满足左手定则.

高考考查带电粒子在匀强磁场中做匀速圆周运动的情景一般具有这样的特征：带电粒子会从某点进入匀强磁场，再从另一点射出磁场区，多个组合磁场，周期性变化的磁场等都可以按这个思路去分析.带电粒子的轨迹一般情况下是不完整的圆周，入射点和射出点即轨迹圆周与磁场边界的两个交点，两交点的连线即轨迹圆的一条弦.

1.2 解题基本步骤

确定圆心、半径、画轨迹.通常用两种方法确定圆心位置：过轨迹上两点作的速度方向的垂线，垂线交点就是圆心；弦的中垂线和轨迹上某点速度方向垂线相交于圆心.因此，弦对于确定圆心非常关键.

1.3 常见设问

(1)与半径有关的几何问题，半径作为物理模型和几何模型的纽带.分为两种情况：

1)已知物理量(如速度、磁场、比荷等)得半径，求得几何关系；

2)已知几何关系得半径，求得物理量.

弦长与半径和圆心角有关，因此分析此类问题可以从弦入手.

(2)与时间有关的问题.带电粒子在匀强磁场中运动的时间与弧所对应的圆心角有关，在半径一定的情况下，弦长与圆心角有一一对应的关系，因此可以通过弦长确定运动的时间.

2 带电粒子在匀强磁场中运动的模型建构

构建模型是解决问题的常用方法，是培养学生科学思维的重要组成部分，本单元模型构建是将带电粒子的运动过程转化为几何模型，利用几何关系解决问题.不失一般性，作带电粒子在某匀强磁场中运动轨迹模型图，如图1所示.

图1 带电粒子在匀强磁场中做匀速圆周运动的轨迹模型

实线圆弧为带电粒子在磁场中的实际轨迹，为了更方便研究几何关系，特地用虚线将圆周补充完整.聚焦平面几何圆与直线的性质，按从点到线，线到角的思路，确定几何关系和物理内涵.

表1反映了构建模型的思路，含有括号的为物理名词或物理量，通过建模将几何量和物理量一一对应起来.

表1 带电粒子在匀强磁场中做匀速圆周运动的模型建构思路

3 解题思路

大概念教学理念下，以“弦”为分析问题核心和以“半径”为解决问题核心框架.

本单元解决问题的思路是运用与弦的相关几何性质，结合题目所给条件，来确定入射点和射出点，从而确定圆心、半径、轨迹，再求解相应的几何量.根据解题思路，提出了带电粒子在匀强磁场中运动的分析和解决问题框架，如图2所示.框架左侧部分为分析过程，框架右侧部分为求解过程.

图2 以“弦”为分析问题核心和以“半径”为解决问题核心框架

3.1 分析过程

分析过程主要是构建模型，根据题目所给信息，确定弦，从而确定圆心半径.关于如何确定弦，一般有以下两种情况：

(1)已知入射点和射出点位置，两点连线即弦；

(2)已知初、末速度方向和入射点(射出点)，能确定弦，这利用了弦所在直线是初速度方向和末速度方向的角平分线性质.

临界条件和极值条件主要是用于确定末速度方向和射出点位置，从而辅助其他条件确定弦.比如临界条件有恰好不从某条边界出磁场，可以确定临界末速度方向与该条边切线方向一致；极值条件有最远的射出点，或者从哪一点射出时间最长等，在这种情况下，可以利用弦为直径时最长的性质确定最远的点，或者当弦切角最大时，在磁场内运动的时间最长等.

若弦已确定，入射点和射出点、半径、圆心角、轨迹等都能很容易确定了.确定弦的目的主要是为了确定圆心、半径、轨迹，构建带电粒子在匀强磁场中运动的几何模型.

3.2 求解过程

求解过程是建立在以半径为中间量进行的，待运动模型建立后，只需要利用几何关系和半径、周期公式便可以求解设问了.

以弦为核心的分析问题和以半径为核心的解决问题框架，能解决大多数带电粒子在匀强磁场中运动的各种问题，比如临界问题、极值问题、直线边界、圆形边界等.该框架抓住了弦作为几何模型核心以及半径r作为连接几何模型和物理模型的桥梁，容易找到突破口，解题方便快捷.

4 用框架分析典型例题

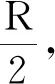
图 3 例1题图

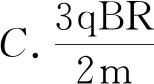
分析：根据例1所给信息，已知入射点位置、入射方向、末速度方向，利用弦所在直线是初速度和末速度方向夹角的角平分线，因此过入射点画一条与初速度方向夹角为30°的直线，与圆形磁场的交点即为射出点，便很容易确定了圆心、半径、轨迹，如图4所示.由几何关系不难得到两圆心和两圆交点构成的四边形为菱形.故答案为选项B.

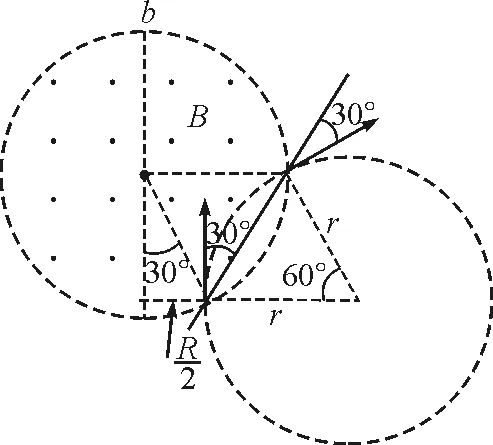
图 4 例1解析图

【例2】(2013年高考海南卷)如图5所示，纸面内有E，F，G3点，∠GEF=30°，∠EFG=135°，空间有一匀强磁场，磁感应强度大小为B，方向垂直于纸面向外.先使带有电荷量为q(q>0)的点电荷a在纸面内垂直于EF从F点射出，其轨迹经过G点；再使带有同样电荷量的点电荷b在纸面内与EF成一定角度从E点射出，其轨迹也经过G点.两点电荷从射出到经过G点所用的时间相同，且经过G点时的速度方向也相同.已知点电荷a的质量为m，轨道半径为R，不计重力，求：

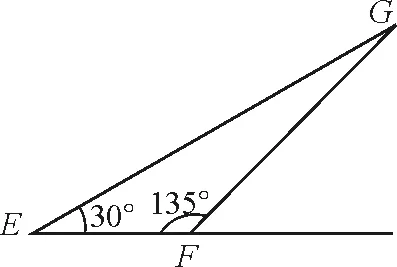
图5 例2题图

(1)点电荷a从射出到经过G点所用的时间；

(2)点电荷b的速度大小.

分析：如图6所示，从F点出发的a经过G点，FG即为弦，且弦切角为45°，因此末速度方向水平向右；根据题目所给条件，b的入射点和射出点分别为E和G，因此线段EG即为b在此过程圆周运动的弦，因为与a末速度方向相同，延长EG，与末速度方向夹角等于弦切角，所以入射速度方向与水平方向夹角为60°，圆心角也为60°，求解过程略.

图6 例2解析图

图7 例3题图

分析：根据题目所给条件，已知入射点和初速度方向，因为速率不同，所以粒子射出磁场位置会分布在ab半圆弧上.由与周期与速率无关，粒子在磁场中运动时间取决于圆心角，根据几何性质，圆心角等于弦切角2倍，所以当弦切角最大时时间最长.过入射点作一条直线相交于半圆，入射点到交点的线段即为轨迹圆周所对应的弦，当该直线与圆周相切时，弦切角最大，如图8所示，根据几何关系，最大圆心角为240°.

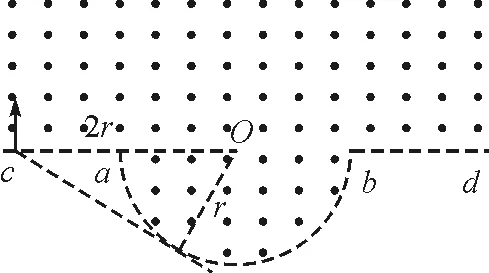
图 8 例3解析图

图9 例4题图

分析：依题意，带电粒子在磁场中做圆周运动的半径为一定值，根据框架的思路，α粒子打在ab板的点为射出点，S点为射入点，两点连线即为弦，因为入射点位置固定，所以当弦为直径时，打在ab板位置最远，在确定了α粒子绕行方向后，便很快能确定A点为右侧最远点，SA为直径，如图10所示.但左侧最远处不是弦为直径时对应的位置，这里要考虑一个实际情况就是，α粒子不能穿过ab板且速度无损失的情况下绕回来，这个极值问题也是一个临界问题，不难想到，当轨迹与ab板相切时，切点B为在左侧最远的点，临界末速度方向确定，半径大小已知，因此可以作一条平行于ab板且间距等于半径大小的辅助线，圆心必定在此辅助线上，就可以确定圆心的位置了，当然此种情况不需要确定弦，我们确定弦最终的目的是需要找到圆心、半径、轨迹.AB段长度即为被α粒子打中的区域的长度.

图10 例4解析图

依据框架分析和解决带电粒子在磁场中做匀速圆周运动的问题，不必归类分析，框架具有高度的概括性，只要抓住“弦”不放手，便能找到突破口.围绕模型构建和该框架进行教学，教学结构明确，思路清晰，更重要的是能培养学生分析和解决问题的关键能力.