范德瓦耳斯气体体积修正的新计算方法*

蓝善权

(岭南师范学院物理科学与技术学院 广东 湛江 524048)

1 引言

1 mol理想气体物态方程为

pVm=RT

(1)

理想气体模型中的气体分子是质点，没有体积.而实际气体分子是有体积的，特别是当气体很稠密时，体积对物态方程的修正是很明显的，它的效果相当于分子间的排斥力.再考虑到分子间的吸引力作用，实际气体物态方程可以更好地近似为范德瓦耳斯方程[1,2]

(2)

式中参数b表征的就是因分子体积而带来的修正值，它由实验测定.此外，也可以从理论上证明参数b的数值约等于1 mol气体所有分子体积总和的4倍[3～5].本文介绍一种新的计算方法求参数b.

2 体积修正的新计算方法

如图1所示，设有两半径为r的全同小球1和小球2相互碰撞，其中小球2固定不动，小球1可以从各个方向撞向小球2，则小球1的质心不可到达的区域如图2虚线所示，该区域的体积是

图1 两小球相互碰撞示意图

图2 碰撞过程中小球的有效体积示意图

(3)

设想有1 mol气体在体积为Vm的容器中，现在要计算这NA个气体分子的有效活动空间Vm-b，即计算参数b的值.首先，对NA个气体分子进行编号，令第1个分子为质点，其他分子都“冻结”在一定的位置上，在分子1和其他分子碰撞的过程中，其他分子小球的有效半径为d，如图2虚线所示.则对于第1个分子，它的不可活动空间是(NA-1)V0.然后，令第1，2个分子为质点，在分子2和其他分子碰撞的过程中，其他有效半径为d的分子球都处于“冻结”状态.则对于第2个分子，它的不可活动空间是(NA-2)V0.接着，令第1，2，3个分子为质点，在分子3和其他分子碰撞的过程中，其他有效半径为d的分子球都处于“冻结”状态.则对于第3个分子，它的不可活动空间是(NA-3)V0.以此类推，可得对于第NA个分子，它的不可活动空间

(NA-NA)V0=0

对所有NA个分子来说，总的不可活动空间是

V=[(NA-1)+(NA-2)+(NA-3)+

(4)

因此，对任意一个分子，平均的不可活动空间(即参数b的值)为

(5)

为什么在计算第2个分子的不可活动空间时，要把第1个分子当成质点？因为第1，2个分子之间的相互碰撞，已经在计算第1个分子的不可活动空间时考虑了，不能重复计算碰撞事件，以此类推，在计算后面分子的不可活动空间时，需要把前面的分子当成质点.

3 总结和讨论

采用新方法，通过考察每一对分子的相互碰撞，计算得到了因分子体积不能忽略而给系统带来的有效体积的修正，结果与其他方法得到的结果一致.下面简要介绍参考文献中的计算方法，并与本文的新方法进行比较.

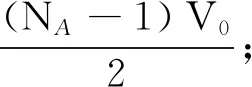
参考文献[4]中参数b的数值为

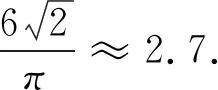
参考文献[5]介绍了由临界点的参数来表示参数b，对氦气的参数b给出了5种表达式和相应的数值，有些数值与4倍所有分子体积总和近似，而有一个数值偏差较大.