基于极值理论的碳价格波动风险管理研究

王喜平，闫丽娜

（华北电力大学 经济管理学院，河北 保定 071003）

0 引言

减少温室气体排放，尽早实现“碳达峰”“碳中和”已成为全球共识。碳交易作为一种可以有效控制温室气体排放的市场调节手段，已成为我国落实减排承诺、实现减排目标的重要政策工具。自2011 年，国内多个省、市开展了碳交易试点。从试点市场的运行结果看，减排效应日渐显现：截至2020 年底，全国8 个碳交易试点单位累计完成成交量超过4 亿吨，累计成交额超过90 亿元，单位GDP（gross domestic product）二氧化碳排放较2005 年降低约48.4%，提前超额完成下降40%～45%的目标[1]。由于受气候、政策、能源价格以及供需机制等多种因素的影响，市场碳交易价格波动剧烈。目前，我国碳市场存在着发展时间短、政策框架不完善、金融化程度不足、碳市场作用发挥不充分等问题，这些问题造成碳市场的交易价格波动存在不确定性[2]；因此，有必要对碳价格波动风险进行研究，以有效避免碳价格风险爆发对碳市场运行带来不利影响。

近年，碳市场价格波动及风险测度成为学界关注的焦点。对于碳价格的波动，多数学者都通过建立GARCH 族模型来进行分析，并得到结论：碳价格具有尖峰厚尾、波动性聚集等特征[3-6]。有学者从碳价的影响因素入手，探讨其对碳价波动的作用。文献[7]利用向量误差修正模型对核证减排量现货价格进行了分析，认为宏观因素和气候因素对碳价影响最为显著。文献[8-13]分别运用GARCH 模型、向量自回归模型、多尺度熵等方法研究了能源价格与碳排放权价格之间的关系，认为碳价格主要受天然气、石油价格的影响。

在此基础上，诸多学者利用不同的方法对碳价收益率的在险价值进行了度量。文献[14]运用极值理论，对欧盟碳排放权交易的现货市场和期货市场风险进行了测度，认为运用极值理论估计VaR 比传统方法更加有效。文献[15]将经验模态分解算法和ARMA-EGARCH 结合，构建了多时间尺度的VaR 模型；结果表明用该方法能够有效降低极端事件的影响，获得更为准确的碳市场风险值。文献[16]用经济状态依赖方法估计欧盟碳市场的风险，认为该方法在样本外VaR 预测中的结果优于传统方法结果。

以上研究主要围绕欧盟碳市场展开。对于我国碳交易试点市场的风险测度，文献[17]对我国碳试点碳价收益率构建 ARCH（autoregressive conditional heteroscedasticity）族模型并计算了各交易试点的风险价值VaR，结果显示：不同区域的碳排放交易市场，其波动程度不尽相同，计算的 VaR 有效性也有较大差异。文献[18]利用GARCH（generalized autoregressive conditional heteroscedasticity）模型估计和预测北京碳市场的交易价格，认为模型在95%的置信水平下能够准确度量碳价风险。文献[19]认为QAR-GARCH（quantile autoregression-generalized autoregressive conditional heteroscedasticity）模型比 CAVaR（conditional autoregressive value at risk）族模型更加适用于对我国碳市场风险的测度。

我国在碳交易方面刚刚起步，存在数据量小的问题；所以，关于这方面的研究主要集中在碳价格的影响因素、碳价格波动特征等方面。在为数不多的对我国碳价风险的研究中，尚未发现有文献将极值理论运用到风险价值度量中。极值理论更注重对尾部风险的刻画，提供了一种更加准确的VaR 估计方法。目前，极值理论估计VaR 已经被广泛应用于金融、保险、原油市场的风险度量中，并且都得到了较为准确的估计结果[20-23]。碳价收益率的波动也具有明显的厚尾特征，受极端事件的影响较大。我国从2013 年建立碳交易试点至今，交易时间已有8 年，交易价格和交易量的相关数据也有了一定的积累，所以可以以此为基础来尝试碳价收益率波动风险方面的研究。

鉴于此，本文在借鉴已有研究的基础上，以碳交易试点市场——深圳相关数据为研究背景，将条件方差和极值理论结合，度量我国碳价收益率的波动风险，为碳价波动风险管理提供参考借鉴。

1 模型构建及原理

1.1 VaR

在金融市场中，在险价值VaR 被广泛应用于对市场风险的衡量。它是指在一定的置信度和给定的时间期间内，由于价格变化引起的超过目标水平的最大损失。该指标最大的优点在于，可用单一的数值对一定时间间隔内的风险进行总结。对任一收益率序列的分布函数F(X)，当置信水平为p时，如果用V表示该序列VaR，则有：

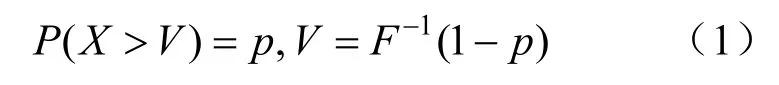
ES（expected shortfall）是指当投资组合的损失超过VaR 时所遭受的平均损失程度。VaR 难以有效反映序列尾部的小概率事件发生时的情况，而ES 很好地弥补了这一不足。

若将ES 用E表示，那么该收益率序列的ES可表示为：

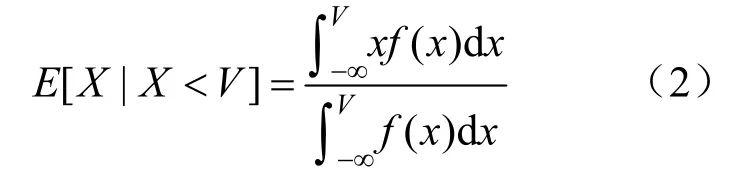
1.2 ARMA-GARCH

以往的研究显示，我国碳价收益率存在明显的波动聚集性和异方差性；因此，可以用ARMA(p,q)-GARCH(m,n)来捕捉其波动特征。

ARMA 模型通常用来描述价格变化的历史规律，AR(p)为自回归部分，MA(q)为移动平均过程。

GARCH 模型又称为异方差模型，它由ARCH模型演化而来，用于描述时间序列的异方差性。GARCH 模型由均值方程和条件方差方程进行刻画。

将ARMA 过程加入到GARCH 模型的均值方程中，以更好地挖掘时间序列的残差信息，使得残差序列更加服从独立同分布的假设，从而更好地刻画时间序列的波动性。模型的具体表达式如下：

式中：均值方程中，rt表示碳价格的对数收益率；εt表示残差。条件方差方程中，为残差εt的条件方差；It–1表示t时刻以前所有信息集；ηt表示均值为0、方差为1 的独立同分布时间序列。

1.3 极值理论

金融时间序列往往具有肥尾分布的特征，通常不满足正态分布的假定。根据极值理论，x值超过临界值μ时的累积分布函数为：

这种分布被称为 GPD（generalized pareto distribution），其中：y=(x-μ)/β，β>0，β为比例参数；ξ为形状参数；Nμ表示序列中超过临界值μ的数目；N为总体数目。

在极值理论中，衡量尾部风险有2 种常见的模型：一种是超越阈值的极值模型POT（peak over threshold）；另一种为区间选取极值模型BMM（block maxima group of models），这种模型更适合对具有一定周期性或季节性的数据进行建模。

考虑到本文所研究的碳市场相关数据背景中，碳价收益率的波动不存在随季节变化的特征；因此，本文更适合采用POT 对序列尾部进行建模。

经过推导分别得到VaR 和ES 的求解公式：

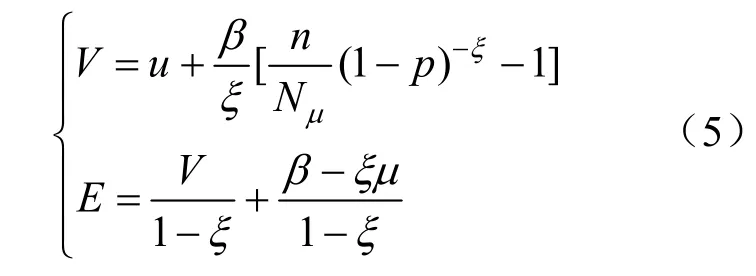
用POT 模型计算VaR 时，首先要通过GPD分布对极值数据进行拟合，其次可通过图像观察安全阈值。一般通过平均超额函数图法和Hill 图法来确定阈值μ。

1.3.1 平均超额函数图法

利用平均超额函数图作为确定阈值μ的依据。定义随机变量X超过阈值的平均超额值e(μ)：

由于GPD 的平均超额函数是阈值的线性函数，所以可以通过寻找超过某一观测值后图像趋于线性的这一点来确定阈值μ。

1.3.2 Hill 图法

另一个可以确定阈值的工具是Hill 图法。定义Hill 统计量Hk：

式中：k为样本容量，k=1,2,···,n–1,n；次序统计量X(i)满足X(i)>X(i–1)。

用k表示横坐标轴，绘制Hk的函数图像；选取图像中Hk趋于稳定时所对应的k，将X(k)确定为阈值μ。

由于上述2 种方法均是通过观察图像来确定阈值，故存在一定的主观性。DuMouchel（1983）提出的一个较为简单的量化方法：认为应该选取序列中超过临界值μ的数目占总体样本的90%时所对应的μ作为阈值。本文将结合平均超额函数图法与Hill 图法，并以90%时所对应的阈值作为参考共同确定最优的阈值μ。

1.4 动态VaR 及回测检验

VaR 的测度分为静态和动态2 种方法。前文给出了静态VaR 的计算公式。静态VaR 值相对更加直观。在预测收益率风险的时候，动态VaR 会与收益率序列同时发生波动，这样可以更好地拟合序列的波动性。用Vt表示动态的VaR，则其计算公式为：

最后，需要对VaR 的有效性和准确性进行检验。常用的检验方法是Kupiec 回测检验。基于伯努利分布构造LR 统计量，用L表示LR 统计量，则有：

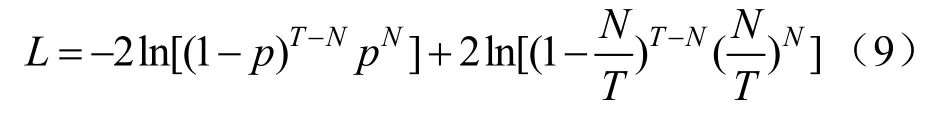
式中：N为失败的时长；T为实际考察的时长；N/T为失败率；p为给定的置信水平。该假设检验的原假设为：p=N/T。

可通过观察实际的失败率与估计的失败率是否相近，来确定模型的优劣。如果原假设成立，则认为似然估计量LR 近似服从自由度为1 的卡方分布。因此，当置信水平给定时，就可以通过LR 的值判断是否拒绝原假设。

2 实例分析

深圳碳交易试点是全国首个正式运行的交易试点。试点交易品种包括SZA-2013、SZA-2014等。交易主体主要为交易所内规定的管控单位、其他机构投资者和个人投资者，涉及电力、制造业、燃气等多个行业。

自深圳碳试点成立以来，碳价格发生了较大幅度的变化。图1 显示了深圳碳配额成交均价。从图中可以看出，深圳碳交易试点成立之初，交易价格偏高；这可能是由于碳市场起步阶段受到国家政策的积极引导，激发了投资者参与碳市场交易的热情。2015—2017 年，价格逐渐趋于平稳波动的状态，并且表现出明显的周期性变化趋势。2018—2019 年间，价格一度陷入低迷。

图1 2013—2019 年深圳碳配额成交均价走势图Fig.1 Trend chart of average transaction price of carbon quota in Shenzhen from 2013 to 2019

2.1 数据来源

本文选取了2013 年12 月26 日至2020 年10月9 日的日度交易数据。深圳碳交易产品种类较多，按交易量加权平均后得到平均交易价格，然后去除交易量为0 的数据后，得到共计1 824 个数据。为了满足数据的平稳性要求，将碳交易价格取对数收益率，则第t个交易日的碳价格收益率rt可表示为：

数据经处理后，得到图2。由图2 可见，碳价收益率均值为–0.000 477，方差为0.267 706，偏度为0.200 868，峰度为14.052 70。正的偏度值表明碳价收益率序列存在右偏概率分布性质；较大的峰度值表明碳价收益率序列存在尖峰厚尾的特征。JB 统计量为9 291.448，该结果显然拒绝了收益率序列服从正态分布的假设。

图2 深圳碳价收益率的描述性检验结果Fig.2 Descriptive test results of Shenzhen carbon price yield

2.2 ARMA-GARCH 模型的选择

2.2.1 序列的平稳性检验

首先，需要对碳价收益率序列进行平稳性检验。根据表1 中收益率序列平稳性检验结果可知，深圳碳价格收益率序列的T 统计量小于99%置信度时对应的临界值，因此拒绝序列存在单位根的假设，故认为序列是平稳的。

表1 收益率序列的平稳性检验结果Tab.1 Stationarity test results of the rate of return series

2.2.2 ARMA-GARCH 模型阶数的确定

在收益率平稳的基础上，需要对碳价收益率序列的自相关性进行拟合。大量关于风险度量的研究发现，一阶或二阶的ARMA-GARCH 模型能够较为充分地刻画时间序列的特征。结合AIC（akaike information criterion）和SC（schwarz criterion）原则，可以基本确定最优模型。通过比较拟合结果，在系数均显著的条件下，认为ARMA（2,0）模型能够更加充分地捕捉深圳碳价收益率的自相关特征。

对模型拟合后的残差序列进行ARCH 效应检验，检验结果如表2 所示。序列在99%的置信度下拒绝原假设，认为序列确实存在ARCH 效应。因此，需要进一步引入GARCH 模型。

表2 残差序列的ARCH 效应检验结果Tab.2 ARCH effect test results of residual series

表3 示出了不同阶数下ARMA-GARCH 模型的拟合结果。通过对比AIC 和SC 的值，发现最好的拟合模型是ARMA(2,0)-GARCH(1,1)模型。

表3 不同阶数ARMA-GARCH 模型拟合结果Tab.3 Fitting results of ARMA-GARCH models with different orders

表4 示出了ARMA(2,0)-GARCH(1,1)模型的拟合结果。从表4 的估计结果可以看出，AR(1)和AR(2)的系数均通过了显著性检验，说明深圳碳价收益率序列存在自相关性。ARCH(1)和GARCH(1)系数均显著且大于零，满足系数和小于1 的条件。系数和为0.99，接近于1，表明收益率序列存在波动性集聚的现象，即：前一时期的收益率波动会影响下一期的收益率波动。当市场受到冲击时，波动虽然会逐渐减弱，但持续时间较长。另外，由于ARCH 项的系数明显小于GARCH项系数，说明收益率波动受到自身记忆性的影响要强于市场冲击所带来的影响。

表4 ARMA(2,0)-GARCH(1,1)模型的拟合结果Tab.4 Fitting results of ARMA(2,0)-GARCH(1,1) model

对ARMA(2,0)-GARCH(1,1)模型拟合的残差序列进行ARCH-LM 检验，结果如表5 所示。从表5 可以看出，F 统计量的p值为0.1586，明显大于0.05 的显著性水平。因此，可以认为ARMA(2,0)-GARCH(1,1)基本消除了碳价收益率序列的异方差性。根据估计结果可以得到ARMA(2,0)-GARCH(1,1)模型的表达式为：

表5 残差项的ARCH-LM 检验结果Tab.5 ARCH-LM test results of residuals

2.3 标准残差序列的GPD 拟合

本文通过R 语言的evir 工具包，运用极值理论中的POT 模型对ARMA(2,0)-GARCH(1,1)模型得到的标准残差序列进行GDP 分布的拟合。由于POT 模型拟合时需要数据均为正值，本文将深圳碳价收益率的标准残差序列分为正、负2 部分，分别进行拟合。对于残差正序列，首先通过绘制平均超额函数图和Hill 图确定合适的阈值。通过观察图3可以看到：平均超额函数在2 之后，数据变得稀松；在1.5～2 之间存在一定的线性关系。因此，可以初步判定阈值应该大于1.5。结合图4 中Hill 图可以看出，图像在残差序列的第76 个之后逐渐平稳，对应的阈值在应小于1.9。另外根据DuMouchel 提出的量化方法，认为超出阈值的数目应该小于10%。因此，最终确定的阈值为1.811 015。

图3 上尾的平均超额函数图Fig.3 Average excess function of the upper tail

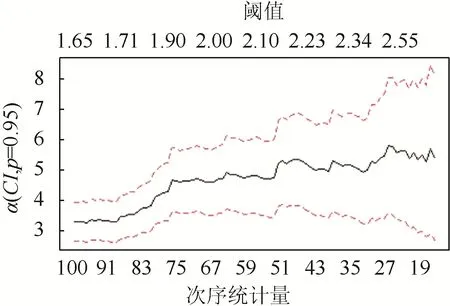
图4 上尾的Hill 图Fig.4 Hill of the upper tail

在确定合适的阈值后，利用极大似然估计得到残差序列尾部拟合GPD 分布的参数ξ值为0.004 850 581，β值为0.608 867 825。

由绘制出的图5 超额分布和和图6 拟合的GPD 分布，可以看出GPD 曲线对数据进行了非常好的拟合。

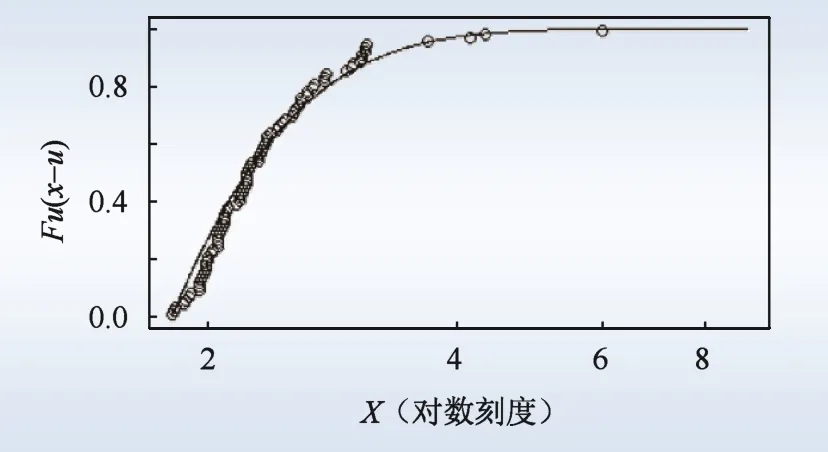
图5 上尾的超值分布图Fig.5 Premium distribution chart of the upper tail

图6 上尾的内在分布尾部图Fig.6 Intrinsic distribution of the upper tail

在图7 上尾的残差散点图和图8 的残差Q-Q图中，残差均匀散落，极少数点没有落在直线上，基本满足GPD 分布的假设条件。可见，标准残差上尾对GPD 分布的拟合程度较好。

图7 上尾的残差散点图Fig.7 Residual scatter plot of the upper tail

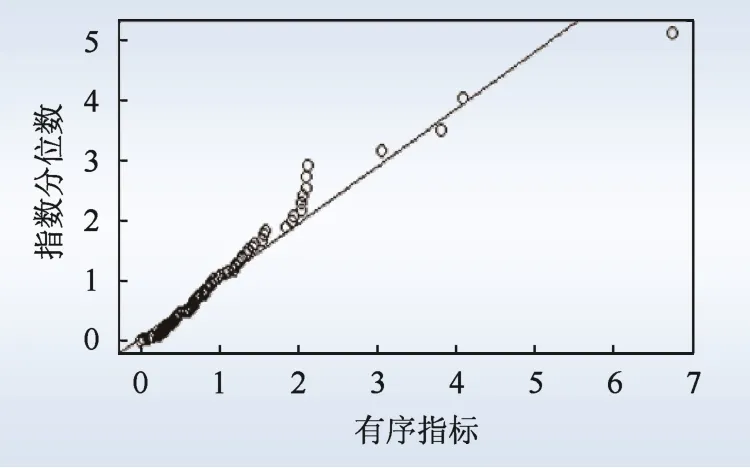
图8 上尾的残差Q-Q 图Fig.8 The residual Q-Q plot of the upper tail

根据静态VaR 的计算公式计算结果可以得到：在99%的置信水平下，深圳碳价收益率的上尾静态VaR 值为 3.214 282；这意味着有99%的可能性，由市场价格变化带来的碳价收益率变化不会超过3.214 282。ES 值为 3.832 957，99%的分位数为3.214 282；这意味着如果3.214 282 的收益率被超过了，则预期损失为3.832 957。

图9 示出了99%置信水平下的VAR 与ES。第一条垂直虚线和对应的轮廓似然曲线显示了估计的VaR，第二条垂直虚直线和对应的轮廓似然虚线显示了估计的ES。图中，轮廓似然虚线与水平虚直线的2 个交点分别是估计出的置信区间边界。

图9 上尾99%的VaR 与ES 估计Fig.9 VaR and ES estimation at 99%confidence level of the upper tail

用同样的方法对负的标准残差序列进行GPD尾部拟合，结果如图10 所示。从图10 可以看出，平均超额函数图中横坐标值大于2 之后，数据变得稀松，在1.5～2 之间存在一定的线性关系：由此可以初步判定阈值应该大于1.5。结合图11 中的Hill 图可以看出，图像曲线在残差序列第86 个之后逐渐平稳，对应的阈值应小于1.8，最终确定的阈值为–1.611 475。通过极大似然估计，得到参数ξ=0.008 154 222，β=0.525 983 924。从输出图12 可以看出，下尾收益率序列的拟合效果也比较好。根据静态VaR 的计算公式，可以得到：碳价收益率的下尾静态VaR 值为–2.826 280；这表明有99%的可能性，由市场价格变化带来的碳价收益率变化不会低于–2.826 280。ES 值为3.366 575，99%的分位数为–2.826 280；这表示如果超过了–2.826 280 的收益率，则预期损失为–3.366 575。

图10 下尾的平均超额函数Fig.10 Average excess function of the lower tail

图11 下尾的Hill 图Fig.11 Hill of the lower tail

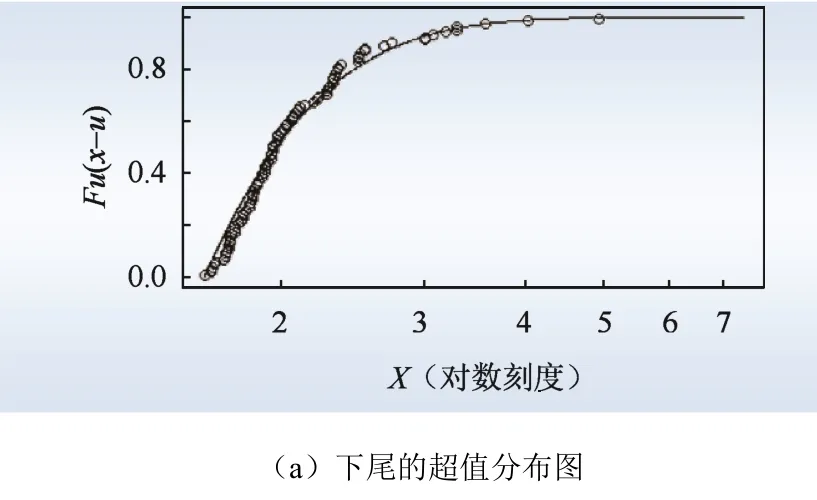
图12 下尾的分布输出值Fig.12 Distribution output of the lower tail

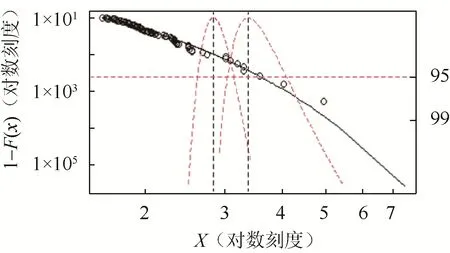
图13 示出了99%置信水平下下尾的VaR 与ESFig.13 VaR and ES estimation at 99% confidence level of the lower tail

3 回测检验

由于动态VaR 可以更好地拟合收益率的波动性，因此将ARMA(2,0)-GARCH(1,1)得到的残差序列的条件均值和条件方差代入动态VaR 的计算公式，可以得到动态VaR 序列。

图14 为上涨的动态VaR，图15 为下跌的动态VaR。无论是上涨还是下跌，动态VaR 都很好地包络了收益率曲线。在VaR 的回测检验中发现：在上涨的动态VaR 中，共有847 个观测值，VaR失效的个数共有4 个，失败率为0.004 72；下跌的动态VaR 中，共有974 个观测值，VaR 失效的个数共有9 个，失败率为0.009 24。

图14 上尾的动态VaR 与收益率Fig.14 Dynamic VaR and rate of return of the upper tail

图15 下尾的动态VaR 与收益率Fig.15 Dynamic VaR and rate of return of the lower tail

通过计算99%置信水平下的LR 统计量，得到上涨的LR 值为1.286 336，下跌的LR 值为0.025 306，均小于99%置信水平下的临界值6.635：因此，认为该模型对深圳碳价收益率VaR的估计是有效的。

4 结论

本文以碳排放权交易价格为研究对象，在考虑了极端情况碳价波动风险的条件下，将条件方差和极值理论结合起来，对碳价收益率进行了建模。对比结果显示，ARMA-GARCH-EVT 模型能够更加准确地衡量极端条件下的碳价波动风险。回测检验结果表明，模型的检验失败率较低，所以认为模型在99%的置信水平下是有效的。

从得到的VaR 估计结果来看，深圳碳市场的价格波动较大，虽然下尾的静态VaR 值小于上尾的静态VaR 值，但下尾的动态VaR 值在2019 年4 月达到–3.216 51。当投资者面临这种风险时，会遭受巨大的损失，引起整个碳市场的波动。因此，建议对碳市场进行必要的风险管控。政府应在稳定碳价方面发挥重要作用，建立相应的市场稳定储备机制。金融机构也应积极参与碳市场建设，为碳市场设计更加多样的风险控制工具，从而帮助控排企业更好地管理风险。